In this article, Youssef LOURAOUI (Bayes Business School, MSc. Energy, Trade & Finance, 2021-2022) presents the long-short equity strategy, one of pioneer strategies in the hedge fund industry. The goal of the long-short equity investment strategy is to buy undervalued stocks and sell short overvalued ones.
This article is structured as follow: we introduce the long-short strategy principle. Then, we present a practical case study to grasp the overall methodology of this strategy. We conclude with a performance analysis of this strategy in comparison with a global benchmark (MSCI All World Index).
Introduction
According to Credit Suisse, a long-short strategy can be defined as follows: “Long-short equity funds invest on both long and short sides of equity markets, generally focusing on diversifying or hedging across particular sectors, regions, or market capitalizations. Managers have the flexibility to shift from value to growth; small to medium to large capitalization stocks; and net long to net short. Managers can also trade equity futures and options as well as equity related securities and debt or build portfolios that are more concentrated than traditional long-only equity funds.”
This strategy has the particularity of potentially generate returns in both rising and falling markets. However, stock selection is key concern, and the stock picking ability of the fund manager is what makes this strategy profitable (or not!). The trade-off of this approach is to reduce market risk but exchange it for specific risk. Another key characteristic of this type of strategy is that overall, funds relying on long-short are net long in their trading exposure (long bias).
Equity strategies
In the equity universe, we can separate long-short equity strategies into discretionary long-short equity, dedicated short bias, and quantitative.
Discretionary long-short
Discretionary long-short equity managers typically decide whether to buy or sell stocks based on a basic review of the value of each firm, which includes evaluating its growth prospects and comparing its profitability to its valuation. By visiting managers and firms, these fund managers also evaluate the management of the company. Additionally, they investigate the accounting figures to judge their accuracy and predict future cash flows. Equity long-short managers typically predict on particular companies, but they can also express opinions on entire industries.
Value investors, a subset of equity managers, concentrate on acquiring undervalued companies and holding these stocks for the long run. A good illustration of a value investor is Warren Buffett. Since companies only become inexpensive when other investors stop investing in them, putting this trading approach into practice frequently entails being a contrarian (buy assets after a price decrease). Because of this, cheap stocks are frequently out of favour or purchased while others are in a panic. Traders claim that deviating from the standard is more difficult than it seems.
Dedicated short bias
Like equity long-short managers, dedicated short bias is a trading technique that focuses on identifying companies to sell short. Making a prediction that the share price will decline is known as short selling. Similar to how purchasing stock entails profiting if the price increases, holding a short position entail profiting if the price decreases. Dedicated short-bias managers search for companies that are declining. Since dedicated short-bias managers are working against the prevailing uptrend in markets since stocks rise more frequently than they fall (this is known as the equity risk premium), they make up a very small proportion of hedge funds.
Most hedge funds in general, as well as almost all equity long-short hedge funds and dedicated short-bias hedge funds, engage in discretionary trading, which refers to the trader’s ability to decide whether to buy or sell based on his or her judgement and an evaluation of the market based on past performance, various types of information, intuition, and other factors.
Quantitative
The quantitative investment might be seen as an alternative to this traditional style of trading. Quants create systems that methodically carry out the stated definitions of their trading rules. They use complex processing of ideas that are difficult to analyse using non-quantitative methods to gain a slight advantage on each of the numerous tiny, diversified trades. To accomplish this, they combine a wealth of data with tools and insights from a variety of fields, including economics, finance, statistics, mathematics, computer science, and engineering, to identify relationships that market participants may not have immediately fully incorporated in the price. Quantitative traders use computer systems that use these relationships to generate trading signals, optimise portfolios considering trading expenses, and execute trades using automated systems that send hundreds of orders every few seconds. In other words, data is fed into computers that execute various programmes under the supervision of humans to conduct trading (Pedersen, 2015).
Example of a long-short equity strategy
The purpose of employing a long-short strategy is to profit in both bullish and bearish markets. To measure the profitability of this strategy, we implemented a long-short strategy from the beginning of January 2022 to June 2022. In this time range, we are long Exxon Mobile stock and short Tesla. The data are extracted from the Bloomberg terminal. The strategy of going long Exxon Mobile and short Tesla is purely educational. This strategy’s basic idea is to profit from rising oil prices (leading to a price increase for Exxon Mobile) and rising interest rates (leading to a price decrease for Tesla). Over the same period, the S&P 500 index has dropped 23%, while the Nasdaq Composite has lost more than 30%. The Nasdaq Composite is dominated by rapidly developing technology companies that are especially vulnerable to rising interest rates.
Overall, the market’s net exposure is zero because we are 100% long Exxon Mobile and 100% short Tesla stock. This strategy succeeded to earn significant returns in both the long and short legs of the trade over a six-month timeframe. It yielded a 99.5 percent return, with a 36.8 percent gain in the value of the Exxon Mobile shares and a 62.8 percent return on the short Tesla position. Figure 1 shows the overall performance of each equity across time.
Figure 1. Long-short equity strategy performance over time
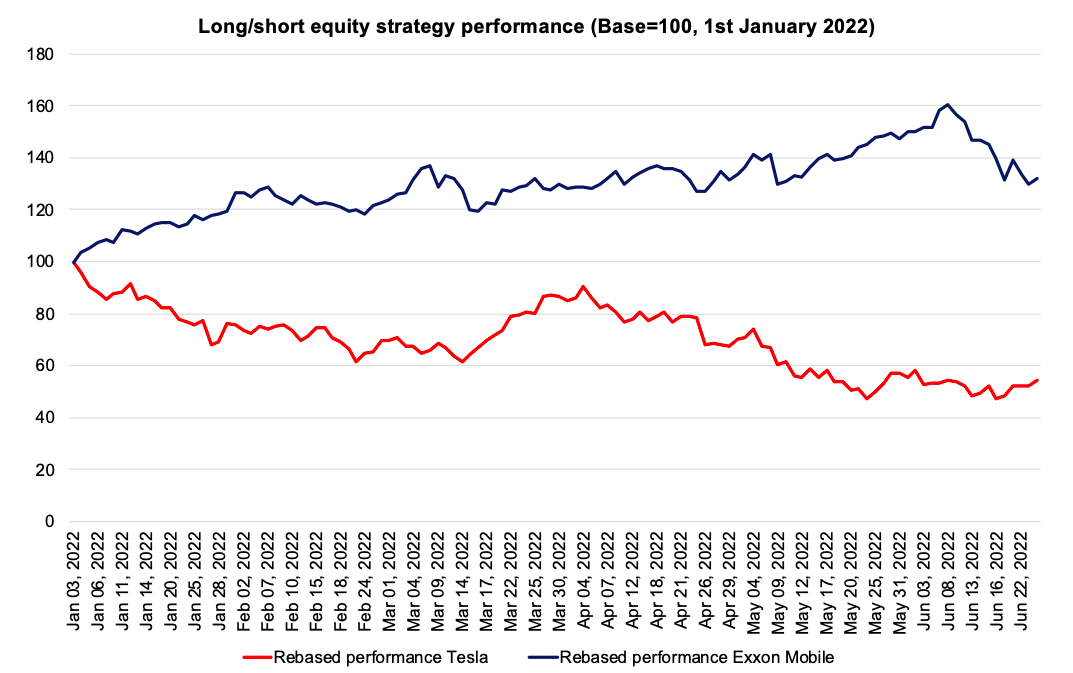
Source: computation by the author (Data: Bloomberg)
You can find below the Excel spreadsheet that complements the example above.
Performance of the long-short equity strategy
To capture the performance of the long-short equity strategy, we use the Credit Suisse hedge fund strategy index. To establish a comparison between the performance of the global equity market and the long-short hedge fund strategy, we examine the rebased performance of the Credit Suisse index with respect to the MSCI All-World Index. Over a period from 2002 to 2022, the long-short equity strategy index managed to generate an annualised return of 5.96% with an annualised volatility of 7.33%, leading to a Sharpe ratio of 0.18. Over the same period, the MSCI All World Index managed to generate an annualised return of 6.00% with an annualised volatility of 15.71%, leading to a Sharpe ratio of 0.11. The low correlation of the long-short equity strategy with the MSCI All World Index is equal to 0.09, which is closed to zero. Overall, the Credit Suisse hedge fund strategy index performed somewhat slightly worse than the MSCI All World Index, but presented a much lower volatility leading to a higher Sharpe ratio (0.18 vs 0.11).
Figure 2. Performance of the long-short equity strategy compared to the MSCI All-World Index across time.
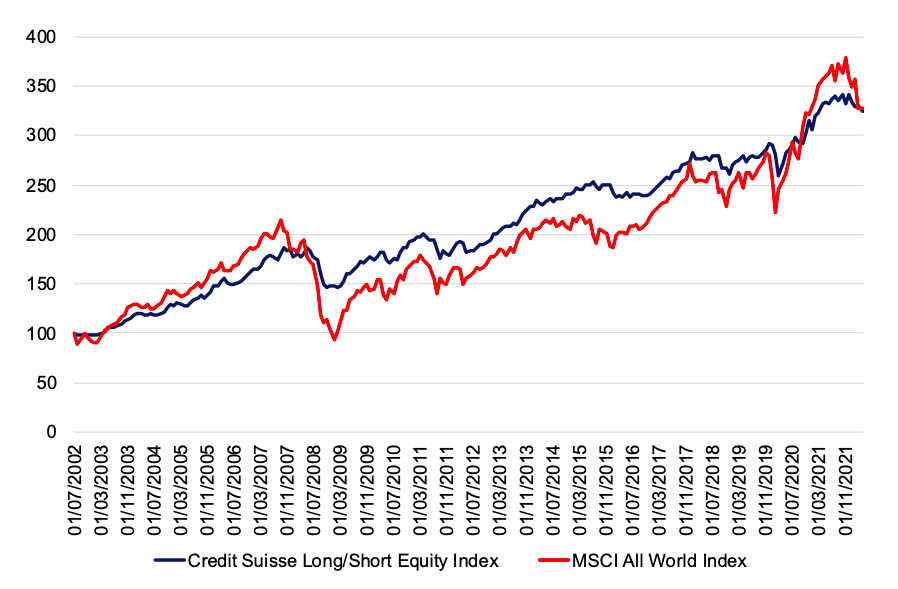
Source: computation by the author (Data: Bloomberg)
You can find below the Excel spreadsheet that complements the explanations about the Credit Suisse hedge fund strategy index.
Why should I be interested in this post?
Long-short funds seek to reduce negative risk while increasing market upside. They might, for example, invest in inexpensive stocks that the fund managers believe will rise in price while simultaneously shorting overvalued stocks to cut losses. Other strategies used by long-short funds to lessen market volatility include leverage and derivatives. Understanding the profits and risks of such a strategy might assist investors in incorporating this hedge fund strategy into their portfolio allocation.
Related posts on the SimTrade blog
▶ Youssef LOURAOUI Introduction to Hedge Funds
▶ Youssef LOURAOUI Portfolio
Useful resources
Academic research
Pedersen, L. H., 2015. Efficiently Inefficient: How Smart Money Invests and Market Prices Are Determined. Princeton University Press.
Business Analysis
BlackRock Long-short strategy
BlackRock Investment Outlook
Credit Suisse Hedge fund strategy
Credit Suisse Hedge fund performance
Credit Suisse Long-short strategy
Credit Suisse Long-short performance benchmark
About the author
The article was written in December 2022 by Youssef LOURAOUI (Bayes Business School, MSc. Energy, Trade & Finance, 2021-2022).



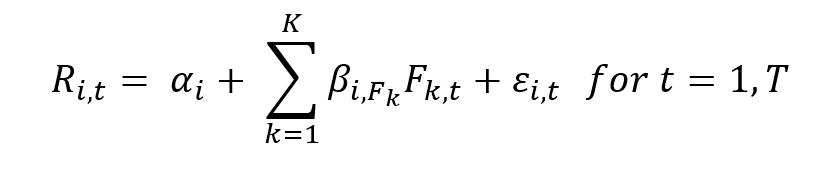
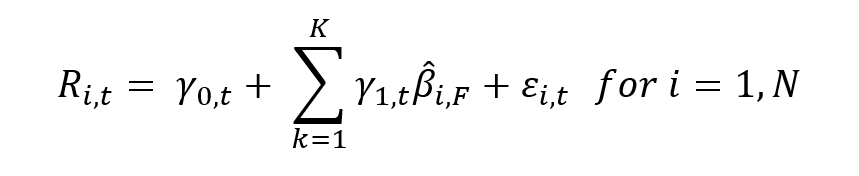
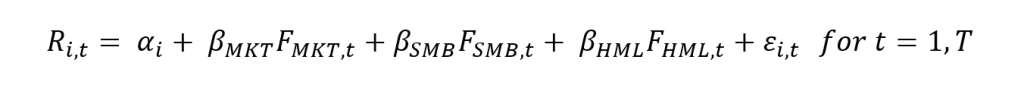
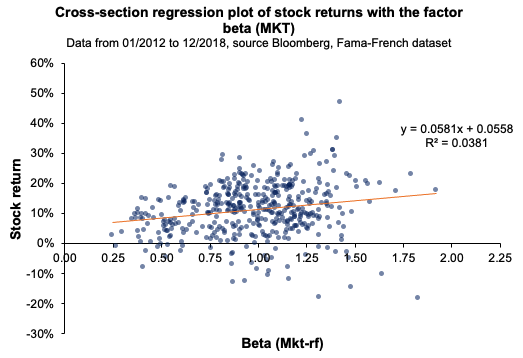 Source: computation by the author.
Source: computation by the author.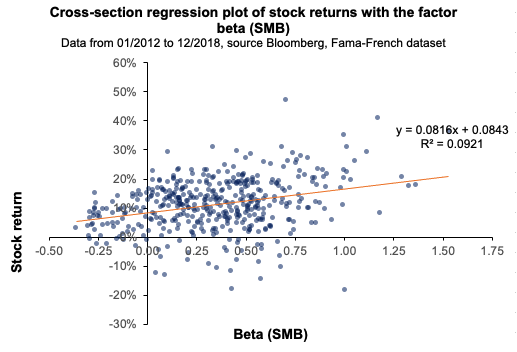 Source: computation by the author.
Source: computation by the author.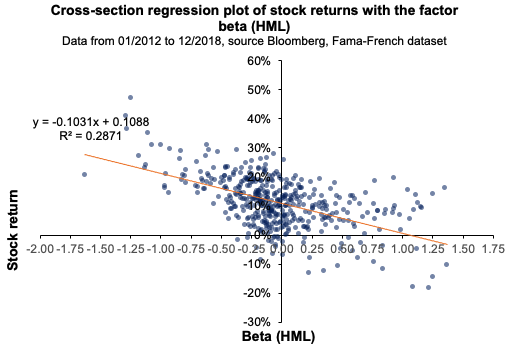 Source: computation by the author.
Source: computation by the author. Source: computation by the author.
Source: computation by the author. Source: computation by the author.
Source: computation by the author. Source: computation by the author.
Source: computation by the author.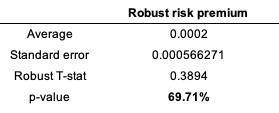 Source: computation by the author.
Source: computation by the author.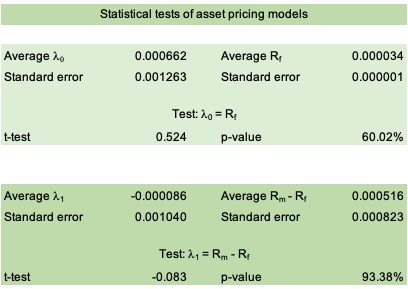 Source: computation by the author.
Source: computation by the author.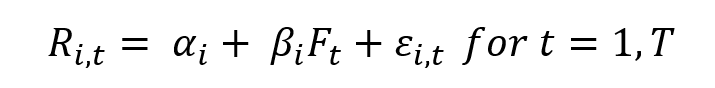
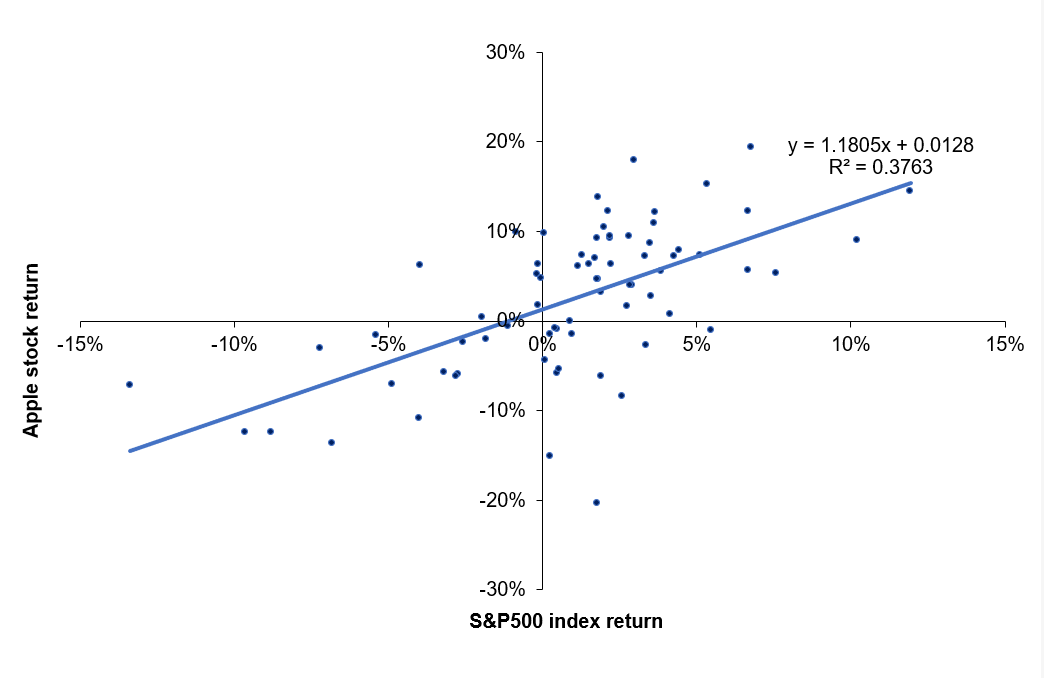 Source: computation by the author.
Source: computation by the author.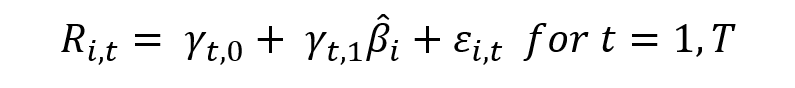
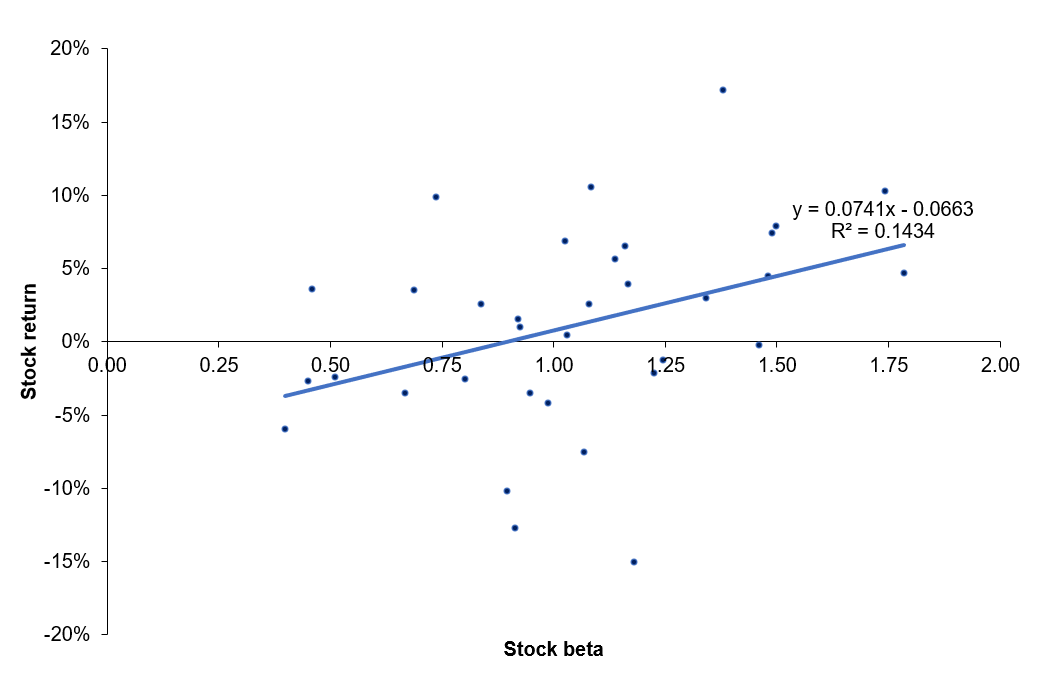


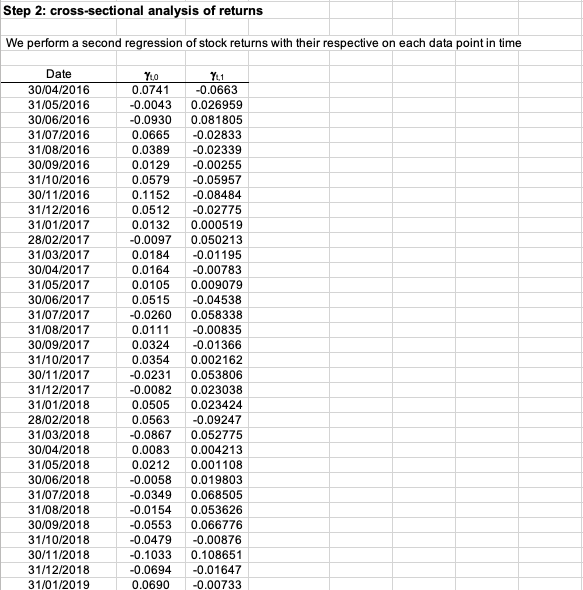


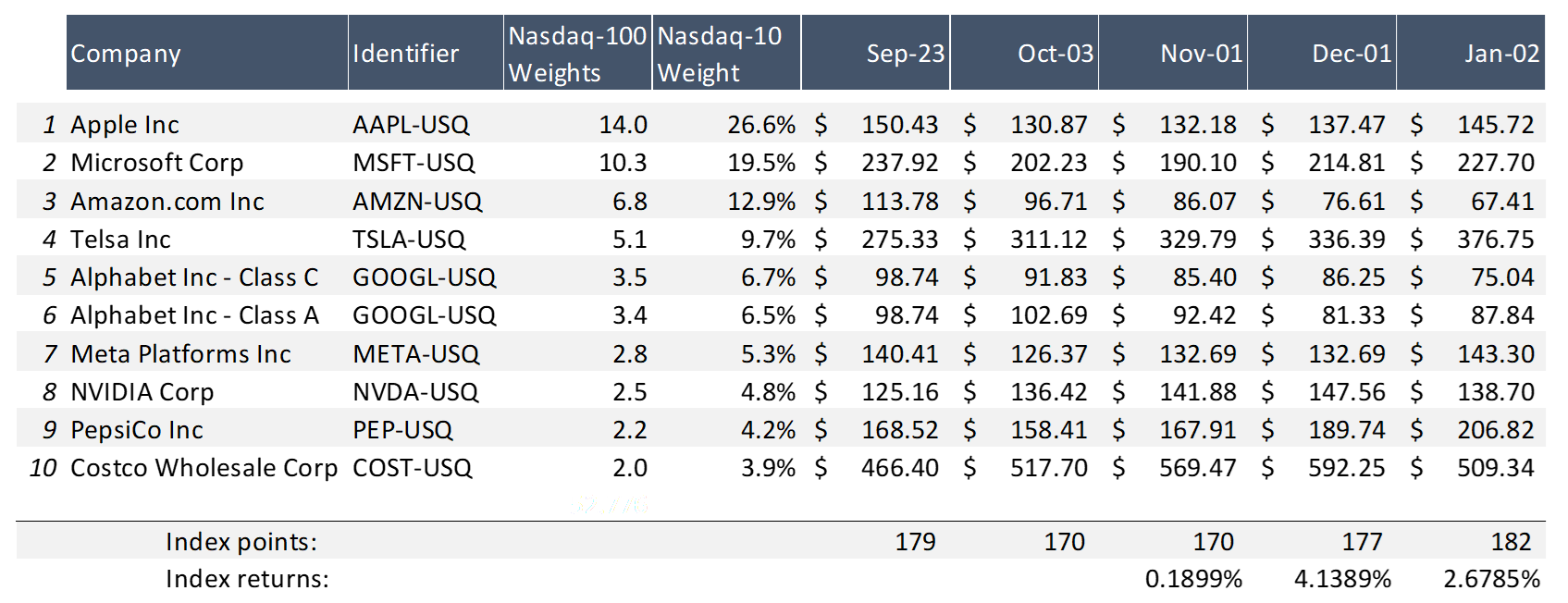



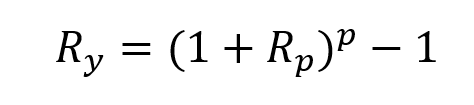
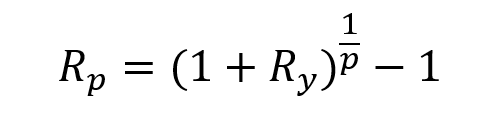




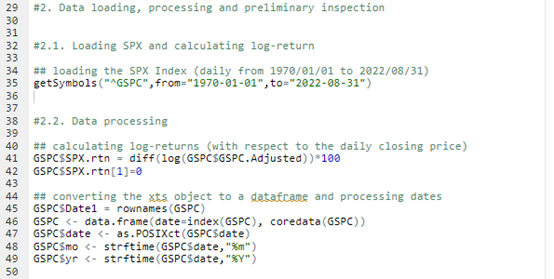
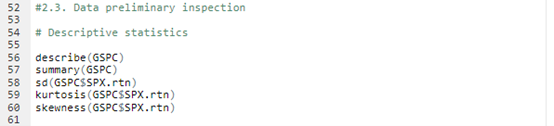
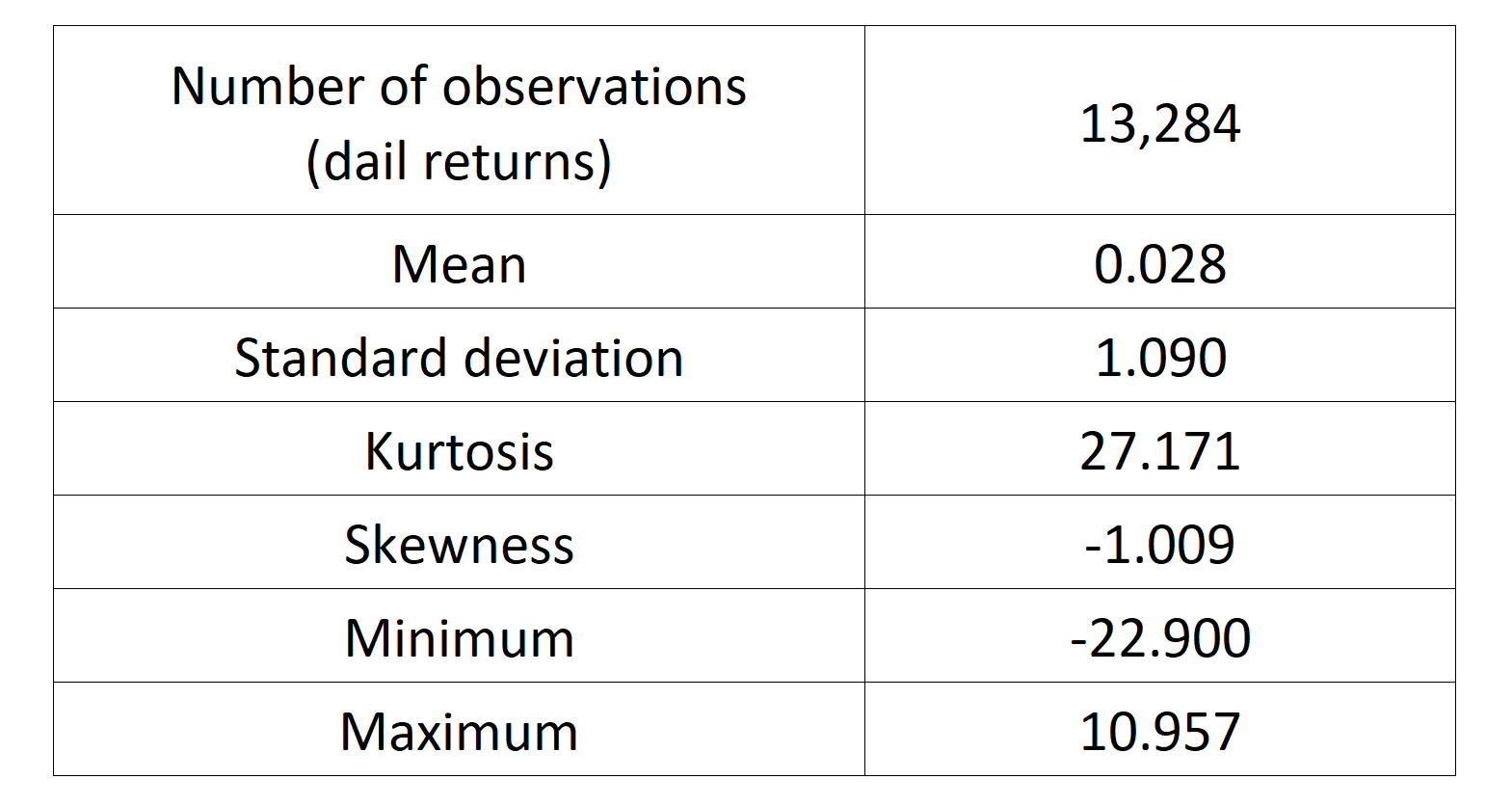
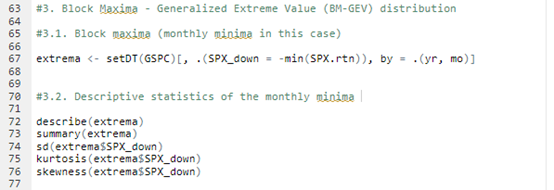
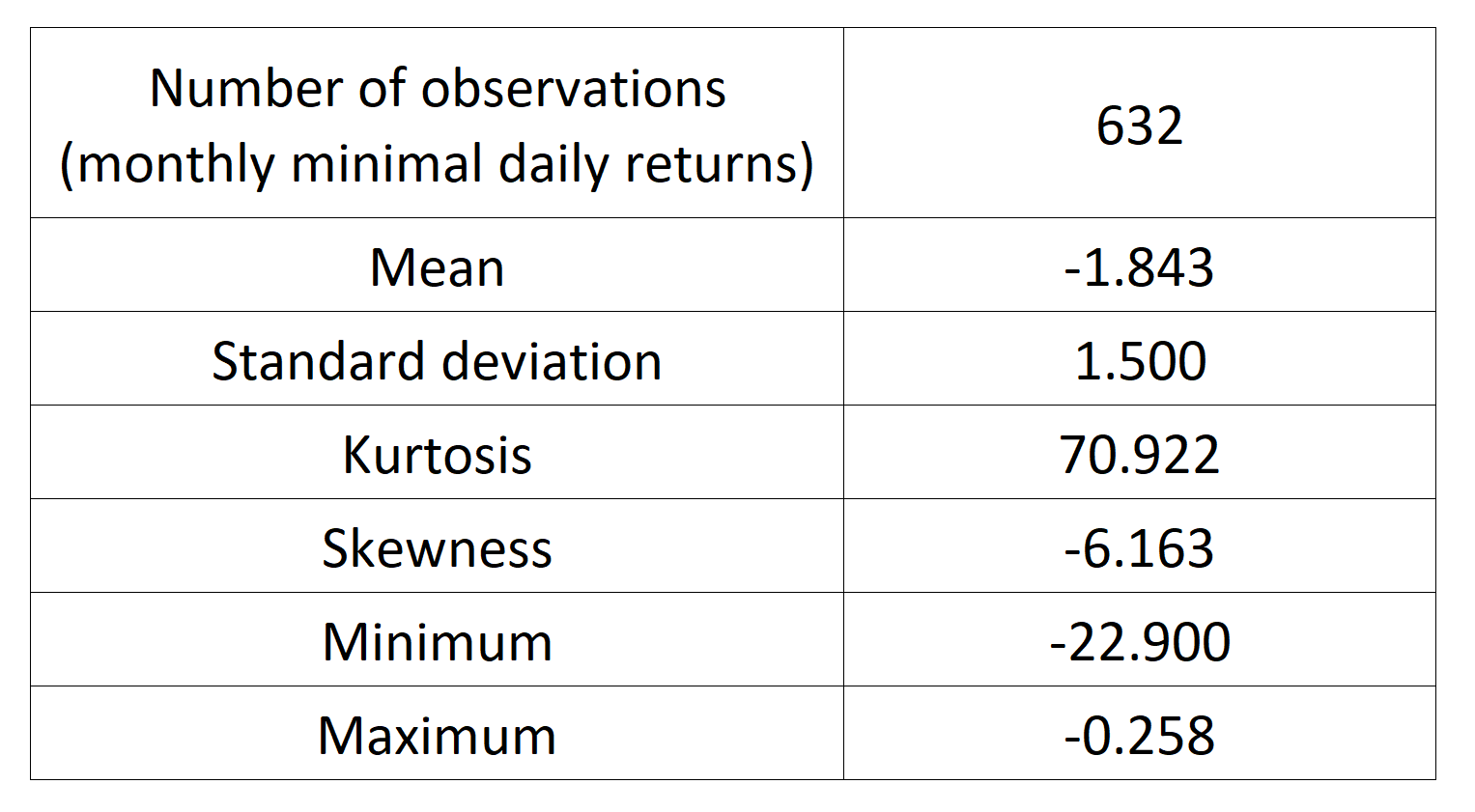

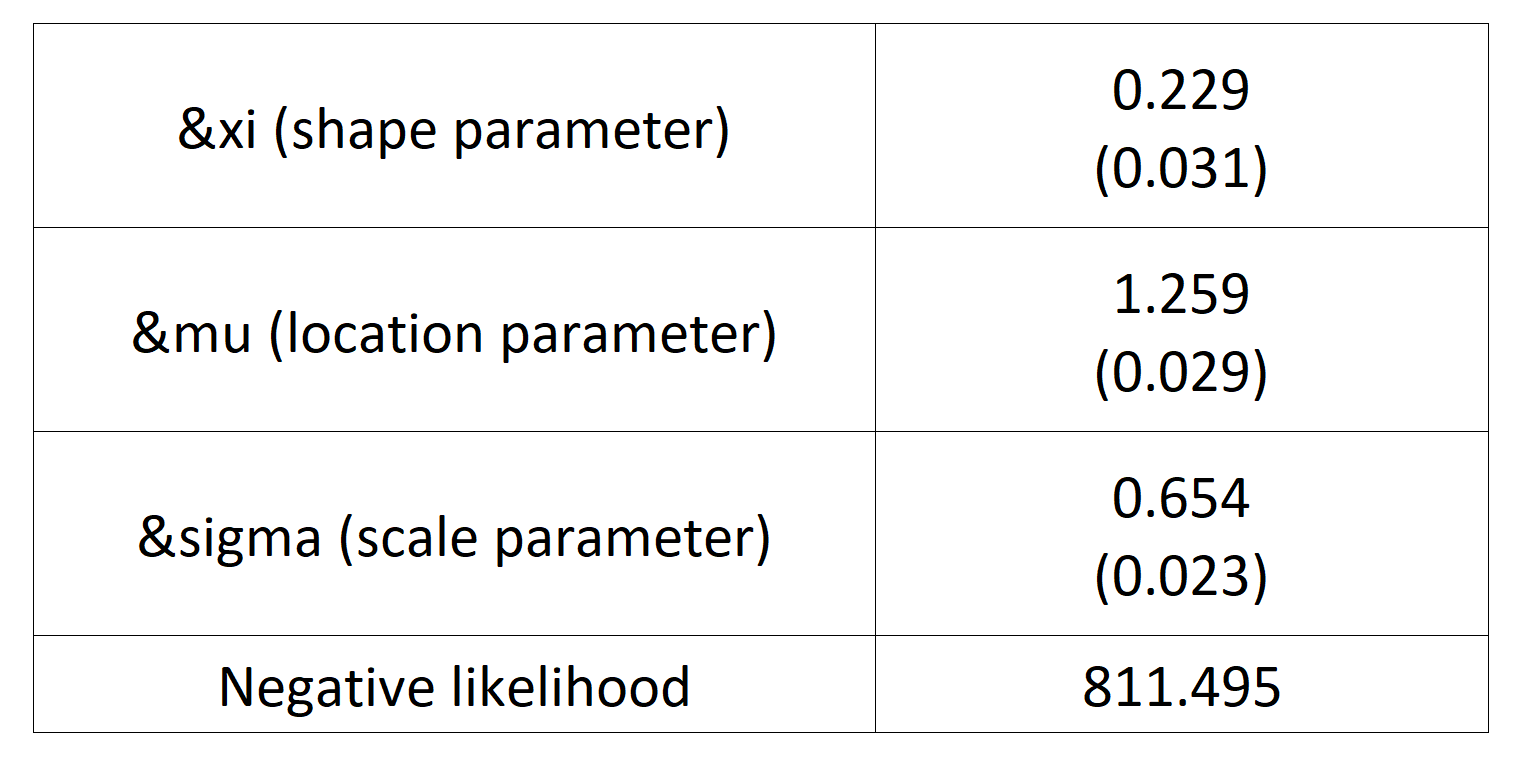
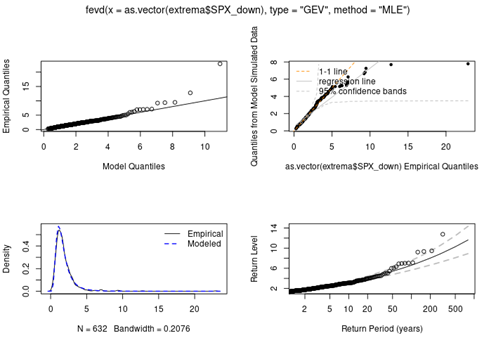
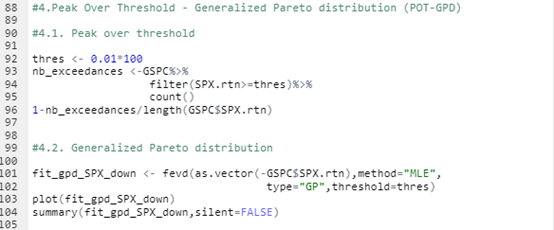



 Source : computation by the author.
Source : computation by the author.