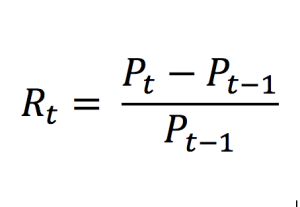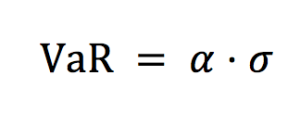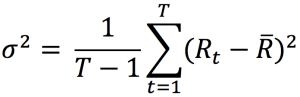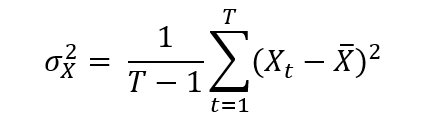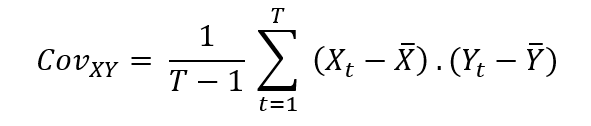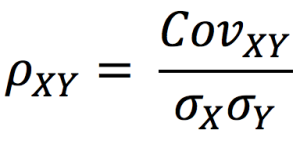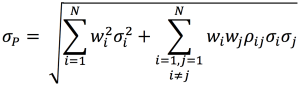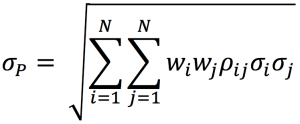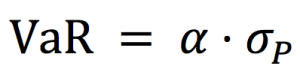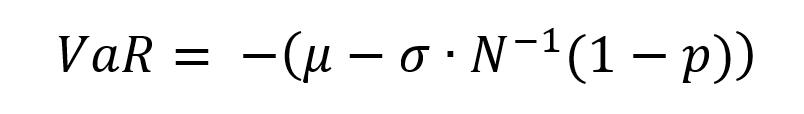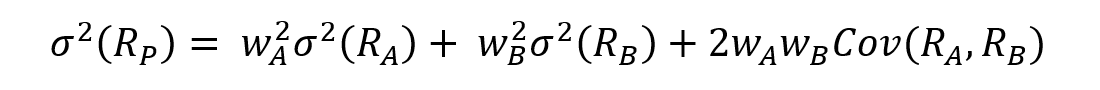VaR

Catégories de mesures de risques

by

Catégories de mesures de risque

Shengyu ZHENG

Dans cet article, Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2023) présente les catégories de mesures de risques couramment utilisées en finance.

Selon le type d’actif et l’objectif de gestion de risques, on se sert de mesures de risques de différentes catégories. Techniquement, on distingue trois catégories de mesures de risques selon l’objet statistique utilisé : la distribution statistique, la sensibilité et les scénarios. Généralement, les méthodes des différentes catégories sont employées et combinées, en constituant un système de gestion de risques qui facilite de différents niveaux des besoins managériaux.

Approche basée sur la distribution statistique

Les mesures modernes de risques s’intéressent à la distribution statistiques de la variation de valeur d’une positon de marché (ou de la rentabilité de cette position) à un horizon donné.

Les mesures se divise principalement en deux types, globales et locales. Les mesures globales (variance, beta) rendent compte de la distribution entière. Les mesures locales (Value-at-Risk, Expected Shortfall, Stress Value) se focalisent sur les queues de distribution, notamment la queue où se situent les pertes.

Cette approche n’est toutefois pas parfaite. Généralement un seul indicateur statistique n’est pas suffisant pour décrire tous les risques présents dans la position ou le portefeuille. Le calcul des propriétés statistiques et l’estimation des paramètres sont basés sur les données du passé, alors que le marché financier ne cesse d’évoluer. Même si la distribution reste inchangée entre temps, l’estimation précise de distribution n’est pas évidente et les hypothèses paramétriques ne sont pas toujours fiables.

Approche basée sur les sensibilités

Cette approche permet d’évaluer l’impact d’une variation d’un facteur de risques sur la valeur ou la rentabilité du portefeuille. Les mesures, telles que la duration et la convexité pour les obligations et les Grecques pour les produits dérivés, font partie de cette catégorie.

Elles comportent aussi des limites, notamment en termes d’agrégation de risques.

Approche basée sur les scénarios

Cette approche considère la perte maximale dans tous les scénarios générés sous les conditions de changements majeurs du marché. Les chocs peuvent s’agir, par exemple, d’une hausse de 10% d’un taux d’intérêt ou d’une devise, accompagnée d’une chute de 20% des indices d’actions importants.

Un test de résistance est un dispositif souvent mis en place par les banques centrales afin d’assurer la solvabilité des acteurs importants et la stabilité du marché financier. Un test de résistance, ou en anglicisme un « stress test », est un exercice consistance à simuler des conditions économiques et financières extrêmes mais effectivement plausibles, dans le but d’étudier les conséquences majeures apportées surtout aux établissements financiers (par exemple, les banques ou les assureurs), et de quantifier la capacité de résistance de ces établissements.

Autres article sur le blog SimTrade

▶ Shengyu ZHENG Mesures de risques

▶ Shengyu ZHENG Moments de la distribution

▶ Shengyu ZHENG Extreme Value Theory: the Block-Maxima approach and the Peak-Over-Threshold approach

▶ Youssef LOURAOUI Markowitz Modern Portfolio Theory

Resources

Academic research (articles)

Aboura S. (2009) The extreme downside risk of the S&P 500 stock index. Journal of Financial Transformation, 2009, 26 (26), pp.104-107.

Gnedenko, B. (1943). Sur la distribution limite du terme maximum d’une série aléatoire. Annals of mathematics, 423–453.

Hosking, J. R. M., Wallis, J. R., & Wood, E. F. (1985) “Estimation of the generalized extreme-value distribution by the method of probability-weighted moments” Technometrics, 27(3), 251–261.

Longin F. (1996) The asymptotic distribution of extreme stock market returns Journal of Business, 63, 383-408.

Longin F. (2000) From VaR to stress testing : the extreme value approach Journal of Banking and Finance, 24, 1097-1130.

Longin F. et B. Solnik (2001) Extreme correlation of international equity markets Journal of Finance, 56, 651-678.

Mises, R. v. (1936). La distribution de la plus grande de n valeurs. Rev. math. Union interbalcanique, 1, 141–160.

Pickands III, J. (1975). Statistical Inference Using Extreme Order Statistics. The Annals of Statistics, 3(1), 119– 131.

Academic research (books)

Embrechts P., C. Klüppelberg and T Mikosch (1997) Modelling Extremal Events for Insurance and Finance.

Embrechts P., R. Frey, McNeil A. J. (2022) Quantitative Risk Management, Princeton University Press.

Gumbel, E. J. (1958) Statistics of extremes. New York: Columbia University Press.

Longin F. (2016) Extreme events in finance: a handbook of extreme value theory and its applications Wiley Editions.

Other materials

Extreme Events in Finance

Rieder H. E. (2014) Extreme Value Theory: A primer (slides).

A propos de l’auteur

Cet article a été écrit en janvier 2023 par Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2023).

The Monte Carlo simulation method for VaR calculation

by

Jayati WALIA

In this article, Jayati WALIA (ESSEC Business School, Grande Ecole – Master in Management, 2019-2022) explains the Monte Carlo simulation method for VaR calculation.

Introduction

Monte Carlo simulations are a broad class of computational algorithms that rely majorly on repeated random sampling to obtain numerical results. The underlying concept is to model the multiple possible outcomes of an uncertain event. It is a technique used to understand the impact of risk and uncertainty in prediction and forecasting models.

The Monte Carlo simulation method was invented by John von Neumann (Hungarian-American mathematician and computer scientist) and Stanislaw Ulam (Polish mathematician) during World War II to improve decision making under uncertain conditions. It is named after the popular gambling destination Monte Carlo, located in Monaco and home to many famous casinos. This is because the random outcomes in the Monte Carlo modeling technique can be compared to games like roulette, dice and slot machines. In his autobiography, ‘Adventures of a Mathematician’, Ulam mentions that the method was named in honor of his uncle, who was a gambler.

Calculating VaR using Monte Carlo simulations

The basic concept behind the Monte Carlo approach is to repeatedly run a large number of simulations of a random process for a variable of interest (such as asset returns in finance) covering a wide range of possible scenarios. These variables are drawn from pre-specified probability distributions that are assumed to be known, including the analytical function and its parameters. Thus, Monte Carlo simulations inherently try to recreate the distribution of the return of a position, from which VaR can be computed.

Consider the CAC40 index as our asset of interest for which we will compute the VaR using Monte Carlo simulations.

The first step in the simulation is choosing a stochastic model for the behavior of our random variable (the return on the CAC 40 index in our case).
A common model is the normal distribution; however, in this case, we can easily compute the VaR from the normal distribution itself. The Monte Carlo simulation approach is more relevant when the stochastic model is more complex or when the asset is more complex, leading to difficulties to compute the VaR. For example, if we assume that returns follow a GARCH process, the (unconditional) VaR has to be computed with the Monte Carlo simulation methods. Similarly, if we consider complex financial products like options, the VaR has to be computed with the Monte Carlo simulation methods.

In this post, we compare the Monte Carlo simulation method with the historical method and the variance-covariance method. Thus, we simulate returns for the CAC40 index using the GARCH (1,1) model.
Figure 1 and 2 illustrate the GARCH simulated daily returns and volatility for the CAC40 index.

Figure 1. Simulated GARCH daily returns for the CAC40 index.
img_SimTrade_CAC40_GARCH_ret
Source: computation by the author.

Figure 2. Simulated GARCH daily volatility for the CAC40 index.
img_SimTrade_CAC40_GARCH_vol
Source: computation by the author.

Next, we sort the distribution of simulated returns in ascending order (basically in order of worst to best returns observed over the period). We can now interpret the VaR for the CAC40 index in one-day time horizon based on a selected confidence level (probability).

For instance, if we select a confidence level of 99%, then our VaR estimate corresponds to the 1st percentile of the probability distribution of daily returns (the bottom 1% of returns). In other words, there are 99% chances that we will not obtain a loss greater than our VaR estimate (for the 99% confidence level). Similarly, VaR for a 95% confidence level corresponds to bottom 5% of the returns.

Figure 3 below represents the unconditional probability distribution of returns for the CAC40 index assuming a GARCH process for the returns.

Figure 3. Probability distribution of returns for the CAC40 index.
img_SimTrade_CAC40_MonteCarloVaR
Source: computation by the author.

From the above graph, we can interpret VaR for 99% confidence level as -3% i.e., there is a 99% probability that daily returns we obtain in future are greater than -3%. Similarly, VaR for 95% confidence level as -1.72% i.e., there is a 95% probability that daily returns we obtain in future are greater than -1.72%.

You can download below the Excel file for computation of VaR for CAC40 stock using Monte Carlo method involving GARCH(1,1) model for simulation of returns.

Download the Excel file to compute the Monte Carlo VaR

Advantages and limitations of Monte Carlo method for VaR

The Monte Carlo method is a very powerful approach to VAR due its flexibility. It can potentially account for a wide range of scenarios. The simulations also account for nonlinear exposures and complex pricing patterns. In principle, the simulations can be extended to longer time horizons, which is essential for risk measurement and to model more complex models of expected returns.

This approach, however, involves investments in intellectual and systems development. It also requires more computing power than simpler methods since the more is the number of simulations generated, the wider is the range of potential scenarios or outcomes modelled and hence, greater would be the potential accuracy of VaR estimate. In practical applications, VaR measures using Monte Carlo simulation often takes hours to run. Time requirements, however, are being reduced significantly by advances in computer software and faster valuation methods.

Related posts on the SimTrade blog

   ▶ Jayati WALIA Quantitative Risk Management

   ▶ Jayati WALIA Value at Risk

   ▶ Jayati WALIA The historical method for VaR calculation

   ▶ Jayati WALIA The variance-covariance method for VaR calculation

   ▶ Jayati WALIA Brownian Motion in Finance

Useful resources

Jorion P. (2007) Value at Risk, Third Edition, Chapter 12 – Monte Carlo Methods, 321-326.

About the author

The article was written in March 2022 by Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).

Stress Testing used by Financial Institutions

by

Stress Testing used by Financial Institutions

Jayati WALIA

In this article, Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) introduces the concept of Stress testing used by financial institutions to estimate the impact of extraordinary market conditions characterized by a high level of volatility like stock market crashes.

Introduction

Asset price movements in financial markets are based on several local or global factors which can include economic developments, risk aversion, asset-specific financial information amongst others. These movements may lead to adverse situations which can cause unpredicted losses to financial institutions. Since the financial crisis of 2008, the need for resilience of financial institutions against market shocks has been exemplified, and regulators around the world have implemented strict measures to ensure financial stability and stress testing has become an imperative part of those measures.

Stress testing techniques were applied in the 1990s by most large international banks. In 1996, the need for stress testing by financial institutions was highlighted by the Basel Committee on Banking Supervision (BCBS) in its regulation recommendations (Basel Capital Accord). Following the 2008 financial crisis, focus on stress testing to ensure adequate capital requirements was further enhanced under the Dodd-Frank Wall Street reform Act (2010) in the United States.

Financial institutions use stress testing as a tool to assess the susceptibility of their portfolios to potential adverse market conditions and protect the capital thus ensuring stability. Institutions create extreme scenarios based on historical, hypothetical, or simulated macro-economic and financial information to measure the potential losses on their investments. These scenarios can incorporate single market variable (such as asset prices or interest rates) or a group of risk factors (such as asset correlations and volatilities).

Thus, stress tests are done using statistical models to simulate returns based on portfolio behavior under exceptional circumstances that help in gauging the asset quality and different risks including market risk, credit risk and liquidity risk. By using the results of the stress tests, the institutions evaluate the quality of their processes and implement further controls or measures required to strengthen them. They can also be prepared to use different hedging strategies to mitigate the potential losses in case of an adverse event.

Types of Stress testing

Stress testing can be based on different sets of information incorporated in the tests. These sets of information can be of two types: historical stress testing and hypothetical stress testing.

Historical stress testing

In this approach, market risk factors are analyzed using historical information to run the stress tests which can include incorporating information from previous crisis episodes in order to measure potential losses the portfolio may incur in case a similar situation reoccurs. For example, the downfall in S&P500 (approximately 30% during February 2020-March 2020) due to the Covid pandemic could be used to gauge future downsides if any such event occurs again. A drawback of this approach is that historical returns alone may not provide sufficient information about the likelihood of abnormal but plausible market events.

The extreme value theory can be used for calculation of VaR especially for stress testing. considers the distribution of extreme returns instead of all returns i.e., extreme price movements observed during usual periods (which correspond to the normal functioning of markets) and during highly volatile periods (which correspond to financial crises). Thus, these extreme values cover almost all market conditions ranging from the usual environments to periods of financial crises which are the focus of stress testing.

Hypothetical stress testing

In this method, hypothetical scenarios are constructed in order to measure the vulnerability of portfolios to different risk factors. Simulation techniques are implemented to anticipate scenarios that may incur extreme losses for the portfolios. For example, institutions may run a stress test to determine the impact of a decline of 3% in the GDP (Gross Domestic Product) of a country on their fixed income portfolio based in that country. However, a drawback of this approach is estimating the likelihood of the generated hypothetical scenario since there is no evidence to back the possibility of it ever happening.

EBA Regulations

In order to ensure the disciplined functioning and stability of the financial system in the EU, the European Banking Authority (EBA) facilitates the EU-wide stress tests in cooperation with European Central Bank (ECB), the European Systemic Risk Board (ESRB), the European Commission (EC) and the Competent Authorities (CAs) from all relevant national jurisdictions. These stress tests are conducted every 2 years and include the largest banks supervised directly by the ECB. The scenarios, key assumptions and guidelines implemented in the stress tests are jointly developed by EBA, ESRB, ECB and the European Commission and the individual and aggregated results are published by the EBA.

The purpose of this EU-wide stress testing is to assess how well banks are able to cope with potentially adverse economic and financial shocks. The stress test results help to identify banks’ vulnerabilities and address them through informed supervisory decisions.

Useful resources

Wikipedia: Stress testing

EBA Guidelines: EU-wide stress testing

Longin F. (2000) From VaR to stress testing : the extreme value approach” Journal of Banking and Finance N°24, pp 1097-1130.

Related Posts

   ▶ Walia J. Quantitative Risk Management

   ▶ Walia J. Value at Risk

   ▶ Walia J. The historical method for VaR calculation

   ▶ Walia J. The variance-covariance method for VaR calculation

About the author

Article written in January 2022 by Jayati Walia (ESSEC Business School, Master in Management, 2019-2022).

The historical method for VaR calculation

by

Jayati WALIA

In this article, Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) presents the historical method for VaR calculation.

Introduction

A key factor that forms the backbone for risk management is the measure of those potential losses that an institution is exposed to any investment. Various risk measures are used for this purpose and Value at Risk (VaR) is the most commonly used risk measure to quantify the level of risk and implement risk management.

VaR is typically defined as the maximum loss which should not be exceeded during a specific time period with a given probability level (or ‘confidence level’). VaR is used extensively to determine the level of risk exposure of an investment, portfolio or firm and calculate the extent of potential losses. Thus, VaR attempts to measure the risk of unexpected changes in prices (or return rates) within a given period. Mathematically, the VaR corresponds to the quantile of the distribution of returns.

The two key elements of VaR are a fixed period of time (say one or ten days) over which risk is assessed and a confidence level which is essentially the probability of the occurrence of loss-causing event (say 95% or 99%). There are various methods used to compute the VaR. In this post, we discuss in detail the historical method which is a popular way of estimating VaR.

Calculating VaR using the historical method

Historical VaR is a non-parametric method of VaR calculation. This methodology is based on the approach that the pattern of historical returns is indicative of the pattern of future returns.

The first step is to collect data on movements in market variables (such as equity prices, interest rates, commodity prices, etc.) over a long time period. Consider the daily price movements for CAC40 index within the past 2 years (512 trading days). We thus have 512 scenarios or cases that will act as our guide for future performance of the index i.e., the past 512 days will be representative of what will happen tomorrow.

For each day, we calculate the percentage change in price for the CAC40 index that defines our probability distribution for daily gains or losses. We can express the daily rate of returns for the index as:
img_historicalVaR_returns_formula

Where Rt represents the (arithmetic) return over the period [t-1, t] and Pt the price at time t (the closing price for daily data). Note that the logarithmic return is sometimes used (see my post on Returns).

Next, we sort the distribution of historical returns in ascending order (basically in order of worst to best returns observed over the period). We can now interpret the VaR for the CAC40 index in one-day time horizon based on a selected confidence level (probability).

Since the historical VaR is estimated directly from data without estimating or assuming any other parameters, hence it is a non-parametric method.

For instance, if we select a confidence level of 99%, then our VaR estimate corresponds to the 1st percentile of the probability distribution of daily returns (the top 1% of worst returns). In other words, there are 99% chances that we will not obtain a loss greater than our VaR estimate (for the 99% confidence level). Similarly, VaR for a 95% confidence level corresponds to top 5% of the worst returns.

Figure 1. Probability distribution of returns for the CAC40 index.
Historical method VaR
Source: computation by the author (data source: Bloomberg).

You can download below the Excel file for the VaR calculation with the historical method. The historical distribution is estimated with historical data from the CAC 40 index.

Download the Excel file to compute the historical VaR

From the above graph, we can interpret VaR for 90% confidence level as -3.99% i.e., there is a 90% probability that daily returns we obtain in future are greater than -3.99%. Similarly, VaR for 99% confidence level as -5.60% i.e., there is a 99% probability that daily returns we obtain in future are greater than -5.60%.

Advantages and limitations of the historical method

The historical method is a simple and fast method to calculate VaR. For a portfolio, it eliminates the need to estimate the variance-covariance matrix and simplifies the computations especially in cases of portfolios with a large number of assets. This method is also intuitive. VaR corresponds to a large loss sustained over an historical period that is known. Hence users can go back in time and explain the circumstances behind the VaR measure.

On the other hand, the historical method has a few of drawbacks. The assumption is that the past represents the immediate future is highly unlikely in the real world. Also, if the horizon window omits important events (like stock market booms and crashes), the distribution will not be well represented. Its calculation is only as strong as the number of correct data points measured that fully represent changing market dynamics even capturing crisis events that may have occurred such as the Covid-19 crisis in 2020 or the financial crisis in 2008. In fact, even if the data does capture all possible historical dynamics, it may not be sufficient because market will never entirely replicate past movements. Finally, the method assumes that the distribution is stationary. In practice, there may be significant and predictable time variation in risk.

Related posts on the SimTrade blog

   ▶ Jayati WALIA Quantitative Risk Management

   ▶ Jayati WALIA Value at Risk

   ▶ Jayati WALIA The variance-covariance method for VaR calculation

   ▶ Jayati WALIA The Monte Carlo simulation method for VaR calculation

Useful resources

Jorion, P. (2007) Value at Risk , Third Edition, Chapter 10 – VaR Methods, 276-279.

Longin F. (2000) From VaR to stress testing : the extreme value approach Journal of Banking and Finance, 24, 1097-1130.

About the author

The article was written in December 2021 by Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).

The variance-covariance method for VaR calculation

by

Jayati WALIA

In this article, Jayati WALIA (ESSEC Business School, Grande Ecole – Master in Management, 2019-2022) presents the variance-covariance method for VaR calculation.

Introduction

VaR is typically defined as the maximum loss which should not be exceeded during a specific time period with a given probability level (or ‘confidence level’). VaR is used extensively to determine the level of risk exposure of an investment, portfolio or firm and calculate the extent of potential losses. Thus, VaR attempts to measure the risk of unexpected changes in prices (or return rates) within a given period.

The two key elements of VaR are a fixed period of time (say one or ten days) over which risk is assessed and a confidence level which is essentially the probability of the occurrence of loss-causing event (say 95% or 99%). There are various methods used to compute the VaR. In this post, we discuss in detail the variance-covariance method for computing value at risk which is a parametric method of VaR calculation.

Assumptions

The variance-covariance method uses the variances and covariances of assets for VaR calculation and is hence a parametric method as it depends on the parameters of the probability distribution of price changes or returns.

The variance-covariance method assumes that asset returns are normally distributed around the mean of the bell-shaped probability distribution. Assets may have tendency to move up and down together or against each other. This method assumes that the standard deviation of asset returns and the correlations between asset returns are constant over time.

VaR for single asset

VaR calculation for a single asset is straightforward. From the distribution of returns calculated from daily price series, the standard deviation (σ) under a certain time horizon is estimated. The daily VaR is simply a function of the standard deviation and the desired confidence level and can be expressed as:

img_VaR_single_asset

Where the parameter ɑ links the quantile of the normal distribution and the standard deviation: ɑ = 2.33 for p = 99% and ɑ = 1.645 for p = 90%.

In practice, the variance (and then the standard deviation) is estimated from historical data.
img_VaR_asset_variance

Where Rt is the return on period [t-1, t] and R the average return.

Figure 1. Normal distribution for VaR for the CAC40 index
Normal distribution VaR for the CAC40 index
Source: computation by the author (data source: Bloomberg).

You can download below the Excel file for the VaR calculation with the variance-covariance method. The two parameters of the normal distribution (the mean and standard deviation) are estimated with historical data from the CAC 40 index.

Download the Excel file to compute the variance covariance method to VaR calculation

VaR for a portfolio of assets

Consider a portfolio P with N assets. The first step is to compute the variance-covariance matrix. The variance of returns for asset X can be expressed as:

Variance

To measure how assets vary with each other, we calculate the covariance. The covariance between returns of two assets X and Y can be expressed as:

Covariance

Where Xt and Yt are returns for asset X and Y on period [t-1, t].

Next, we compute the correlation coefficients as:

img_correlation_coefficient

We calculation the standard deviation of portfolio P with the following formula:

img_VaR_std_dev_portfolio

img_VaR_std_dev_portfolio_2

Where wi corresponds to portfolio weights of asset i.

Now we can estimate the VaR of our portfolio as:

img_portfolio_VaR

Where the parameter ɑ links the quantile of the normal distribution and the standard deviation: ɑ = 2.33 for p = 99% and ɑ = 1.65 for p = 95%.

Advantages and limitations of the variance-covariance method

Investors can estimate the probable loss value of their portfolios for different holding time periods and confidence levels. The variance–covariance approach helps us measure portfolio risk if returns are assumed to be distributed normally. However, the assumptions of return normality and constant covariances and correlations between assets in the portfolio may not hold true in real life.

Related posts on the SimTrade blog

▶ Jayati WALIA Quantitative Risk Management

▶ Jayati WALIA Value at Risk

▶ Jayati WALIA The historical method for VaR calculation

▶Jayati WALIA The Monte Carlo simulation method for VaR calculation

Useful resources

Jorion P. (2007) Value at Risk, Third Edition, Chapter 10 – VaR Methods, 274-276.

About the author

The article was written in December 2021 by Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).

Quantitative risk management

by

Quantitative risk management

Jayati WALIA

In this article, Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) presents Quantitative risk management.

Introduction

Risk refers to the degree of uncertainty in the future value of an investment or the potential losses that may occur. Risk management forms an integral part of any financial institution to safeguard the investments against different risks. The key question that forms the backbone for any risk management strategy is the degree of variability in the profit and loss statement for any investment.

The process of the risk management has three major phases. The first phase is risk identification which mainly focuses on identifying the risk factors to which the institution is exposed. This is followed by risk measurement that can be based on different types of metrics, from monitoring of open positions to using statistical models and Value-at-Risk. Finally, in the third phase risk management is performed by setting risk limits based on the determined risk appetite, back testing (testing the quality of the models on the historical data) and stress testing (assessing the impact of severe but still plausible adverse scenarios).

Different types of risks

There are several types of risks inherent in any investment. They can be categorized in the following ways:

Market risk

An institution can invest in a broad list of financial products including stocks, bonds, currencies, commodities, derivatives, and interest rate swaps. Market risk essentially refers to the risk arising from the fluctuation in the market prices of these assets that an institution trades or invests in. The changes in prices of these underlying assets due to market volatility can cause financial losses and hence, to analyze and hedge against this risk, institutions must constantly monitor the performance of the assets. After measuring the risk, they must also implement necessary measures to mitigate these risks to protect the institution’s capital. Several types of market risks include interest rate risk, equity risk, currency risk, credit spread risk etc.

Credit risk

The risk of not receiving promised repayments due to the counterparty failing to meet its obligations is essentially credit risk. The counterparty risk can arise from changes in the credit rating of the issuer or the client or a default on a due obligation. The default risk can arise from non-payments on any loans offered to the institution’s clients or partners. After the financial crisis of 2008-09, the importance of measuring and mitigating credit risks has increased many folds since the crisis was mainly caused by defaults on payments on sub-prime mortgages.

Operational risk

The risk of financial losses resulting from failed or faulty internal processes, people (human error or fraud) or system, or from external events like fraud, natural calamities, terrorism etc. refers to operational risk. Operational risks are generally difficult to measure and may cause potentially high impacts that cannot be anticipated.

Liquidity risk

The liquidity risk comprises to 2 types namely, market liquidity risk and funding liquidity risk. In market liquidity risk can arise from lack of marketability of an underlying asset i.e., the assets are comparatively illiquid or difficult to sell given a low market demand. Funding liquidity risk on the other hand refers to the ease with which institutions can raise funding and thus institutions must ensure that they can raise and retain debt capital to meet the margin or collateral calls on their leveraged positions.

Strategic risk

Strategic risks can arise from a poor strategic business decisions and include legal risk, reputational risk and systematic and model risks.

Basel Committee on Banking Supervision

The Basel Committee on Banking Supervision (BCBS) was formed in 1974 by central bankers from the G10 countries. The committee is headquartered in the office of the Bank for International Settlements (BIS) in Basel, Switzerland. BCBS is the primary global standard setter for the prudential regulation of banks and provides a forum for regular cooperation on banking supervisory matters. Its 45 members comprise central banks and bank supervisors from 28 jurisdictions. Member countries include Australia, Belgium, Canada, Brazil, China, France, Hong Kong, Italy, Germany, India, Korea, the United States, the United Kingdom, Luxembourg, Japan, Russia, Switzerland, Netherlands, Singapore, South Africa among many others.

Over the years, BCBS has developed influential policy recommendations concerning international banking and financial regulations in order to exercise judicious corporate governance and risk management (especially market, credit and operational risks), known as the Basel Accords. The key function of Basel accords is to manage banks’ capital requirements and ensure they hold enough cash reserves to meet their respective financial obligations and henceforth survive in any financial and/or economic distress.

Over the years, the following versions of the Basel accords have been released in order to enhance international banking regulatory frameworks and improve the sector’s ability to manage with financial distress, improve risk management and promote transparency:

Basel I

The first of the Basel accords, Basel I (also known as Basel Capital Accord) was developed in 1988 and implemented in the G10 countries by 1992. The regulations intended to improve the stability of the financial institutions by setting minimum capital reserve requirements for international banks and provided a framework for managing of credit risk through the risk-weighting of different assets which was also used for assessing banks’ credit worthiness.
However, there were many limitations to this accord, one of which being that Basel I only focused on credit risk ignoring other risk types like market risk, operational risk, strategic risk, macroeconomic conditions etc. that were not covered by the regulations. Also, the requirements posed by the accord were nearly the same for all banks, no matter what the bank’s risk level and activity type.

Basel II

Basel II regulations were developed in 2004 as an extension of Basel I, with a more comprehensive risk management framework and thereby including standardized measures for managing credit, operational and market risks. Basel II strengthened corporate supervisory mechanisms and market transparency by developing disclosure requirements for international regulations inducing market discipline.

Basel III

After the 2008 Financial Crisis, it was perceived by the BCBS that the Basel regulations still needed to be strengthened in areas like more efficient coverage of banks’ risk exposures and quality and measure of the regulatory capital corresponding to banks’ risks.
Basel III intends to correct the miscalculations of risk that were believed to have contributed to the crisis by requiring banks to hold higher percentages of their assets in more liquid instruments and get funding through more equity than debt. Basel III thus tries to strengthen resilience and reduce the risk of system-wide financial shocks and prevent future economic credit events. The Basel III regulations were introduced in 2009 and the implementation deadline was initially set for 2015 however, due to conflicting negotiations it has been repeatedly postponed and currently set to January 1, 2022.

Risk Measures

Efficient risk measurement based on relevant risk measures is a fundamental pillar of the risk management. The following are common measures used by institutions to facilitate quantitative risk management:

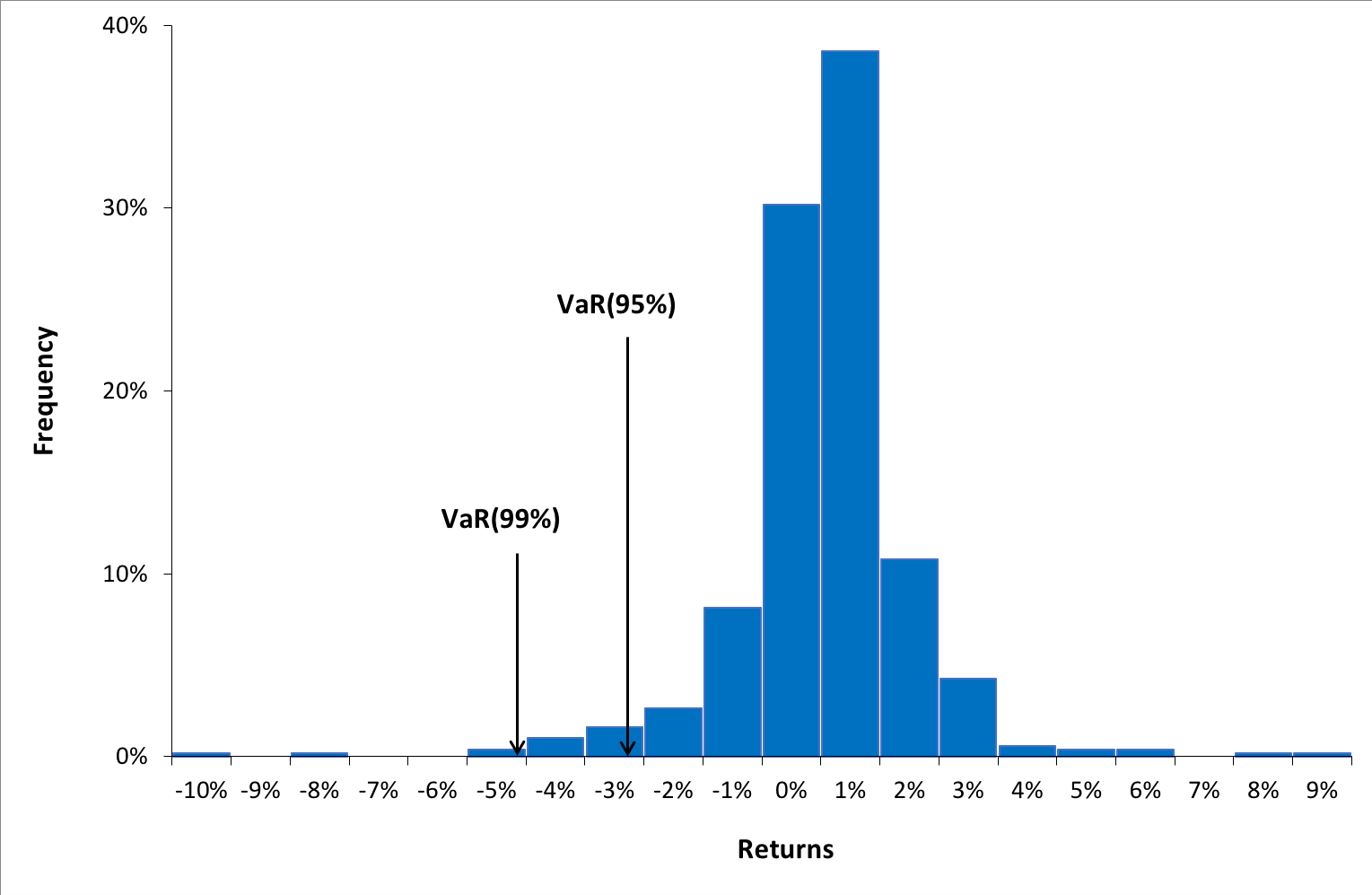
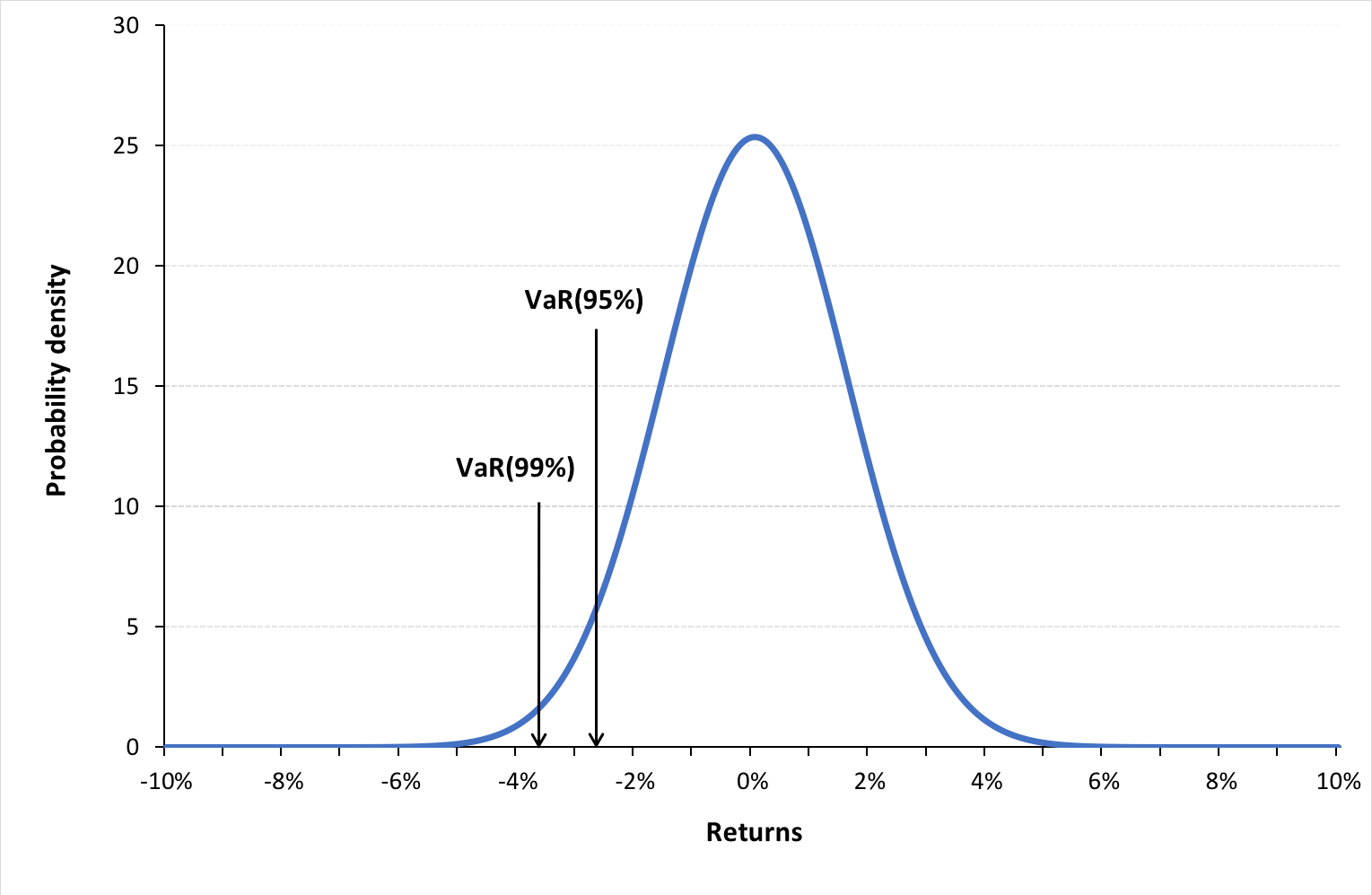
Value at risk (VaR)

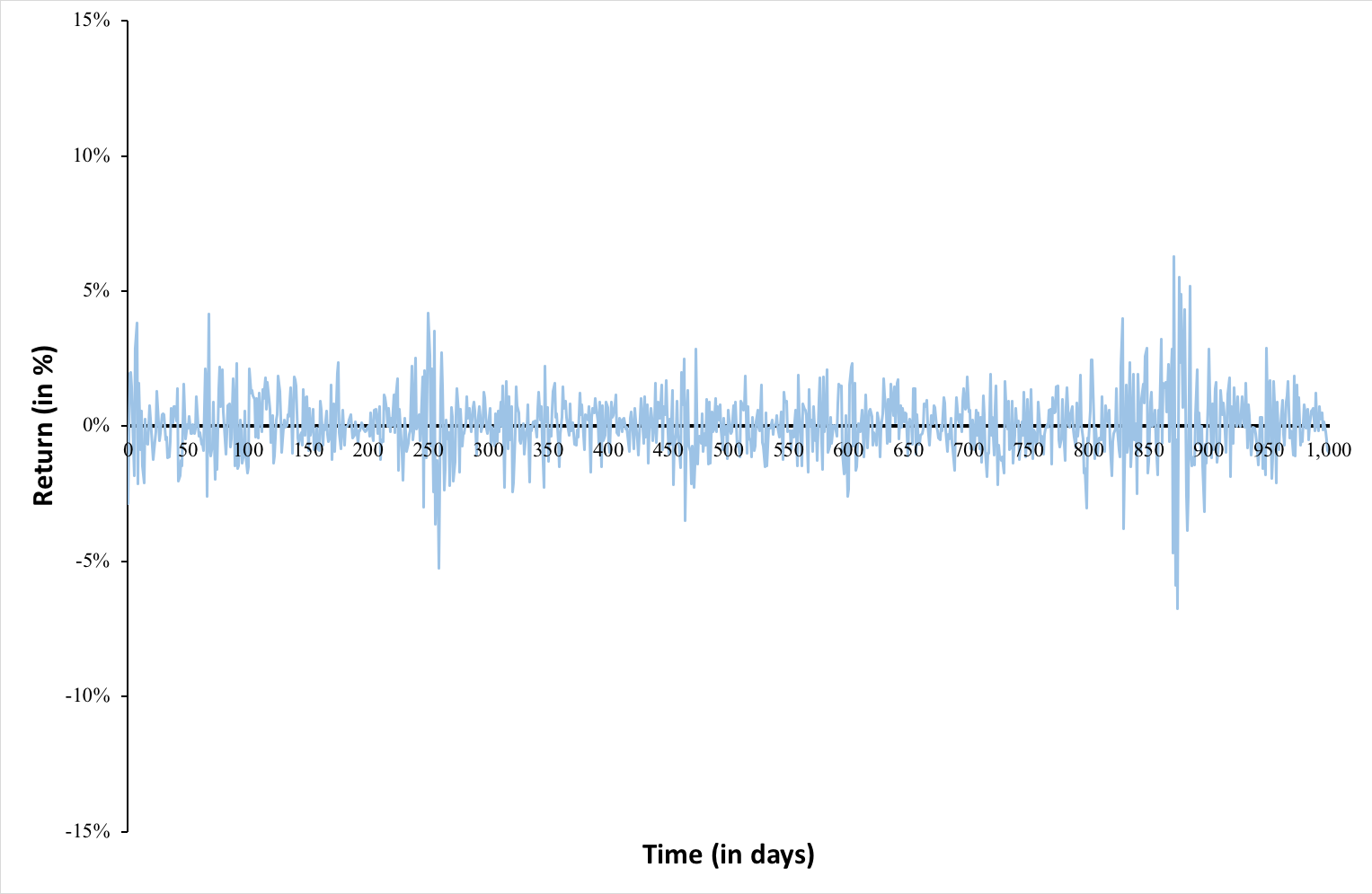
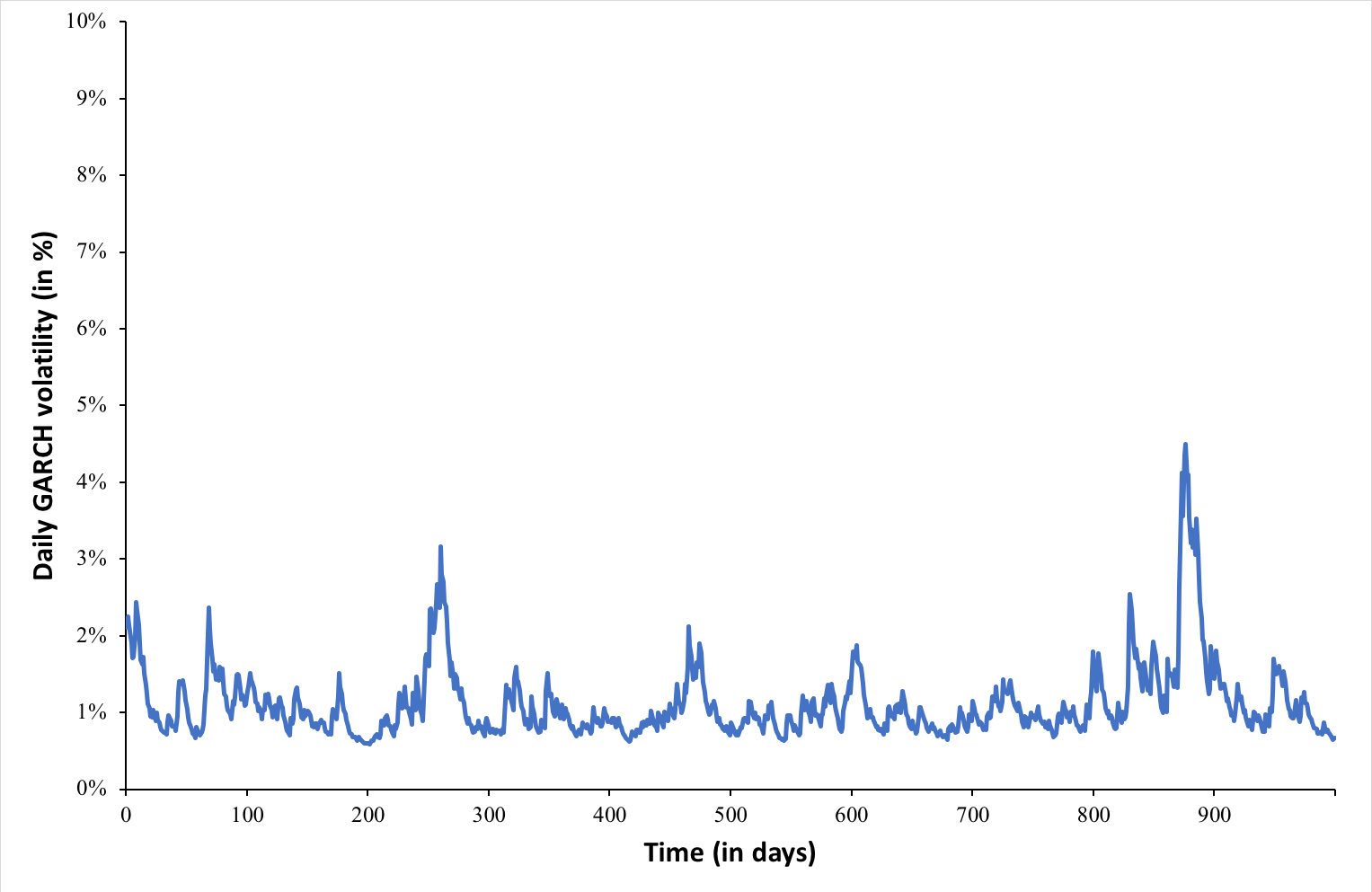
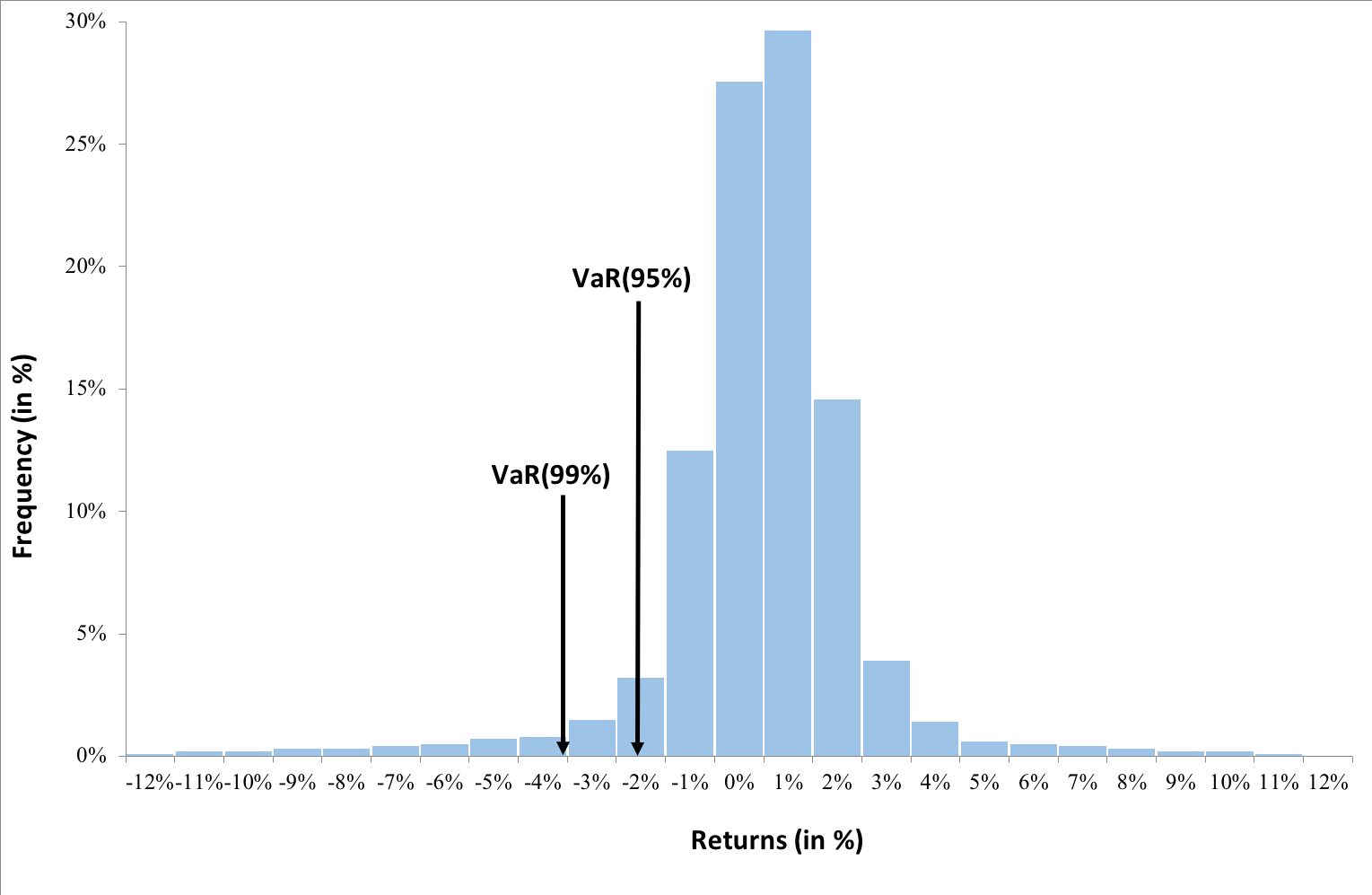
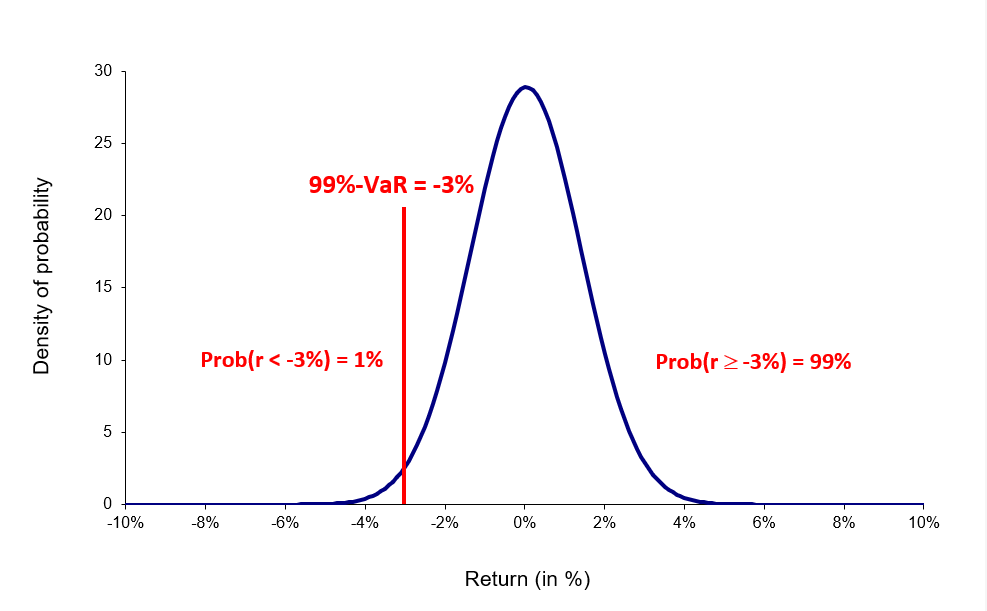
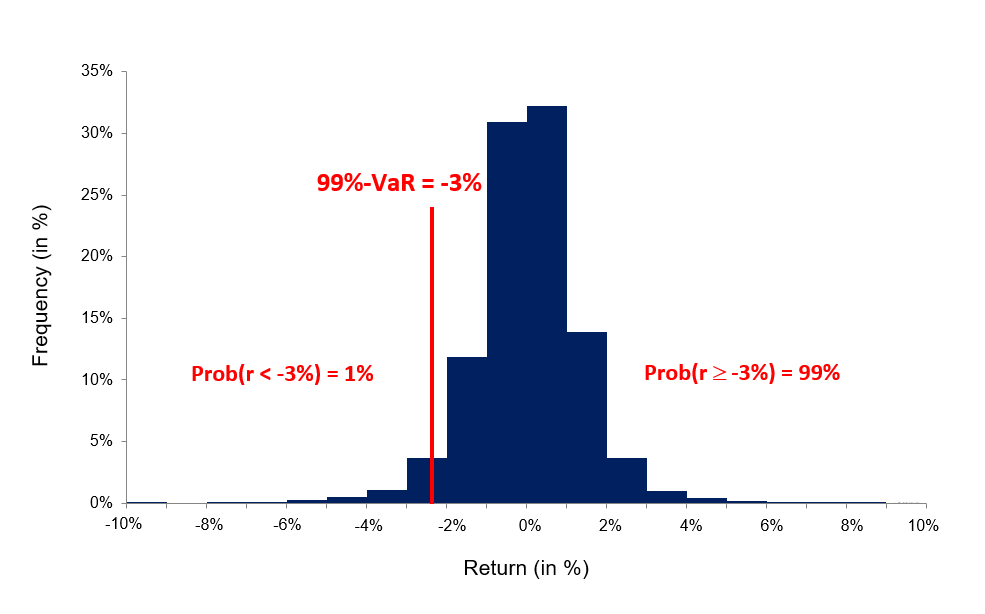
VaR is the most extensively used risk measure and essentially refers to the maximum loss that should not be exceeded during a specific period of time with a given probability. VaR is mainly used to calculate minimum capital requirements for institutions that are needed to fulfill their financial obligations, decide limits for asset management and allocation, calculate insurance premiums based on risk and set margin for derivatives transactions.
To estimate market risk, we model the statistical distribution of the changes in the market position. Usual models used for the task include normal distribution, the historical distribution and the distributions based on Monte Carlo simulations.

Expected Shortfall

The Expected Shortfall (ES) (also known as Conditional VaR (CVaR), Average Value at risk (AVaR), Expected Tail Loss (ETL) or Beyond the VaR (BVaR)) is a statistic measure used to quantify the market risk of a portfolio. This measure represents the expected loss when it is greater than the value of the VaR calculated with a specific probability level (also known as confidence level).

Credit Risk Measures

Probability of Default (PD) is the probability that a borrower may default on his debt over a period of 1 year. Exposure at Default (EAD) is the expected amount outstanding in case the borrower defaults and Loss given Default (LGD) refers to the amount expected to lose by the lender as a proportion of the EAD. Thus the expected loss in case of default is calculated as PD*EAD*LGD.

Related Posts on the SimTrade blog

   ▶ Jayati WALIA Value at Risk

   ▶ Akshit GUPTA Options

   ▶ Jayati WALIA Black-Scholes-Merton option pricing model

Useful resources

Articles

Longin F. (1996) The asymptotic distribution of extreme stock market returns Journal of Business, 63, 383-408.

Longin F. (2000) From VaR to stress testing : the extreme value approach Journal of Banking and Finance, 24, 1097-1130.

Longin F. and B. Solnik (2001) Extreme correlation of international equity markets Journal of Finance, 56, 651-678.

Books

Embrechts P., C. Klüppelberg and T Mikosch (1997) Modelling Extremal Events for Insurance and Finance.

Embrechts P., R. Frey, McNeil A. J. (2022) Quantitative Risk Management, Princeton University Press.

Gumbel, E. J. (1958) Statistics of extremes. New York: Columbia University Press.

Longin F. (2016) Extreme events in finance: a handbook of extreme value theory and its applications Wiley Editions.
Corporate Finance Institute Basel Accords

Other materials

Extreme Events in Finance

QRM Tutorial

About the author

The article was written in September 2021 by Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).

Value at Risk

by

Value at Risk

Jayati WALIA

In this article, Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) presents value at risk.

Introduction

Risk Management is a fundamental pillar of any financial institution to safeguard the investments and hedge against potential losses. The key factor that forms the backbone for any risk management strategy is the measure of those potential losses that an institution is exposed to for any investment. Various risk measures are used for this purpose and Value at Risk (VaR) is the most commonly used risk measure to quantify the level of risk and implement risk management.

VaR is typically defined as the maximum loss which should not be exceeded during a specific time period with a given probability level (or ‘confidence level’). Investments banks, commercial banks and other financial institutions extensively use VaR to determine the level of risk exposure of their investment and calculate the extent of potential losses. Thus, VaR attempts to measure the risk of unexpected changes in prices (or return rates) within a given period.

Mathematically, the VaR corresponds to the quantile of the distribution of returns on the investment.

VaR was not widely used prior to the mid 1990s, although its origin lies further back in time. In the aftermath of events involving the use of derivatives and leverage resulting in disastrous losses in the 1990s (like the failure of Barings bank), financial institutions looked for better comprehensive risk measures that could be implemented. In the last decade, VaR has become the standard measure of risk exposure in financial service firms and has even begun to find acceptance in non-financial service firms.

Computational methods

The three key elements of VaR are the specified level of loss, a fixed period of time over which risk is assessed, and a confidence interval which is essentially the probability of the occurrence of loss-causing event. The VaR can be computed for an individual asset, a portfolio of assets or for the entire financial institution. We detail below the methods used to compute the VaR.

Parametric methods

The most usual parametric method is the variance-covariance method based on the normal distribution.

In this method it is assumed that the price returns for any given asset in the position (and then the position itself) follow a normal distribution. Using the variance-covariance matrix of asset returns and the weights of the assets in the position, we can compute the standard deviation of the position returns denoted as σ. The VaR of the position can then simply computed as a function of the standard deviation and the desired probability level.

VaR Formula

Wherein, p represents the probability used to compute the VaR. For instance, if p is equal to 95%, then the VaR corresponds to the 5% quantile of the distribution of returns. We interpret the VaR as a measure of the loss we observe in 5 out of every 100 trading periods. N-1(x) is the inverse of the cumulative normal distribution function of the confidence level x.

Figure 1. VaR computed with the normal distribution.

VaR computed with the normal distribution

For a portfolio with several assets, the standard deviation is computed using the variance-covariance matrix. The expected return on a portfolio of assets is the market-weighted average of the expected returns on the individual assets in the portfolio. For instance, if a portfolio P contains assets A and B with weights wA and wB respectively, the variance of portfolio P’s returns would be:

Variance of portfolio

In the variance-covariance method, the volatility can be computed as the unconditional standard deviation of returns or can be calculated using more sophisticated models to consider the time-varying properties of volatility (like a simple moving average (SMA) or an exponentially weighted moving average (EWMA)).

The historical distribution

In this method, the historical data of past returns (for say 1,000 daily returns or 4 years of data) are used to build an historical distribution. VaR corresponds to the (1-p) quantile of the historical distribution of returns.
This methodology is based on the approach that the pattern of historical returns is indicative of future returns. VaR is estimated directly from data without estimating any other parameters hence, it is a non-parametric method.

Figure 2. VaR computed with the historical distribution.

VaR computed with the historical distribution

Monte Carlo Simulations

This method involves developing a model for generating future price returns and running multiple hypothetical trials through the model. The Monte Carlo simulation is the algorithm through which trials are generated randomly. The computation of VaR is similar to that in historical simulations. The difference only lies in the generation of future return which in case of the historical method is based on empirical data while it is based on simulated data in case of the Monte Carlo method.

The Monte Carlo simulation method is used for complex positions like derivatives where different risk factors (price, volatility, interest rate, dividends, etc.) must be considered.

Limitations of VaR

VaR doesn’t measure worst-case loss

VaR gives a percentage of loss that can be faced in a given confidence level, but it does not tell us about the amount of loss that can be incurred beyond the confidence level.

VaR is not additive

The combined VaR of two different portfolios may be higher than the sum of their individual VaRs.

VaR is only as good as its assumptions and input parameters

In VaR calculations especially parametric methods, unrealistic or inaccurate inputs can give misleading results for VaR. For instance, using the variance-covariance VaR method by assuming normal distribution of returns for assets and portfolios with non-normal skewness.

Different methods give different results

There are many approaches that have been defined over the years to estimate VaR. However, it essential to be careful in choosing the methodology keeping in mind the situation and characteristics of the portfolio or asset into consideration as different methods may be more accurate for specific scenarios.

Related posts on the SimTrade blog

   ▶ Jayati WALIA The variance-covariance method for VaR calculation

   ▶ Jayati WALIA The historical method for VaR calculation

   ▶ Jayati WALIA The Monte Carlo simulation method for VaR calculation

Useful Resources

Academic research articles

Artzner, P., F. Delbaen, J.-M. Eber, and D. Heath, (1999) Coherent Measures of Risk, Mathematical Finance, 9, 203-228.

Jorion P. (1997) “Value at Risk: The New Benchmark for Controlling Market Risk,” Chicago: The McGraw-Hill Company.

Longin F. (2000) From VaR to stress testing: the extreme value approach Journal of Banking and Finance, N°24, pp 1097-1130.

Longin F. (2016) Extreme events in finance: a handbook of extreme value theory and its applications Wiley Editions.

Longin F. (2001) Beyond the VaR Journal of Derivatives, 8, 36-48.

About the author

The article was written in September 2021 by Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).