Markowitz Modern Portfolio Theory
In this article, Youssef LOURAOUI (ESSEC Business School, Global Bachelor of Business Administration, 2017-2021) presents Markowitz’s Modern Portfolio Theory, a pioneering framework for understanding the impact of the number of stocks in a portfolio and their covariance relationships on portfolio diversification.
We begin by presenting Markowitz’s Modern Portfolio Theory (MPT) as the origin of factor investing (market factor). The assumptions of the model are then discussed. We’ll go through some of the model’s fundamental concepts next. We wrap up with a discussion of the concept’s limitations and a general conclusion.
Modern Portfolio Theory
The work conducted by Markowitz is widely acknowledged as a pioneer in financial economics and corporate finance for his theoretical implications and its application in financial markets. In 1990, Markowitz shared the Nobel Prize for his contributions to these domains, which he articulated in his 1952 article “Portfolio Selection” published in The Journal of Finance. His seminal work laid the groundwork for what is now often referred to as ‘Modern Portfolio Theory’ (MPT).
Modern portfolio theory was first introduced by the work of Harry Markowitz in 1952. Overall, the risk component of MPT can be quantified using various mathematical formulations and mitigated through the concept of diversification, which entails carefully selecting a weighted collection of investment assets that collectively exhibit lower risk characteristics than any single asset or asset class. Diversification is, in fact, the central notion of MPT and is predicated on the adage “never put all your eggs in one basket”.
Assumptions of the Markowitz Portfolio Theory
MPT is founded on several market and investor assumptions. Several of these assumptions are stated explicitly, while others are implied. Markowitz’s contributions to MPT in portfolio selection are based on the following basic assumptions:
- Investors are rational (they seek to maximize returns while minimizing risk).
- Investors will accept increased risk only if compensated with higher expected returns.
- Investors receive all pertinent information regarding their investment decision in a timely manner.
- Investors can borrow or lend an unlimited amount of capital at a risk-free rate of interest.
Concepts used in the MPT
Risk
Risk is equivalent to volatility in Markowitz’ portfolio selection theory—the larger the portfolio volatility, the greater the risk. Volatility is a term that refers to the degree of risk or uncertainty associated with the magnitude of variations in a security’s value. Risk is the possibility that an investment’s actual return will be less than predicted, which is technically quantified by standard deviation. A larger standard deviation implies a bigger risk and, hence, a larger potential return. If investors are prepared to take on risk, they anticipate earning a risk premium. Risk premium is defined as “the expected return on an investment that exceeds the risk-free rate of return”. The bigger the risk, the more risk premium investors need.”. Riskier investments do not necessarily provide a higher rate of return than risk-free ones. This is precisely why they are hazardous. However, historical evidence suggests that the only way for investors to obtain a better rate of return is to take on greater risk.
Systematic risk
Systematic risk is a type of risk at the macroeconomic level—risk that impacts a large number of assets to varying degrees. Inflation, interest rates, unemployment rates, currency exchange rates, and Gross National Product levels are all instances of systematic risk variables. These economic conditions have a significant influence on practically all securities. As a result, systemic risk cannot be completely eradicated.
Unsystematic risk
Unsystematic risk (or specific risk), on the other hand, is a type of risk that occurs at the micro-level risk factors that influence only a single asset or a small group of assets. It entails a distinct risk that is unrelated to other hazards and affects only particular securities or assets. For instance, Netflix’s poorly accepted adjustment to its planned consumer pricing structure elicited an extraordinarily unfavorable consumer response and defections, resulting in decreased earnings and stock prices. However, it had little effect on the Dow Jones or S&P 500 indexes, or on firms in the entertainment and media industries in general—with the probable exception of Netflix’s largest rival Blockbuster Video, whose value grew dramatically as a result of Netflix’s declining market share. Additional instances of unsystematic risk include a firm’s credit rating, poor newspaper coverage of a corporation, or a strike impacting a specific company. Diversification of assets within a portfolio can greatly minimize unsystematic risk.
Because the returns on various assets are, in fact, connected to some extent, unsystematic risk can never be totally avoided regardless of the number of asset classes pooled in a portfolio. The Markowitz Efficient Frontier is depicted in Figure 1, with all efficient portfolios on the upper line. The efficient frontier is a set of optimal portfolios that offer the best-projected return for a specified level of risk, or the lowest risk for a specified level of return. Portfolios that fall below the efficient frontier are inefficient because they do not generate a sufficient rate of return in relation to the level of risk (Figure 1).
Figure 1. Markowitz Efficient Frontier.
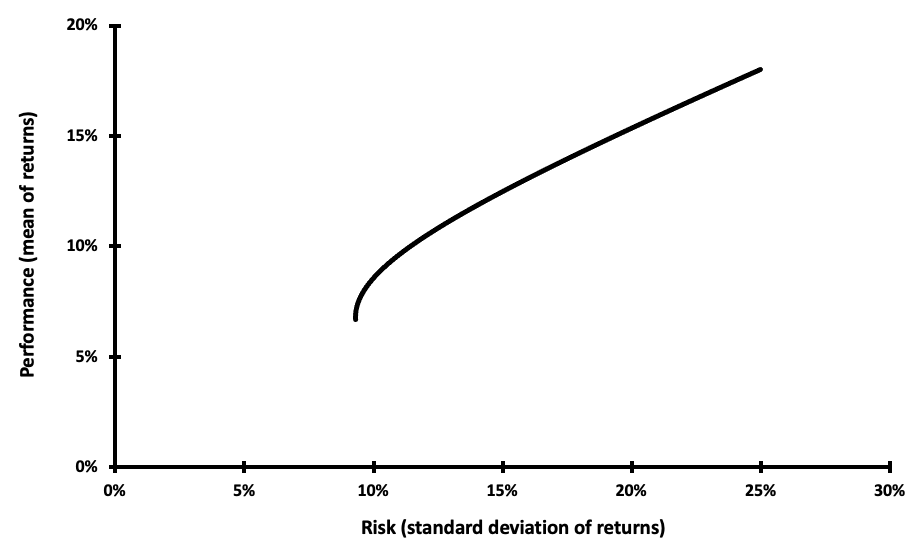
Source: computations by the author.
Risk-return trade-off
The term risk-return trade-off refers to Markowitz’s fundamental theory that the riskier an investment, the larger the necessary potential return (or expected return). Investors will generally retain a hazardous investment only if the predicted return is sufficiently high to compensate them for taking the risk. Markowitz derives a relation between expected return (μ) and variance (σ2p) captured in the following expression. Refer to the post Implementation of the Markowitz allocation model for a better understanding of the mathematical foundations of this approach:
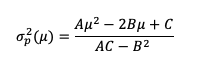
where
- A, B and C = Optimization parameters
- μ = expected return vector
Diversification
The words ‘diversification’ and ‘Diversification Effect’ relate to the correlations between portfolio risk and diversification. Diversification, a tenet of Markowitz’s portfolio selection theory and MPT, is a risk-reduction strategy that entails allocating assets among a variety of financial instruments, sectors, and other asset classes. In more straightforward terms, it refers to the aphorism “don’t put all your eggs in one basket.” If the basket is dropped, all eggs are shattered; if many baskets are used, the likelihood of all eggs being destroyed is significantly decreased. Diversification may be accomplished by investments in a variety of companies, asset types (e.g., bonds, real estate, etc.), and/or commodities such as gold or oil.
Diversification seeks to enhance returns while minimizing risk by investing in a variety of assets that will react differently to the same event (s). For example, whenever there is unfavorable news about the European debt crisis, the stock market typically declines dramatically. Simultaneously, the same news has generally benefited the price of specific commodities, such as gold. As a result, portfolio diversification methods should include not just diverse stocks inside and outside of the same industry, but also diverse asset classes, such as bonds and commodities. The Diversification Effect is a term that relates to the link between portfolio correlations and diversification. When there is an imperfect connection between assets (positive or negative), the diversification effect occurs. It is a critical and successful risk mitigation method since risk mitigation may be accomplished without jeopardizing profits. As a result, any prudent investor who is ‘risk cautious’ will diversify to a certain extent.
Limitation of the model
Despite its monumental theoretical significance, MPT has a slew of opponents who contend that its underlying assumptions and modeling of financial markets are frequently out of step with reality. One could argue that none of them are totally accurate and that each of them undermines MPT to varied degrees. Generally, some of the most common complaints include the following: irrationality of investors, relation between risk and return, treatment of information by investors, limitless borrowing capacity, perfectly efficient markets, and no taxes or transaction costs.
Irrationality of investors
It is assumed that investors are rational and aim to maximize returns while reducing risk. This is contrary to what market participants who become swept up in ‘herd behavior’ investment activity observe. For example, investors frequently gravitate into ‘hot’ industries, and markets frequently boom or burst because of speculative excesses.
Relation between risk and expected return
Increased risk = Increased expected returns. The idea that investors will only take more risk in exchange for higher predicted profits is regularly refuted by investor behavior. Frequently, investing techniques need investors to make a perceived hazardous investment (e.g., derivatives or futures) in order to lower total risk without increasing projected profits significantly. Additionally, investors may have certain utility functions that override worries about return distribution.
Treatment of information by investors
MPT anticipates that investors will get all information pertinent to their investment in a timely and thorough manner. In fact, global markets are characterized by information asymmetry (one party possesses superior knowledge), insider trading, and investors who are just more knowledgeable than others. This may explain why stocks, commercial assets, and enterprises are frequently acquired at a discount to their book or market value.
Limitless Borrowing Capacity
Another critical assumption mentioned previously is that investors have nearly unlimited borrowing capacity at a risk-free rate. Each investor has credit constraints in real-world markets. Additionally, only the federal government may borrow at the zero-interest treasury bill rate on a continuous basis.
Perfectly efficient markets
Markowitz’s theoretical contributions to MPT are predicated on the premise that markets are perfectly efficient (Markowitz, 1952). On the other hand, because MPT is based on asset values, it is susceptible to market whims such as environmental, personal, strategic, or social investment choice factors. Additionally, it ignores possible market failures like as externalities (costs or benefits that are not reflected in pricing), information asymmetry, and public goods (a non-rivalrous and non-excludable item). From another vantage point, centuries of ‘rushes’, ‘booms’, ‘busts’, ‘bubbles’, and ‘market crises’ illustrate that markets are far from efficient.
No Taxes or Transaction Costs
Neither taxes nor transaction costs are included in Markowitz’ theoretical contributions to MPT. To the contrary, genuine investment products are subject to both taxes and transaction costs (e.g., broker fees, administrative charges, and so on), and considering these costs into portfolio selection may certainly affect the optimal portfolio composition.
Conclusion
MPT has become the de facto dogma of contemporary financial theory and practice. The idea of MPT is that beating the market is tough, and those that do do it by diversifying their portfolios properly and taking above-average investing risks. The critical point to remember is that the model is only a tool—albeit the most powerful hammer in one’s financial toolbox. It has been over sixty years since Markowitz introduced MPT, and its popularity is unlikely to decrease anytime soon. His theoretical insights have served as the foundation for more theoretical investigation in the field of portfolio theory. Nonetheless, Markowitz’s portfolio theory is susceptible to and dependent on ongoing ‘probabilistic’ development and expansion.
Why should I be interested in this post?
Modern Portfolio Theory is at the heart of modern finance and its core foundations are structuring the modern investing panorama. MPT has established itself as the foundation for modern financial theory and practice. MPT’s premise is that beating the market is difficult, and those that do it by diversifying their portfolios appropriately and accepting higher-than-average investment risks.
MPT has been around for almost sixty years, and its popularity is unlikely to wane anytime soon. His theoretical contributions have laid the groundwork for more theoretical research in the field of portfolio theory. Markowitz’s portfolio theory, however, is vulnerable to and dependent on continuing ‘probabilistic’ development and expansion.
Related posts on the SimTrade blog
Portfolio Theory
▶ Youssef LOURAOUI Implementation of the Markowitz allocation model
▶ Youssef LOURAOUI Capital Asset Pricing Model (CAPM)
▶ Youssef LOURAOUI Implementation of the Black-Litterman model
▶ Youssef LOURAOUI Black-Litterman model
Factor investing
▶ Youssef LOURAOUI Factor Investing
▶ Youssef LOURAOUI Is smart beta really smart?
Factors
▶ Youssef LOURAOUI Size Factor
▶ Youssef LOURAOUI Value Factor
▶ Youssef LOURAOUI Yield Factor
▶ Youssef LOURAOUI Momentum Factor
▶ Youssef LOURAOUI Quality Factor
▶ Youssef LOURAOUI Growth Factor
▶ Youssef LOURAOUI Minimum Volatility Factor
Useful resources
Academic research
Ang, A., 2013. Factor Investing. Working paper.
Mangram, M.E., 2013. A simplified perspective of the Markowitz Portfolio Theory. Global Journal of Business Research, 7(1): 59-70.
Markowitz, H., 1952. Portfolio Selection. The Journal of Finance, 7(1): 77-91.
Mossin, J. 1966. Equilibrium in a Capital Asset Market. Econometrica, 34(4): 768-783.
Sharpe, W.F. 1963. A Simplified Model for Portfolio Analysis. Management Science, 9(2): 277-293.
Sharpe, W.F. 1964. Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk. The Journal of Finance, 19(3): 425-442.
About the author
The article was written in September 2021 by Youssef LOURAOUI (ESSEC Business School, Global Bachelor of Business Administration, 2017-2021).


2 thoughts on “Markowitz Modern Portfolio Theory”
Comments are closed.