Pricing barrier options with analytical formulas
As is mentioned in the previous post, the frequency of monitoring is one of the determinants of the price of a barrier option. The higher the frequency, the more likely a barrier event would take place.
In this article, Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2023) explains the pricing of continuously and discretely monitored barrier options with analytical formulas.
Pricing of standard continuously monitored barrier options
For pricing standard barrier options, we cannot simply apply the Black-Sholes-Merton Formula for the particularity of the barrier conditions. There are, however, several models available developed on top of this theoretical basis. Among them, models developed by Merton (1973), Reiner and Rubinstein (1991) and Rich (1994) enabled the pricing of continuously monitored barrier options to be conducted in a formulaic fashion. They are concisely put together by Haug (1997) as follows:

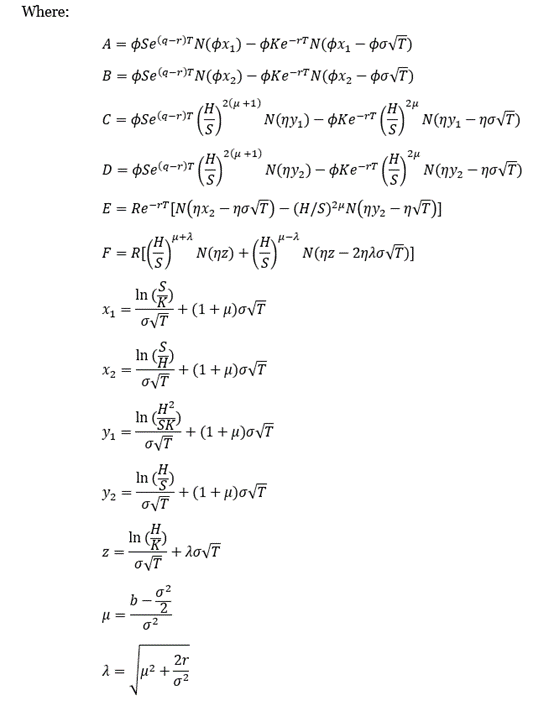

Pricing of standard discretely monitored barrier options
For discretely monitored barrier options, Broadie and Glasserman (1997) derived an adjustment that is applicable on top of the pricing formulas of the continuously monitored counterparts.
Let’s denote:

The price of a discretely monitored barrier option of a certain barrier price equals the price of a continuously monitored barrier option of the adjusted price plus an error:
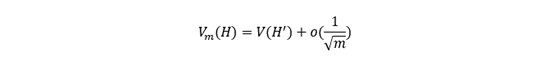
The adjusted barrier price, in this case, would be:
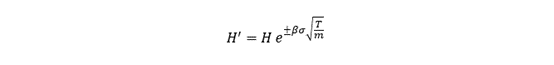

It is also worth noting that the error term o(·) grows prominently when the barrier approaches the strike price. A threshold of 5% from the strike price should be imposed if this approach is employed for pricing discretely monitored barrier options.
Example of pricing a down-and-out put with R with the formulaic approach
The general setup of economic details of the Down-and-Out Put and related market information is presented as follows:
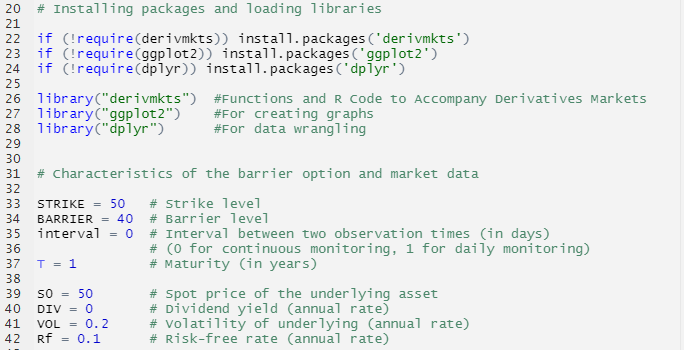
There are built-in functions in the “derivmkts” library that render directly the prices of barrier options of continuous monitoring, such as calldownin(), callupin(), calldownout(), callupout(), putdownin(), putupin(), putdownout(), and putupout (). By incorporating the adjustment proposed by Broadie and Glasserman (1997), all barrier options of both monitoring methods could be priced in a formulaic way with the following function:
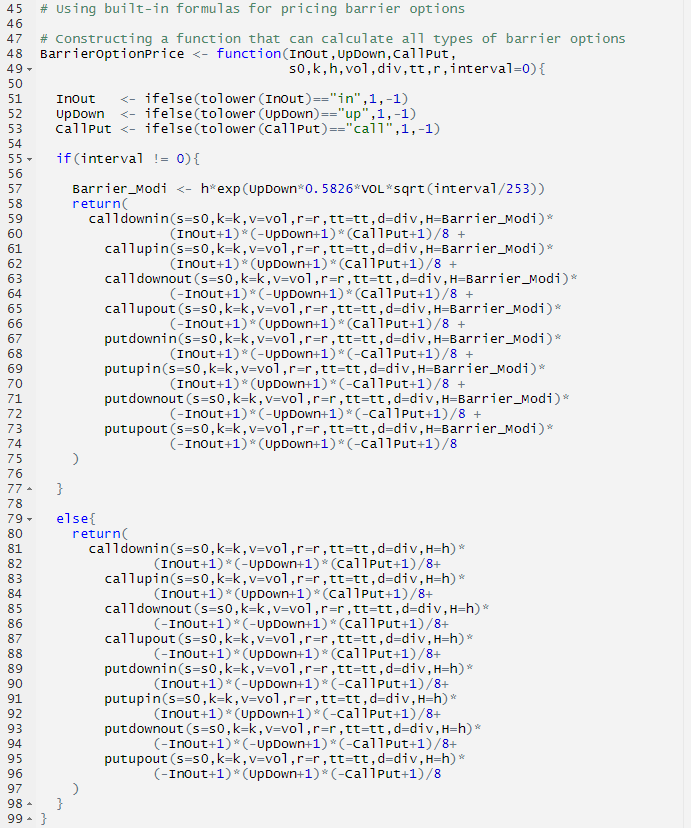
For example, for a down-and-out Put option with the aforementioned parameters, we can use this function to calculate the prices.

For continuous monitoring, we get a price of 0.6264298, and for daily discrete monitoring, we get a price of 0.676141. It makes sense that for a down-and-out put option, a lower frequency of barrier monitoring means less probability of a knock-out event, thus less protection for the seller from extreme downside price trajectories. Therefore, the seller would charge a higher premium for this put option.
Download R file to price barrier options
You can find below an R file (file with txt format) to price barrier options.
Why should I be interested in this post?
As one of the most traded but the simplest exotic derivative products, barrier options open an avenue for different applications. They are also very often incorporated in structured products, such as reverse convertibles. It is, therefore, important to understand the elements having an impact on their prices and the closed-form pricing formulas are a good presentation of these elements.
Related posts on the SimTrade blog
▶ Shengyu ZHENG Barrier options
▶ Shengyu ZHENG Pricing barrier options with simulations and sensitivity analysis with Greeks
Useful resources
Academic research articles
Broadie, M., Glasserman P., Kou S. (1997) A Continuity Correction for Discrete Barrier Option. Mathematical Finance, 7:325-349.
Merton, R. (1973) Theory of Rational Option Pricing. The Bell Journal of Economics and Management Science, 4:141-183.
Paixao, T. (2012) A Guide to Structured Products – Reverse Convertible on S&P500
Reiner, E.S., Rubinstein, M. (1991) Breaking down the barriers. Risk Magazine, 4(8), 28–35.
Rich, D. R. (1994) The Mathematical Foundations of Barrier Option-Pricing Theory. Advances in Futures and Options Research: A Research Annual, 7:267-311.
Wang, B., Wang, L. (2011) Pricing Barrier Options using Monte Carlo Methods, Working paper.
Books
Haug, E. (1997) The Complete Guide to Option Pricing. London/New York: McGraw-Hill.
Hull, J. (2006) Options, Futures, and Other Derivatives. Upper Saddle River, N.J: Pearson/Prentice Hall.
About the author
The article was written in July 2022 by Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2023).


