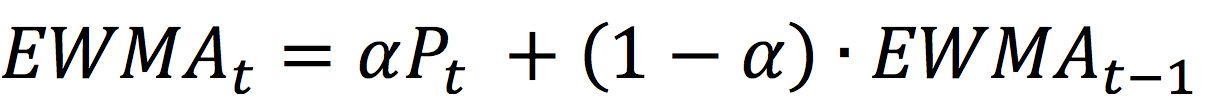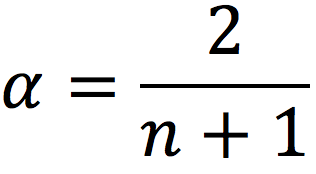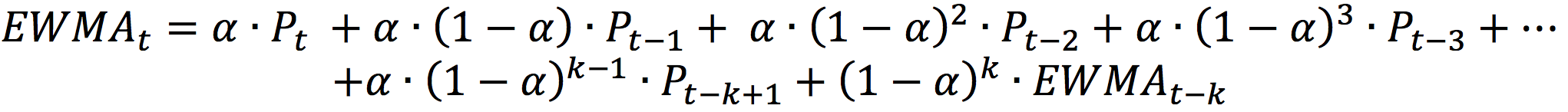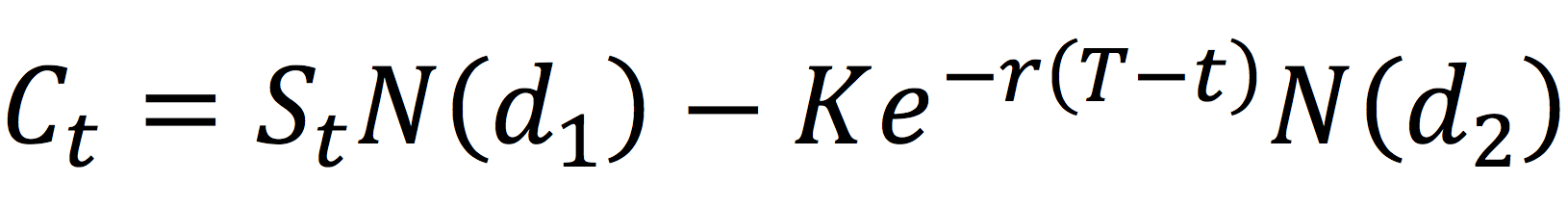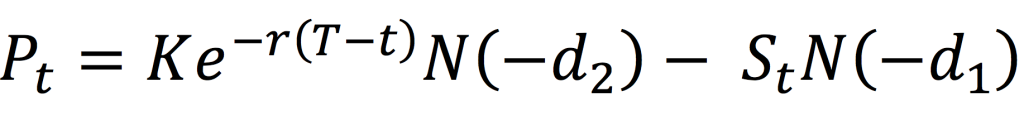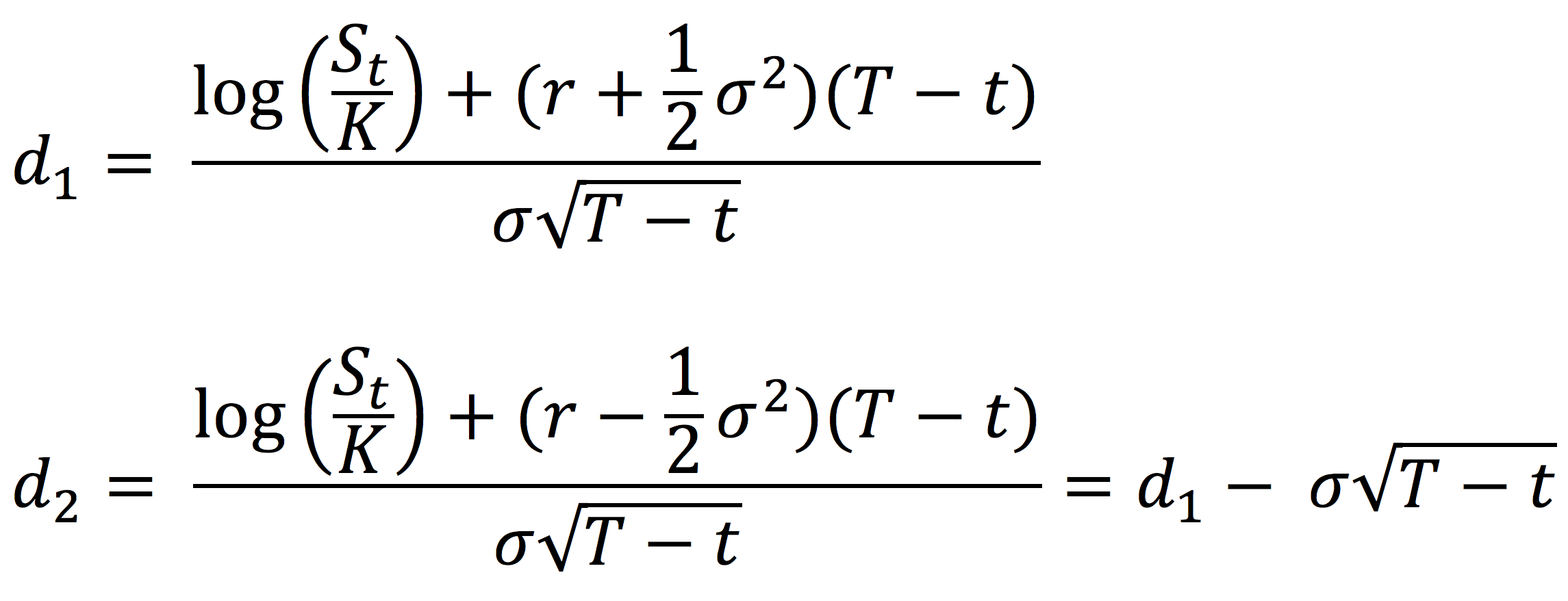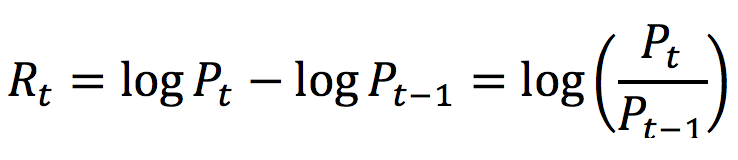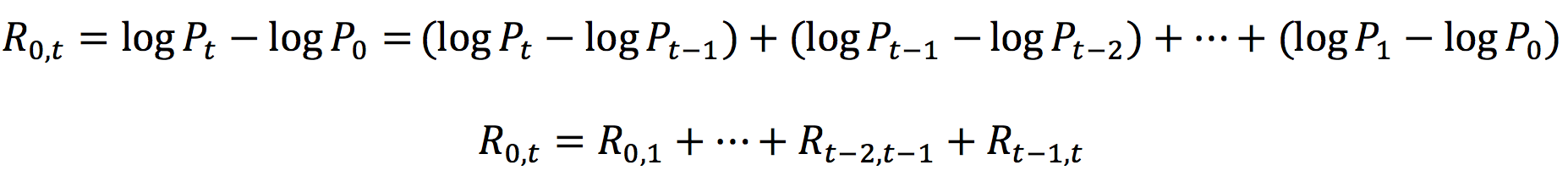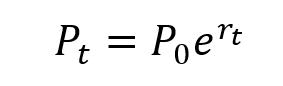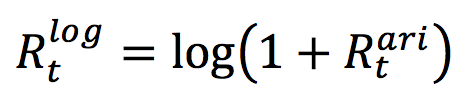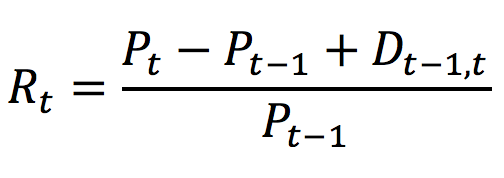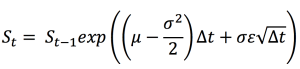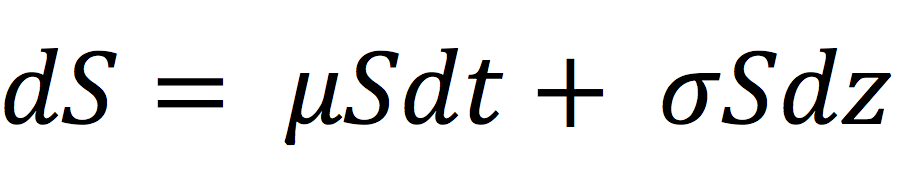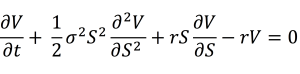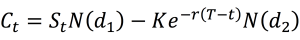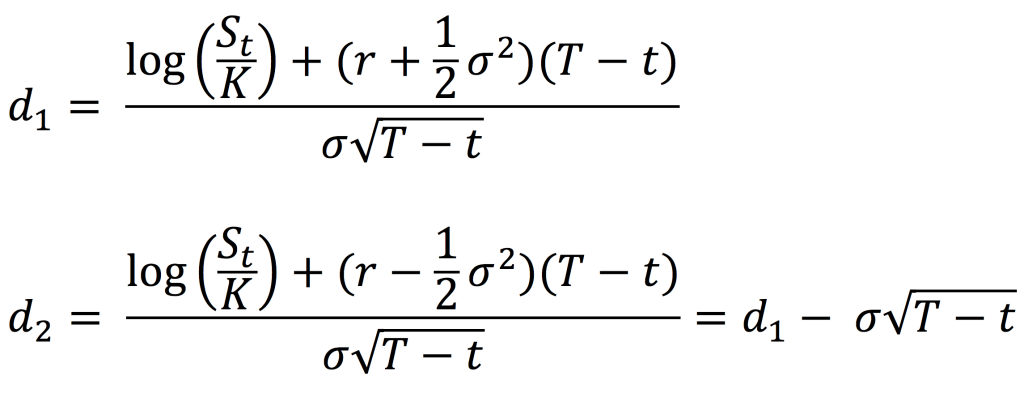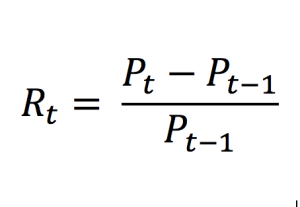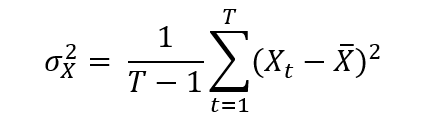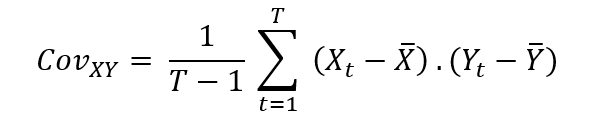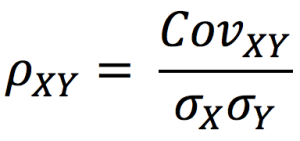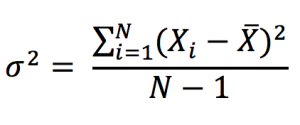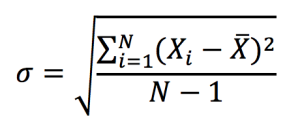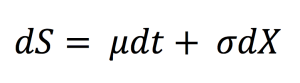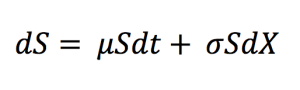In this article, Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) explains currency overlay which is a mechanism to effectively manage currency risk in asset portfolios.
Overview
Currency risk, also known as exchange-rate risk, forex exchange or FX risk, is a kind of market risk that is caused by the fluctuations in currency exchange rates.
Both individual and institutional investors are diversifying their portfolios through assets in international financial markets, but by doing so they also introduce currency risk in their portfolios.
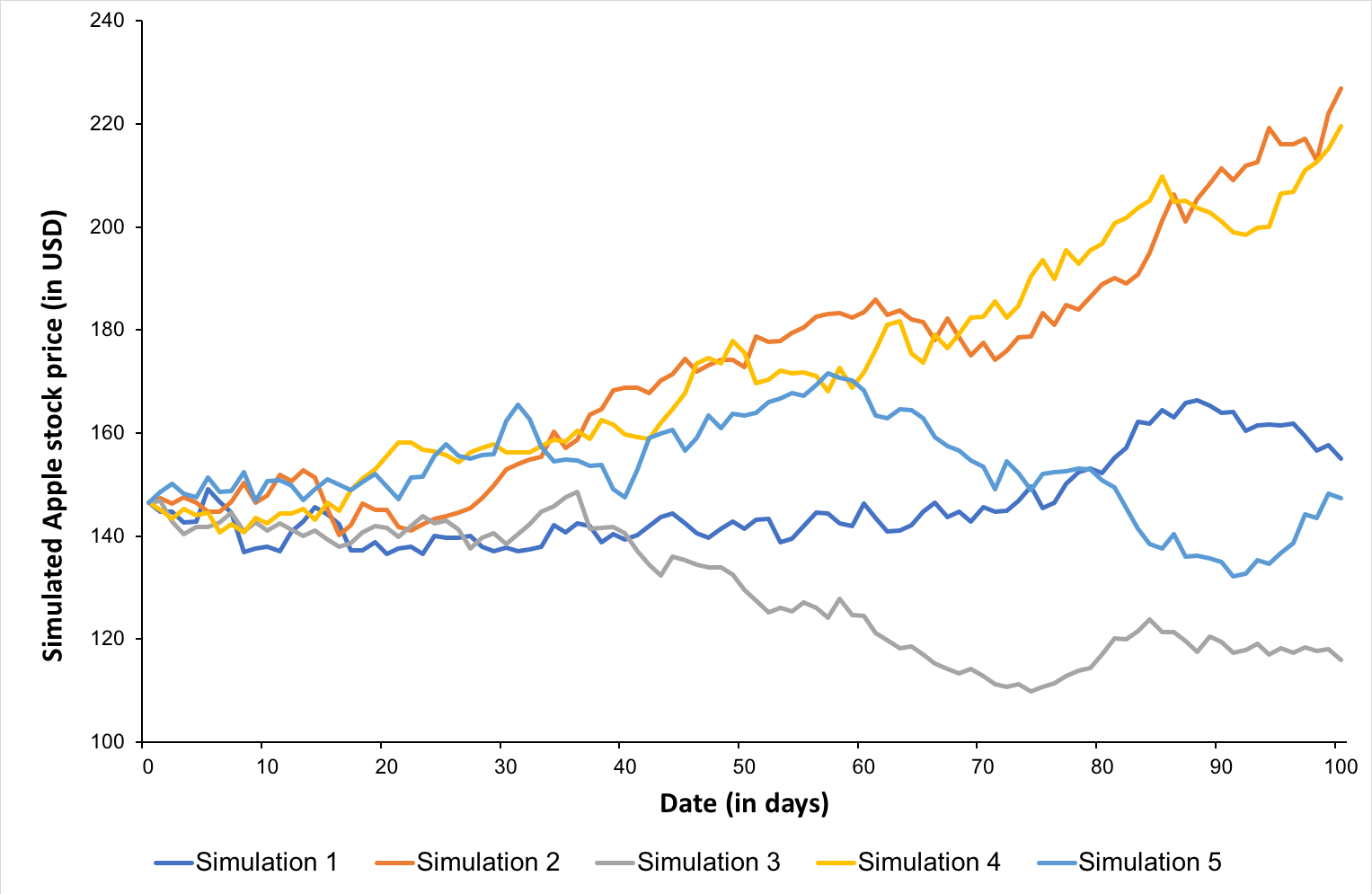
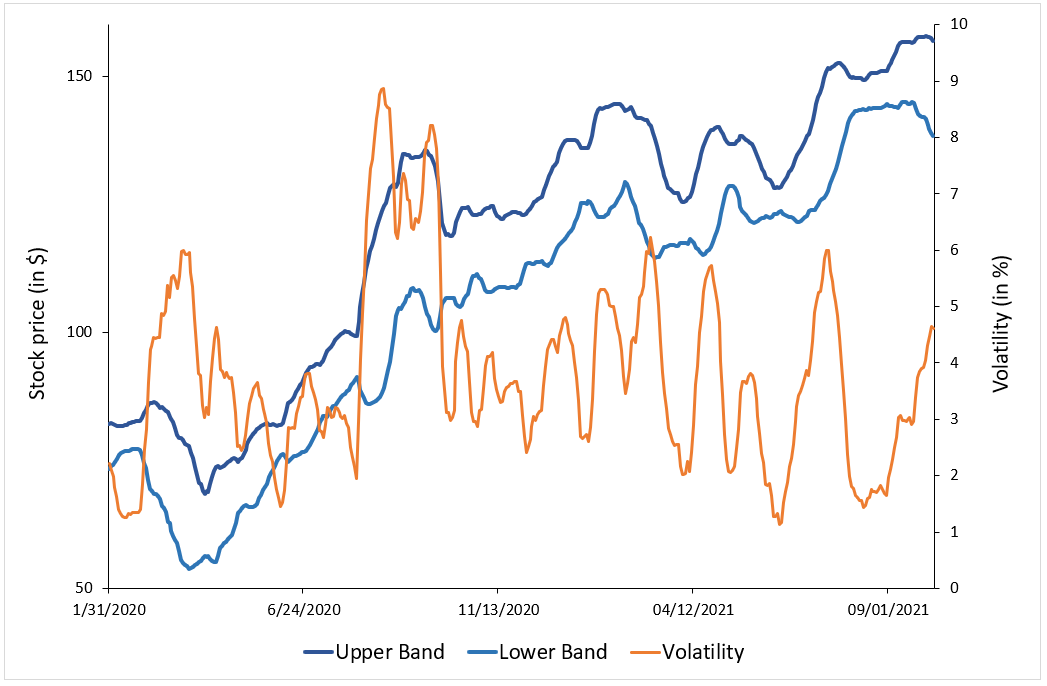
Consider an investor in the US who decides to invest in the French equity market (say in the CAC 40 index). The investor is now exposed to currency risk due to the movements in EURUSD exchange rate. You can download the Excel file below which illustrates the impact of the EURUSD exchange rate on the overall performance of the investor’s portfolio.
This exercise demonstrates the importance of currency risk in managing an equity portfolio with assets dominated in foreign currencies. We can observe that over a one-month time-period (July 19 – August 19, 2022), the annual volatility of the American investor’s portfolio with FX risk included is 12.96%. On the other hand, if he hedges the FX risk (using a currency overlay strategy), the annual volatility of his portfolio is reduced to 10.45%. Thus, the net gain (or loss) on the portfolio is significantly reliant on the EURUSD exchange-rate.
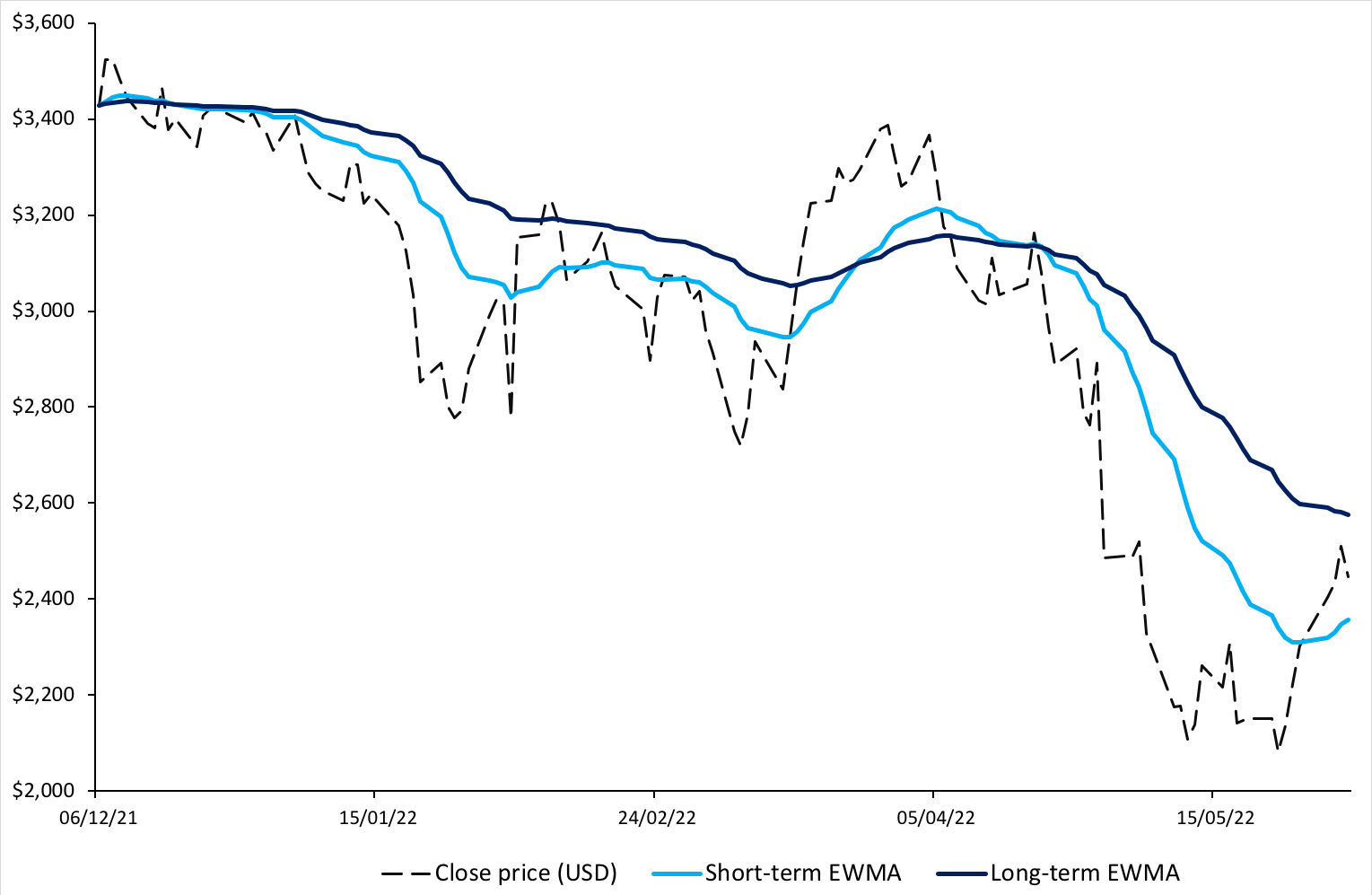
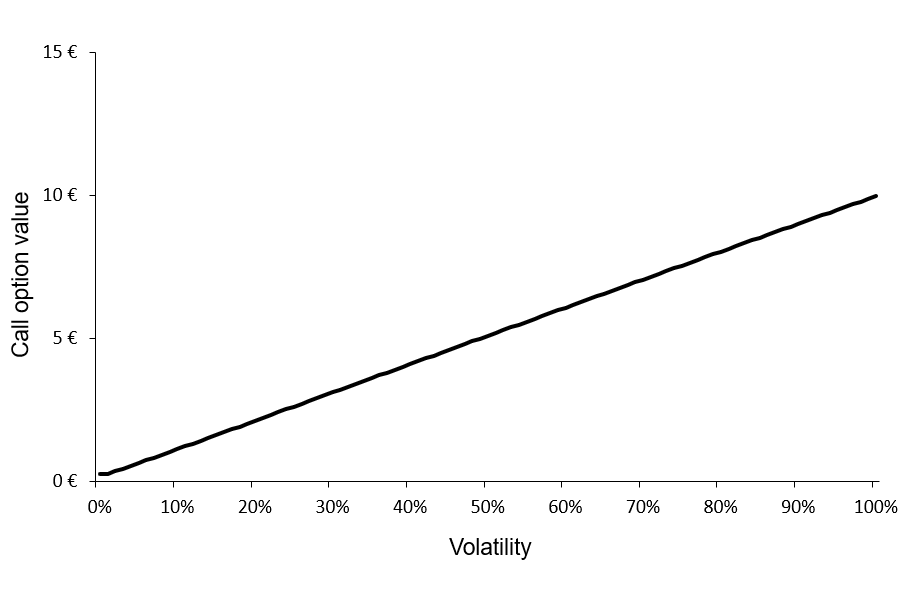
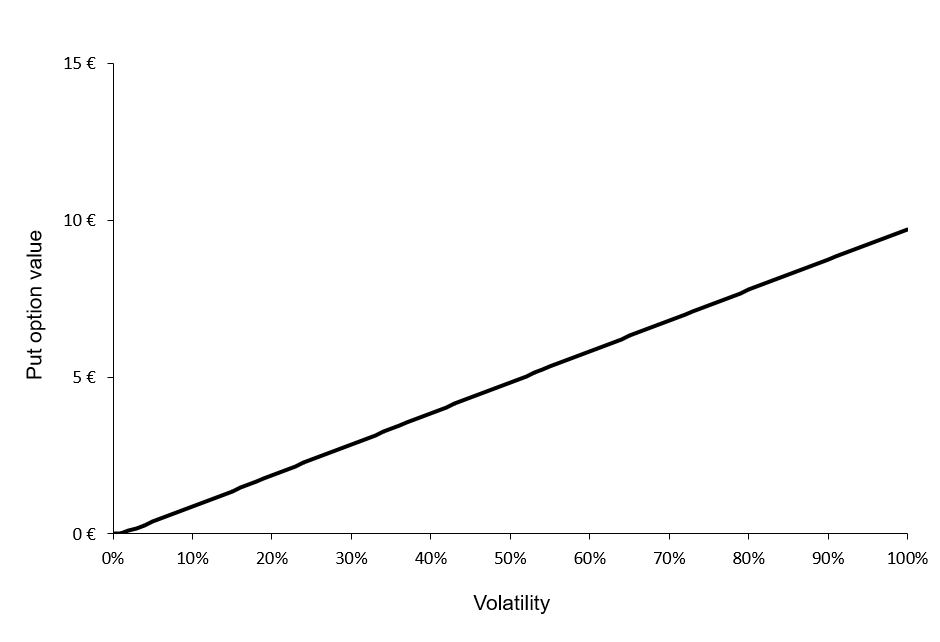
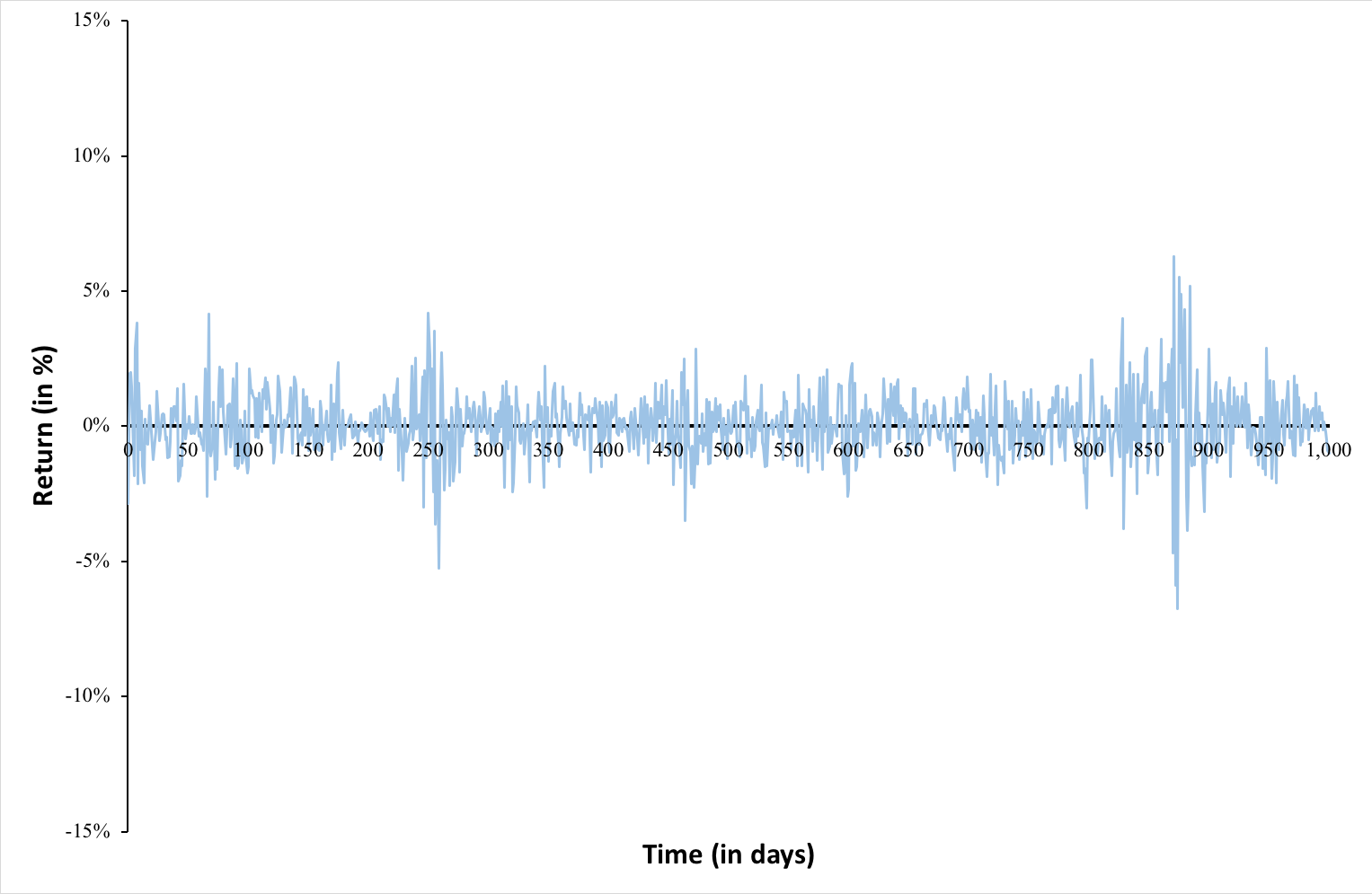
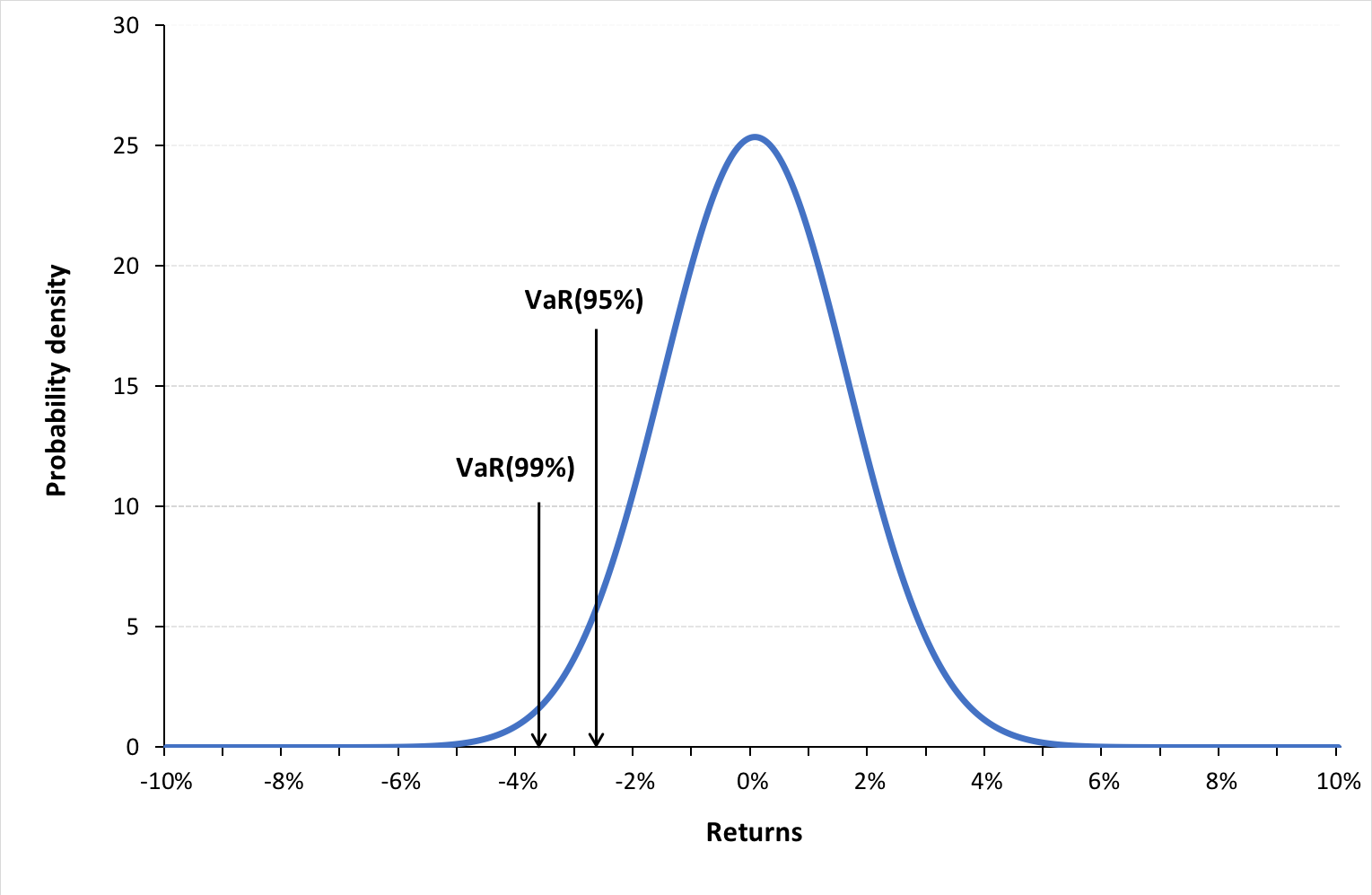
Figure 1 below represents the hedged an unhedged returns on the CAC 40 index. The difference between the two returns illustrates the currency risk for an unhedged position of an investor in the US on a foreign equity market (the French equity market represented by the CAC 40 index.
Figure 1 Hedged and unhedged returns for a position on the CAC 40 index.
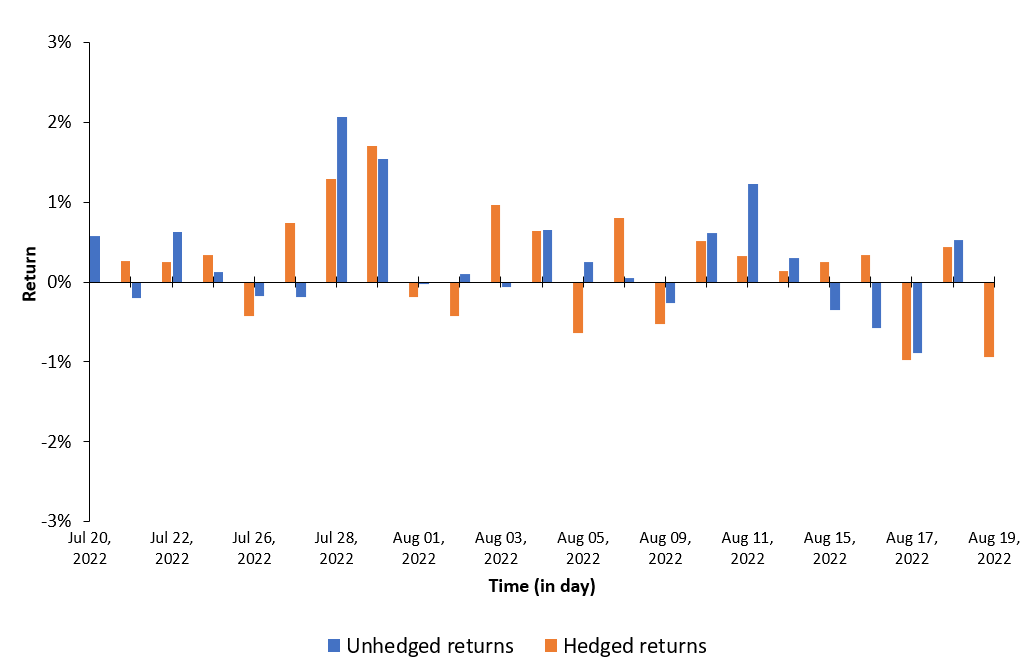 Source : computation by the author.
Source : computation by the author.
Currency overlay is a strategy that is implemented to manage currency exposures by hedging against foreign exchange risk. Currency overlay is typically used by institutional investors like big corporates, asset managers, pension funds, mutual funds, etc. For such investors exchange-rate risk is indeed a concern. Note that institutional investors often outsource the implementation of currency overlays to specialist financial firms (called “overlay managers”) with strong expertise in foreign exchange risk. The asset allocation and the foreign exchange risk management are then separated and done by two different persons (and entities), e.g., the asset manager and the overlay manager. This organization explains the origin of the world “overlay” as the foreign exchange risk management is a distinct layer in the management of the fund.
Overlay managers make use of derivatives like currency forwards, currency swaps, futures and options. The main idea is to offset the currency exposure embedded in the portfolio assets and providing hedged returns from the international securities. The implementation can include hedging all or a proportion of the currency exposure. Currency overlay strategies can be passive or active depending on portfolio-specific objectives, risk-appetite of investors and currency movement viewpoint.
Types of currency overlay strategies
Active currency overlay
Active currency overlay focuses on not just hedging the currency exposure, but also profiting additionally from exchange-rate movements. Investors keeps a part of their portfolio unhedged and take up speculative positions based on their viewpoint regarding the currency trends.
Passive currency overlay
A passive overlay focuses only on hedging the currency exposure to mitigate exchange-rate risk. Passive overlay is implemented through derivative contracts like currency forwards which are used to lock-in a specific exchange-rate for a fixed time-period, thus providing stability to asset values and protection against exchange-rate fluctuations.
Passive overlay is a simple strategy to implement and generally uses standardized contracts, however, it also eliminates the scope of generating any additional profits for the portfolio through exchange-rate fluctuations.
Implementing currency overlays
Base currency and benchmark
Base currency is generally the currency in which the portfolio is dominated or the investor’s domestic currency. A meaningful benchmark selection is also essential to analyze the performance and assess risk of the overlay. World market indices such as those published by MSCI, FTSE, S&P, etc. can be appropriate choices.
Hedge ratio
Establishing a strategic hedge ratio is a fundamental step in implementing a currency overlay strategy. It is the ratio of targeted exposure to be currency hedged by the overlay against the overall portfolio position. Different hedge ratios can have different impact on the portfolio returns and determining the optimal hedge ratio can depend on various factors such as investor risk-appetite and objectives, portfolio assets, benchmark selection, time horizon for hedging etc.
Cost of overlay
The focus of overlays is to hedge the fluctuations in foreign exchange rates by generating cashflows to offset the foreign exchange rate movements through derivatives like currency forwards, currency swaps, futures and options. The use of these derivatives products generates additional costs that impacts the overall performance of the portfolio strategy. These costs must be compared to the benefits of portfolio volatility reduction coming from the overlay implementation.
This cost is also an essential factor in the selection of the hedge ratio.
Note that passive overlays are generally cheaper than active overlays in terms of implementation costs.
Related posts on the SimTrade blog
▶ Jayati WALIA Credit risk
▶ Jayati WALIA Fixed income products
▶ Jayati WALIA Plain Vanilla Options
▶ Akshit GUPTA Currency swaps
Useful resources
Academic articles
Black, F. (1989) Optimising Currency Risk and Reward in International Equity Portfolios. Financial Analysts Journal, 45, 16-22.
Business material
Pensions and Lifetime Savings Association Currency overlay: why and how? video.
About the author
The article was written in September 2022 by Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).



 Source: www.advratings.com
Source: www.advratings.com Source: Amundi
Source: Amundi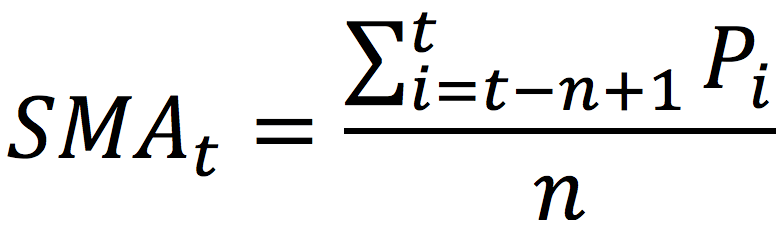
 Source: Computation by author.
Source: Computation by author.