Capital Asset Pricing Model (CAPM)

In this article, Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) presents the Capital Asset Pricing Model (CAPM).

Introduction

The Capital Asset Pricing Model (CAPM) is a widely used metrics for the financial analysis of the performance of stocks. It shows the relationship between the expected return and the systematic risk of investing in an asset. The idea behind the model is that the higher the risk in an investment in securities, the higher the returns an investor should expect on his/her investments.

The Capital Asset Pricing Model was developed by financial economists William Sharpe, John Lintner, Jack Treynor and Jan Mossin independently in the 1960s. The CAPM is essentially built on the concepts of the Modern Portfolio Theory (MPT), especially the mean-variance analysis model by Harry Markowitz (1952).

CAPM is very often used in the finance industry to calculate the cost of equity or expected returns from a security which is essentially the discount rate. It is an important tool to compute the Weighted Average Cost of Capital (WACC). The discount rate is then used to ascertain the Present Value (PV) and Net Present Value (NPV) of any business or financial investment.

CAPM formula

The main result of the CAPM is a simple mathematical formula that links the expected return of an asset to its risk measured by the beta of the asset:

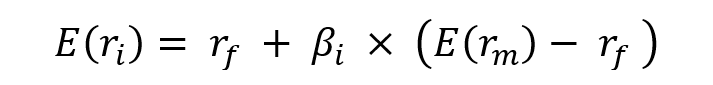
Where:

• E(r_i) represents the expected return of asset i
• r_f the risk-free rate
• β_i the measure of the risk of asset i
• E(r_m) the expected return of the market
• E(r_m)- r_f the market risk premium.

The risk premium for asset i is equal to β_i(E(r_m)- r_f), that is the beta of asset i, β_i, multiplied by the risk premium for the market, E(r_m)- r_f.

The formula shows that investors demand a return higher than the risk-free rate for taking higher risk. The equity risk premium is the component that reflects the excess return investors require on their investment.

Let us discuss the components of the Capital Asset Pricing Model individually:

Expected return of the asset: E(r_i)

The expected return of the asset is essentially the minimum return that the investor should demand when investing his/her money in the asset. It can also be considered as the discount rate the investor can utilize to ascertain the value of the asset.

Risk-free interest rate: r_f

The risk-free interest rate is usually taken as the yield on debt issued by the government (the 3-month Treasury bills and the 10-year Treasury bonds in the US) as they are the safest investments. As government bonds have very rare chances of default, their interest rates are considered risk-free.

Beta: β

The beta is a measure of the systematic or the non-diversifiable risk of an asset. This essentially means the sensitivity of an asset price compared to the overall market. The market beta is equal to 1. A beta greater than 1 for an asset signifies that the asset is riskier compared to the overall market, and a beta of less than 1 signifies that the asset is less risky compared to the overall market.

The beta is calculated by using the equation:

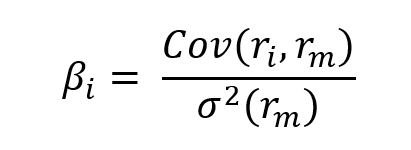
Where:

• Cov(r_i, r_m) represents the covariance of the return of asset i with the return of the market
• σ²(r_m) the variance of the return of the market.

The beta of an asset is defined as the ratio of the covariance between the asset return and the market return, and the variance of the market return.

The covariance is a measure of correlation between two random variables. In practice, the covariance is calculated using historical data for the asset return and the market return.

The variance is a measure of the dispersion of returns. The standard deviation, equal to the square root of the variance, is a measure of the volatility in the market returns over time.

Expected market return

The expected market return is usually computed using historical data of the market. The market is usually represented by a stock index to which the stock belongs to.

For example, for calculating the expected return on APPLE stock, we usually consider the S&P 500 index. Historically, the expected return for the S&P 500 index is around 9%.

Assumptions in Capital Asset Pricing Model

The CAPM considers the following assumptions which forms the basis for the model:

• Investors are risk averse and rational – In the CAPM, all investors are assumed to be risk averse. They diversify their portfolio which neutralizes the non-systematic or the diversifiable risk. So, in the end only the systematic or the market risk is considered to calculate the expected returns on the security.
• Efficient markets – The markets are assumed to be efficient, thus all investors have equal access to the same information. Also, all the assets are considered to be liquid, and an individual investor cannot influence the future prices of an asset.
• No transaction costs – The CAPM assumes that there are no transaction costs, taxes, and restrictions on borrowing or lending activities.
• Risk premium – The CAPM model assumes that investors require higher premium for more risk they take (risk aversion).

Example

As an example, lest us consider an investor who wants to calculate the expected return on an investment in APPLE stock. Let’s see how the CAPM can be used in this case.

The risk-free interest rate is taken to be the current yield on 10-year US Treasury bonds. Let us assume that its value is 3%.

The S&P 500 index has an expected return of 9%.

The beta on APPLE stock is 1.25.

The expected return on APPLE stock is equal to 3% + 1.25*(9% – 3%) = 10.50%

Related posts on the SimTrade blog

   ▶ Youssef LOURAOUI Beta

   ▶ Youssef LOURAOUI Markowitz Modern Portfolio Theory

   ▶ Youssef LOURAOUI Capital Market Line (CML)

   ▶ Youssef LOURAOUI Security Market Line (SML)

   ▶ Akshit GUPTA Asset Allocation

   ▶ Jayati WALIA Linear Regression

Useful resources

Acadedmic articles

Lintner, J. (1965) The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets The Review of Economics and Statistics 47(1) 13-37.

Markowitz, H. (1952) Portfolio Selection The Journal of Finance 7(1) 77-91.

Mossin, J. (1966) Equilibrium in a Capital Asset Market Econometrica 34(4) 768-783.

Merton, R.C. (1973) An Intertemporal Capital Asset Pricing Model Econometrica 41(5) 867-887.

Sharpe, W.F. (1964) Capital Asset Prices: A Theory of Market Equilibrium Under Conditions of Risk The Journal of Finance 19(3) 425-442.

Business sources

Mullins, D.W. Jr (1982) Does the Capital Asset Pricing Model Work? Harvard Business Review.

About the author

The article was written in September 2021 by Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).