Complexité sur les marchés financiers
Je souhaitais vous faire part de ma dernière publication Complexité sur les marchés financiers publiée dans l’ouvrage collectif Complexité et Organisations édité par Edgar Morin et Laurent Bibard, et publié aux Editions Eyrolles. Cette publication résulte des travaux de recherche menée au sein de la Chaire Edgar Morin de la complexité à l’ESSEC Business School.
Comment appréhender la complexité des marchés financiers ? Cette contribution présente trois méthodes pour approcher la complexité des marchés financiers : l’approche statistique avec la théorie des valeurs extrêmes, l’approche historique fondée l’études des crises passées et l’approche de simulation.
Les approches statistique et historique permettent à leur manière de dégager des faits stylisés qui se répètent au cours des crises. L’approche de la simulation avec la plateforme SimTrade permet de comprendre en profondeur les décisions financières prises par les individus et les mécanismes des marchés financiers.
L’approche statistique avec la théorie des valeurs extrêmes
La théorie des valeurs extrêmes s’intéresse aux valeurs minimales et maximales d’un processus aléatoire comme le prix des actions cotés sur les marchés financiers (les booms et les krachs).
Selon le poids des queues de distribution, on obtient une loi de Weibull (absence de queue), une loi de Gumbel (queue fine) et une loi de Fréchet (queue épaisse). Ces distributions sont représentées ci-dessous.
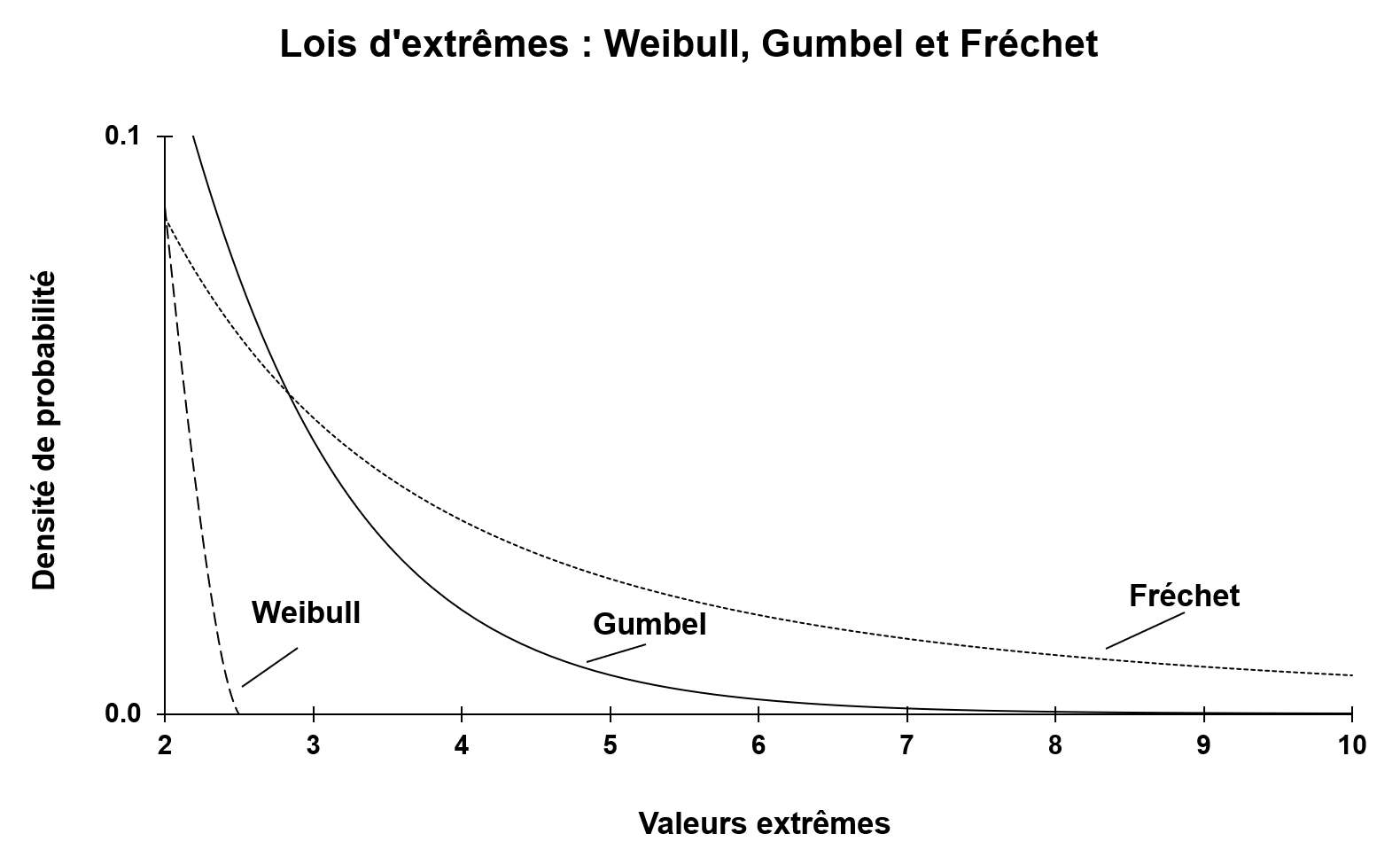
De nombreux travaux académiques ont montré que la théorie des valeurs extrêmes appliquée aux marchés financiers donnait une loi de Fréchet (avec des queues épaises impliquant uen porprtion non négligeable de booms et de krachs). Ces résultats empiriques sont très stables que l’on s’intéresse aux actions individuelles, aux indices d’actions, aux taux de change ou d’intérêt, aux prix des matières premières, etc. Ce résultat est en outre stable au cours du temps ainsi que selon la fréquence utilisée pour mesurer les rentabilités (journalière, hebdomadaire, mensuelle).
L’approche historique avec l’étude des crises passées
Dans son ouvrage Manias, Panics and Crashes : A History of Financial Crises , Charles Kindelberger propose une anatomie des crises financières en cinq étapes : changement, boom, euphorie, crise et répulsion.
- Le changement
L’élément déclencheur de la crise est un changement survenant dans l’environnement, un choc : une innovation technologique, une évolution réglementaire (comme celle qui, dans les années 1920, a permis d’emprunter pour acquérir des actions), un événement politique, etc. Ainsi, la crise de 2007 s’explique par la volonté politique de rendre les Américains propriétaires de leur habitation, associée à une période de taux d’intérêt très faibles et à des innovations financières relatives aux produits structurés de crédit.
- Le boom
La seconde étape, celle du boom, se circonscrit aux professionnels. Elle se traduit par une hausse des prix et un recours élevé au crédit soit pour financer l’économie, soit pour alimenter la spéculation boursière.
- L’euphorie
Dans un troisième temps, le phénomène du boom s’étend au grand public, aux investisseurs individuels. La hausse des prix s’accélère de façon exponentielle. Il devient alors difficile de liquider les positions. A cela s’ajoute un discours médiatique d’un optimisme dépassant la réalité, qui alimente la tendance haussière et renforce son caractère exponentiel.
- La crise
Quand point la crise, les professionnels et les initiés sont les premiers à vendre leurs positions. Puis un événement déclencheur, pouvant être mineur, affecte la confiance et induit un renversement des anticipations. S’ensuit une vague de vente panique par les spéculateurs et les investisseurs individuels, corrélée à une absence totale de liquidité.
- La répulsion
Une étape de répulsion survient enfin, les médias relayant cette fois un discours négatif et recherchant des coupables (songeons à Bernard Madoff pour la crise de 2007-2008). Pour éviter un effondrement de l’économie, les forces centrales interviennent comme prêteurs en dernier ressort.
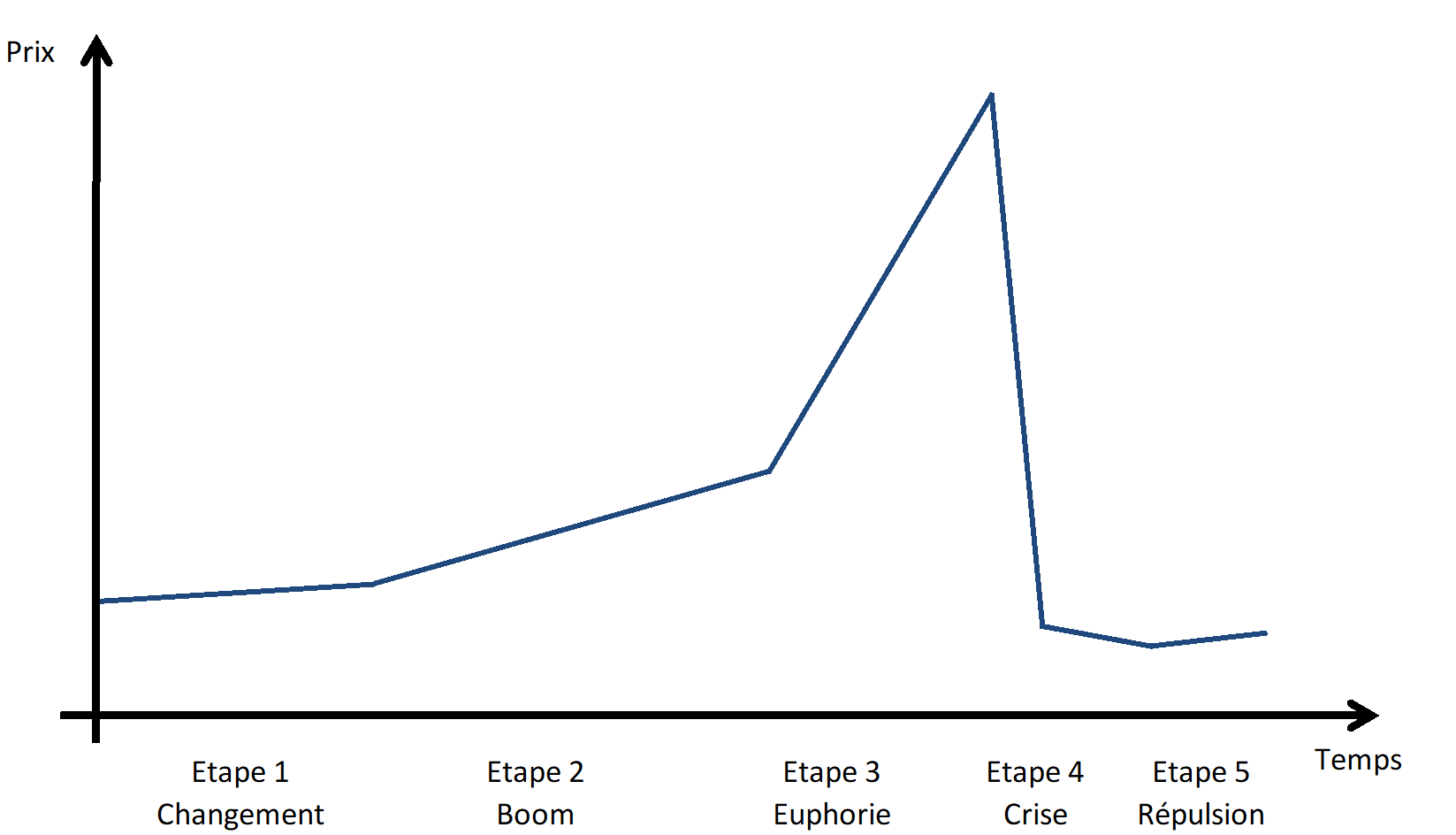
L’approche de simulation
Au-delà des approches historique et statistique, j’ai contribué à l’élaboration d’une troisième approche qui, en s’appuyant sur des simulations, se propose d’entrer dans une compréhension profonde des phénomènes financiers. Elle prend forme dans l’outil pédagogique SimTrade.
Avec les simulations, SimTrade permet de vivre en quelques minutes une journée de trading sur les marchés financiers. L’internaute-trader (« le SimTrader ») dispose d’une plateforme de trading pour acheter et vendre des actions, et un modèle mathématico-financier simule de façon réaliste le comportement des autres traders avec lesquels il échange. Les entreprises émettrices d’actions sont également simulées, les événements qu’elles traversent ayant un impact sur les marchés. SimTrade tire son originalité de la simulation complète qu’il propose, recouvrant aussi bien les marchés que les entreprises. Il se distingue en cela des autres outils de simulation, incomplets, où les ordres sont fictifs mais portent sur les actions d’entreprises bien réelles. Dans ces outils, les ordres n’ont d’impact sur les marchés. C’est au contraire le cas avec SimTrade.
SimTrade a été modélisé pour tenir compte de la complexité des marchés financiers, ces derniers étant des lieux de rencontres physiques ou virtuels entre acheteurs et vendeurs. La modélisation de l’activité des traders intègre leurs motivations (un besoin de liquidité, une réactivité à l’information économique ou financière…) et leurs stratégies, ainsi que les caractéristiques des ordres. Ces derniers sont agrégés dans une plateforme de trading. Ainsi les transactions se traduisent-elles par des prix et des volumes.
L’algorithme de simulation (dit de Monte Carlo) qu’utilise SimTrade repose sur une suite de nombres dont le premier terme est appelé la « graine » de la simulation. Or — et cela renvoie explicitement à la pensée de la complexité —, une modification minime de cette « graine » peut entraîner une fluctuation des cours de grande ampleur, tel un battement d’ailes de papillon susceptible de déclencher une tornade à l’autre bout du monde. Autre effet de la complexité, le gain d’un trader peut résulter certes de la pertinence de sa stratégie, mais aussi des interventions d’autres traders ayant eu dans le même temps des impacts sur le marché.
Les simulations SimTrade utilisent à la base un générateur de nombres aléatoires. Ces nombres aléatoires sont par exemple utilisés pour simuler le nombre d’ordres passés par les SimTraders ainsi que les différents paramètres de ces ordres (sens, quantité, type, etc.).
Techniquement, le générateur de nombres aléatoires utilisé repose sur un algorithme linéaire congruentiel :
Un = a✕Un-1 + b (mod m)
Cette relation de récurrence permet de calculer U1 à partir de U0, puis U2 à partir de U1, … et Un à partir de Un-1.
Le terme initial, U0, n’est pas calculé mais choisi. Ce terme initial est appelé la graine (seed en anglais).
Le paramètre a est un coefficient multiplicatif, le paramètre b est un coefficient additif et le paramètre m est le modulo. Pour rappel, l’opération mod donne le reste de la division euclidienne d’un nombre entier par un autre. Par exemple, 13 mod (5) est égal à 3 car 13 = 2✕5 + 3.
Considérons un générateur de nombres aléatoires congruentiel défini par le jeu de paramètres suivant : a = 10, b = 37, m = 251 et U0 = 17.
Un = 10✕Un-1 + 37 (mod 251)
Le tableau ci-dessous détaille le calcul des cinq premiers nombres simulés.
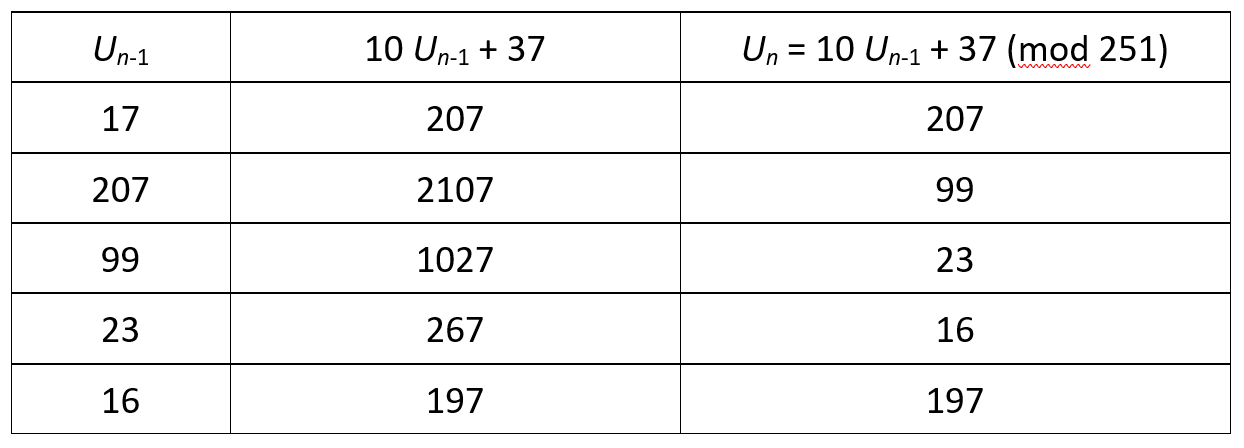
Les générateurs de nombres aléatoires utilisés en pratique utilisent des nombres plus grands pour a, b et m. Quelques jeux de paramètres courants :
a = 1664525, b = 1013904223 et m = 232
a = 31167285, b = 0 et m = 248
Les nombres aléatoires U0, U1, U2, …, Un-1, Un sont compris entre 0 et m-1. Utilisés dans le cadre d’un modèle, ces nombres aléatoires sont ensuite transformés pour être compris entre 0 et 1 (division par m-1) et correspondre ainsi à des nombres aléatoires tirés d’une loi uniforme sur l’intervalle [0, 1].
Exemple
Pour simuler les ordres d’un trader, il faut notamment simuler le sens de cet ordre : achat ou vente. On supposera que l’on souhaite que le trader achète dans 40% des cas et qu’il vende dans 60% des cas. Pour cela, on simule d’abord un nombre entre 0 et m-1 avec le générateur congruentiel. Disons que l’on obtient 37 et que m est égal à 251. Puis, on transforme cet entier en un nombre compris entre 0 et 1. On obtient 0.148 (=37/250). Si ce nombre est inférieur à 0.40, alors on décidera que le sens de l’ordre simulé est l’achat (ce sera bien le cas dans 40% des cas). Si ce nombre est supérieur à 0.40, alors le sens de l’ordre est la vente (ce sera bien le cas dans 60% des cas). Comme 0.148 est inférieure à 0.4, l’ordre simulé sera donc un ordre d’achat.
Illustration de la complexité des marchés
Les figures ci-dessous représentent l’évolution du marché pour la simulation Passer un ordre obtenue en faisant légèrement varier la graine de l’algorithme de simulation : U0 = 122, U0 = 123 et U0 = 124 (un simple battement d’ailes de papillon).
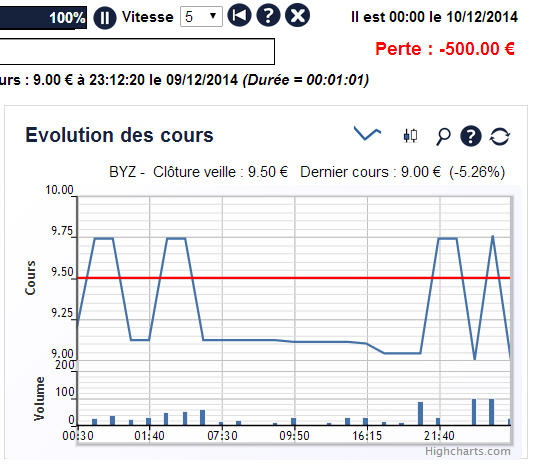
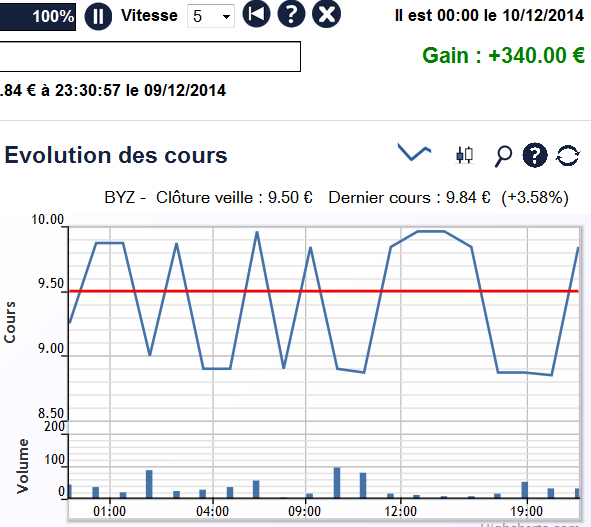
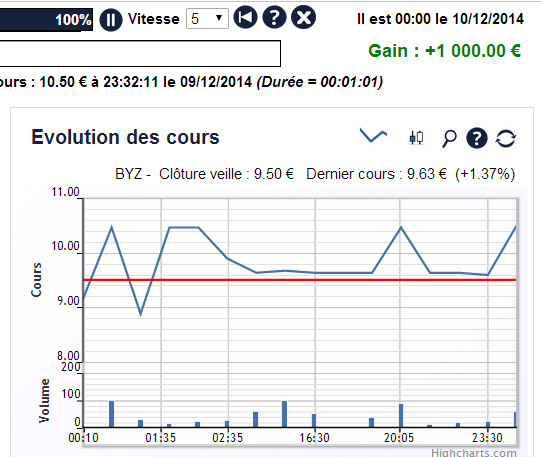
On observe qu’en faisant légèrement varier la graine de l’algorithme de simulation utilisé pour simuler le marché, l’évolution du marché pendant la journée de trading varie fortement. Le cours de bourse et le volume de transaction est très différent d’une simulation à l’autre.


