In this article, Youssef LOURAOUI (Bayes Business School, MSc. Energy, Trade & Finance, 2021-2022) explains how to implement the Markowitz asset allocation model. This model is used to determine optimal asset portfolios based on the risk-return trade-off.
This article follows the following structure: first, we introduce the Markowitz model. We then present the mathematical foundations of this model. We conclude with an explanation of the methodology to build the spreadsheet with the results obtained. You will find in this post an Excel spreadsheet which implements the Markowitz asset allocation model.
Introduction
Markowitz’s work is widely regarded as a pioneer work in financial economics and corporate finance due to its theoretical foundations and applicability in the financial sector. Harry Markowitz received the Nobel Prize in 1990 for his contributions to these disciplines, which he outlined in his 1952 article “Portfolio Selection” published in The Journal of Finance. His major work established the foundation for what is now commonly referred to as “Modern Portfolio Theory” (MPT).
To find the portfolio’s minimal variance, the Markowitz model uses a constrained optimization strategy. The goal of the Markowitz model is to take into account the expected return and volatility of the assets in the investable universe to provide an optimal weight vector that indicates the best allocation for a given level of expected return or the best allocation for a given level of volatility. The expected return, volatility (standard deviation of expected return), and the variance-covariance matrix to reflect the co-movement of each asset in the overall portfolio design are the major inputs for this portfolio allocation model for an n-asset portfolio. We’ll go over how to use this complex method to find the best portfolio weights in the next sections.
Mathematical foundations
The investment universe is composed of N assets characterized by their expected returns μ and variance-covariance matrix V. For a given level of expected return μP, the Markowitz model gives the composition of the optimal portfolio. The vector of weights of the optimal portfolio is given by the following formula:
With the following notations:
- wP = vector of asset weights of the portfolio
- μP = desired level of expected return
- e = identity vector
- μ = vector of expected returns
- V = variance-covariance matrix of returns
- V-1 = inverse of the variance-covariance matrix
- t = transpose operation for vectors and matrices
A, B and C are intermediate parameters computed below:
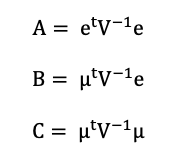
The variance of the optimal portfolio is computed as follows
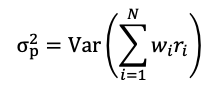
To calculate the standard deviation of the optimal portfolio, we take the square root of the variance.
Implementation of the Markowitz asset allocation model in practice
We generated a large time series to obtain useful results by downloading the equivalent of 23 years of market data from a data provider (in this example, Bloomberg). We generate the variance-covariance matrix after obtaining all necessary statistical data, which includes the expected return and volatility indicated by the standard deviation of the returns for each stock during the provided period. Table 1 depicts the expected return and volatility for each stock retained in this analysis.
Table 1. Asset characteristics of Apple, Amazon, Microsoft, Goldman Sachs, and Pfizer.
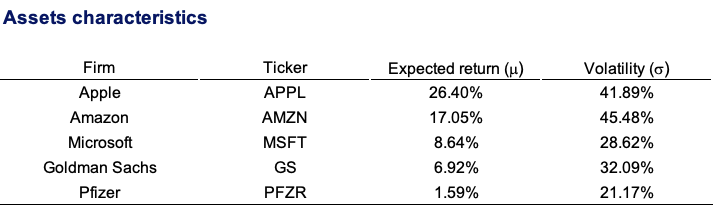
Source: computation by the author.
We use the data analysis tool pack supplied in Excel to run a variance-covariance matrix for ease of computation (Table 2).
Table 2. Variance-covariance matrix of asset returns.

Source: computation by the author.
We can start the optimization task by setting a desirable expected return after computing the expected return, volatility, and the variance-covariance matrix of expected return. With the data that is fed into the appropriate cells, the model will complete the optimization task. For a 10% desired expected return, we get the following results (Table 3).
Table 3. Asset weights for an optimal portfolio.
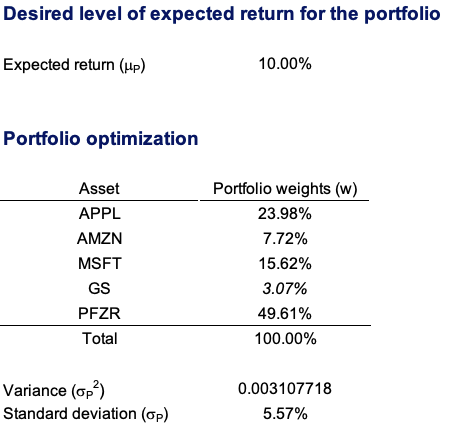
Source: computation by the author.
To demonstrate the effect of diversification in the reduction of volatility, we can form a Markowitz efficient frontier by tilting the desired anticipated return with their relative volatility in a graph. The Markowitz efficient frontier is depicted in Figure 1 for various levels of expected return (Figure 1).
Figure 1. Markowitz efficient portfolio frontier.
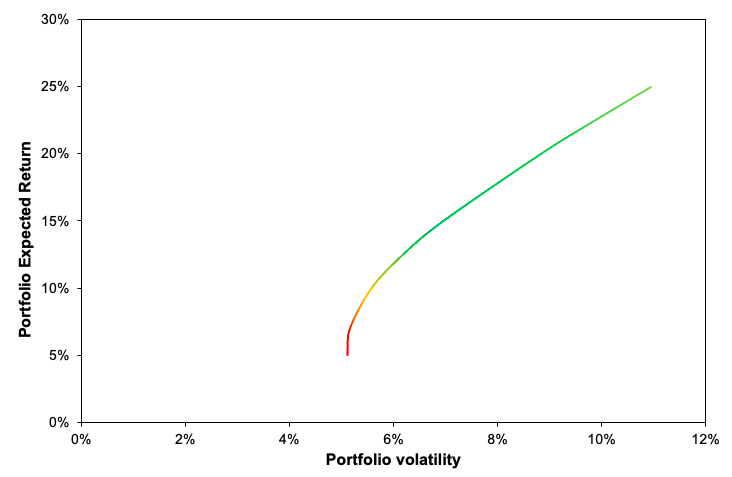
Source: computation by the author.
You can download the Excel file below to use the Markowitz portfolio allocation model.
Why should I be interested in this post?
Modern Portfolio Theory (MPT) is at the heart of modern finance, shaping the modern investing landscape. MPT has become the cornerstone of current financial theory and practice. MPT has been around for nearly sixty years and shows no signs of slowing down. His theoretical contributions paved the way for more portfolio theories. This post helps you to grasp the theoretical model and its implementation.
Related posts on the SimTrade blog
▶ Youssef LOURAOUI Markowitz Modern Portfolio Theory
▶ Youssef LOURAOUI Portfolio
▶ Jayati WALIA Capital Asset Pricing Model (CAPM)
▶ Youssef LOURAOUI Black-Litterman Model
▶ Youssef LOURAOUI Origin of factor investing
▶ Youssef LOURAOUI Alpha
▶ Youssef LOURAOUI Factor Investing
Useful resources
Academic research
Petters, A. O., and Dong, X. 2016. An Introduction to Mathematical Finance and Applications. Springer Undergraduate Texts in Mathematics and Technology.
Markowitz, H., 1952. Portfolio Selection. The Journal of Finance, 7(1): 77-91.
About the author
The article was written in Mars 2022 by Youssef LOURAOUI (Bayes Business School, MSc. Energy, Trade & Finance, 2021-2022).


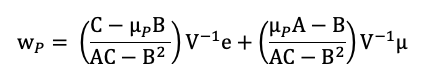

1 thought on “Implementing Markowitz asset allocation model”
Comments are closed.