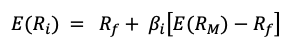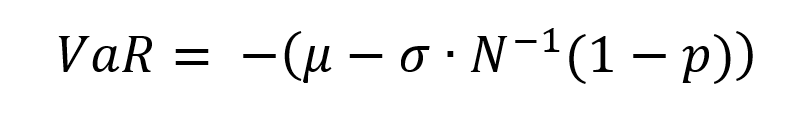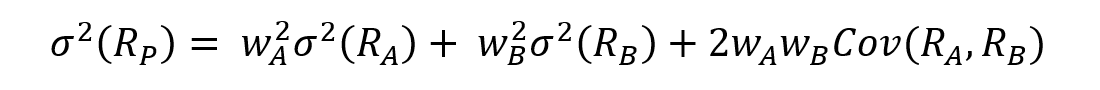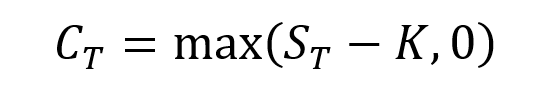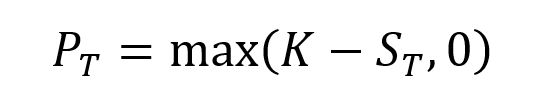Risk comes from not knowing what you are doing
In this article, Michel Henry VERHASSELT (ESSEC Business School – Master in Finance, 2023-2025) comments on a quote by Warren Buffet about risk.
“Risk comes from not knowing what you are doing”
Analysis of the quote
Warren Buffett’s quote, “Risk comes from not knowing what you are doing,” encapsulates a fundamental principle of investing and decision-making. It underscores the significance of knowledge, research, and informed decision-making in managing risk.
One key aspect of this quote is the idea that risk is not solely a result of the inherent uncertainty in investments or ventures. Rather, risk is often the consequence of making decisions without a comprehensive understanding of the situation. In the world of finance and investing, not knowing the intricacies of an investment or the market can lead to hasty, ill-informed choices that carry a higher level of risk.
Moreover, this quote stresses the importance of education and continuous learning in risk management. To minimize risk, individuals need to invest time and effort in gaining knowledge and expertise within their chosen domain. For investors, this means understanding the companies or assets they invest in, analysing financial statements, and staying informed about market trends.
In a broader context, this quote is not limited to finance; it applies to various aspects of life. In personal life just as in business, forgoing the careful analysis of the potential consequences of one’s actions can lead to very negative outcomes. Decisions made in haste, out of anger, excitement, disappointment, and other strong emotions generally tend to be mistakes. Patience and forethought tend to be rewarded.
In essence, Warren Buffett’s quote reminds us that risk is not an abstract force beyond our control. It is, to a significant extent, a product of our knowledge and decisions. By equipping ourselves with information, staying well-informed, and making deliberate choices, we can effectively manage and mitigate risk in both our financial and personal pursuits.
About the author
Warren Buffett is a renowned American investor and CEO of Berkshire Hathaway, known for his value investing approach and philanthropic efforts. His net worth consistently places him among the world’s wealthiest individuals. However, he is equally renowned for his commitment to philanthropy, pledging the majority of his fortune to charitable causes, primarily through the Bill & Melinda Gates Foundation. Buffett’s influence extends far beyond the financial world, making him a respected figure in both business and philanthropy. His life and career continue to inspire countless investors and entrepreneurs worldwide.
Financial concepts related to the quote
Risk management
Of course, the concept most directly related to the quote is risk management. That is perhaps the most fundamental concept of finance. We are dealing with unknowns, probabilities, and expectations. We must make sure that, through careful analysis, we eliminate as much downside potential as possible: that is the only way to guarantee long-term survival (and a fortiori, long-term success). This goal can only be achieved once a thorough understanding is reached of the assets and markets we invest in, and the people we invest or transact with. Without such an understanding, we create unnecessary risk and that will almost assuredly lead to financial losses sooner or later.
Due diligence
The quote underscores the significance of “knowing what you are doing”. In finance, we call this conducting due diligence. It involves comprehensive research and analysis before making any financial commitment. This includes examining a company’s financials, understanding market dynamics, and evaluating potential investments. Without proper due diligence, individuals may enter financial ventures blindly, exposing themselves to significant risks.
Portfolio diversification
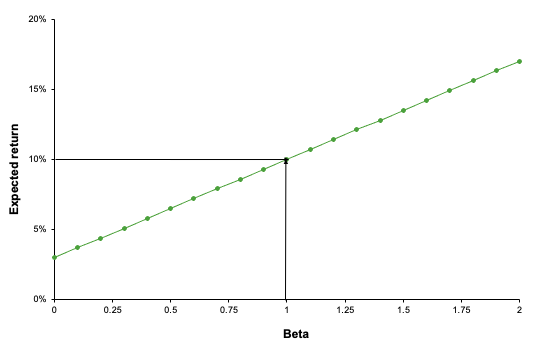
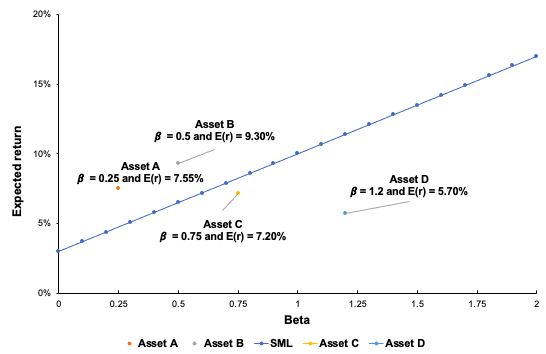
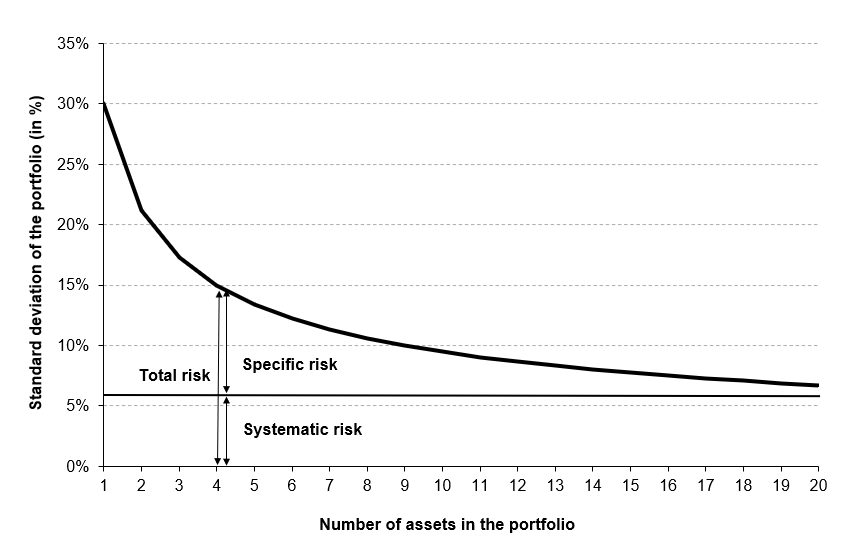
One of the ways in which we mitigate risk is portfolio diversification. When we add assets to our portfolio, we want to reduce or eliminate the risk that comes with exposure to one specific investment, while keeping as much of the return as possible. The concept of beta directly stems from the idea of portfolio diversification. By sticking to a single asset, you are entirely and solely exposed to its volatility; by wholly diversifying your portfolio, you are theoretically reproducing the entire market, making your beta equal to 1, or in other words turning your risk exposure into the market risk. In conclusion, portfolio diversification is a fundamental strategy for risk mitigation in investment, and closely aligns with the quote’s meaning.
My opinion about this quote
In my opinion, Warren Buffett was talking about investing and not trading. However, as my experience and interests are closer to trading than investing, I see it as a useful quote within that context.
Firstly, let’s talk about stop-losses. They’re your safety net. You set them at a certain point where, if the trade goes sour, you bail out. But if you don’t know why you’re placing a stop-loss at a particular level, it’s like playing darts blindfolded. You might hit the target, but it’s mostly luck. Understanding the underlying reasons for your stop-losses is crucial. It’s not just a random number; it’s based on your analysis.
Managing position size is another important element to consider. If you don’t know what you’re doing, you might risk your entire account on a single, promising, trade, much like going all-in on a hand of poker simply because you were dealt a pair of aces. Position sizing is about controlling risk. You need to understand how much you can afford to lose and then adjust your position size accordingly. If you don’t, you’re setting yourself up for potential disaster. It’s important to remember you never know the market, you simply might sometimes guess better than others. Outside of arbitrage or insider trading, certainty does not exist in trading; hence, position size should always be managed intelligently.
Hedging is also related to this quote. A hedge is a plan B. If you are long on a stock, and you are not certain which direction the market will take, you can reduce your risk by creating another position with options or other derivatives. But, if you don’t know how these instruments work or why you’re using them, it’s like having a spare tire but not knowing how to change it. You might end up with two flat tires instead of one.
Lastly, getting an edge on the market. Ultimately this is what every trader claims to be able to do. It boils down, almost entirely, to risk management. You must know your strategy inside out, and you must know exactly what you plan to do if you don’t get this expected edge out of your trade. In this way, over the long run, you can have either a majority of winning trades of equal sizes, or winning trades that outweigh the losing ones in terms of net gain. To have an edge, you need to understand why your approach works, when it might not, and continuously adapt.
In short, in trading and more generally in finance, ignorance isn’t bliss; it’s a one-way ticket to risk.
Why should I be interested in this post?
A finance student should be interested in this post because risk is the single most important concept to understand both in finance and in business. In this post, I believe I have made this concept compelling for students by going beyond theory. My post is also practical. It talks about real-world applications like setting stop-losses, managing position size, and hedging with financial products. These are the tools used daily by finance professionals in capital markets.
Furthermore, finance is all about making sound decisions, and you can’t do that effectively without understanding how to control and mitigate risk. What’s even more interesting is that it clarifies a common misconception. It tells you that gaining an edge in the financial market isn’t about having secret knowledge. It’s understanding your approach and the markets you’re dealing with. Being aware of the importance of risk management is therefore crucial for a wide range of careers and that is why a finance student should take an interest in it.
Related posts on the SimTrade blog
▶ Federico DE ROSSI The Power of Patience: Warren Buffett’s Advice on Investing in the Stock Market
▶ Rayan AKKAWI Warren Buffet and his basket of eggs
▶ Jianen HUANG It’s not whether you’re right or wrong
▶ Clara PINTO Investment is a flighty bird which needs to be controlled
Useful resources
Diversifying your portfolio with a lower net worth
Sharpe’s classic 1964 article on CAPM
About the author
The article was written in December 2023 by Michel Henry VERHASSELT (ESSEC Business School – Master in Finance, 2023-2025).



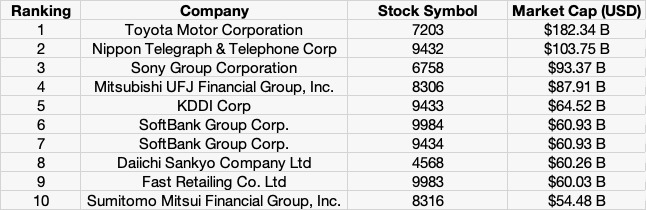
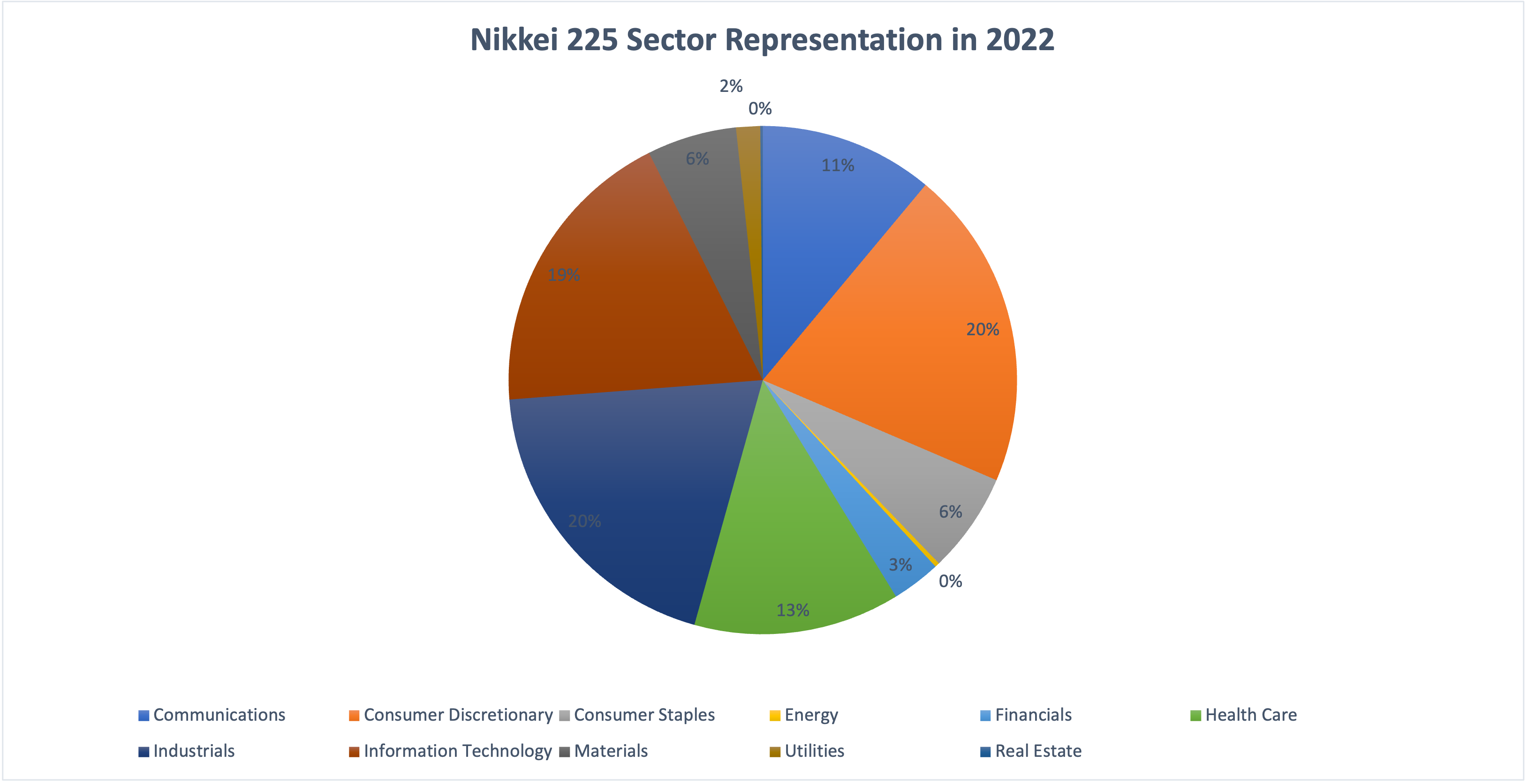
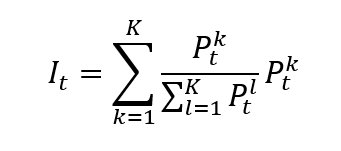
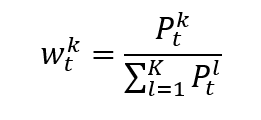
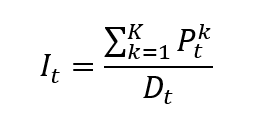

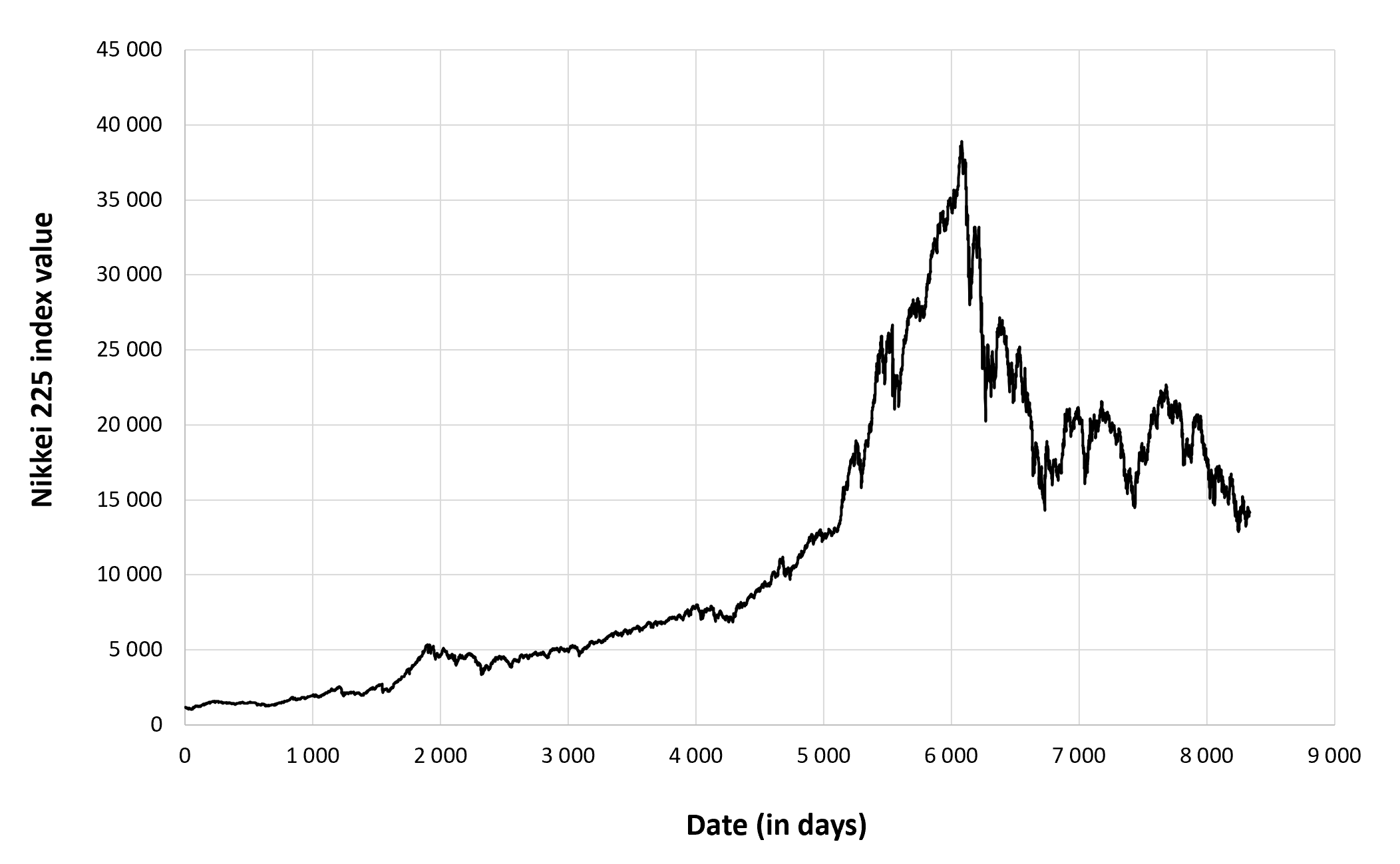
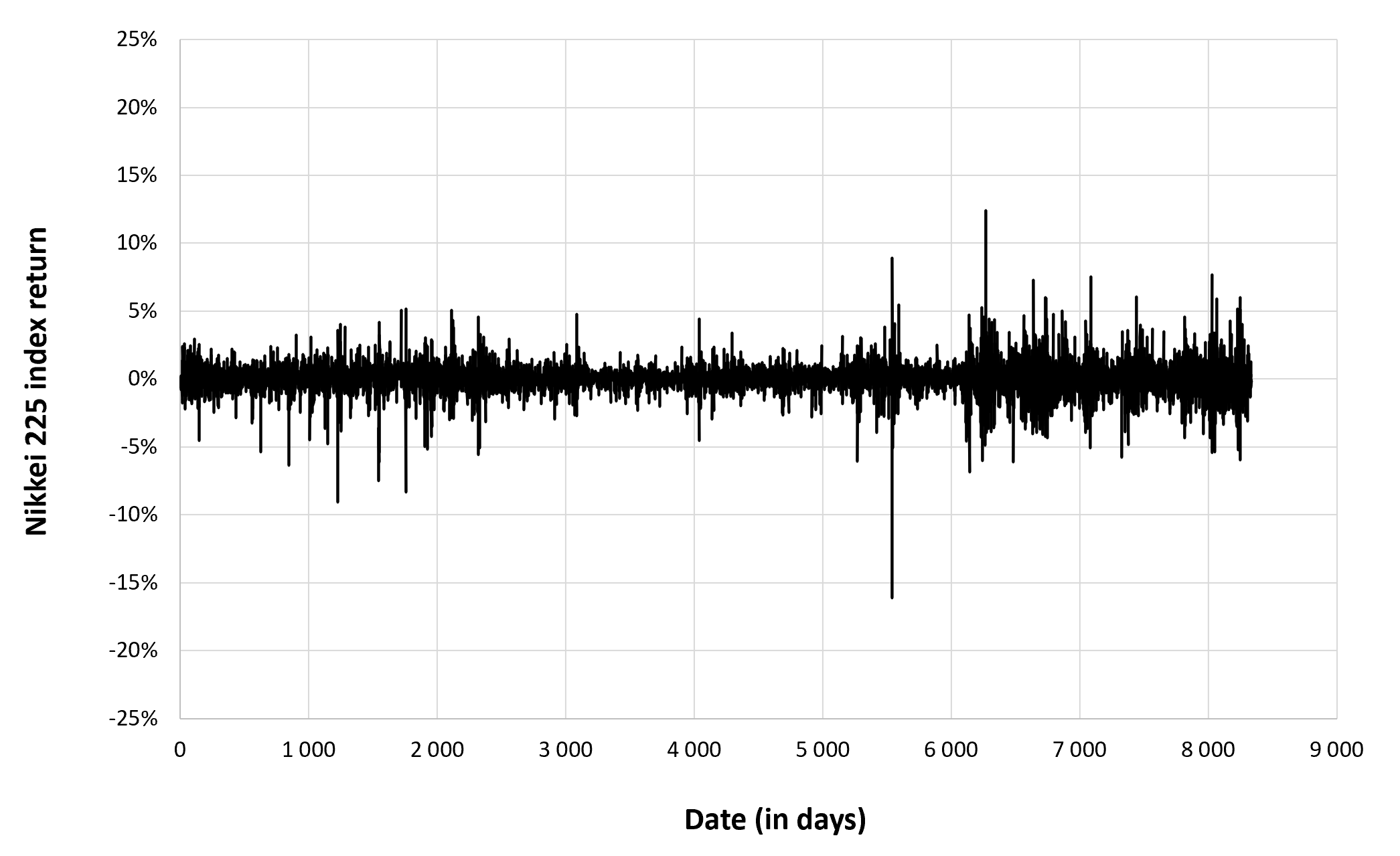
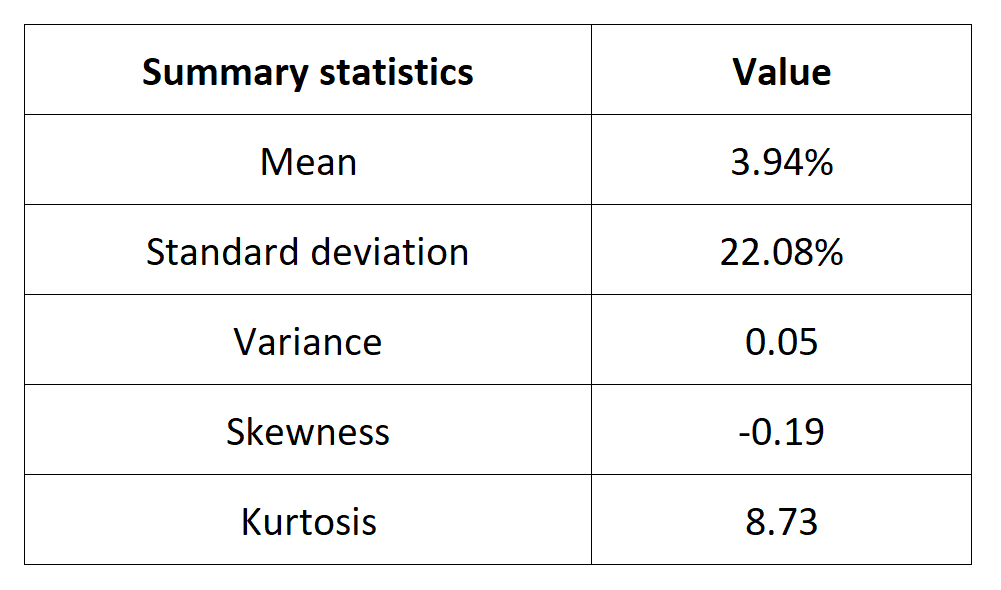
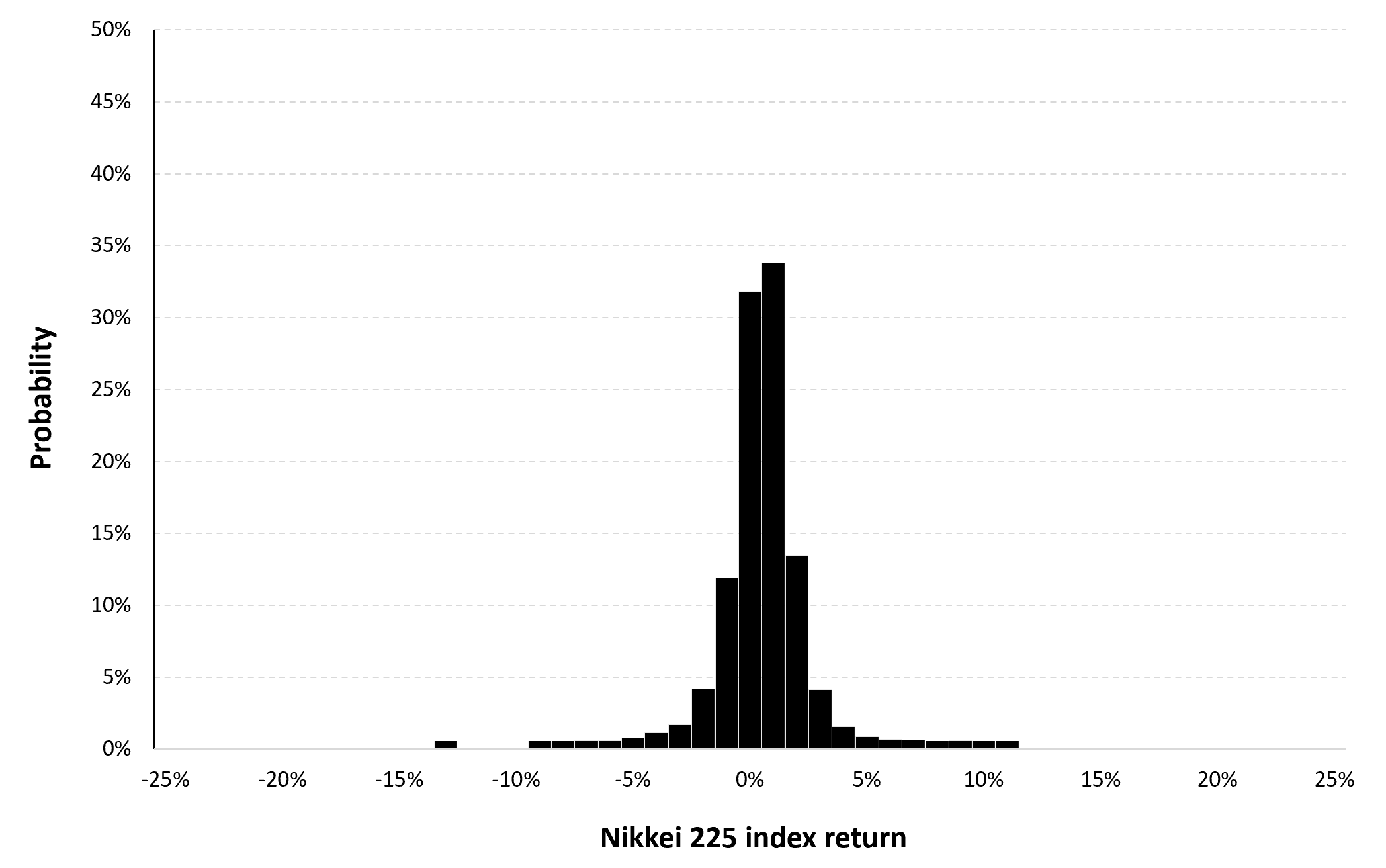
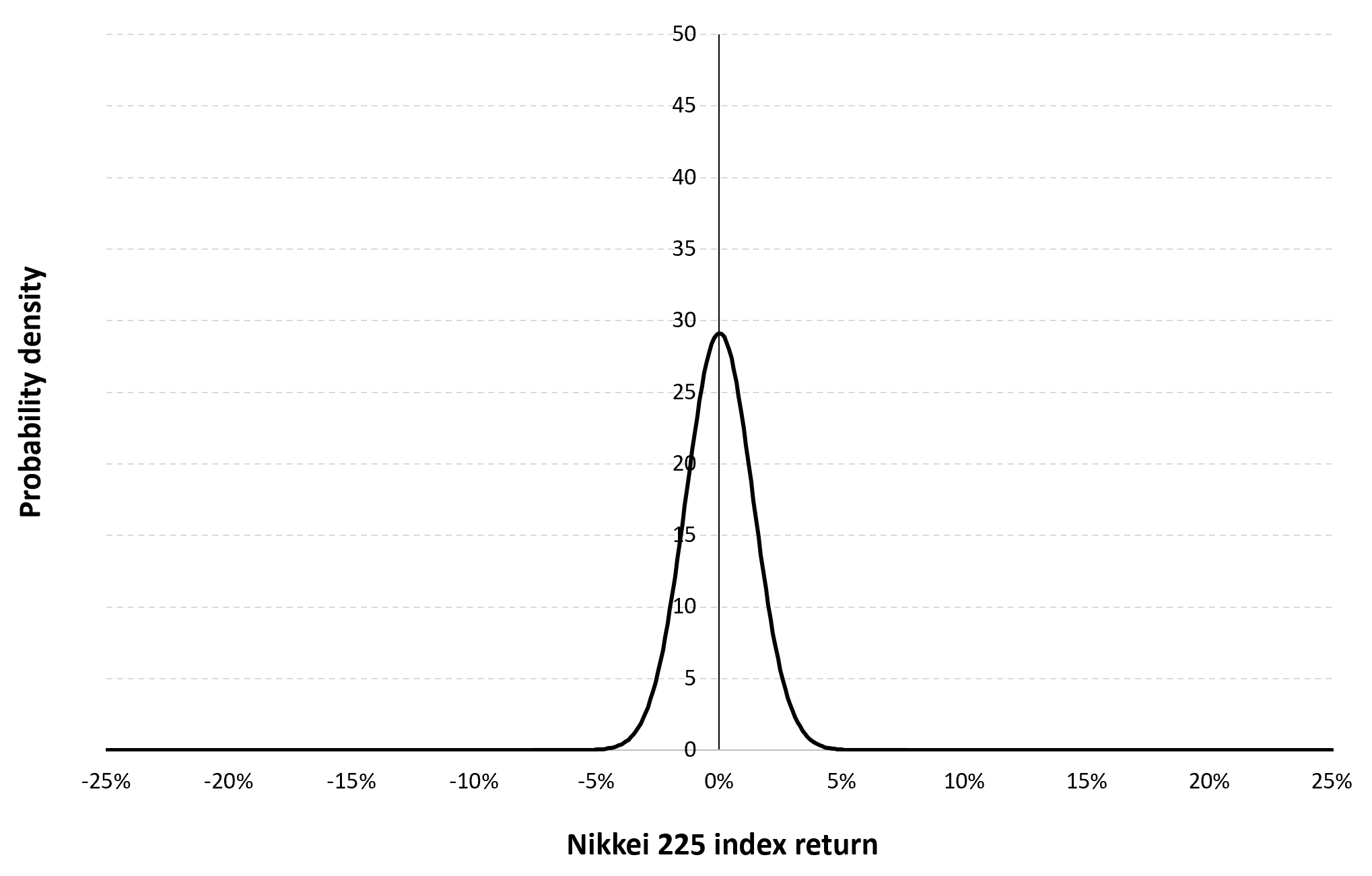
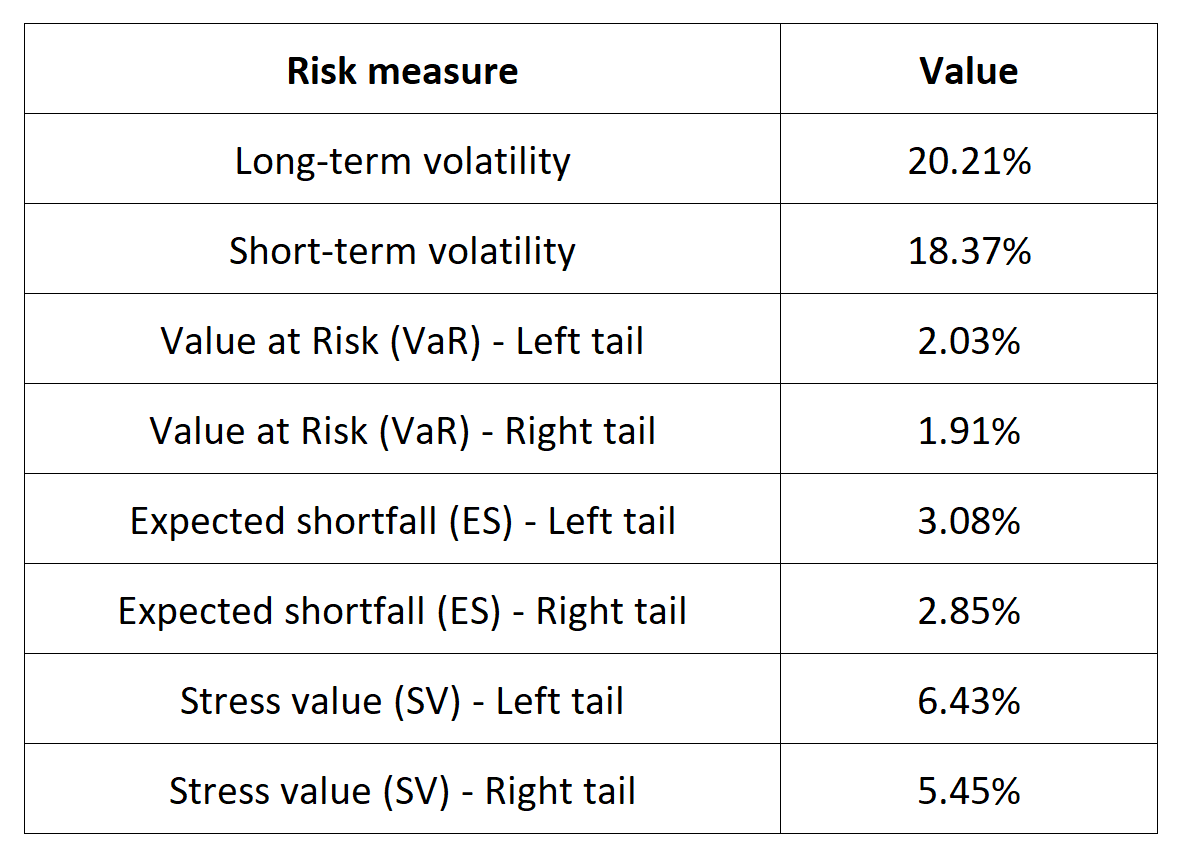
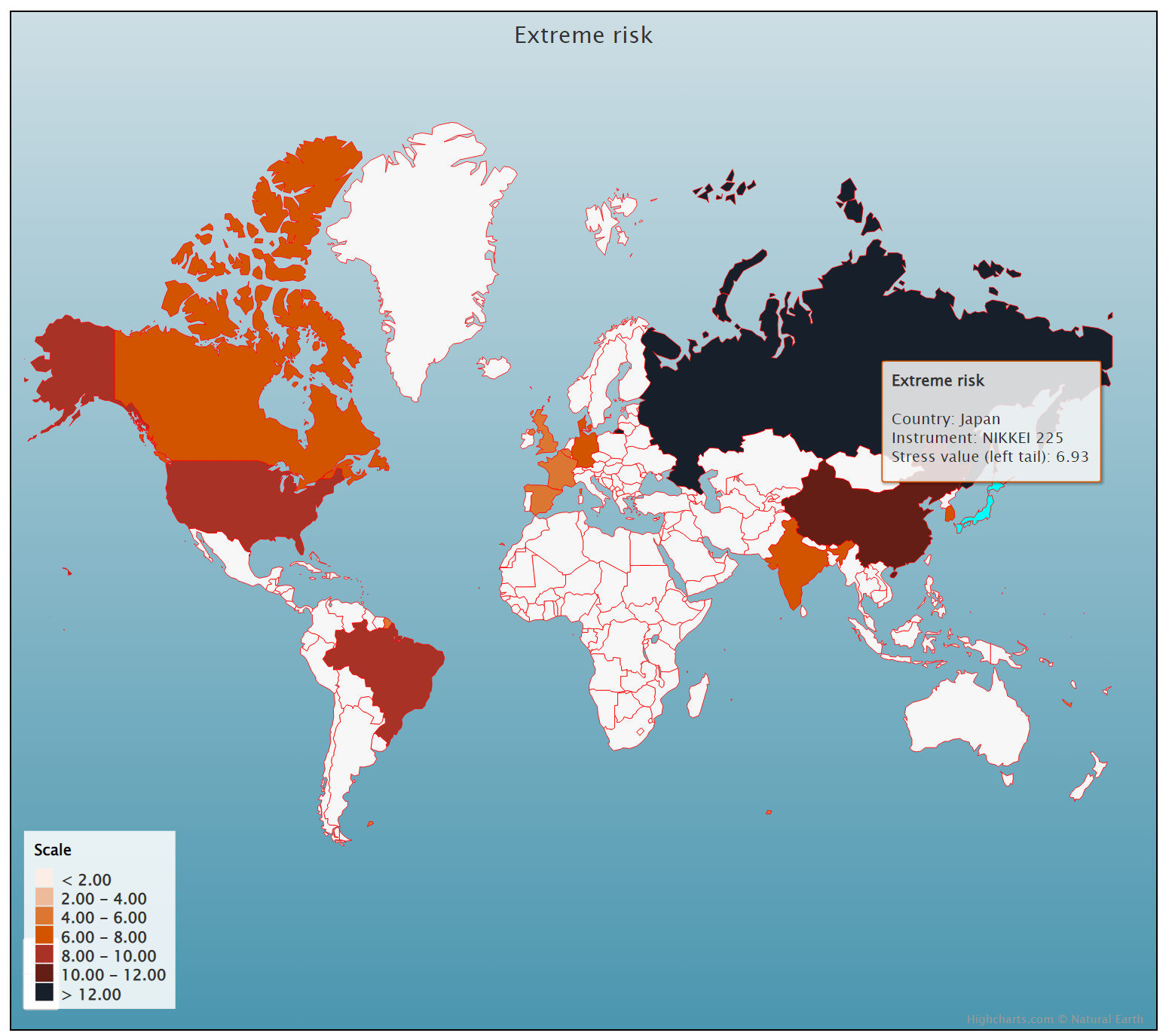

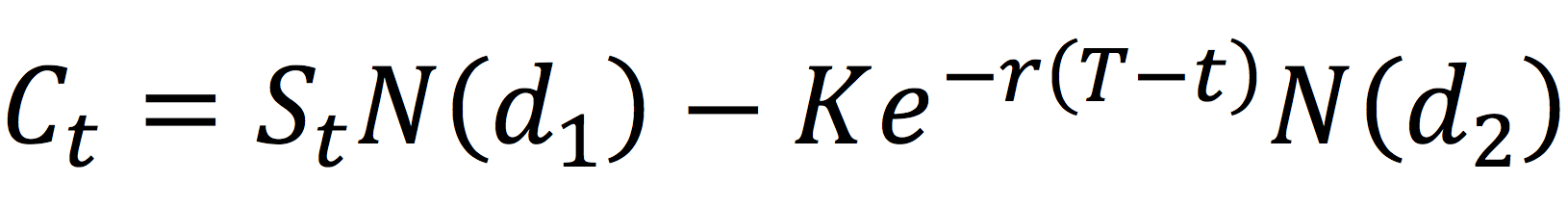
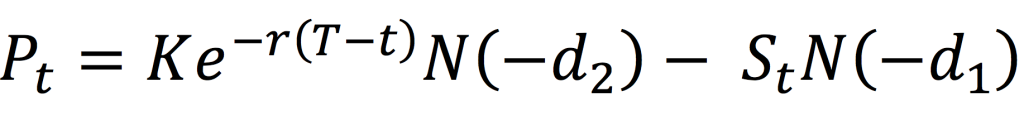
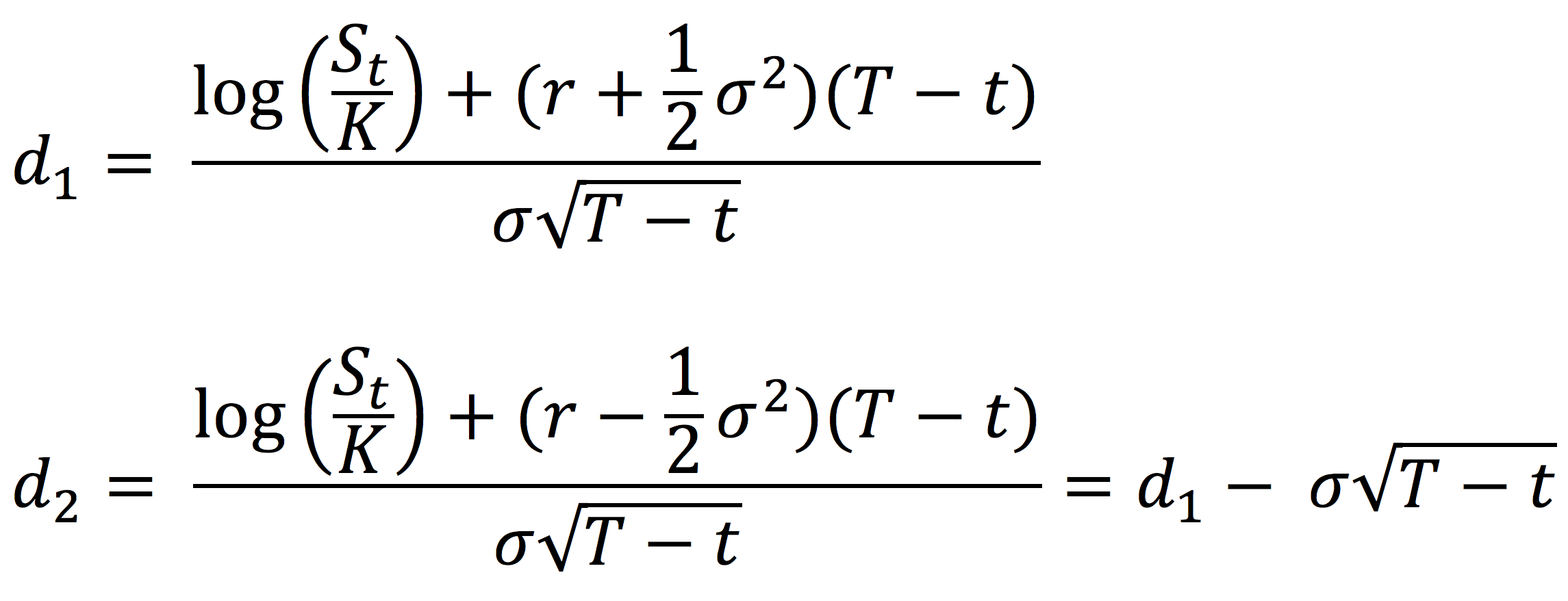
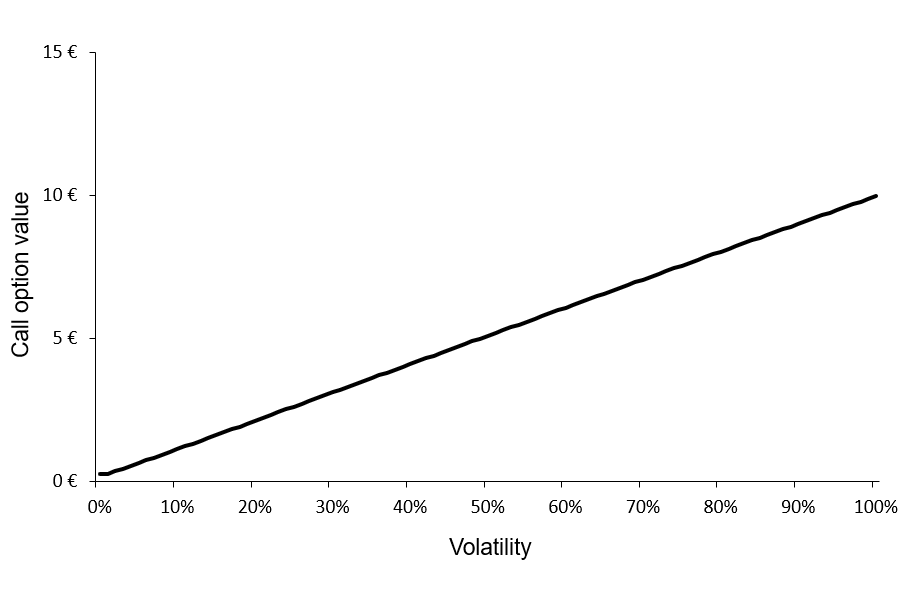
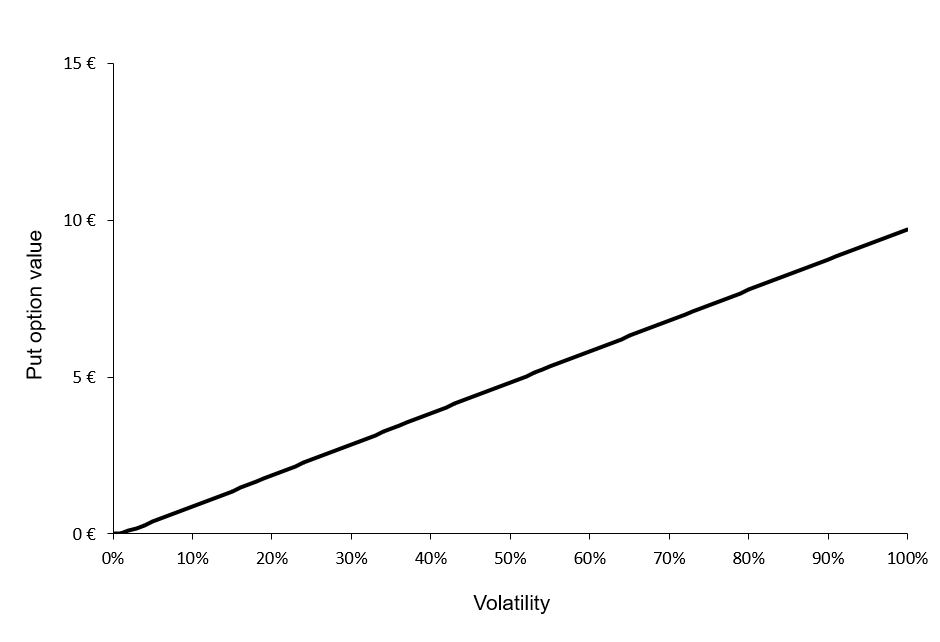

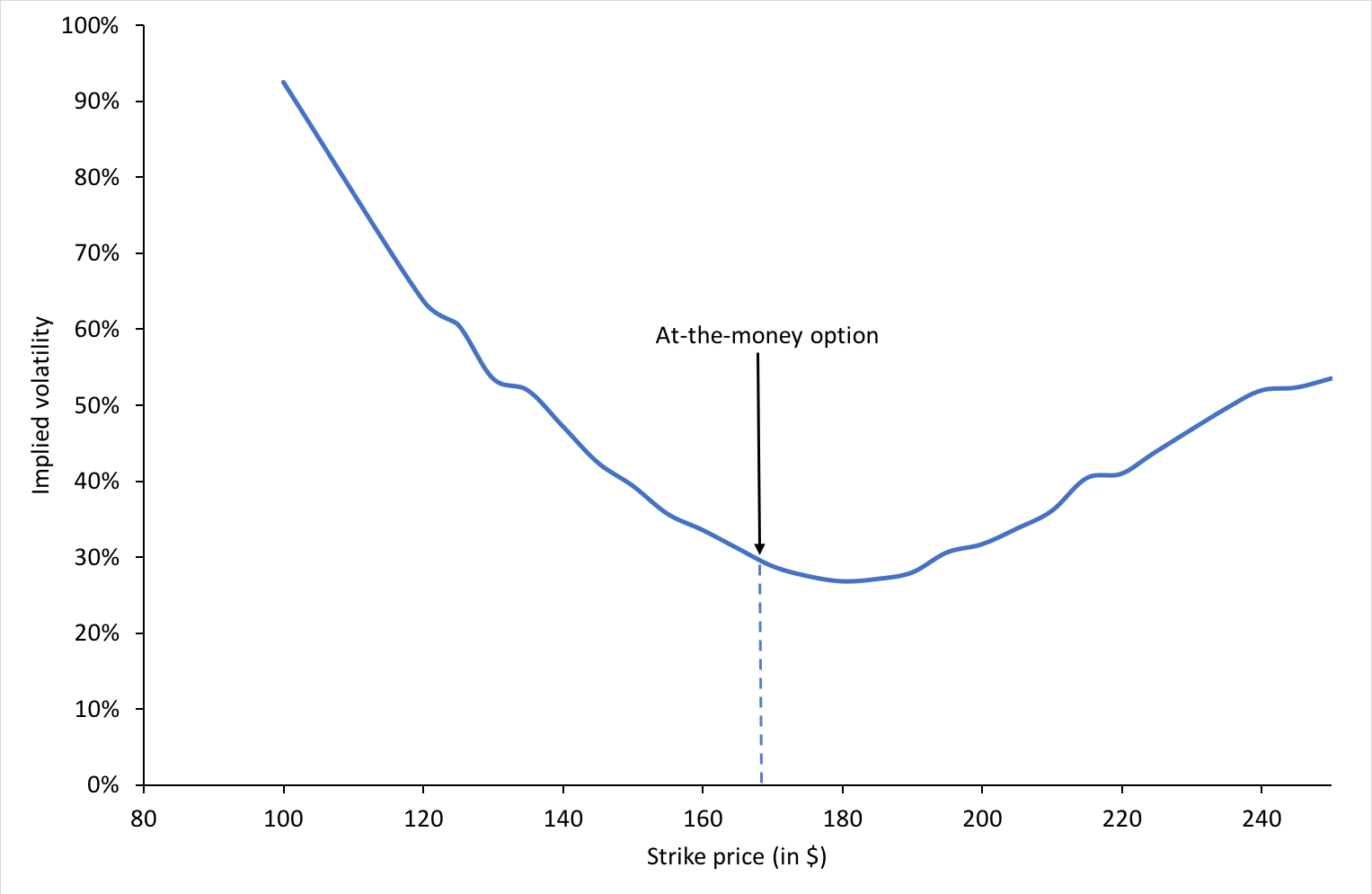


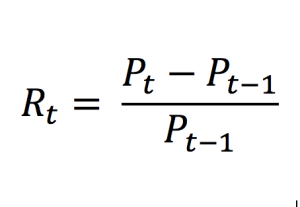
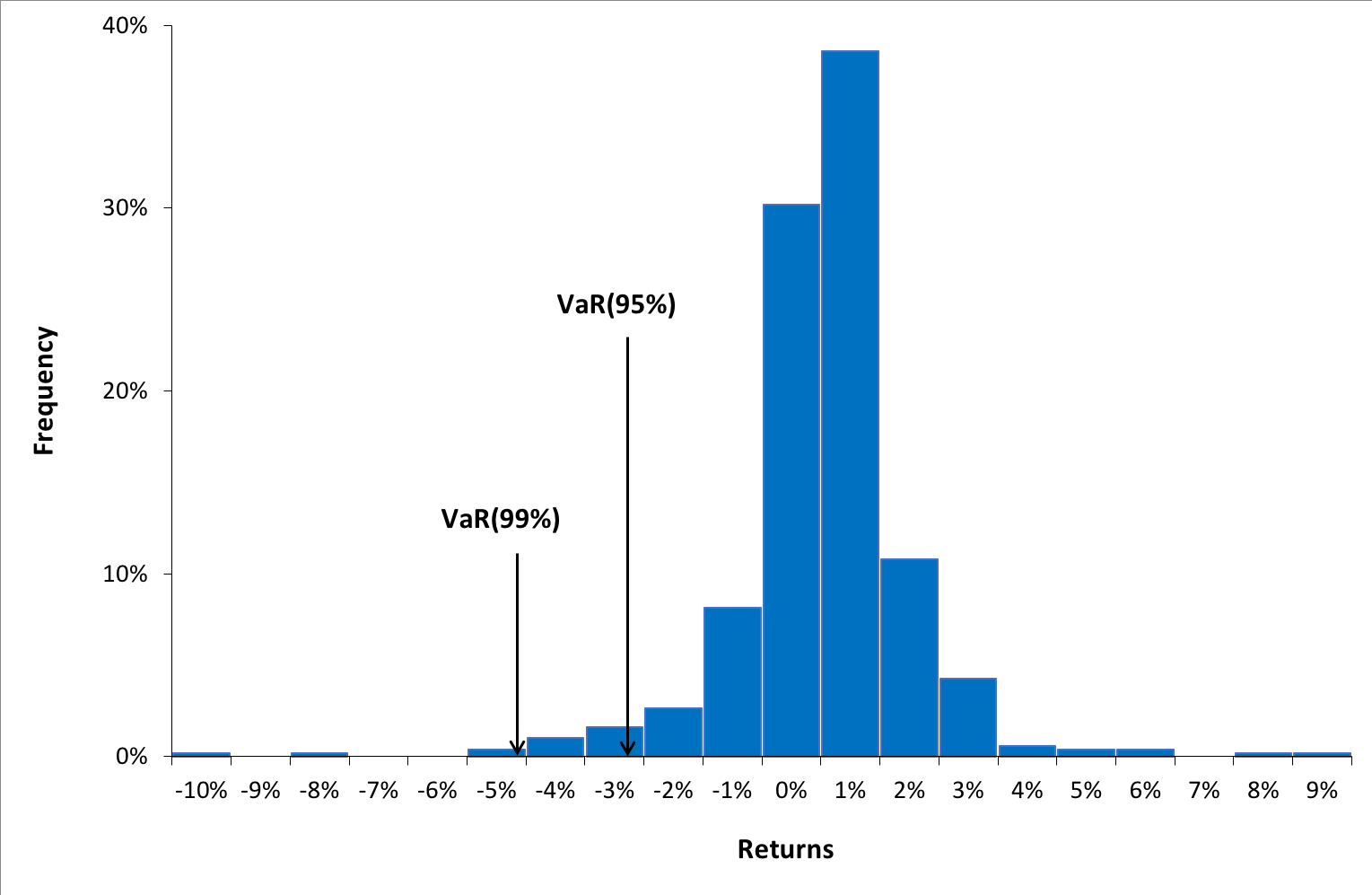
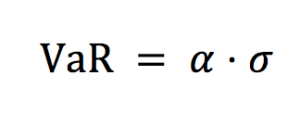
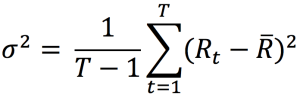
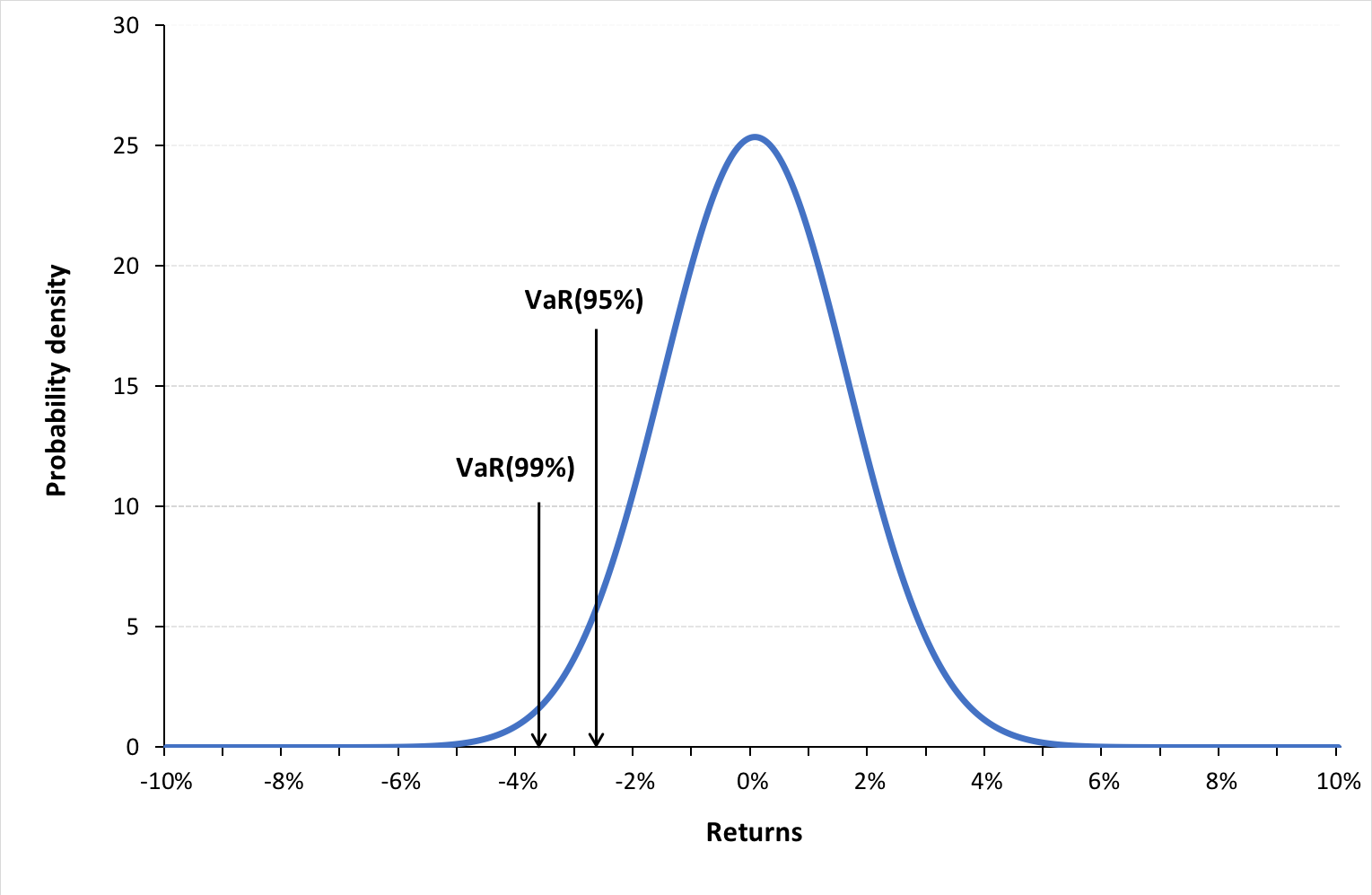
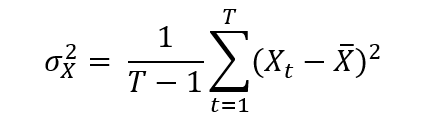
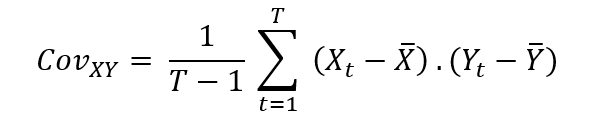
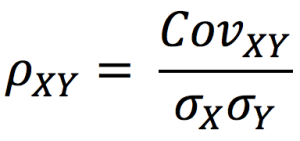
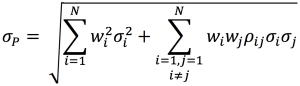
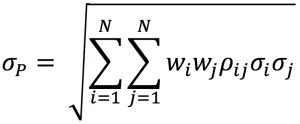
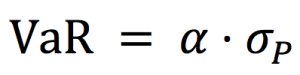
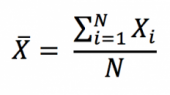
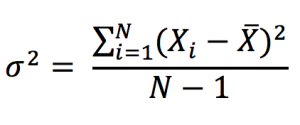
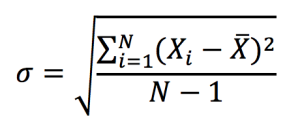
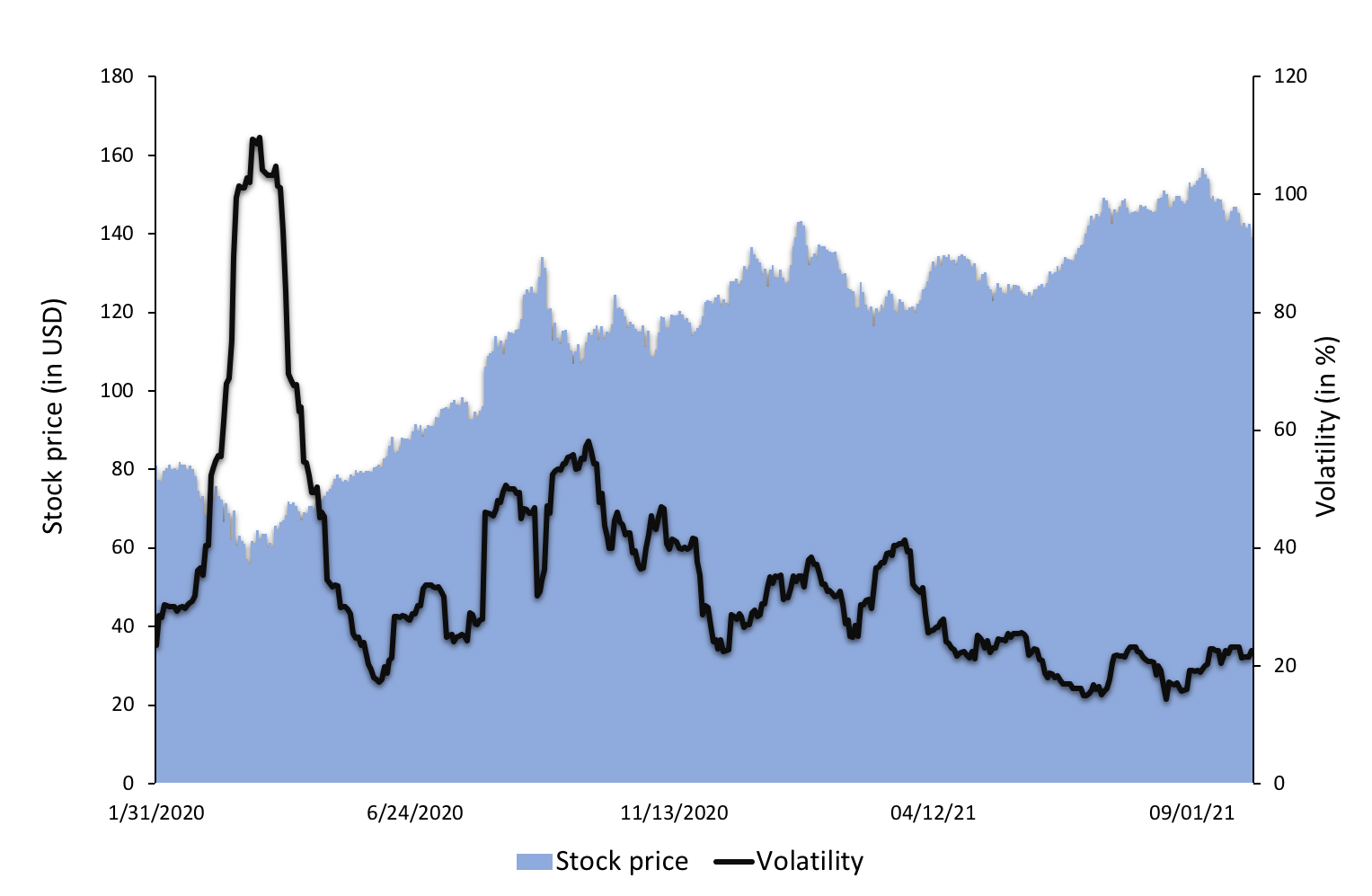

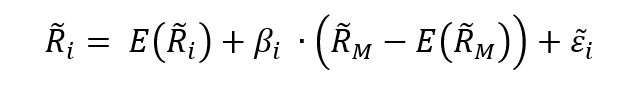
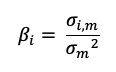
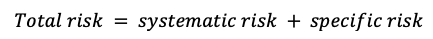
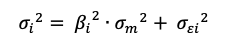
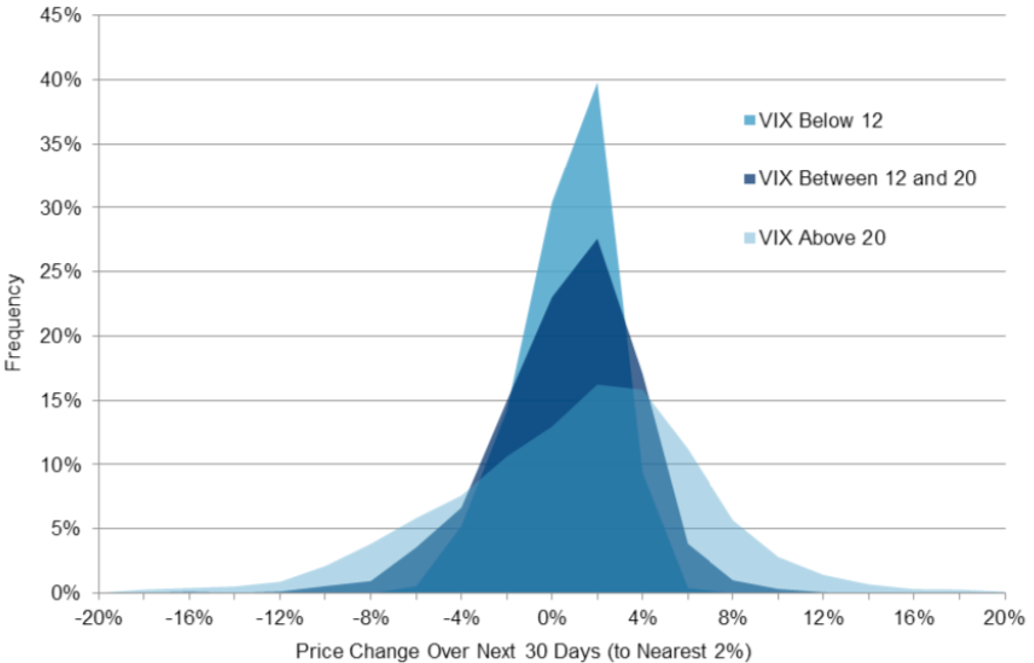
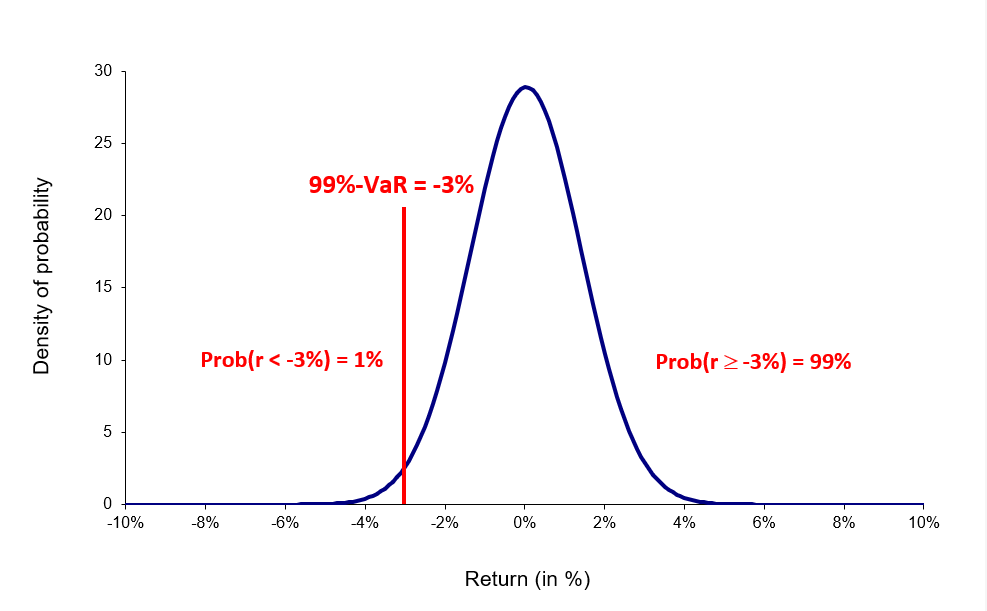
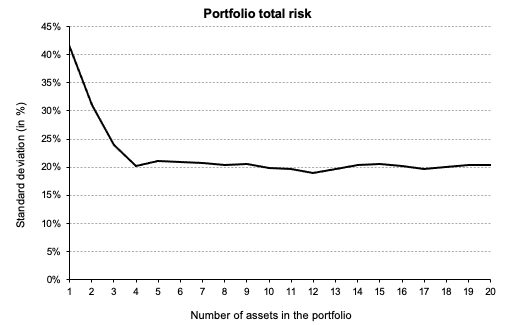 Source: Computations from the author.
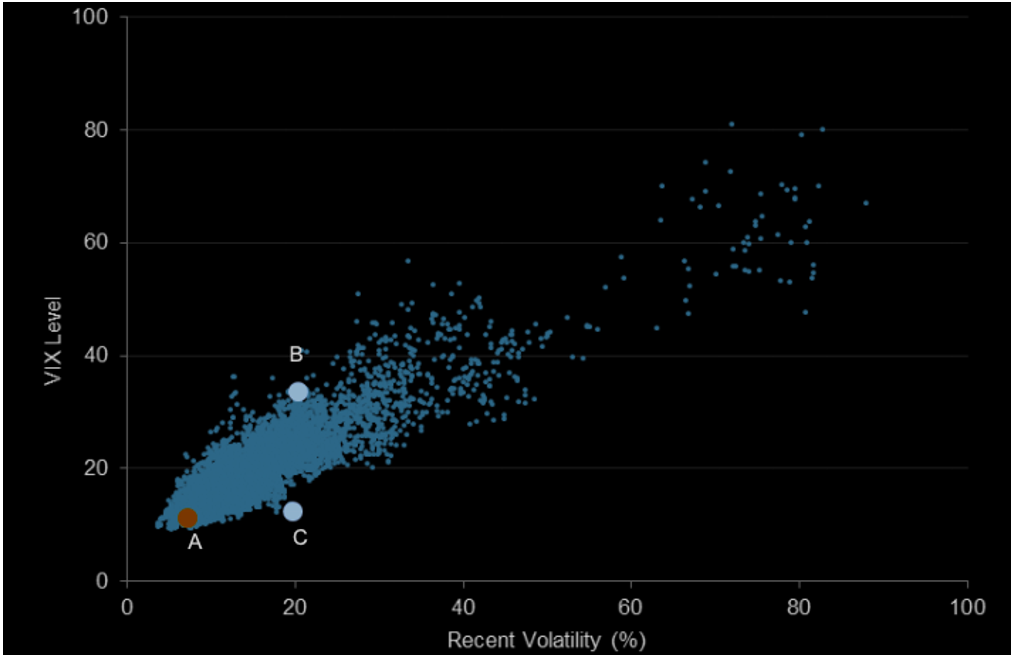
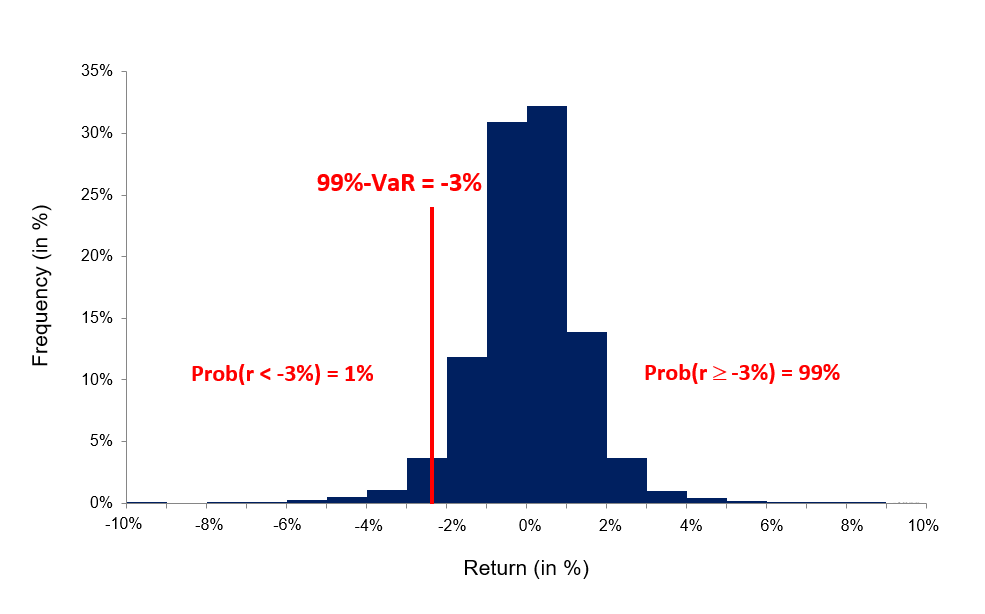
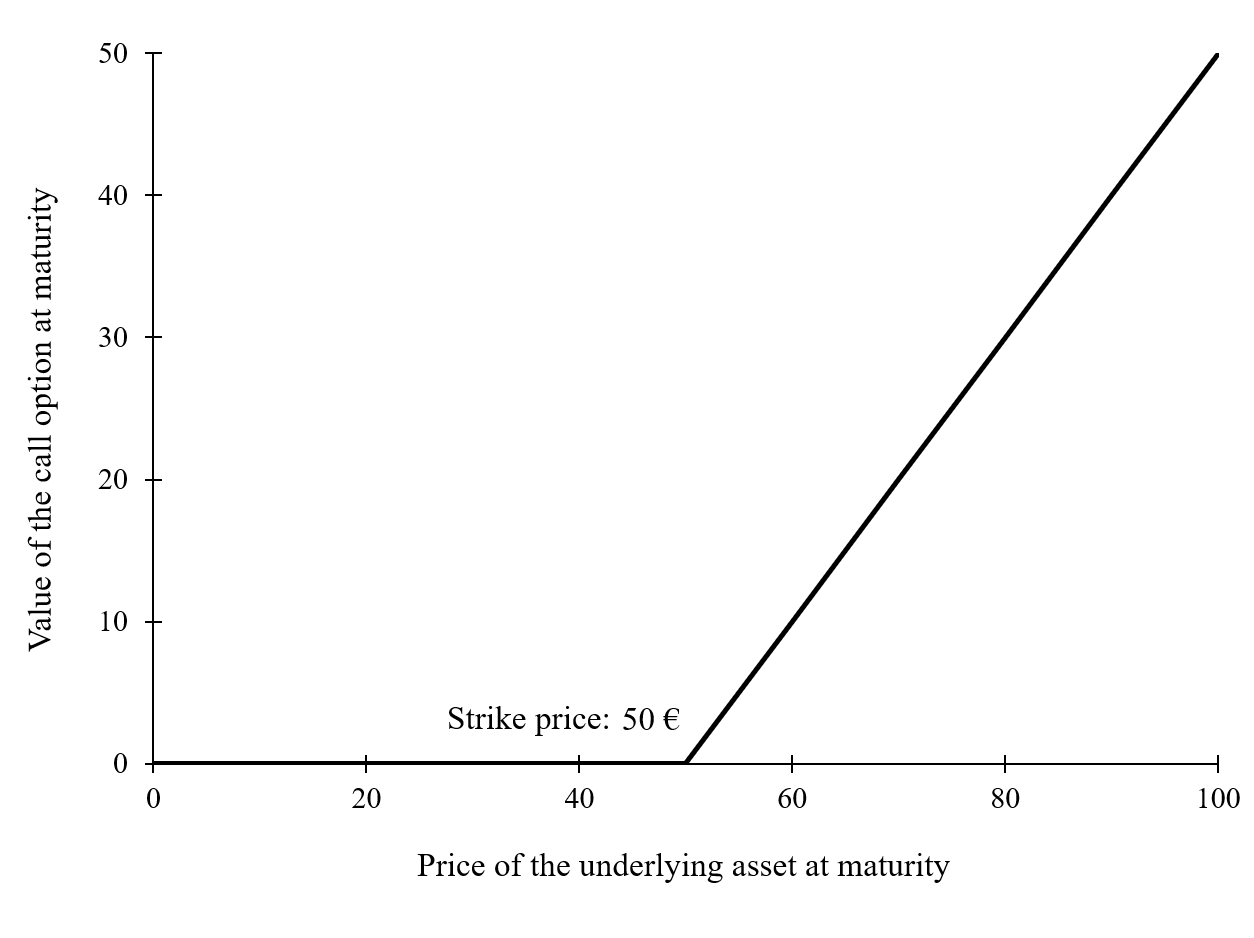
Source: Computations from the author.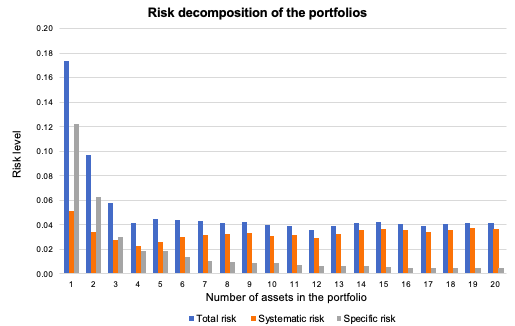 Source: Computations from the author.
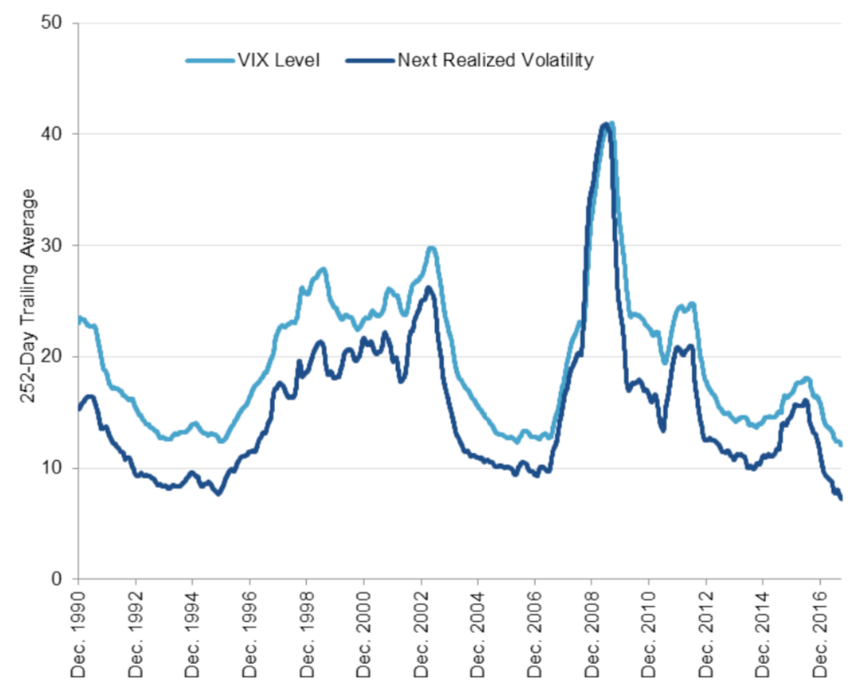
Source: Computations from the author.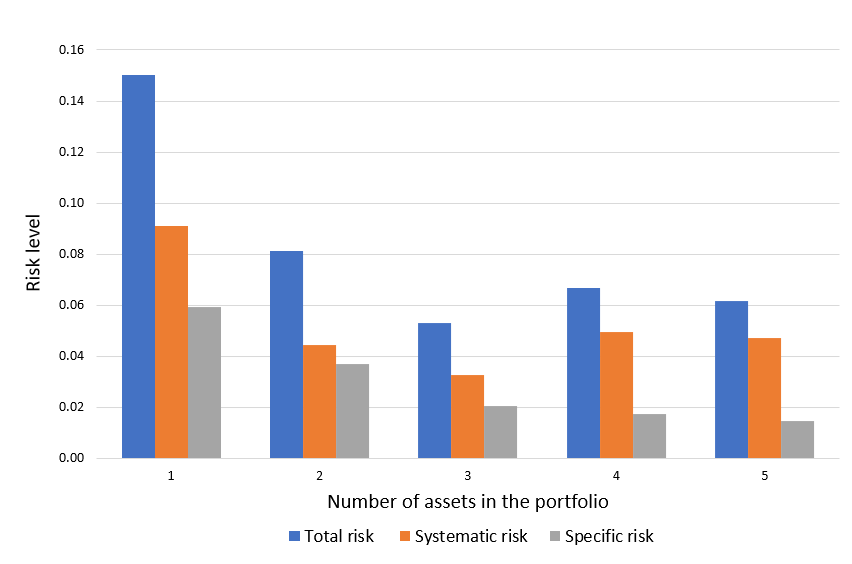 Source: Computation from the author.
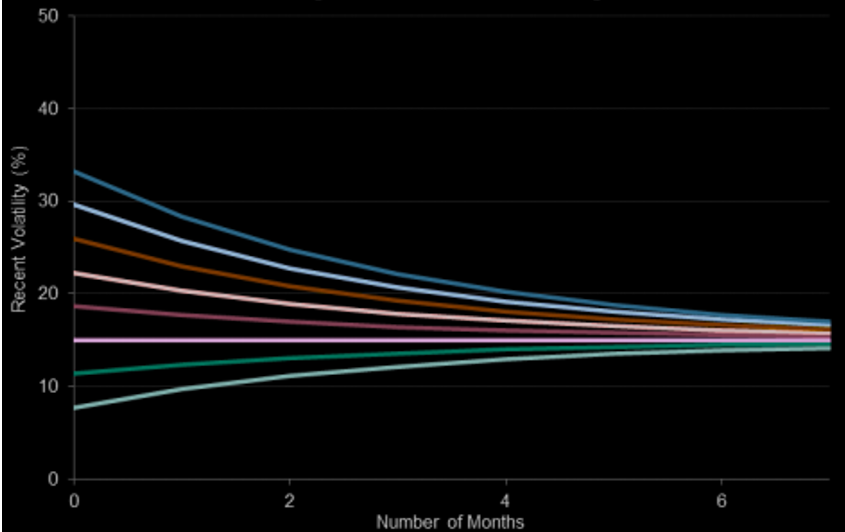
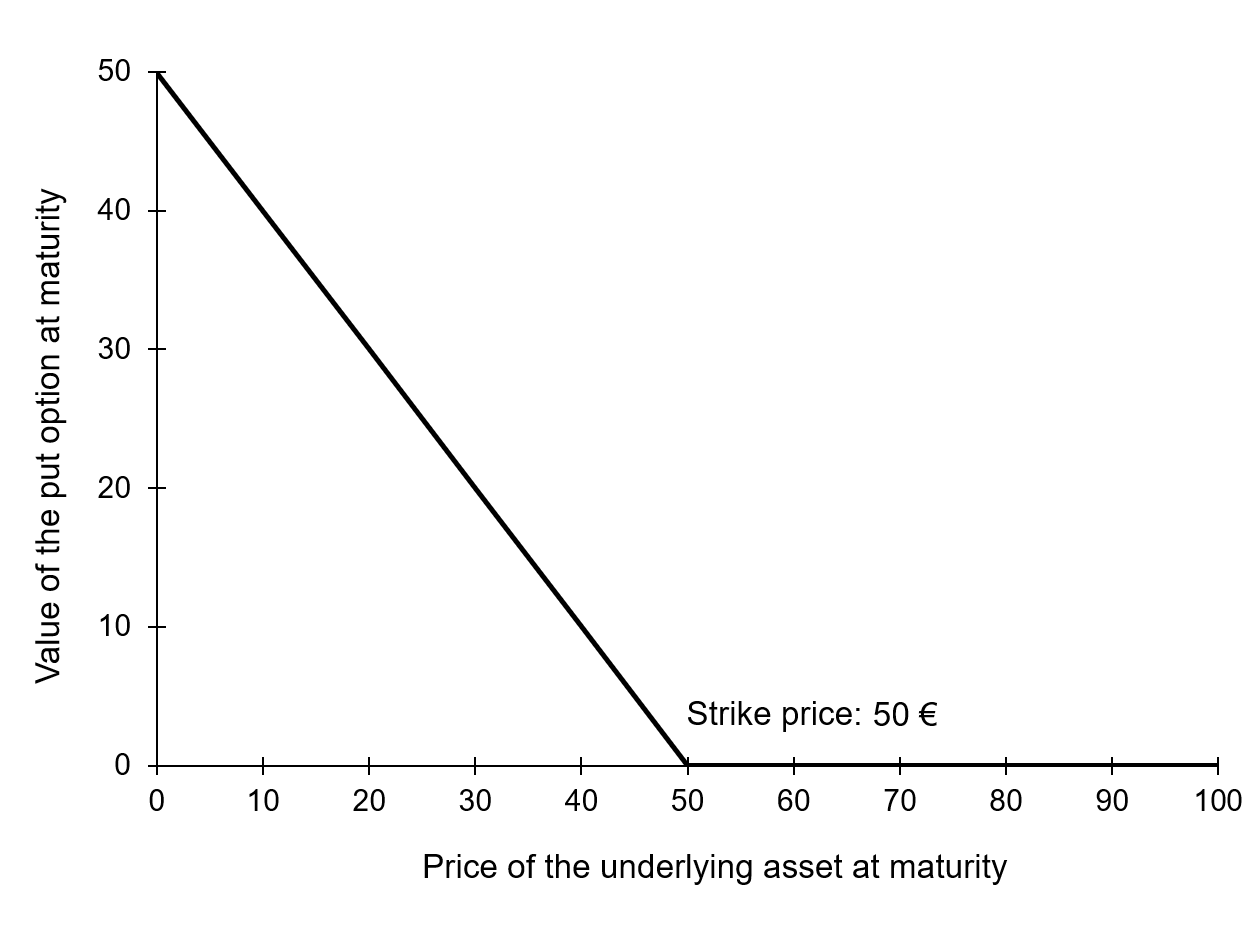
Source: Computation from the author.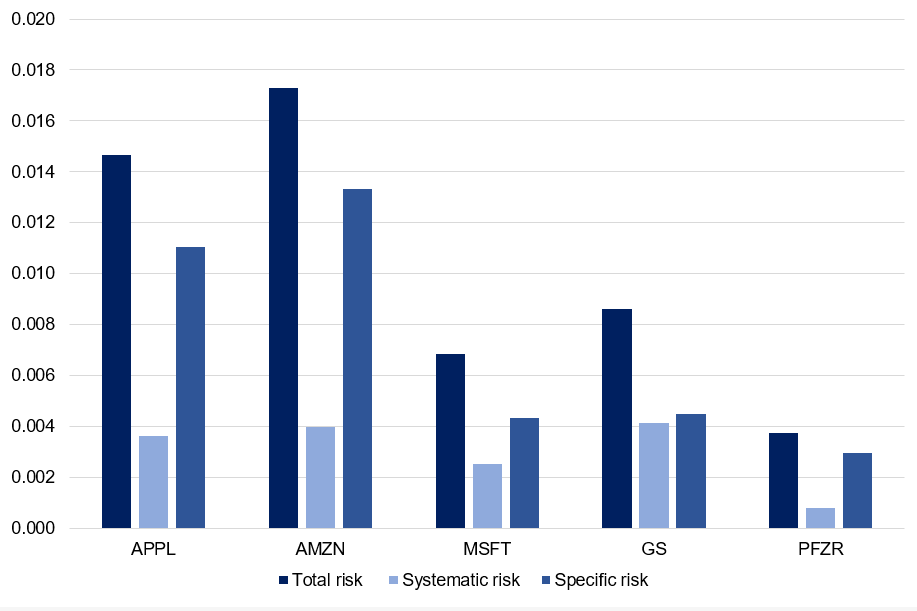 Source: Computation from the author.
Source: Computation from the author.