Pricing barrier options with simulations and sensitivity analysis with Greeks
In this article, Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2023) explains the pricing of barrier options with Monte-Carlo simulations and the sensitivity analysis of barrier options from the perspective of Greeks.
Pricing of discretely monitored barrier options with Monte-Carlo simulations
With the simulation method, only the pricing of discretely monitored barrier options can be handled since it is impossible to simulate continuous price trajectories with no intervals. Here the method is illustrated with a down-and-out put option. The general setup of economic details of the down-and-out put option and related market information are presented as follows:
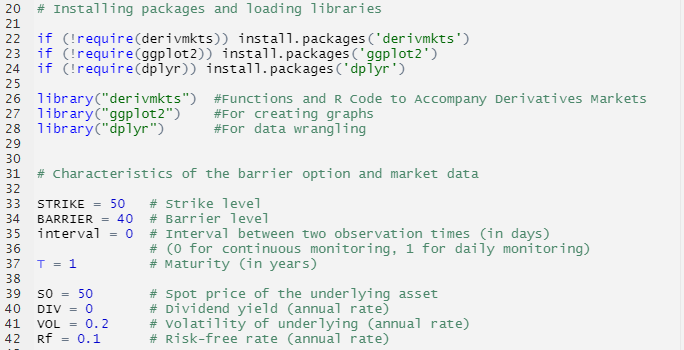
Similar to the simulation method for pricing standard vanilla options, Monte Carlo simulations based on Geometric Brownian Motion could also be employed to analyze the pricing of barrier options.
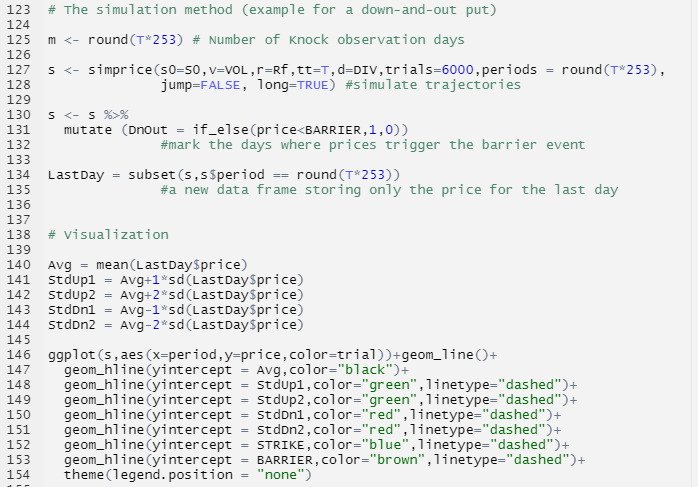
Figure 1. Trajectories of 600 price simulations.
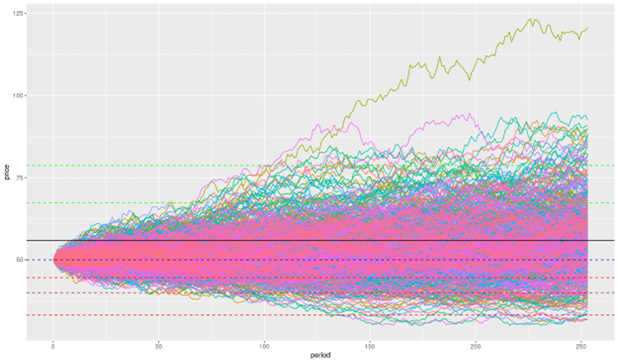
With the R script presented above, we can simulate 6,000 times with the simprice() function from the derivmkts package. Trajectories of 600 price simulations are presented above, with the black line representing the mean of the final prices, the green dashed lines 1x and 2x standard deviation above the mean, the red dashed lines 1x and 2x derivation below the mean, the blue dashed line the strike level and the brown line the knock-out level.
The simprice() function, according to the documentation, computes simulated lognormal price paths with the given parameters.
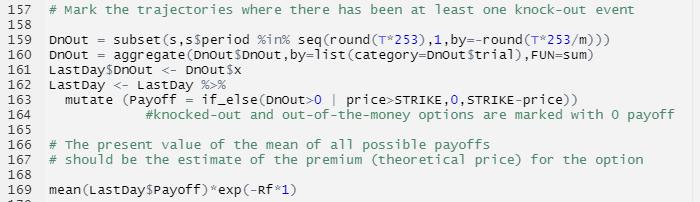
With this simulation of 6,000 price paths, we arrive at a price of 0.6720201, which is quite close to the one calculated from the formulaic approach from the previous post.
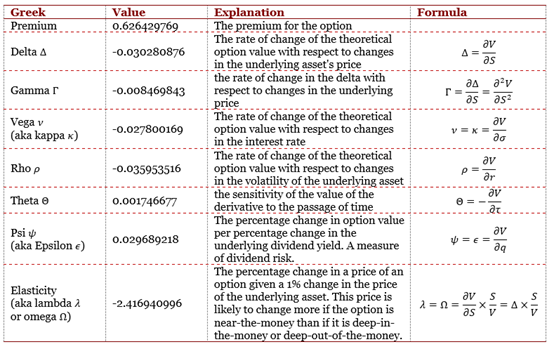
Analysis of Greeks
The Greeks are the measures representing the sensitivity of the price of derivative products including options to a change in parameters such as the price and the volatility of the underlying asset, the risk-free interest rate, the passage of time, etc. Greeks are important elements to look at for risk management and hedging purposes, especially for market makers (dealers) since they do not essentially take these risks for themselves.
In R, with the combination of the greeks() function and a barrier pricing function, putdownout() in this case, we can easily arrive at the Greeks for this option.

Table 1. Greeks of the Down-and-Out Put
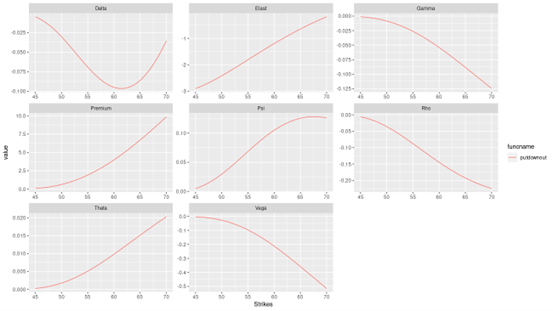
We can also have a look at the evolutions of the Greeks with the change of one of the parameters. The following R script presents an example of the evolutions of the Greeks along with the changes in the strike price of the down-and-out put option.

Figure 2. Evolution of Greeks with the change of Strike Price of a Down-and-Out Put
Download R file to price barrier options
You can find below an R file (file with txt format) to price barrier options.
Why should I be interested in this post?
As one of the most traded but the simplest exotic derivative products, barrier options open an avenue for different applications. They are also very often incorporated in structured products, such as reverse convertibles. It is, therefore, important to be equipped with knowledge of this product and to understand the pricing logics if one aspires to work in the domain of market finance.
Simulation methods are very common in pricing derivative products, especially for those without closed-formed pricing formulas. This post only presents a simple example of pricing barrier options and much optimization is needed for pricing more complex products with more rounds of simulations.
Related posts on the SimTrade blog
▶ Shengyu ZHENG Barrier options
▶ Shengyu ZHENG Pricing barrier options with analytical formulas
Useful resources
Academic articles
Broadie, M., Glasserman P., Kou S. (1997) A Continuity Correction for Discrete Barrier Option. Mathematical Finance, 7:325-349.
Merton, R. (1973) Theory of Rational Option Pricing. The Bell Journal of Economics and Management Science, 4:141-183.
Paixao, T. (2012) A Guide to Structured Products – Reverse Convertible on S&P500
Reiner, E.S., Rubinstein, M. (1991) Breaking down the barriers. Risk Magazine, 4(8), 28–35.
Rich, D. R. (1994) The Mathematical Foundations of Barrier Option-Pricing Theory. Advances in Futures and Options Research: A Research Annual, 7:267-311.
Wang, B., Wang, L. (2011) Pricing Barrier Options using Monte Carlo Methods, Working paper.
Books
Haug, E. (1997) The Complete Guide to Option Pricing. London/New York: McGraw-Hill.
Hull, J. (2006) Options, Futures, and Other Derivatives. Upper Saddle River, N.J: Pearson/Prentice Hall.
About the author
The article was written in June 2022 by Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2023).


