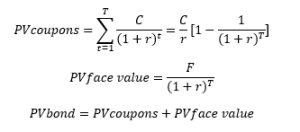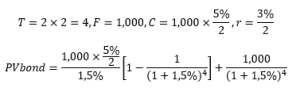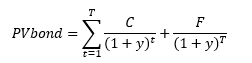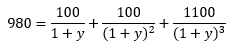Bond valuation
In this article, Rodolphe CHOLLAT-NAMY (ESSEC Business School, i>Grande Ecole – Master in Management, 2019-2023) introduces you to bond valuation.
Investors seek to determine how the different characteristics of a bond can influence its intrinsic value in order to know whether it is a good investment or not. To do this, they will look at the theoretical value of a bond, i.e. its present value. How can this be determined? How to interpret it?
Present value of a bond
The price of a bond is equal to the present value of the cash flows it generates. The holder of a bond will, by definition, receives a set of cash flows that will be received over a period of time. These flows are not directly comparable. A euro at time t1 does not have the same value as a euro at time t2. It is therefore necessary to determine the present value of future cash flows generated by the bond. This is calculated by multiplying these flows by a discount factor.
The discount rate chosen for this operation is determined by observing those already applied on the market to bonds comparable in duration, liquidity and credit risk. The convention is to discount all flows at a single rate, even if this does not reflect reality.
The present value of a bond is equal to the sum of the present value of the nominal amount and the present value of future coupons.
Where:
- C = coupon payment
- r = discount rate
- F = face value of the bond
- t = time of cash flow payment
- T = time to maturity
This formula shows that the present value of the security varies with the discount rate. In addition, the longer a bond has to mature, the greater the impact of discounted income on the value. This is known as the bond’s sensitivity.
Note that this formula includes the accrued coupon. This is known as the <i>gross</i> price. Most often the price in question is the price at the coupon footer. This is known as the clean price.
Now, let us see an application of this formula:
Consider a 2-year coupon bond with a 5% coupon rate and a nominal value of €1,000. We assume that coupons are paid semi-annually. A 3% discount rate is used. What is its present value?
The result is PVbond = €1,038.54
Yield To Maturity (YMT)
The YTM (“taux de rendement actuariel” in French) represents the rate of return on a bond for someone who buys it today and holds it to maturity. This is equivalent to the internal rate of return (IRR) of an investment in a bond if the investor holds the bond until maturity, with all payments made as scheduled and reinvested at the same rate.
To calculate the yield to maturity of a bond, the compound interest – in other words “interest on interest” – method is used. This method takes into account the fact that the interest from holding a bond is added back to the principal each year and itself generates interest.
The YTM is the rate that equates the price of the bond with the present value of the future coupons and the final repayment.
We therefore have the following relation:
Where y corresponds to the YTM.
Example
Let us take an example:
Consider a 3-year coupon bond with a 10% coupon rate and a nominal value of €1,000. We assume that the present value of the bond is €980. What is the yield to maturity?
To find out the yield to maturity, you have to solve the following equation:
The YMT is 10.82%.
If a bond’s coupon rate is less than its YMT, then the bond is selling at a discount. If a bond’s coupon rate is more than its YMT, then the bond is selling at a premium. If a bond’s rate is equal to its YTM, then the bond is selling at par.
Related posts on the SimTrade blog
▶ Rodolphe CHOLLAT-NAMY Introduction to bonds
▶ Rodolphe CHOLLAT-NAMY Government debt
▶ Rodolphe CHOLLAT-NAMY Corporate debt
▶ Rodolphe CHOLLAT-NAMY Bond markets
▶ Rodolphe CHOLLAT-NAMY Bond risks
Useful resources
longin.fr Evaluation d’obligations à taux fixe
About the author
Article written in May 2021 by Rodolphe CHOLLAT-NAMY (ESSEC Business School, i>Grande Ecole – Master in Management, 2019-2023).