Moments d’une distribution statistique

Dans cet article, Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2023) présente les quatre premiers moments d’une distribution statistique : la moyenne, la variance, la skewness et la kurtosis.

Variable aléatoire

Une variable aléatoire est une variable dont la valeur est déterminée d’après la réalisation d’un événement aléatoire. Plus précisément, la variable (X) est une fonction mesurable depuis un ensemble de résultats (Ω) à un espace mesurable (E).

X : Ω → E

X est une variable aléatoire réelle à condition que l’espace mesurable (E) soit, ou fasse partie de, l’ensemble des nombres réels (ℝ).

Je présente un exemple avec la rentabilité d’un investissement dans l’action Apple. La figure 1 ci-dessous représente la série temporelle de la rentabilité journalière de l’action Apple sur la période allant de novembre 2017 à novembre 2022.

Figure 1. Série temporelle de rentabilités de l’action Apple.

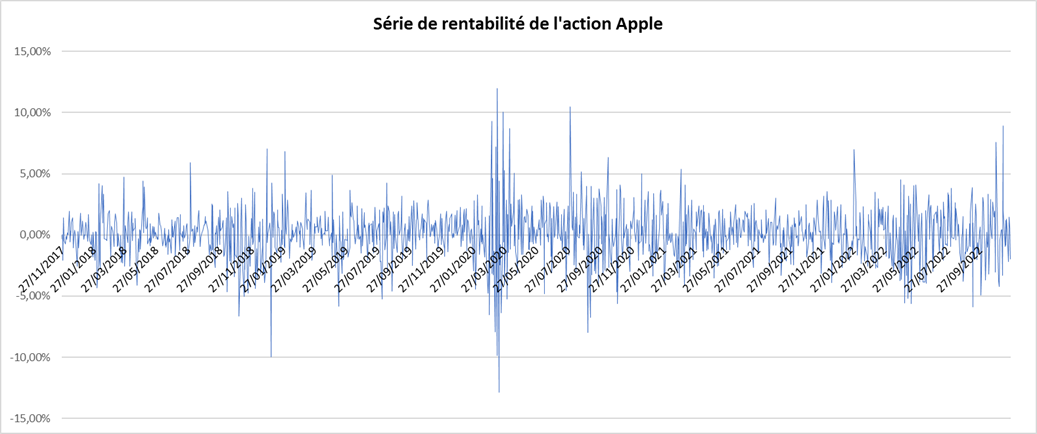
Source : calcul par l’auteur (données : Yahoo Finance).

Figure 2. Histogramme des rentabilités de l’action Apple.

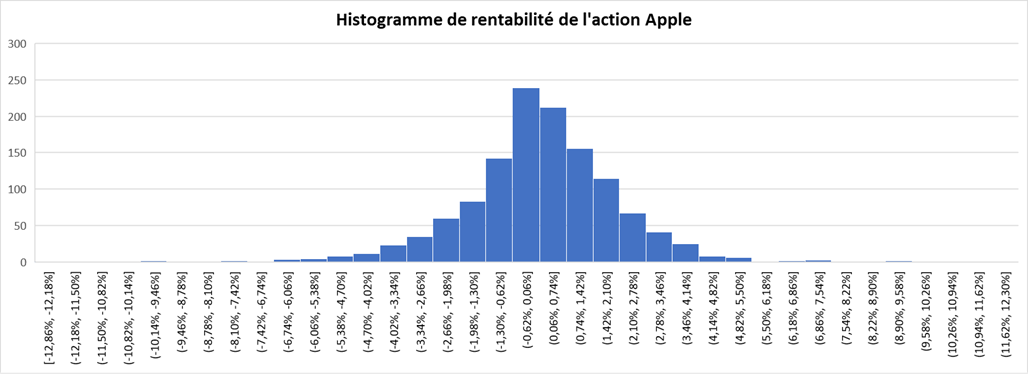
Source : calcul par l’auteur (données : Yahoo Finance).

Moments d’une distribution statistique

Le moment d’ordre r ∈ ℕ est un indicateur de la dispersion de la variable aléatoire X. Le moment ordinaire d’ordre r est défini, s’il existe, par la formule suivante :

m_r = 𝔼 (X^r)

Nous avons aussi le moment centré d’ordre r défini, s’il existe, par la formule suivante :

c_r = 𝔼([X-𝔼(X)]^r)

Moment d’ordre un : la moyenne

Définition

La moyenne ou l’espérance mathématique d’une variable aléatoire est la valeur attendue en moyenne si la même expérience aléatoire est répétée un grand nombre de fois. Elle correspond à une moyenne pondérée par probabilité des valeurs que peut prendre cette variable, et elle est donc connue comme la moyenne théorique ou la vraie moyenne.

Si une variable X prend une infinité de valeurs x₁, x₂,… avec les probabilités p₁, p₂,…, l’espérance de X est définie comme :

Μ = m₁= 𝔼(X) = ∑^∞_i=1p_ix_i

L’espérance existe à condition que cette somme soit absolument convergente.

Estimation statistique

La moyenne empirique est un estimateur de l’espérance. Cet estimateur est sans biais, convergent (selon la loi des grands nombres), et distribué normalement (selon le théorème centrale limite).

A partir d’un échantillon de variables aléatoire réelles indépendantes et identiquement distribuées (X₁,…,X_n), la moyenne empirique est donc :

X̄ = (∑ⁿ_i=1x_i)/n

Pour une loi normale centrée réduite (μ = 0 et σ = 1), la moyenne est égale à zéro.

Moment d’ordre deux : la variance

Définition

La variance (moment d’ordre deux) est une mesure de la dispersion des valeurs par rapport à sa moyenne.

Var(X) = σ ² = 𝔼[(X-μ)²]

Elle exprime l’espérance du carré de l’écart à la moyenne théorique. Elle est donc toujours positive.

Pour une loi normale centrée réduite (μ = 0 et σ = 1), la variance est égale à un.

Estimation statistique

A partir d’un échantillon (X₁,…,X_n), nous pouvons estimer la variance théorique à l’aide de la variance empirique :

S² = (∑ⁿ_i=1(x_i – X̄)²)/n

Cependant, cet estimateur est biaisé, parce que 𝔼(S²) = (n-1)/(n) σ². Nous avons donc un estimateur non-biaisé Š² = (∑ⁿ_i=1(x_i – X̄)²)/(n-1)

Application en finance

La variance correspond à la volatilité d’un actif financier. Une variance élevée indique une dispersion plus importante, et ce n’est pas favorable du regard des investisseurs rationnels qui présentent de l’aversion au risque. Ce concept est un paramètre clef dans la théorie moderne du portefeuille de Markowitz.

Moment d’ordre trois : la skewness

Définition

La skewness (coefficient d’asymétrie en bon français) est le moment d’ordre trois, défini comme ci-dessous :

γ₁ = 𝔼[((X-μ)/σ)³]

La skewness mesure l’asymétrie de la distribution d’une variable aléatoire. On distingue trois types de distributions selon que la distribution est asymétrique à gauche, symétrique, ou asymétrique à droite. Un coefficient d’asymétrie négatif indique une asymétrie à gauche de la distribution, dont la queue gauche est plus importante que la queue droite. Un coefficient d’asymétrie nul indique une symétrie, les deux queues de la distribution étant aussi importante l’une que l’autre. Enfin, un coefficient d’asymétrie positif indique une asymétrie à droite de la distribution, dont la queue droite est plus importante que la queue gauche.

Pour une loi normale, la skewness est égale à zéro car cette loi est symétrique par rapport à la moyenne.

Moment d’ordre quatre : la kurtosis

Définition

La kurtosis (coefficient d’acuité en bon français) est le moment d’ordre quatre, défini par :

β₂ = 𝔼[((X-μ)/σ)⁴]

Il décrit l’acuité d’une distribution. Un coefficient d’acuité élevé indique que la distribution est plutôt pointue en sa moyenne, et a des queues de distribution plus épaisses (fatter tails en anglais).

Le coefficient d’une loi normale est de 3, autrement dit, une distribution mésokurtique. Au-delà de ce seuil, une distribution est appelée leptokurtique. Les distributions présentes au marché financier sont principalement leptokurtique, impliquant que les valeurs anormales et extrêmes sont plus fréquentes que celles d’une distribution gaussienne. Au contraire, un coefficient d’acuité de moins de 3 indique une distribution platykurtique, dont les queues sont plus légères.

Pour une loi normale, la kurtosis est égale à trois.

Exemple : distribution des rentabilités d’un investissement dans l’action Apple

Nous donnons maintenant un exemple en finance en étudiant la distribution des rentabilités de l’action Apple. Dans les données récupérées de Yahoo! Finance pour la période allant de novembre 2017 à novembre 2022, on se sert de la colonne du cours de clôture pour calculer les rentabilités journalières. Nous utilisons des fonctions Excel afin de calculer les quatre premiers moments de la distribution empirique des rentabilités de l’action Apple comme indiqué dans la table ci-dessous.

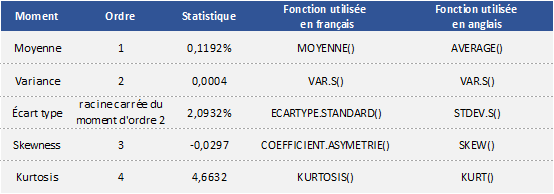
Pour une distribution normale standard (centrée réduite), la moyenne est de zero, la variance est de 1, le skewness est de zéro, et le kurtosis est de 3. À comparaison avec une distribution normale, la distribution de rentabilité de l’action Apple a une moyenne légèrement positive. Cela signifie qu’à long terme, la rentabilité de l’investissement dans cet actif est positive. Son skewness est négatif, indiquant l’asymétrie vers la gauche (les valeurs négatives). Son kurtosis est supérieur de 3, ce qui indique que les extrémités sont plus épaisses que la distribution normale.

Fichier Excel pour calculer les moments

Vous pouvez télécharger le ficher Excel d’analyse des moments de l’action Apple en suivant le lien ci-dessous :

Autres article sur le blog SimTrade

▶ Shengyu ZHENG Catégories de mesures de risques

▶ Shengyu ZHENG Mesures de risques

Ressources

Articles académiques

Robert C. Merton (1980) On estimating the expected return on the market: An exploratory investigation, Journal of Financial Economics, 8:4, 323-361.

Données

Yahoo! Finance Données de marché pour l’action Apple

A propos de l’auteur

Cet article a été écrit en janvier 2023 par Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2023).