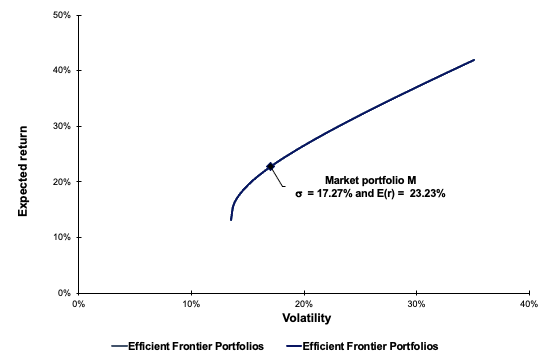
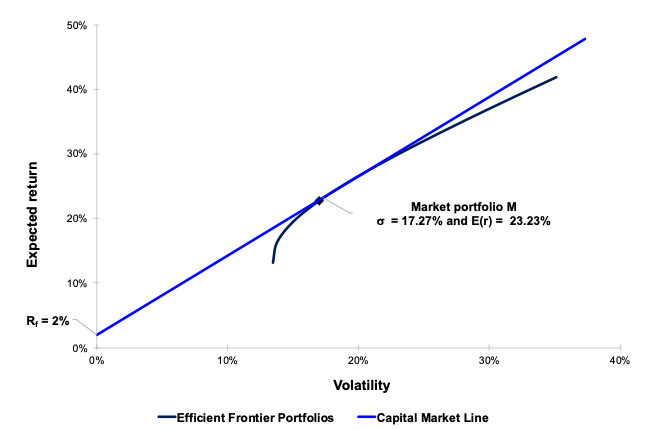
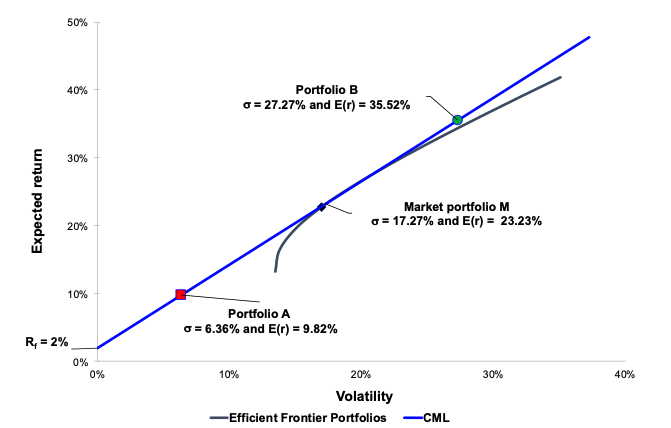
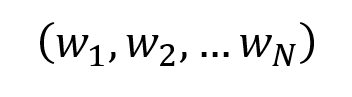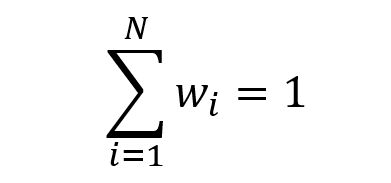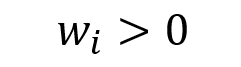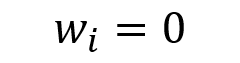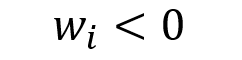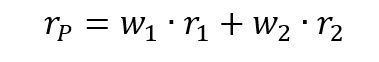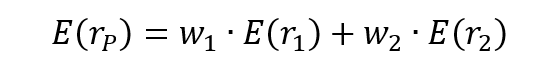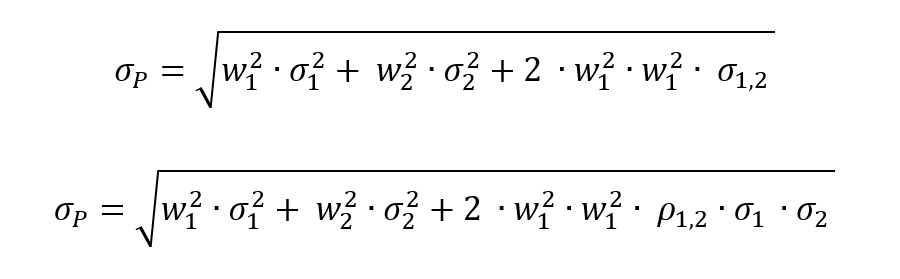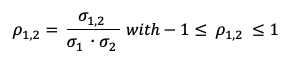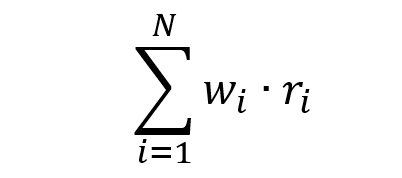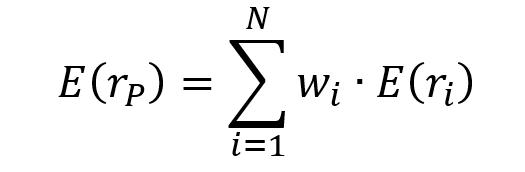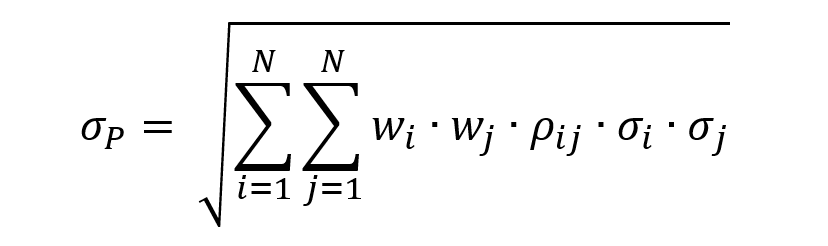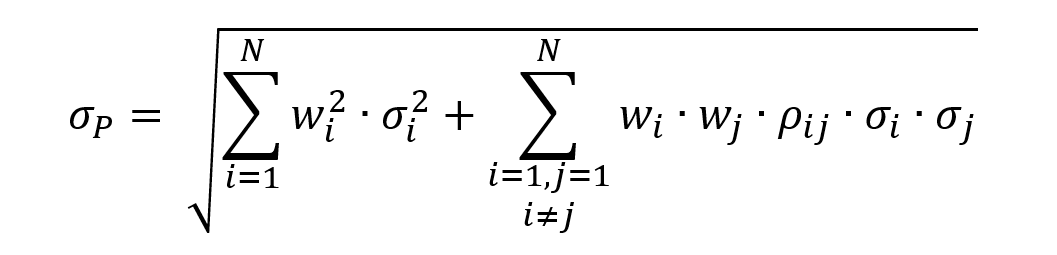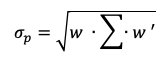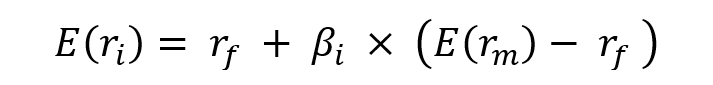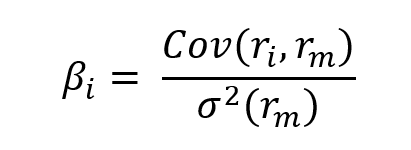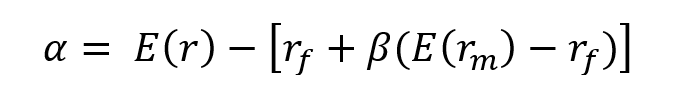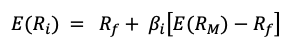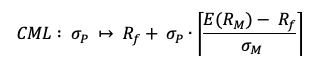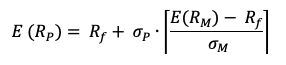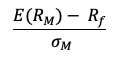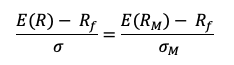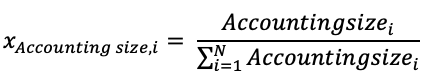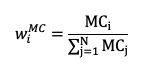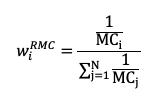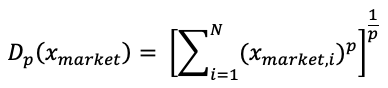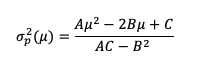In this article, Youssef LOURAOUI (Bayes Business School, MSc. Energy, Trade & Finance, 2021-2022) elaborates on the concept of Hedge Funds. Hedge funds are a type of asset class that differs from standard fixed-income and equities investments in terms of risk/return profile.
The structure of this article is as follows: First, we will define a hedge fund. Second, we provide a historical perspective on the first known hedge fund. Third, we will discuss hedge fund fees. Fourth, we discuss the conventional long-short strategy and provide an overview of the major hedge fund strategies. And finally, we end by discussing the economic importance of hedge funds.
Introduction
There is no straightforward definition of a hedge fund. Simply said, a hedge fund is an investment vehicle that aims to create performance by employing a variety of complex trading strategies. When the first hedge fund was introduced, the term “hedge” referred to lowering risk by investing in both long and short positions at the same time.
Hedge funds are exempted from the financial regulations that apply to other investment vehicles such as mutual funds. On the one hand, hedge funds have a lot of freedom to implement their investment strategy and face minimal disclosure rules. Hedge funds have the freedom to utilize leverage using derivatives products. On the other hand, hedge funds are restricted in the way they raise money from investors. Hedge fund investors must be “accredited investors,” which means they must have a particular amount of financial wealth and/or financial education to invest. Hedge funds have also been subject to a non-solicitation restriction, which means they are not allowed to advertise or aggressively seek individuals for investment.
According to the Security Exchange Commission (SEC, ), the governmental branch for regulated financial markets in the US, a hedge fund can be defined as follows:
“Hedge fund’ is a general, non-legal term used to describe private, unregistered investment pools that traditionally have been limited to sophisticated, wealthy investors. Hedge funds are not mutual funds and, as such, are not subject to the numerous regulations that apply to mutual funds for the protection of investors – including regulations requiring a certain degree of liquidity, regulations requiring that mutual fund shares be redeemable at any time, regulations protecting against conflicts of interest, regulations to assure fairness in the pricing of fund shares, disclosure regulations, regulations limiting the use of leverage, and more.” (SEC)
The first hedge fund: Jones
In 1949, Alfred Winslow Jones is said to have founded the first professional hedge fund and is regarded as the “father of the hedge fund industry”. He set up the fund as a limited partnership, with the hedge fund manager providing significant initial capital and a few significant investors. The fund’s principal strategy was to use a long/short method, the fund being long on undervalued securities and short on overvalued securities. Jones based his investment approach on stock picking (he believed he lacked market timing skills). Hedge funds’ main idea is that they can use leverage to boost returns in both directions.
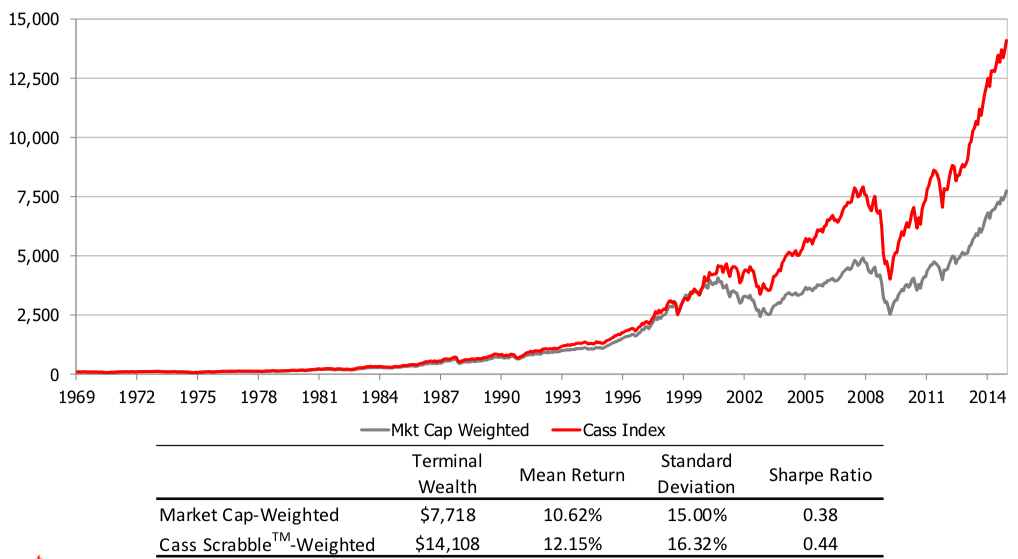
From 1955 to 1965, Jones is reported to have achieved a 670% return on his hedge fund by taking both long and short positions. Before Jones, short selling had been popular for a long time, but he realized that by balancing long and short positions, he could be relatively immune to overall market changes while benefiting from the relative outperformance of his long positions against his short positions. The performance of Jones’s fund is shown in Figure 1 about the Dow Jones Industrials index used as a benchmark and Fidelity’s highest performing mutual fund. Over the 1960-65 period, the fund managed to multiply its return by a factor of four, which is higher than the best performing mutual fund (Fidelity Trend Fund) and the Dow-Jones industrials.
Figure 1. Alfred Winslow Jones’s hedge fund performance between 1960-65.
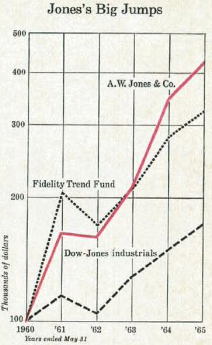
Source: “The Jones Nobody Keeps Up With” (Fortune, 1966).
Development of hedge funds
Interest in hedge funds grew after Fortune magazine published Jones’s results in 1966, and the Securities and Exchange Commission (SEC) listed 140 hedge funds in 1968. As institutional investors began to embrace hedge funds in the 1990s, the hedge fund industry saw a huge spike in interest. Hedge funds with billions of dollars under management were typical in the 2000s, with total hedge fund assets reaching a peak of nearly $2 trillion before the global financial crisis of 2008, dropping during the crisis, and recently reached a new peak.
Hedge funds’ aggregate positions are much larger than their assets under management due to their leverage, and their trading volume is a much larger part of the aggregate trading volume than their relative position sizes due to their high turnover, so hedge fund trading now accounts for a significant portion of all trading. Given a limited demand for liquidity, there is a limited amount of profit to be made and a limited requirement for active investment in an optimally inefficient market, the quantity of capital committed to hedge funds cannot keep expanding.
Hedge funds fees
Among the most frequent fees in the hedge fund industry, we can name the following:
Management fee
Management fee represents the fees that the hedge funds collect to run their operations (salaries, infrastructure, etc.). The management fee is usually about 3%
Performance fee
The performance fee is a compensation when the hedge fund achieves a certain level of performance. This threshold, called the hurdle rate, represents the minimum performance that a hedge fund has to achieve to charge an incentive fee. This motivates the hedge fund manager to perform and to align its interest with its clients’ interests. Beyond the hurdle rate, the outperformance is shared between the hedge fund manager (20%) and the clients (80%).
The high water mark (HWM) provision is a mechanism where the hedge fund will only charge performance fees if it manages to deliver returns above the returns of the previous period. If the hedge fund is down 50%, the performance achieved to recover the losses (100% won’t be subject to performance fees). Only after recovering entirely from the drawdown, the hedge fund can be entitled to earn the performance fee.
A classic hedge fund strategy: the long-short strategy
The long-short strategy is the strategy implemented by the first hedge fund (Alfred Winslow Jones fund). According to Credit Suisse, long-short equity funds engage in both the long and short sides of the equity markets, to diversify or hedge across sectors, regions, and market capitalizations. Managers can switch from value to growth, from small to medium to large capitalization equities, and from net long to net short positions. Managers can also trade stock futures and options, as well as equity-related instruments and debt, and form more concentrated portfolios than classic long-only equity funds.
To illustrate a long-short strategy, we create a hedge fund portfolio based on two stocks from the US equity market. We pick one overvalued stock and one undervalued stock based on their price-to-earnings (P/E) ratio. We chose for this purpose Twitter (overvalued) and Pfizer (undervalued). We download a time series of three-month worth of data for two stocks (Twitter and Pfizer) and the S&P500 index.
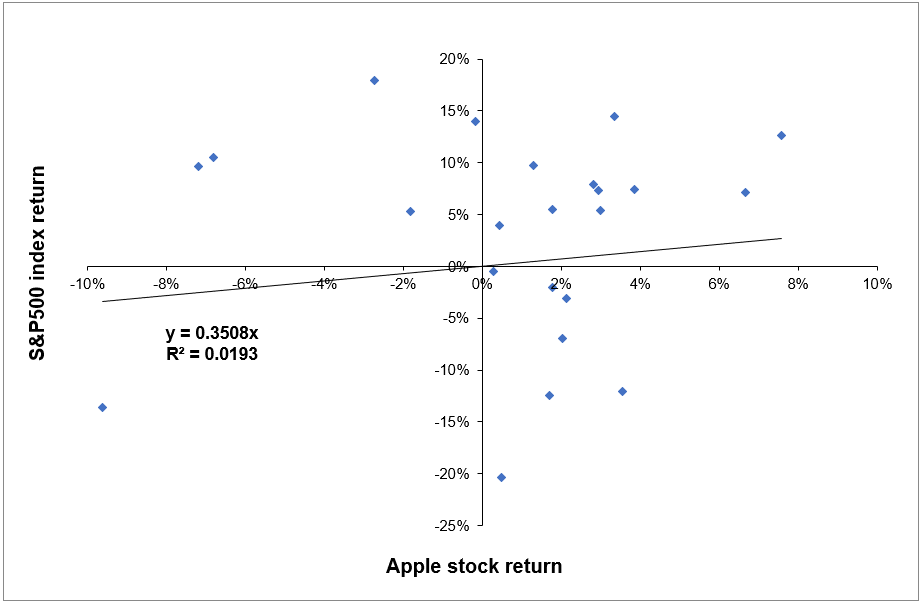
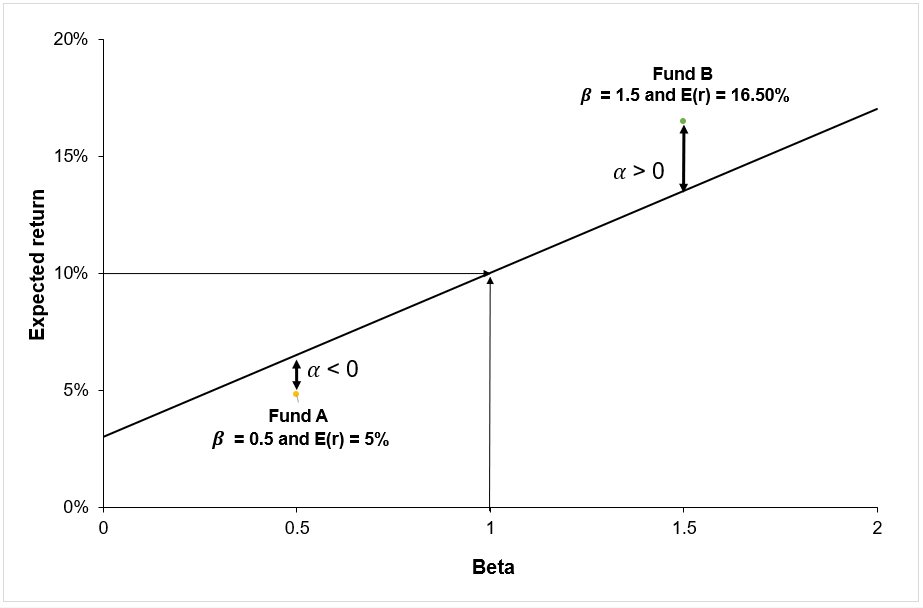
Figure 2 represents the regression of the returns of the simulated hedge fund portfolio on the S&P500 index. We can appreciate a null slope (0.0936) of the regression indicating the low correlation of the hedge fund with the market represented by the S&P500 index. This strategy is market-neutral, meaning that the portfolio is not correlated directly with the market fluctuations. The performance of a zero-beta portfolio would be derived from the alpha, a key metric in the portfolio management industry.
Figure 2. Regression of the hedge fund return on the S&P500 market index.
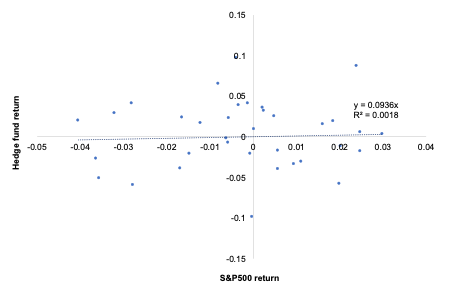
Source: computation by the author (data: Bloomberg).
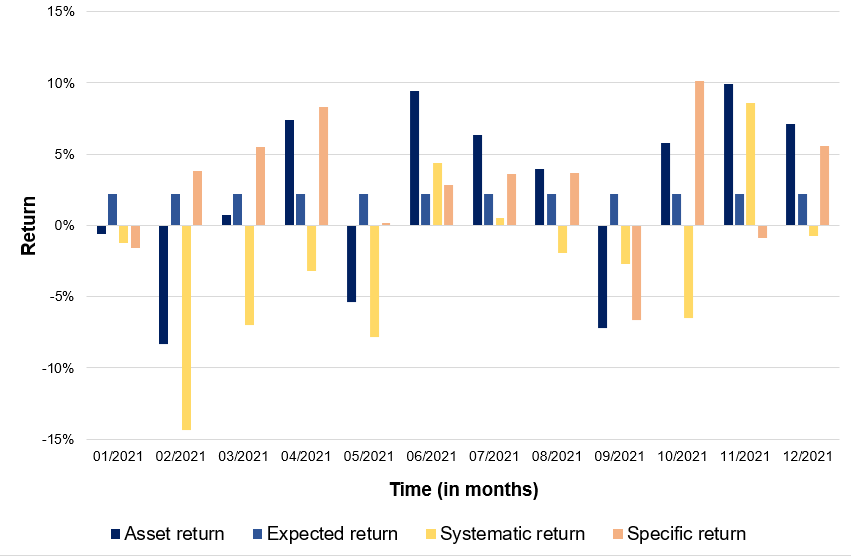
We compute the return and volatility of each security and the market index as a starting point. We also determine the correlation of the stocks to the market index. For the short position (Twitter), the sign of the correlation inverts of the sign. We compute an equally-weighted portfolio composed of two stocks: a long position on Pfizer and a short position on Twitter. This portfolio delivered a return of 0.27%, which is better than the broader stock index return over the same period (-0.22%).
Figure 3 depicts the return of the hedge fund portfolio relative to the market index return. From the analysis, the long-short strategy managed to outperform the S&P500 market index by 49 basis points. Even if the market is in a bearish setting, the strategy managed to deliver positive returns as the short position helps to be uncorrelated the return of the hedge fund from the market return.
Figure 3. Return of the hedge fund relative to the S&P500 market index.
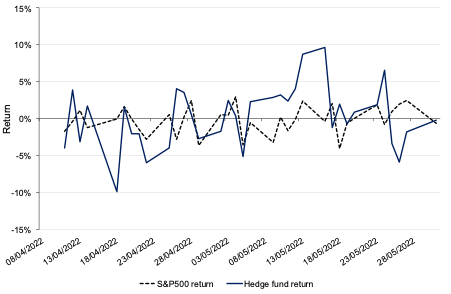
Source: computation by the author (data: Bloomberg).
You can download below the Excel file below which gives the details of the computation of the long-short strategy example.
Hedge fund role in economy
Hedge funds, for example, are frequently criticized in the media. Companies, for example, dislike seeing their shares shorted because it indicates a belief that the company’s share price will fall. Short sellers, including hedge funds, are sometimes blamed for a company’s problems, even though the stock price is usually falling due to the company’s poor financial condition, not because of any other source.
Hedge funds, in general, serve several important functions in the economy. First, they improve market efficiency by gathering information about businesses and incorporating it into prices through their trades. Because the capital market is the tool used to allocate resources in the economy, increased efficiency can improve real economic outcomes. Companies with good growth prospects see their share prices rise when markets are efficient, allowing them to raise capital and fund new projects. Companies that produce goods and services that are no longer required to see their share prices fall and the factories may be repurposed for more productive purposes, possibly leading to a merger. Furthermore, when share prices reflect more information and are more efficient, CEO decisions may improve, and they may be more prudent if active investors are monitoring them. Hedge funds also serve as a source of liquidity for other investors who need to buy or sell (e.g., to smooth out their consumption), hedge or buy insurance, or simply enjoy certain types of securities. Finally, hedge funds offer investors another source to diversify their returns.
Why should I be interested in this post?
As an investor, hedge funds may provide an opportunity to diversify its global portfolios. Including hedge funds in a portfolio can help investors obtain absolute returns that are uncorrelated with typical bond/equity returns.
For practitioners, learning how to incorporate hedge funds into a standard portfolio and understanding the risks associated with hedge fund investing can be beneficial.
Understanding if hedge funds are truly providing “excess returns” and deconstructing the sources of return can be beneficial to academics. Another challenge is determining whether there is any “performance persistence” in hedge fund returns.
Getting a job at a hedge fund might be a profitable career path for students. Understanding the market, the players, the strategies, and the industry’s current trends can help you gain a job as a hedge fund analyst or simply enhance your knowledge of another asset class.
Useful resources
Academic research
Pedersen, L. H., 2015. Efficiently Inefficient: How Smart Money Invests and Market Prices Are Determined. Princeton University Press.
Business Analysis
Wikipedia Alfred Winslow Jones
Fortune (2015) The Jones Nobody Keeps Up With (Fortune, 1966).
SEC Mutual Funds and Exchange-Traded Funds (ETFs) – A Guide for Investors.
SEC Selected Definitions of “Hedge Fund”
Credit Suisse Hedge fund strategy
Credit Suisse Hedge fund performance
Credit Suisse Long-short strategy
Credit Suisse Long-short performance benchmark
Related posts on the SimTrade blog
▶ Shruti CHAND Financial leverage
▶ Akshit GUPTA Initial and maintenance margins in futures contracts
▶ Akshit GUPTA Hedge funds
About the author
The article was written in June 2022 by Youssef LOURAOUI (Bayes Business School, MSc. Energy, Trade & Finance, 2021-2022).



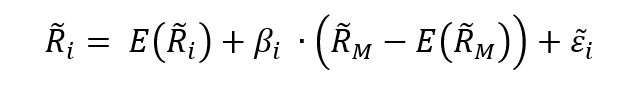
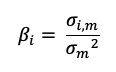
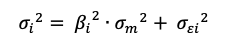
 Computation by the author (data: Bloomberg).
Computation by the author (data: Bloomberg).
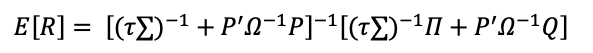
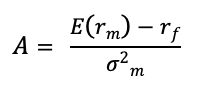
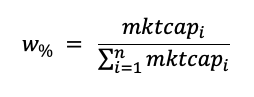
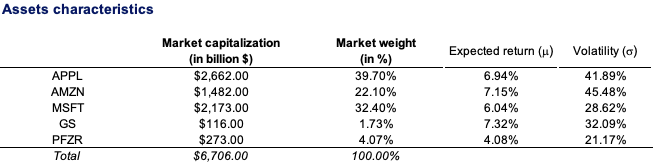
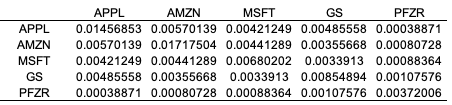

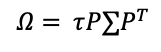
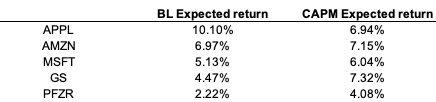
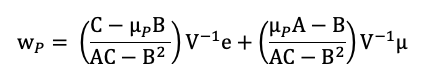
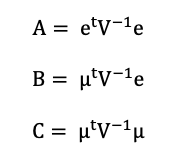
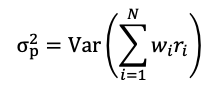
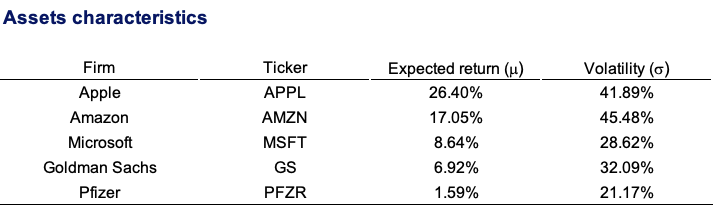

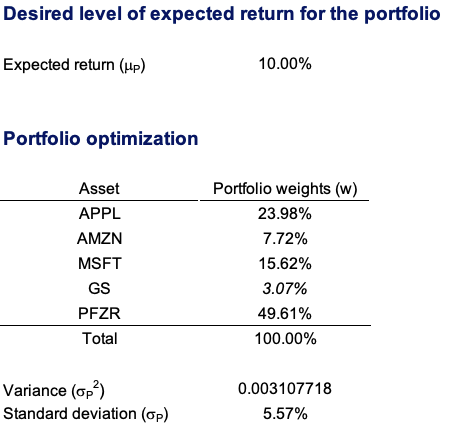
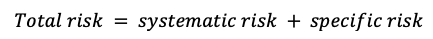
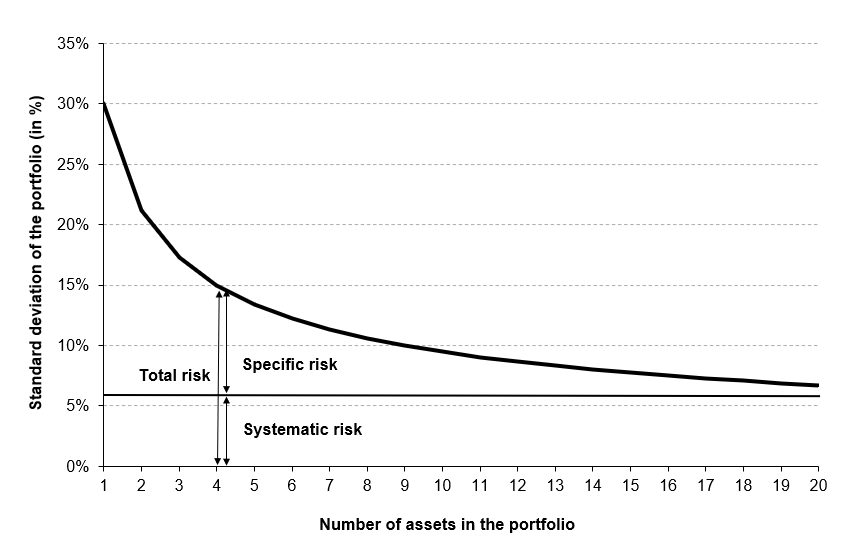
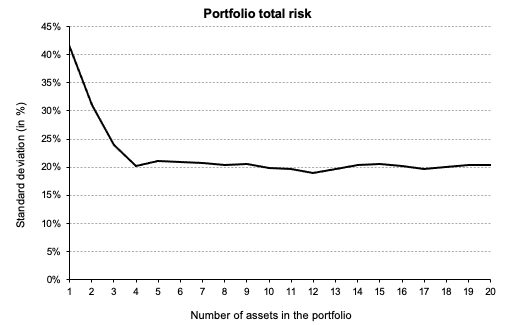 Source: Computations from the author.
Source: Computations from the author.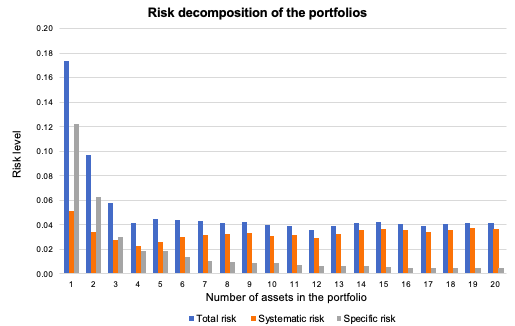 Source: Computations from the author.
Source: Computations from the author.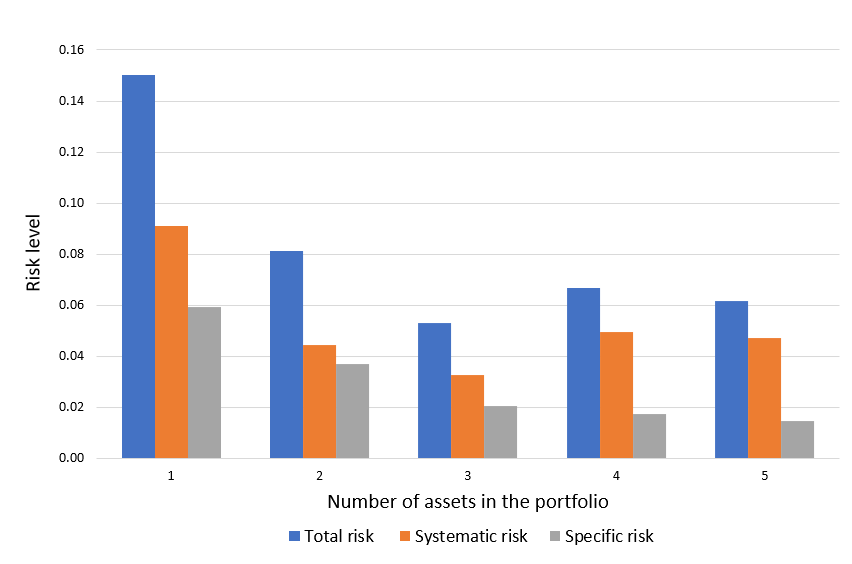 Source: Computation from the author.
Source: Computation from the author.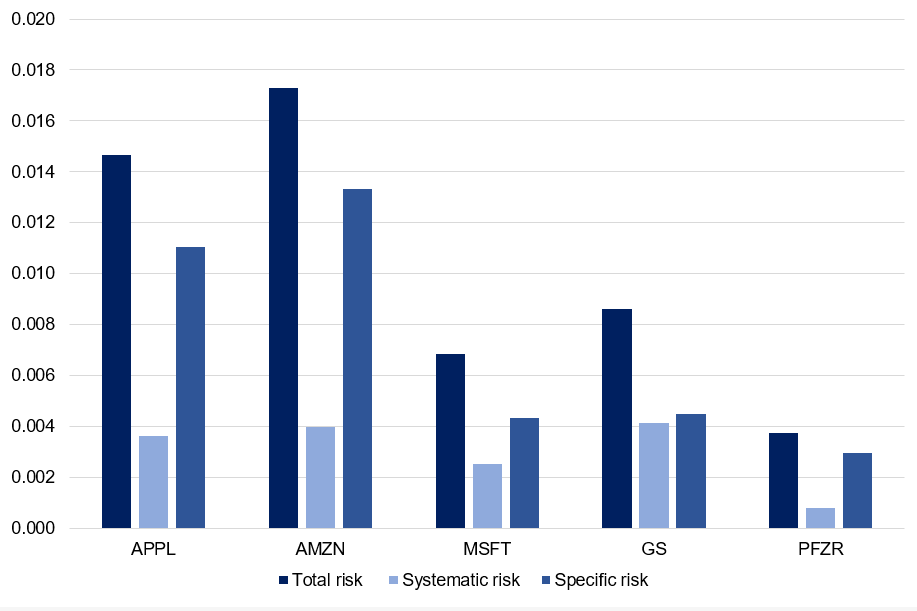 Source: Computation from the author.
Source: Computation from the author.