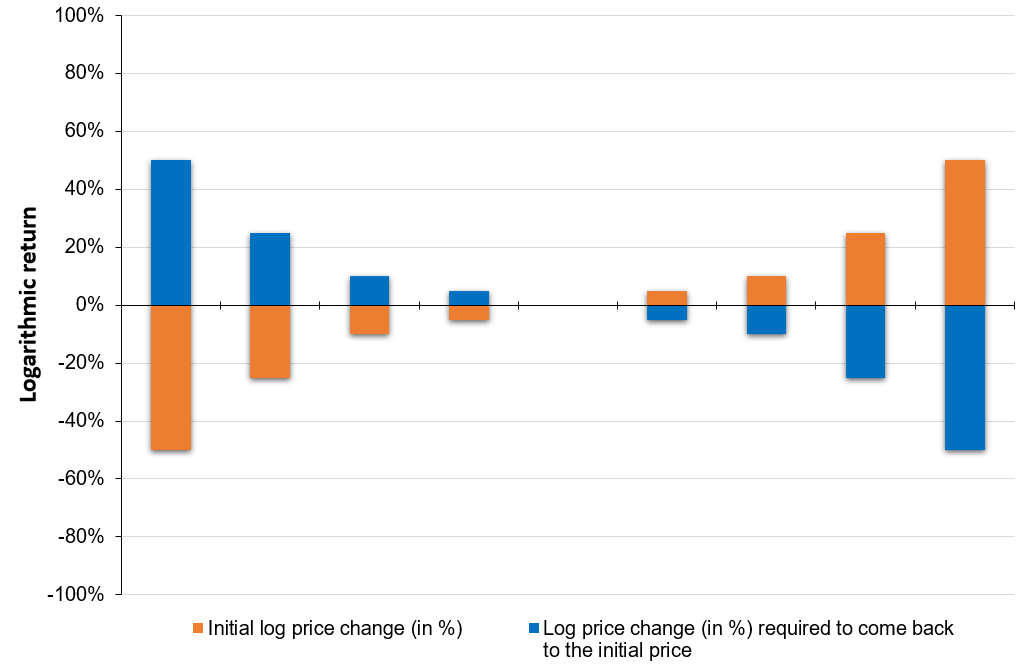
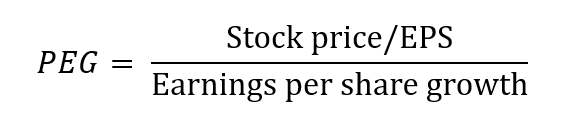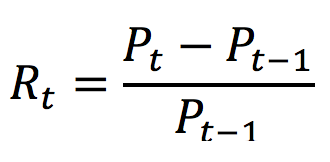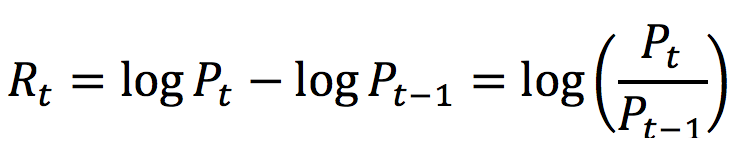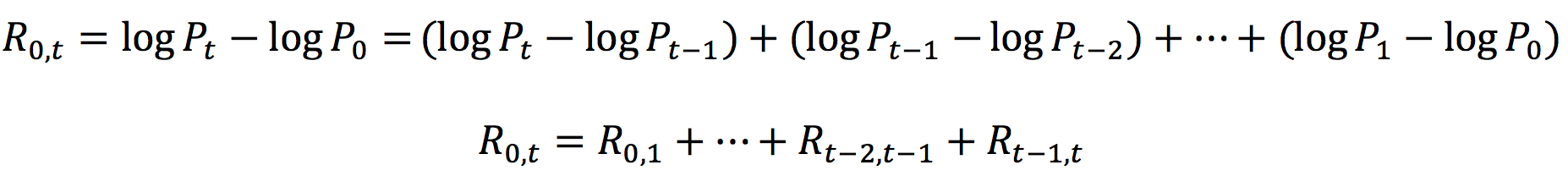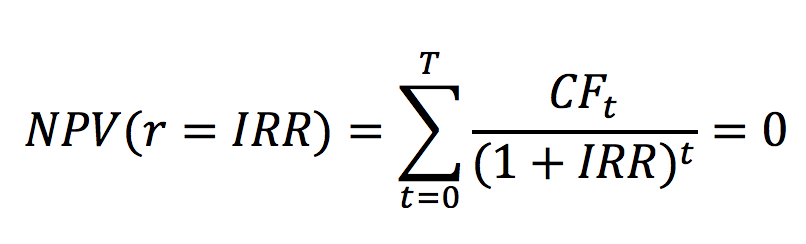In this article, Anant JAIN (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) talks about the World 10 Most Sustainable Companies in 2021.
Introduction
The Corporate Knights’ yearly list is a ranking of the 100 most sustainable companies. It is based on the analysis of companies with revenues over $1 billion (8,080 companies in 2021). This year marks the 17th year of the list.
This list is usually revealed during the World Economic Forum in Davos. The Davos Agenda is a ground-breaking gathering of world leaders to shape the values, policies, and alliances required in this difficult new environment. The World Economic Forum has been a trusted venue for leaders from business, government, international organizations, civil society, and academia to assemble at the start of each year to discuss crucial issues.
In 2021, the breakdown of the most sustainable firms by geographical areas is as follows:
- 46 in Europe
- 33 in North America
- 18 in Asia
- 2 in South America
- 1 in Africa
The top 10 most sustainable corporations of 2021 are as follows:
1. Schneider Electric SE, France
2. Orsted A/S, Denmark
3. Banco do Brazil SA, Brazil
4. Neste Oyj, Finland
5. Stantec Inc, Canada
6. McCormick & Company Inc, United States
7. Kering SA, France
8. Metso Outotec, Finland
9. American Water Works Company Inc, United States
10. Canadian National Railway Co, Canada
We detail below the characteristic of each company in the dimension of sustainability.
1. Schneider Electric SE
Industry: Electrical Equipment
Location: France
Year Founded: 1836
Schneider Electric has been named the world’s most environmentally friendly firm. This European energy and automation multinational corporation was praised for its quick and consistent response to ESG – environmental, social, and governance – issues, moving up from 29th place in 2020.
Schneider Electric is helping to reduce CO2 emissions and the rise of the Earth’s temperature by focusing on innovative and renewable alternatives. Its efforts are assisting in the prevention of global warming and the production of ecologically friendly goods that improve energy access.
The core of Schneider Electric’s strategy, according to Chair and CEO Jean-Pascal Tricoire, is to build a sustainable business and organization. Schneider has long been committed to environmental issues, and it continues to raise the bar for itself, its customers, and its partners.
2. Ørsted A/S
Industry: Electricity Generation
Location: Denmark
Year Founded: 2006
After vowing to combat climate change with renewable energy, Ørsted was voted the world’s second most sustainable company. Despite dropping to second position in 2020, the Danish power company is still the world’s most sustainable energy provider, a title it has held for three years.
The corporation, which is also renowned as one of the top renewable energy generators, has switched its operations from fossil fuels to renewable energy and has set a goal of becoming carbon neutral by 2025.
Ørsted CEO Mads Nipper said the company’s strong placement in the Global 100 report underlines both its commitment to driving a successful and sustainable business and its resolve to become a catalyst for green energy change. He also stated that in order to be effective in the fight against climate change – and to stay in business – all businesses must adopt a sustainable business model.
3. Banco do Brazil SA
Industry: Financial Services
Location: Brazil
Year Founded: 1808
Banco do Brazil, Brazil’s, and Latin America’s largest bank by assets, is also one of the most sustainable companies. The 212-year-old bank aspires to be inclusive and contribute to digitally improving society by providing internet access and supporting education by fostering innovation and motivating entrepreneurs.
In 2020, the government-owned corporation was ranked ninth, but it has quickly risen through the ranks this year.
4. Neste Oyj
Industry: Oil and Gas Industry
Location: Finland
Year Founded: 1948
Neste is a global pioneer in sustainability, with products such as renewable diesel, sustainable aviation fuel, chemical recycling to reduce plastic waste, and raw material refining innovation. The Finnish company dropped from third to fourth place in a year, but it has been on the Corporate Knights Global 100 Index for the 15th year in a row, far longer than any other global energy company.
The company’s mission of making the world a better place for our children, according to Peter Vanacker, President and CEO of Neste, drives them to strive for greater heights every day. Many companies are constantly improving their sustainability programs, making it more difficult to make the list each year. More businesses are actively implementing sustainability into their operations, which is encouraging.
5. Stantec Inc.
Industry: Engineering, Architectural Design
Location: Canada
Year Founded: 1954
Stantec is not only one of the most ecologically responsible companies in the world, but it is also a leader in North America. Clean earnings and clean investment, which are goods and services with a demonstrated environmental and social impact, accounted for half of the company’s overall score.
Gord Johnston, President and CEO of Stantec, remarked that its remarkable track record on sustainability is the result of its people’s deep commitment and good leadership throughout the company’s global operations. Its teams are striving to improve sustainability in its own operations and aiding clients in developing and achieving sustainability goals.
6. McCormick & Company Inc.
Industry: Processed & Packaged goods
Location: U.S.A.
Year Founded: 1889
McCormick & Company is not just the world’s sixth most sustainable company, but it is also the leader in the food market. Since the index’s debut five years ago, the packaged and processed foods industry in the United States has advanced 16 points to its highest position.
According to Lawrence E Kurzius, Chairman, President of McCormick & Company, it has never been more important to work together for the future of flavor and to limit its impact on the environment. The company is dedicated to producing clean revenue, providing renewable energy projects, and making the transition to 100% circular packaging.
7. Kering SA
Industry: Luxury
Location: France
Year Founded: 1963
Gucci, Saint Laurent, Bottega Veneta, Ulysse Nardin, and Pomellato’s parent business are the only luxury brands to make the top 10 sustainable companies list.
When measured against 24 quantitative key performance indicators (KPIs), including resource management, people management, financial management, clean revenue and investment, and supplier performance, Kering maintained its strong position. In order to build the future of luxury, sustainability is promoted at every level of governance, from the Board of Directors to the operational managers.
Kering’s vow to protect the environment on which it relies, according to the CEO Dr. M Sanjayan, is a big step forward for the fashion business, and it offers a massive doorway for the luxury sector to influence the people and help rethink fashion and luxury goods.
8. Metso Outotec
Industry: Industrial Machinery
Location: Finland
Year Founded: 2020
Metso Outotec is ranked 8th on the Global 100 Index, a global leader in sustainable technology and services for the recycling, aggregates, and mineral processing industries. In order to have a good impact on the globe as a sustainable leader, the Finland-based firm has set a number of lofty goals, including reducing global warming to 1.5 degrees Celsius.
Piia Karhu, Senior Vice President Business Development at Metso Outotec, remarked that their customers in the aggregates and metals and minerals industries are focused on producing sustainable goods and services. They collaborate with their customers, partners, and communities to advance sustainable innovation.
9. American Water Works Company
Industry: Utilities, Water and Wastewater
Location: U.S.A.
Year Founded: 1886
Because of its leadership and transparency, American Water is one of the top ten sustainable firms. The largest publicly listed water and wastewater utility firm in the world, founded in 1886 and employing over 6,800 people, is based in the United States.
Despite serving 15 million people in 46 states, the company saves 12.5 billion liters of water each year through efficiency measures. It has also promised to reducing greenhouse gas emissions by 40% by 2025.
10. Canadian National Railway Company
Industry: Rail Transport
Location: Canada
Year Founded: 1919
The lone railway company on the list for 2021 was the Canadian National Railway. The railway conglomerate adheres to a global standard for sustainability activities, adhering to the UN Global Compact principles and the Sustainable Development Goals of the United Nations (SDGs).
Related posts on the SimTrade blog
▶ Anant JAIN Dow Jones Sustainability Index
▶ Anant JAIN Green Investments
▶ Anant JAIN Environmental, Social & Governance (ESG) Criteria
▶ Anant JAIN The Paris Agreement
Useful resources
General resources
Corporate Knights’ Global Ranking List
The Davos Agenda
Top 10 sustainable companies
#1 Schneider Electric SE, France
#2 Orsted A/S, Denmark
#3 Banco do Brazil SA, Brazil
#4 Neste Oyj, Finland
#5 Stantec Inc, Canada
#6 McCormick & Company Inc, USA
#7 Kering SA, France
#8 Metso Outotec, Finland
#9 American Water Works Company, USA
#10 Canadian National Railway, Canada
About the author
The article was written in May 2022 by Anant JAIN (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).
▶ Read all articles by Anant JAIN.