Option Greeks – Delta

This article written by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) presents the technical subject of delta, an option Greek used in option pricing and hedging.

Introduction

Option Greeks are sophisticated financial metric used by trader to calculate the sensitivity of option contracts to different factors related to the underlying asset including the price of the underlying, its volatility, and time value. The Greeks are used as an effective tool to practice different hedging strategies and eliminate risks in a position. They also help to optimize the options positions at any point in time.

Delta is a type of option Greek which is used to compute the sensitivity or rate of change in price of the option contract with respect to the change in price of the underlying asset. It is denoted by the Greek letter (Δ). The formula for calculating the delta of an option contract is:

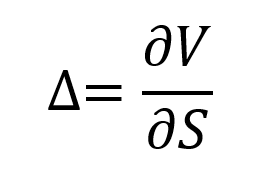
Where V is the value of the option and S the price of the underlying asset.

For example, if an option on Apple stock has a delta of 0.3, it essentially means that a $1 change in the price of the underlying asset i.e., Apple stock, will lead to a change of $0.3 in the price of the option contract.

When a trader takes a position based on the delta sensitivity of any option contract, it is called delta hedging. The goal is to achieve a delta-neutral portfolio and eliminate the risks associated with movement in the prices of the underlying. Due to the complexity of the tool, delta hedging is generally practiced by professional traders in large financial institutions. In options, the delta of any call option is always positive whereas the delta of a put option is always negative.

Delta formula

Call option

According the Black-Scholes-Merton model, the formula for calculating the delta for a European-style call option on a non-dividend paying stock is given by:

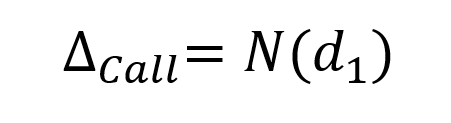
Where N represents the cumulative distribution function of the normal distribution and d₁ is given by:

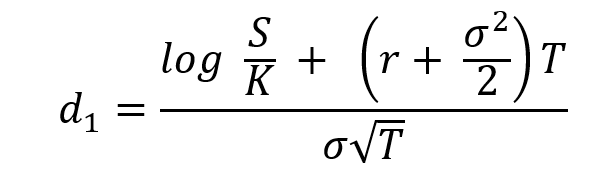
Where S is the price of the underlying asset (at the time of valuation of the option), σ the volatility in the price of the underlying asset, T time to maturity of the option, K the strike price of the option, and r the risk-free rate of return.

Put option

According the Black-Scholes-Merton model, the formula for calculating the delta for a European-style put option on a non-dividend paying stock is given by:

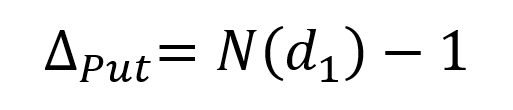
Delta as a function of the price of the underlying asset

Call option

The delta as a function of the price of the underlying asset for a European-style call option is represented in Figure 1.

Figure 1. Delta of a call option.

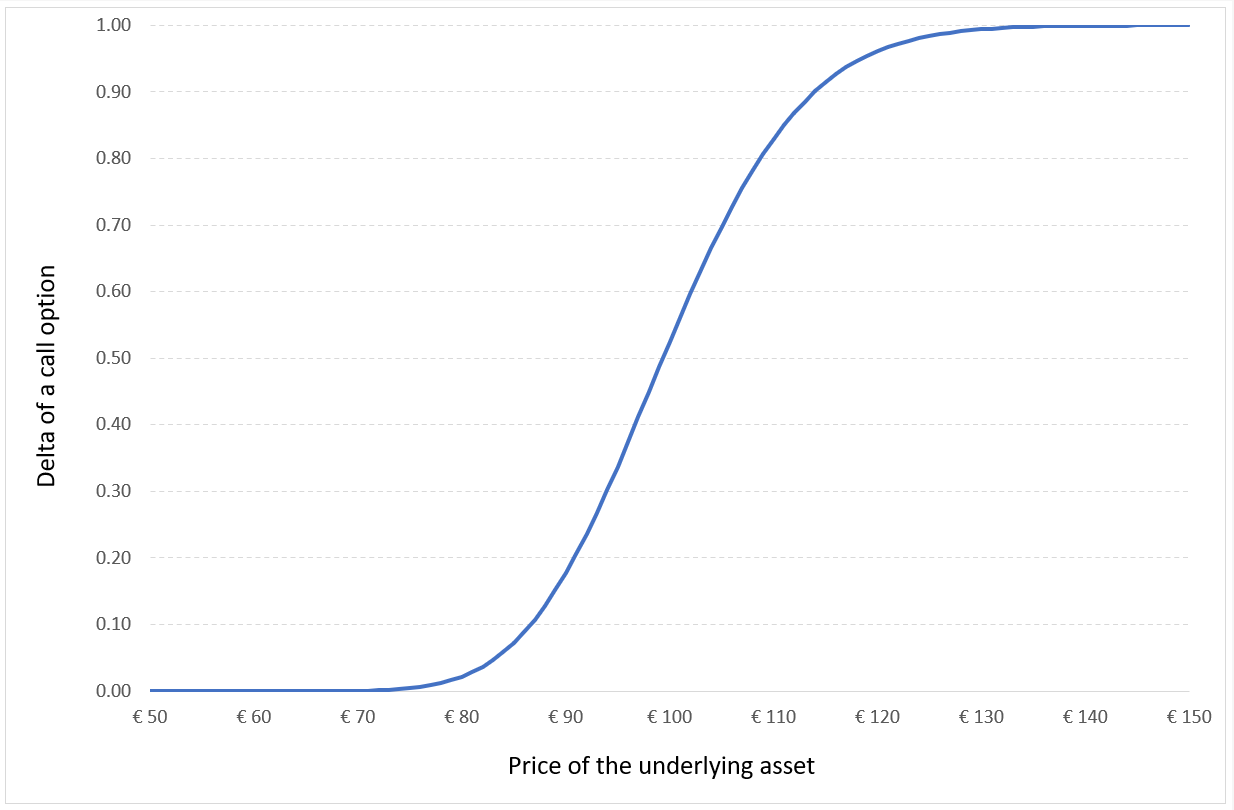
Source: computation by the author (Model: Black-Scholes-Merton).

For a call option, the delta increases from 0 (out-of-the-money option) to 1 (in-the-money option).

Put option

The delta as a function of the price of the underlying asset for a European-style put option is represented in Figure 2.

Figure 2. Delta of a put option.

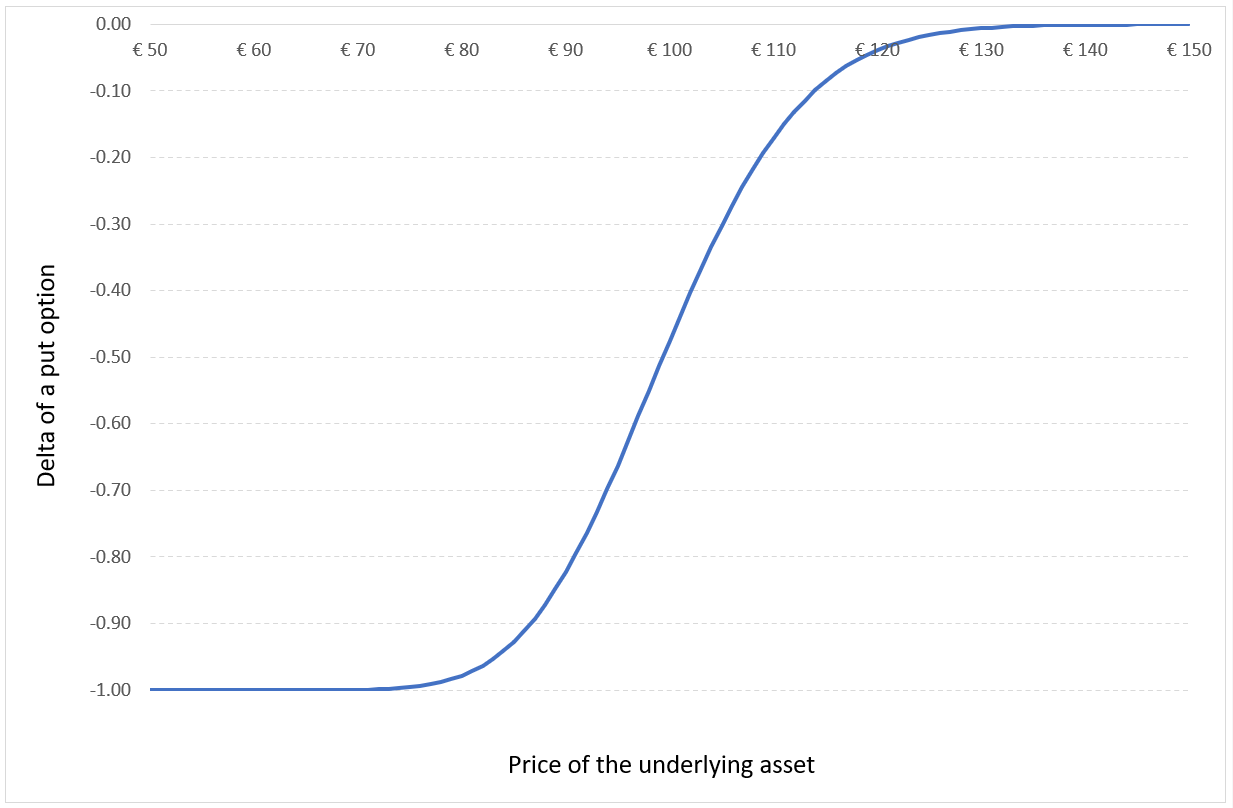
Source: computation by the author (Model: Black-Scholes-Merton).

For a put option, the delta increases from -1 (in-the-money option) to 0 (out-of-the-money option).

Excel pricer to calculate the delta of an option

You can download below an Excel file for an option pricer (based on the Black-Scholes-Merton or BSM model) which allows you to calculate the delta of a European-style call option.

Delta Hedging

A trader holding an option contract uses delta hedging to offset the risks associated with the price movement in the underlying asset by continuously buying and selling the underlying asset to achieve delta neutrality. This is used by option traders in financial institutions to manage their option book (the delta is computed at the option level and aggregated at the book level) and generate the margin the bank of the option writing activity.

The delta of an option contract keeps on changing as the prices of the underlying and the option contract changes. So, to maintain the delta neutrality the trader must constantly monitor the markets and execute trades to achieve neutrality. The process of continuously buying or selling the underlying asset is called dynamic hedging in options.

At the first order, the change of the value of a delta-hedged call option over the period from t to t+ δt would be equal to the risk-free rate (r) over the period:

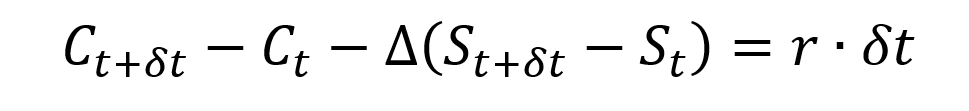
Limitations of delta hedging

Although delta hedging is a useful tool to offset the risks associated to the movement in the price of an underlying, it comes with some limitations which are:

Transaction cost

Since delta hedging requires constantly buying or selling the underlying asset, it comes with a high transaction cost. This makes delta hedging an expensive tool to optimize the portfolio against price risk. In practice, traders would adjust their option position from time top time.

Illiquid Markets

When the market for an asset is illiquid, it is difficult to practice delta hedging as the trader will not be able to constantly buy or sell the underlying asset to neutralize the price impact.

Example for calculating delta

Let us consider a call option contract with the following characteristics: the underlying asset is an Apple stock, the option strike price (K) is equal to $300 and the time to maturity (T) is of one month (i.e., 0.084 years).

At the time of valuation, the price of the Apple stock (S) is $300, the volatility (σ) of Apple stock is 30% and the risk-free rate (r) is 3% (market data).

The delta of a call option is approximately equal to 0.50238.

Using the above value, we can say that due to a $1 change in the price of the underlying asset, the price of the option will change by $0.50238.

Related posts on the SimTrade blog

   ▶ All posts about Options

   ▶ Akshit GUPTA Options

   ▶ Akshit GUPTA History of Options markets

   ▶ Akshit GUPTA Option Trader – Job description

Option pricing and Greeks

   ▶ Jayati WALIA Black-Scholes-Merton option pricing model

   ▶ Akshit GUPTA Option Greeks – Gamma

   ▶ Akshit GUPTA Option Greeks – Theta

   ▶ Akshit GUPTA Option Greeks – Vega

Useful resources

Research articles

Black F. and M. Scholes (1973) The Pricing of Options and Corporate Liabilities The Journal of Political Economy, 81, 637-654.

Merton R.C. (1973) Theory of Rational Option Pricing Bell Journal of Economics, 4(1): 141–183.

Books

Hull J.C. (2015) Options, Futures, and Other Derivatives, Ninth Edition, Chapter 19 – The Greek Letters, 424 – 431.

Wilmott P. (2007) Paul Wilmott Introduces Quantitative Finance, Second Edition, Chapter 8 – The Black Scholes Formula and The Greeks, 182-184.

About the author

Article written in August 2021 by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).