Gold resources in the world
In this article, Nithisha CHALLA (ESSEC Business School, Grande Ecole Program – Master in Management (MiM), 2021-2024) presents how gold production, reserves, and investments play a crucial role in national economies and global financial markets.
Introduction
Gold has been used for ornaments, jewelry, and religious artifacts since prehistoric times. Gold is found in various geological environments, including alluvial deposits, quartz veins, and sulfide ores. The formation process involves hydrothermal fluids depositing gold in the earth’s crust. The top gold-producing countries include China, Australia, Russia, the United States, and Canada. These nations contribute significantly to global gold production. The World Gold Council tracks these reserves, which are critical to national economic stability.
Global distribution of major gold-producing countries in the world
The top 3 gold-producing countries are China, Australia and Russia. These countries mine gold in large quantities and contribute significantly to global gold production. Gold mining is a significant industry in many countries, contributing to employment, infrastructure development, and economic growth.
Global Gold Production by Country in 2020
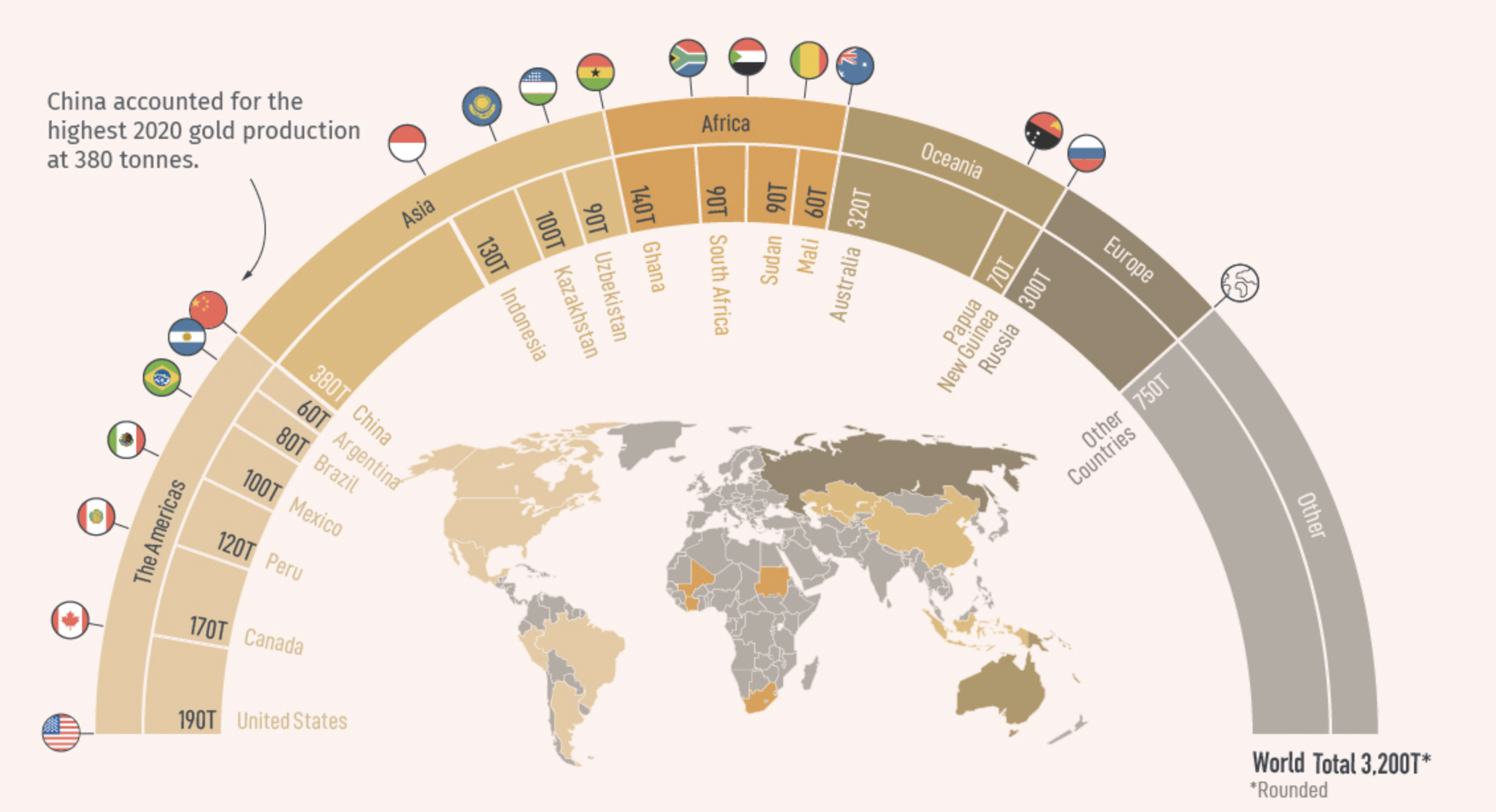
Source: Visual Capitalist
Global Gold Production by Country in 2020 by table

Source: Visual Capitalist
China
China has been the world’s largest gold producer since 2007, contributing to nearly 12% of global production. The government tightly controls the country’s gold industry, and the People’s Bank of China is a major buyer of domestically produced gold, reinforcing its role as a strategic economic asset. The Chinese government encourages gold production as part of its broader strategy to diversify its foreign exchange reserves and reduce dependency on the U.S. dollar.
China’s Gold Production in last 10 years
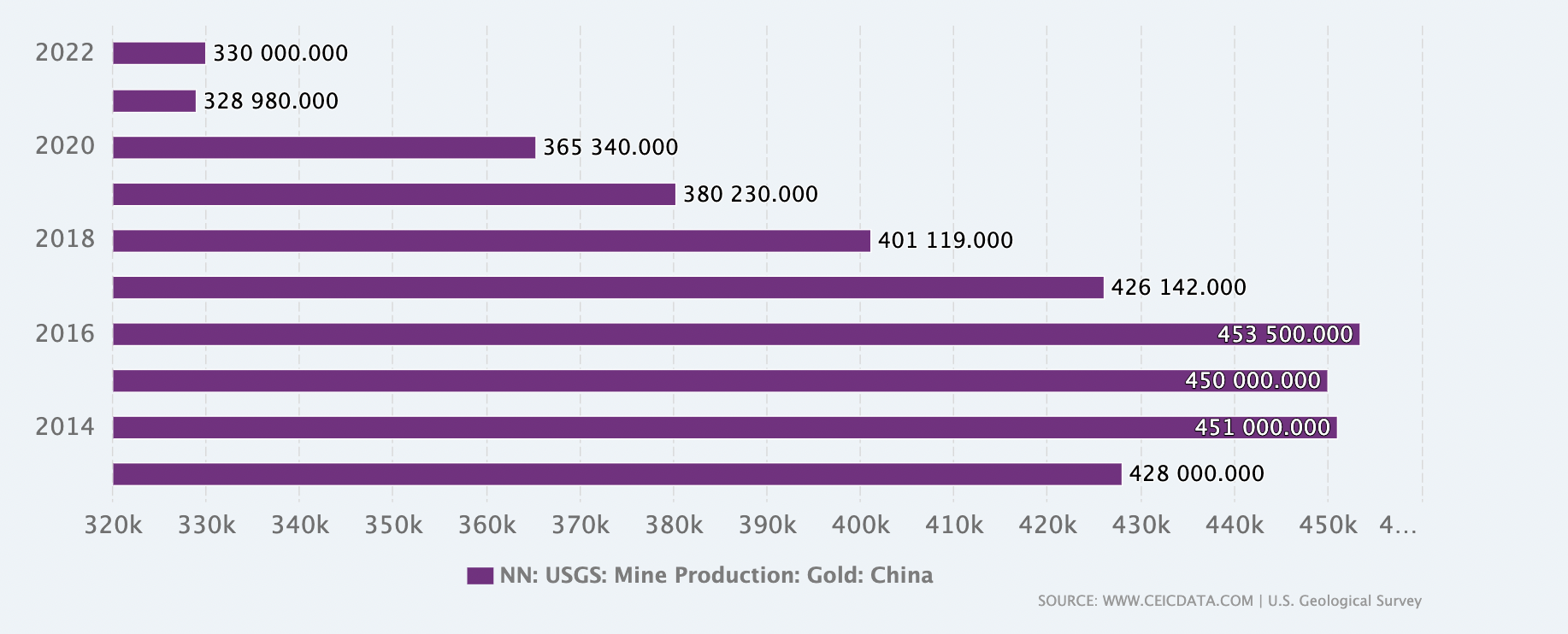
Source: CEIC Data
Australia
Australia is the second-largest gold producer, with significant mining operations in Western Australia. The country’s gold industry is a crucial part of its economy, contributing billions to GDP and employing thousands. Gold exports are a major source of foreign revenue, and companies like Newcrest Mining and Northern Star Resources are key players. Australia’s stable political environment and favorable mining regulations make it an attractive destination for global investment in gold mining.
Australia’s Gold Production in last 10 years
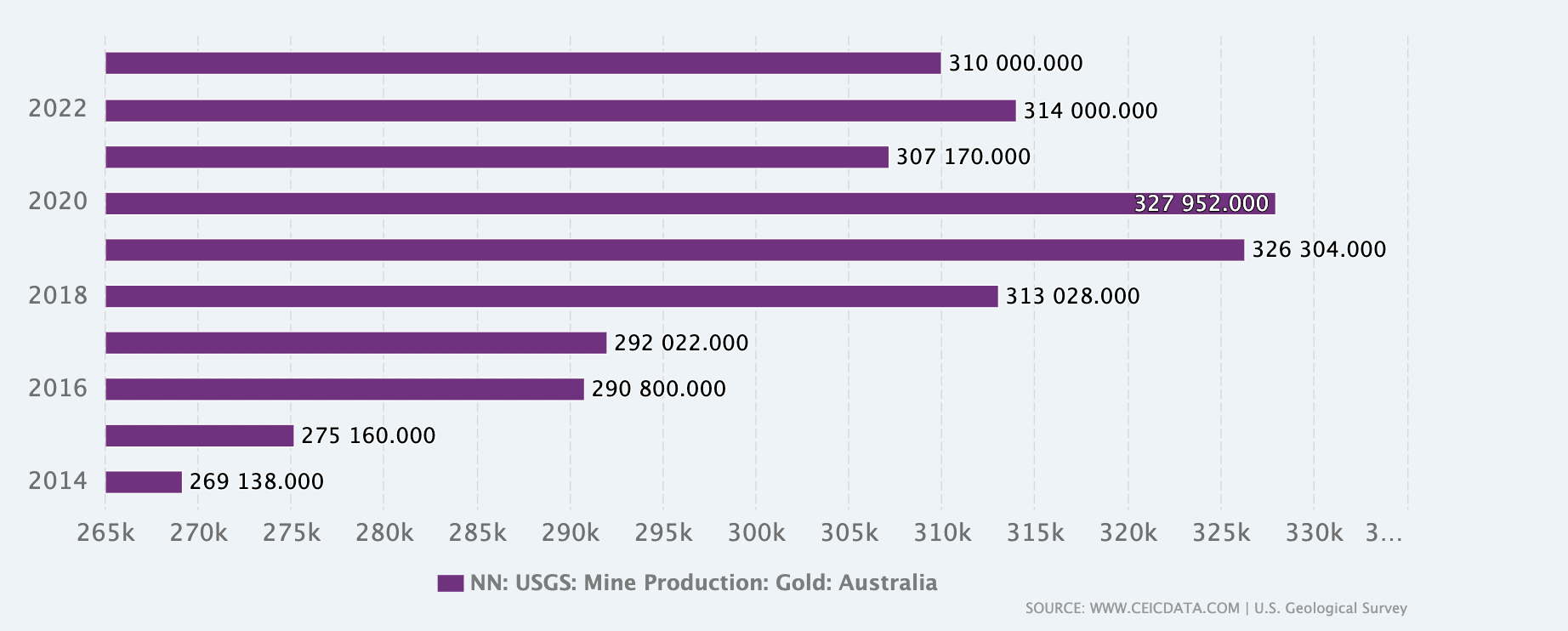
Source: CEIC Data
Russia
Russia is another leading gold producer, with significant reserves in Siberia and the Far East. The Russian government views gold as a critical asset for economic security, especially in light of Western sanctions. The Central Bank of Russia has been steadily increasing its gold reserves, positioning gold as a hedge against geopolitical risks and currency fluctuations.
Russia’s Gold Production in last 10 years
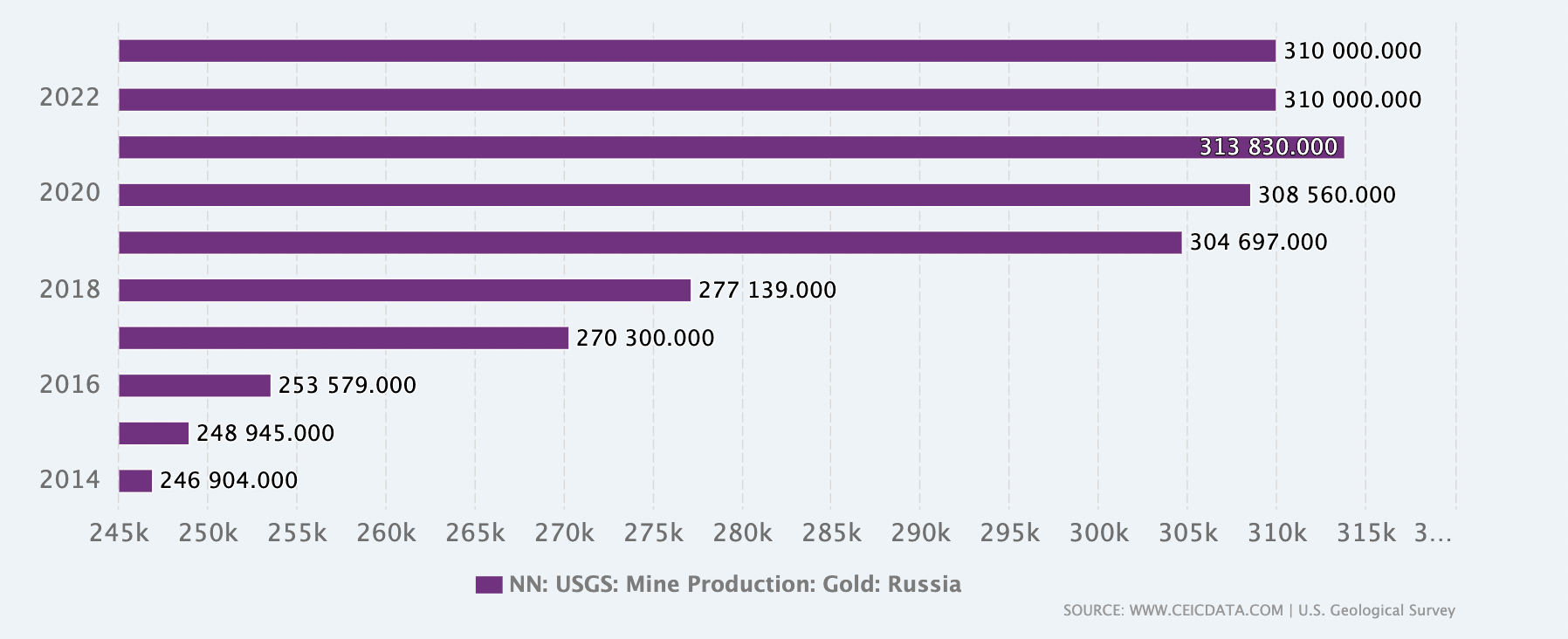
Source: CEIC Data
Geological Formation and Economic Viability
Economic Geology of Gold
Gold is found in various geological settings, including orogenic belts, volcanic arcs, and sedimentary basins. The economic viability of a gold deposit depends on its grade, size, and accessibility. High-grade deposits, such as those found in the Witwatersrand Basin in South Africa, are particularly valuable due to their high gold content per ton of ore.
Exploration and Development Costs
The process of discovering and developing a gold mine is capital-intensive. Exploration costs can run into millions of dollars, with no guarantee of success. Once a deposit is confirmed, the costs of development, including building infrastructure and obtaining permits, can be significant. The economic feasibility of a project is assessed through metrics like the internal rate of return (IRR) and net present value (NPV), which consider future cash flows and the cost of capital.
Types of Gold Deposits and Financial Implications
Primary Deposits and Investment Strategies
Primary gold deposits are often found in lode and vein formations. These deposits require underground mining, which is more expensive and complex than surface mining. Companies must carefully assess the financial risks associated with developing these types of deposits, including the potential for fluctuating gold prices, which can affect profitability.
Case study 1: According to Andrew Watson working at Geology of Investors, Barrick Gold’s operations in Nevada, particularly the Carlin Trend, represent one of the largest concentrations of high-grade gold in the world. The financial success of these operations is due to a combination of rich deposits and efficient mining practices. The Carlin Trend’s production has contributed significantly to Barrick’s bottom line, making it a cornerstone of the company’s global portfolio.
Secondary deposits and economic access
Placer gold deposits, found in riverbeds and alluvial plains, are easier and less costly to mine. These deposits were the target of historical gold rushes, such as the California Gold Rush and the Klondike Gold Rush. Placer mining is typically associated with small-scale operations, but larger companies may also exploit these resources when they are economically viable.
Case study 2: In regions like Africa and South America, placer gold mining is often a critical source of income for local communities. However, these operations can be risky due to fluctuating gold prices and the informal nature of many small-scale mining enterprises. According to Luca Raineri from IAI (Instituto Affari Internazionali), “the amount of gold illegally smuggled out of the Sahara-Sahel region is reportedly much greater than that smuggled out of the Great Lakes region, and its aggregate economic value higher than that of drug or migrant smuggling (Micallef et al. 2019; Hunter 2019). Politicization may explain the much greater attention dedicated to drug and migrant smuggling in the Sahara-Sahel and gold smuggling in the Great Lakes region.”
Tertiary deposits and unconventional gold resources
As traditional gold resources become scarcer, companies are exploring unconventional sources, such as seabed mining (also known as deep-sea mining, which is the process of extracting minerals from the ocean floor). These projects involve significant financial risk due to the high cost of deep-sea exploration and extraction. However, if successful, seabed mining could unlock vast new resources, potentially reshaping the global gold market.
Case study 3: Nautilus Minerals attempted to pioneer seabed mining with the Solwara 1 project off the coast of Papua New Guinea. Despite initial optimism, the project faced numerous financial and technical challenges, ultimately leading to the company’s bankruptcy. Gary Juffa, governor of Oro province, had questioned Pala in parliament saying, “In fact, developed nations have banned seabed mining or have spoken against it because experts and scientists have stated that the unknowns are too great to ignore, Leaders of coastal communities, if you do not stop this and do not watch this with concern, then you are failing your people.”
Gold Reserves and Their Economic Significance
Global Gold Reserves
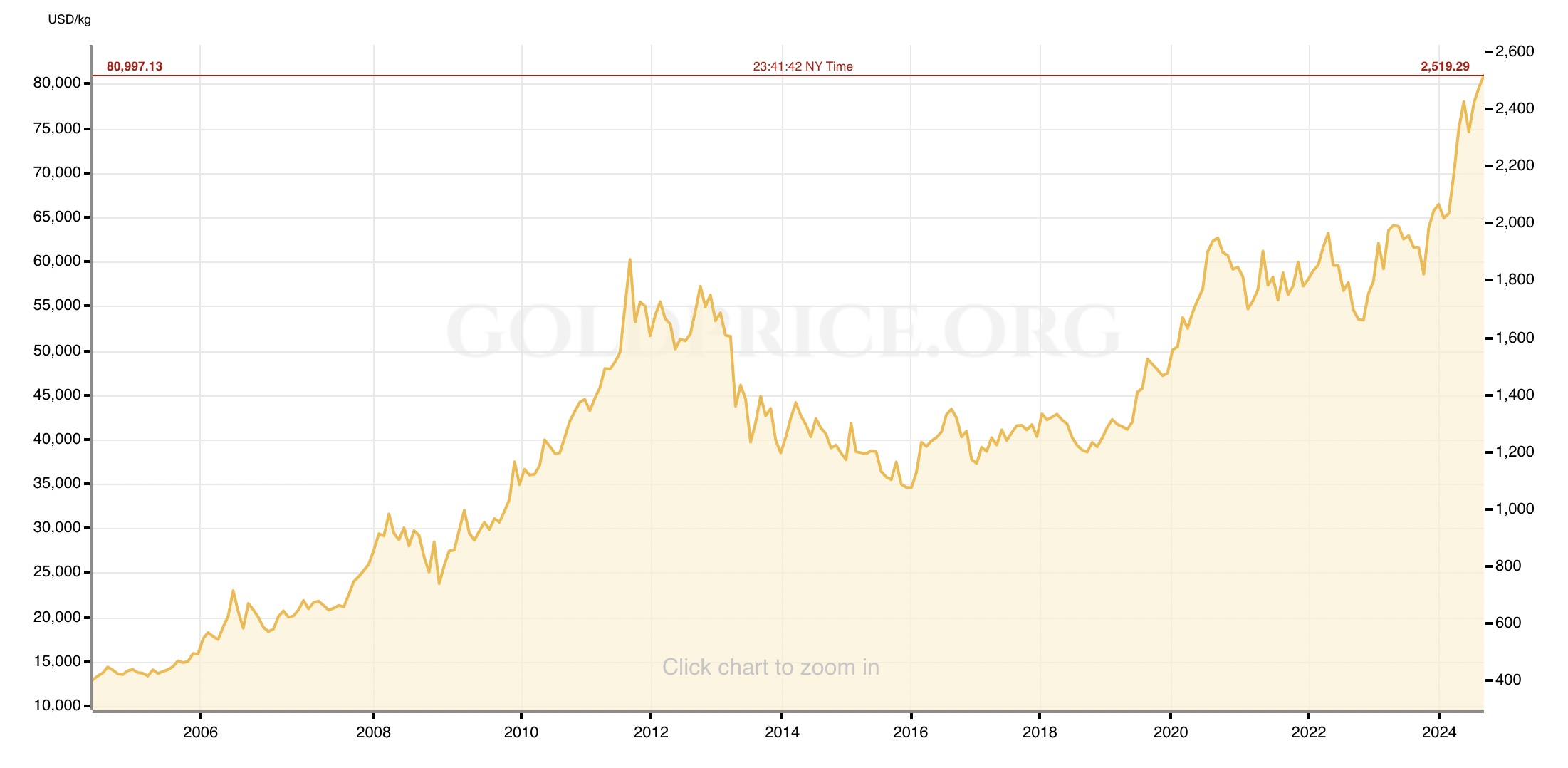
Central Banks and Sovereign Wealth: Central banks hold significant gold reserves as part of their foreign exchange holdings. Gold serves as a hedge against inflation and currency risk, providing economic stability in times of financial uncertainty. Countries like the United States, Germany, and Italy have some of the largest gold reserves, which play a crucial role in their monetary policy.
Example – India’s Gold Reserves: India, with its deep cultural affinity for gold, also holds significant gold reserves. The Reserve Bank of India (RBI) has historically used gold as a key asset in its foreign exchange reserves. During the 1991 balance of payments crisis, India famously pledged part of its gold reserves to secure an IMF loan, highlighting the strategic importance of gold in national economic policy.
Gold as a Hedge and Investment Asset
Gold ETFs and Financial Markets: Gold exchange-traded funds (ETFs) have revolutionized how investors access the gold market. ETFs like SPDR Gold Shares (GLD) allow investors to buy shares that are backed by physical gold, offering a liquid and convenient way to invest in the metal. The rise of gold ETFs has significantly impacted the global gold market, influencing prices and investment flows.
Example – The Role of Gold in Portfolio Diversification: Financial advisors often recommend gold as part of a diversified investment portfolio. During periods of economic instability, such as the 2008 financial crisis, gold tends to perform well as a safe haven asset. Studies have shown that adding gold to a portfolio can reduce risk and enhance returns, particularly in volatile markets.
Conclusion
This article expands a detailed view of the economic and financial characteristics of global gold resources. It includes detailed case studies and examples, illustrating how gold production, reserves, and investments play a crucial role in national economies and global financial markets.
Why should I be interested in this post?
Gold has been used to maintain economic stability, especially during times of hyperinflation or economic collapse. Studying historical examples of this helps students analyze how governments can use resources to stabilize economies and maintain public confidence in financial systems.
Related posts on the SimTrade blog
▶ Nithisha CHALLA History of Gold
▶ Nithisha CHALLA Gold mines and their story
Useful resources
Wikipedia Gold
Geology of Investors Elephants in the Nevada Desert: Carlin-type Gold Deposits
IAI(Instituto Affari Internazionali) Gold Mining in the Sahara-Sahel: The Political Geography of State-making and Unmaking
Only gold A Brief History of Gold
Mongabay Deep-sea mining project in PNG resurfaces despite community opposition
About the author
The article was written in September 2024 by Nithisha CHALLA (ESSEC Business School, Grande Ecole Program – Master in Management (MiM), 2021-2024).