Understanding the Gordon-Shapiro Dividend Discount Model: A Key Tool in Valuation
In this article, Isaac ALLIALI (ESSEC Business School, Bachelor in Business Administration (BBA), 2019-2023) explains about the Gordon-Shapiro Dividend Discount Model, which is a key tool in valuation.
Introduction
The Gordon-Shapiro Dividend Discount Model, also known as the Gordon-Shapiro formula and the Gordon Growth Model, is a central tenet in finance. It provides investors and financial analysts a simple tool to value a company based on its future dividends that are expected to remain at a constant growth rate. This model was named after economists Myron J. Gordon and Eli Shapiro, who developed it.
The Gordon-Shapiro formula
The Gordon-Shapiro formula is articulated through a relatively simple equation:
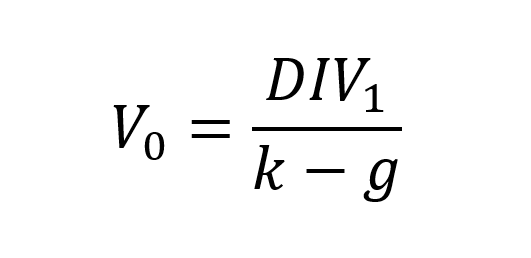
where:
V stands for the value of the stock.
DIV
k is the investor’s required rate of return.
g is the constant growth rate of dividends.
This formula is premised on the idea that a company’s stock is worth the present value of all its future dividends.
Proof of the Gordon-Shapiro formula
To understand the derivation of the formula, let us consider a perpetuity model for valuing stocks. In a perpetuity model, the value of an asset is determined by the discounted value of its future cash flows. In the case of stocks, dividends represent the cash flows received by investors (shareholders or stockholders).
Assuming that the company pays a constant dividend indefinitely, the present value of the future dividends can be expressed as follows:
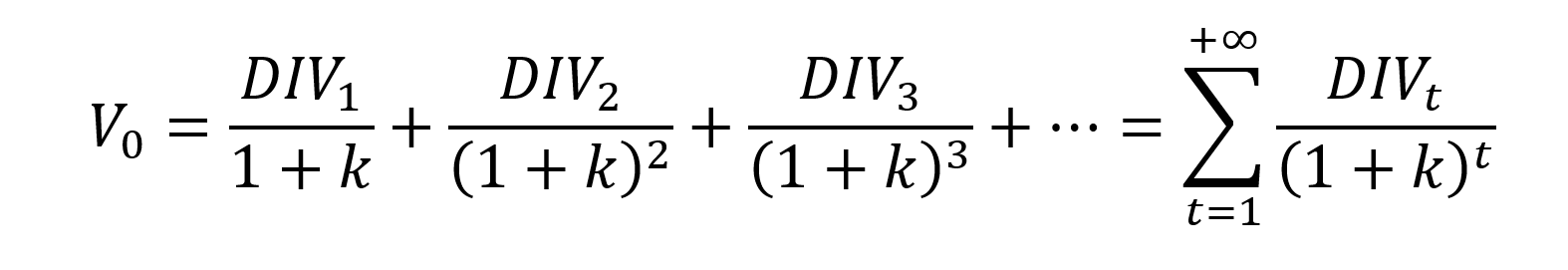
where DIV1, DIV2, DIV3 and so on, represent the expected dividends in subsequent periods.
To simplify the formula, we assume that the dividend grows at a constant rate (g). This means that each subsequent dividend can be expressed as a multiple of the previous dividend:
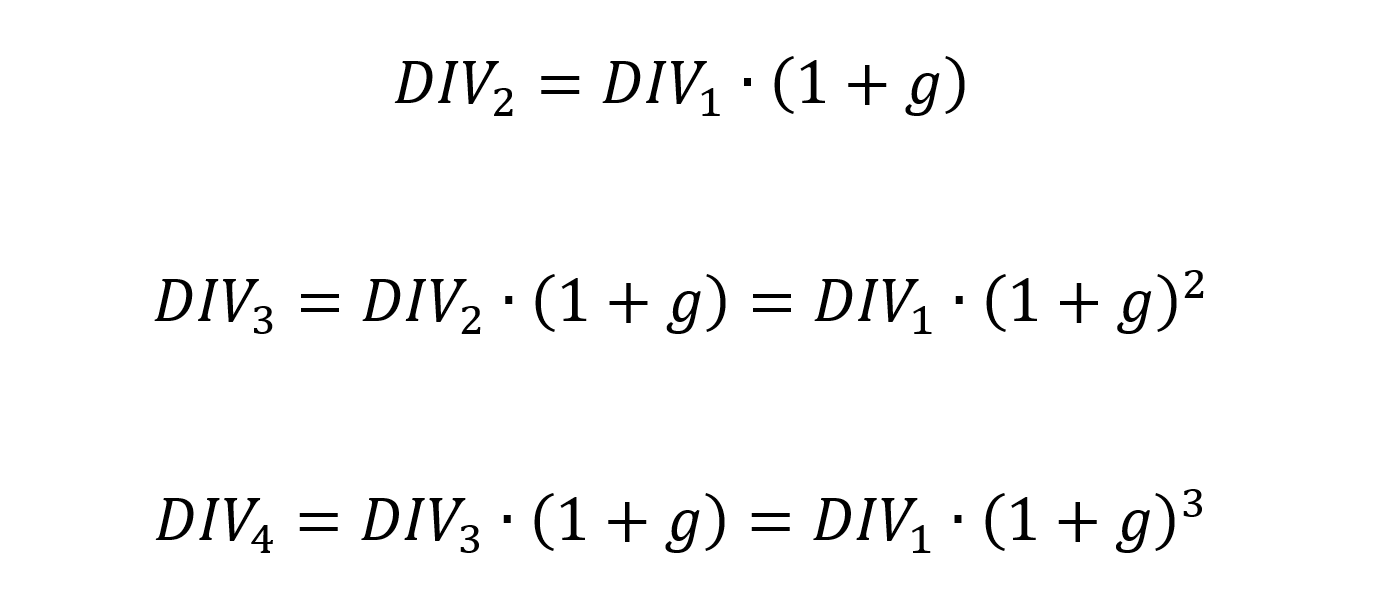
Substituting these dividend expressions into the perpetuity formula, we have:
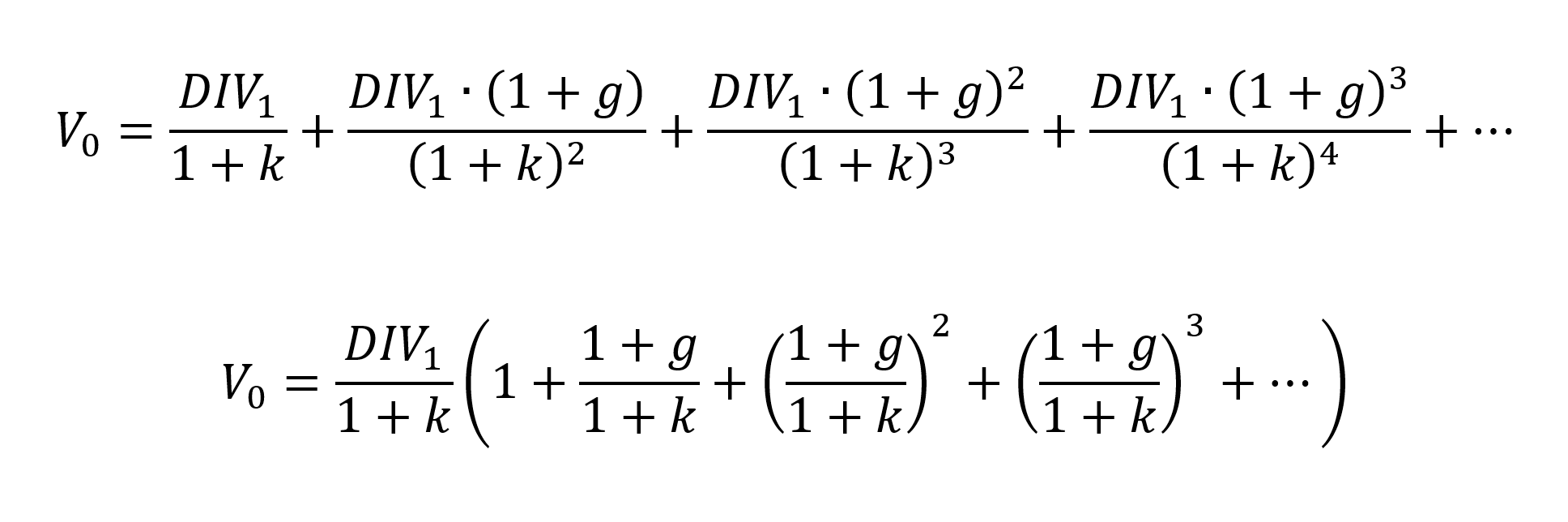
Inside the parentheses, we recognize an infinite geometric series with a ratio q equal to (1+g)/(1+k) for the geometric sequence.
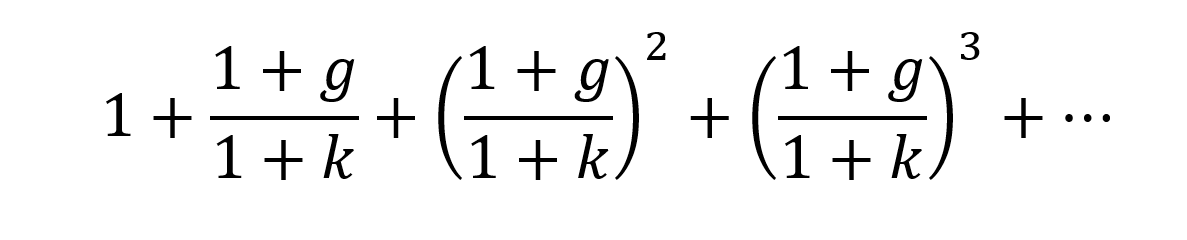
The sum of an infinite geometric series denoted by S with a ratio q is equal to 1/(1-q). Applied to the case above, we obtain:
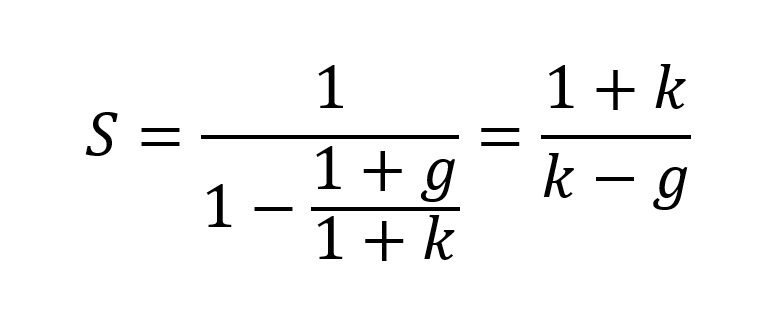
This leads to the Gordon Shapiro formula:
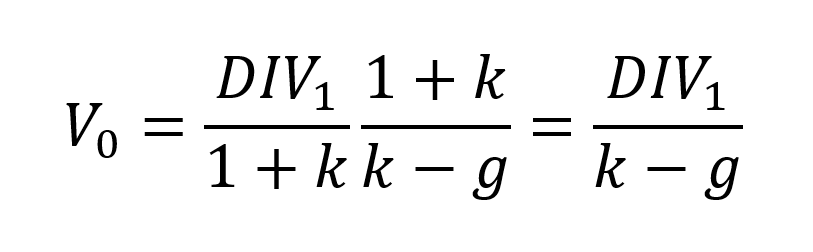
Simplifying further:
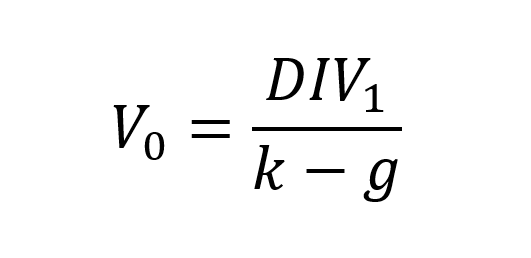
Therefore, the Gordon-Shapiro formula for estimating the intrinsic value of a stock is derived.
Assumptions of the Gordon Growth Model
The Gordon-Shapiro Dividend Discount Model is based on several key assumptions:
Constant Growth Rate: the model assumes that dividends grow at a constant rate indefinitely.
Required Rate of Return: the required rate of return exceeds the dividend growth rate. This condition is necessary for the formula to work.
Dividends: the company is expected to distribute dividends.
While these assumptions may not hold in all cases, they offer a starting point for the valuation process.
Applicability of the Gordon Growth Model
The Gordon Growth Model is especially useful in certain scenarios. For example, it is an excellent tool when assessing companies with stable growth rates, such as utility companies or large, mature firms.
However, the model has limitations when used for companies that don’t pay dividends or those with a dividend growth rate that is not consistent. High-growth companies, for instance, reinvest their profits for expansion rather than paying dividends. Similarly, companies facing fluctuating growth rates may present challenges for the model’s assumptions.
Example
After researching Pfizer’s data, we assume that this company pays an annual dividend per share (DPS) of $0.40. The required rate of return (k) for the company’s stock 9,16% was computed with the CAPM Model under the following assumptions: (Risk free rate of return= 4,73%; Beta of Pfizer stock is 0,62 and Market rate of return =11,88%), and the expected growth rate of dividends (g) is 6,40%.
Using the Gordon Shapiro formula:
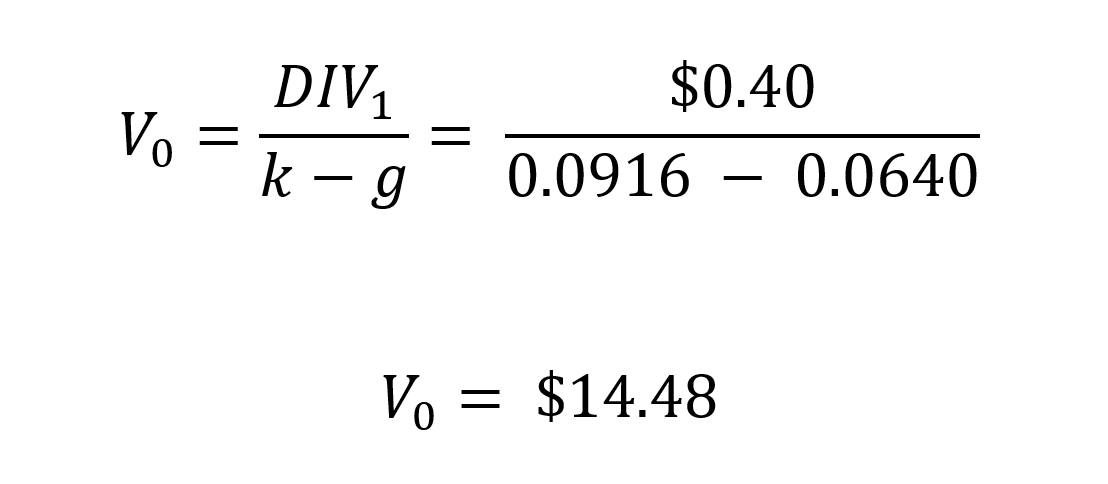
In this example, based on the given assumptions, the Gordon Shapiro model estimates the intrinsic value (V0) of Pfizer’s stock to be $14.48 per share. The current market price of Pfizer’s stock ($37,60) is significantly higher than the estimated intrinsic value, it could suggest that the stock is potentially overvalued. This may indicate a cautionary signal for investors, as it implies that the stock’s market price may not be justified by the projected dividends and required rate of return. It’s important to note that the Gordon Shapiro model is a simplified valuation tool and relies on various assumptions. The actual value of a stock is influenced by numerous factors, including market conditions, company performance, industry trends, and investor sentiment. Investors should conduct further research, analyze additional factors, and seek professional advice before making investment decisions based solely on the findings of the Gordon Shapiro model or any other valuation model.
Conclusion
Despite its limitations, the Gordon-Shapiro Dividend Discount Model remains a valuable tool in financial analysis and investment decision-making. Its simplicity and focus on dividends make it an attractive model for investors, especially when applied appropriately and in the right context. Investors and financial analysts alike should understand this model as part of their toolkit for assessing a company’s inherent value.
Related posts on the SimTrade blog
▶ William LONGIN How to compute the present value of an asset?
▶ Maite CARNICERO MARTINEZ How to compute the net present value of an investment in Excel
▶ Pranay KUMAR Time is money
Useful resources
SimTrade course Financial analysis
Gordon, Myron J., and Eli Shapiro (1956) “Capital Equipment Analysis: The Required Rate of Profit.” Management Science, 3(1): 102-110.
About the author
The article was written in June 2023 by Isaac ALLIALI (ESSEC Business School, Bachelor in Business Administration (BBA), 2019-2023).

