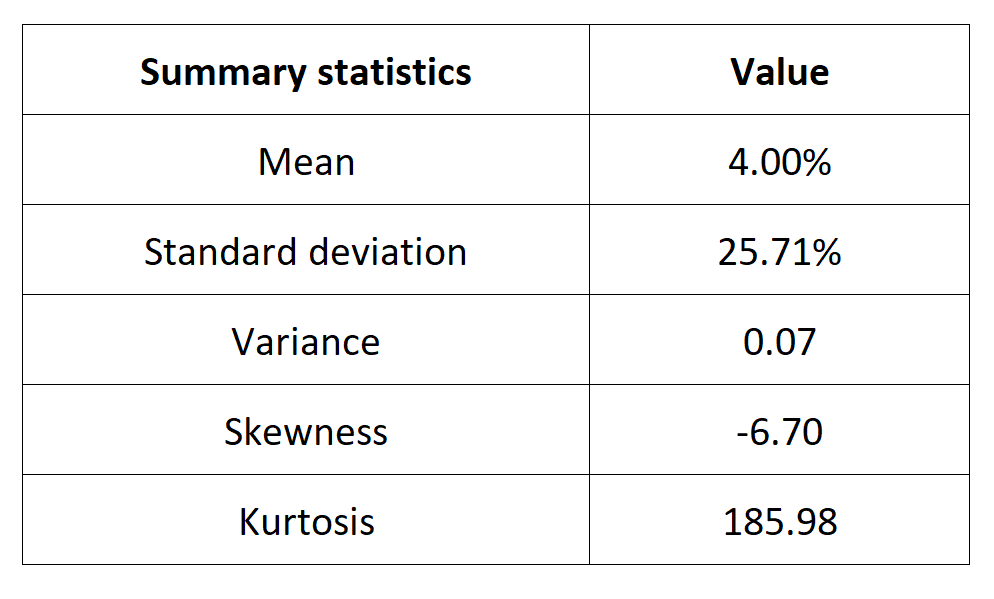
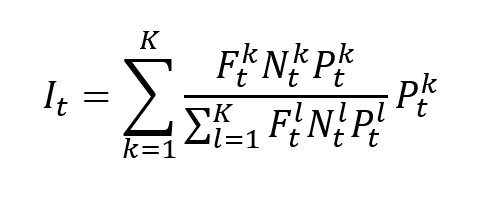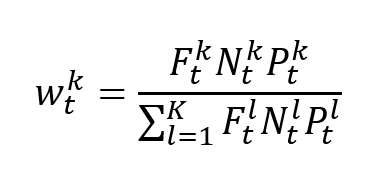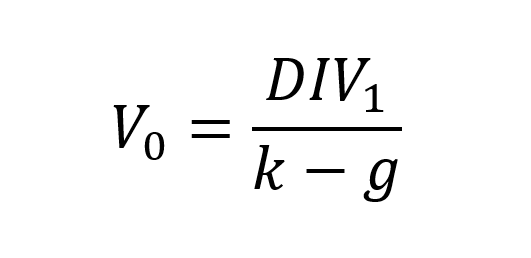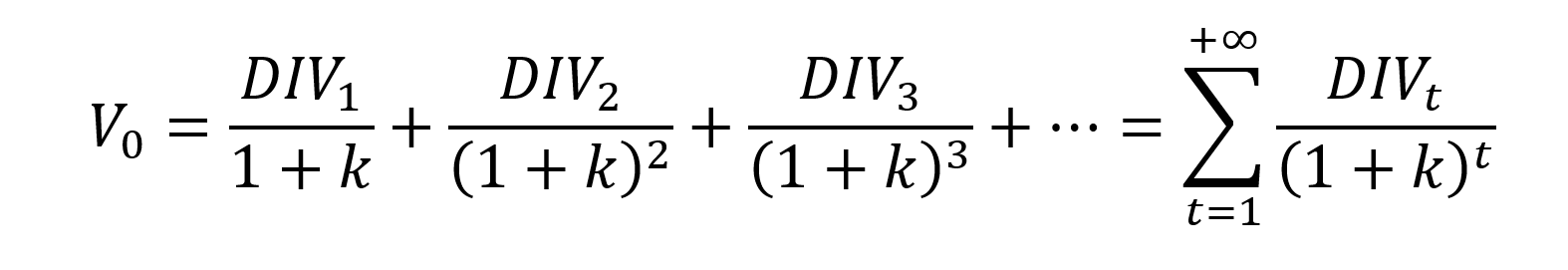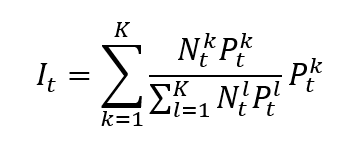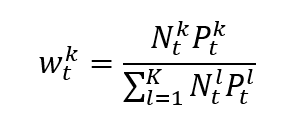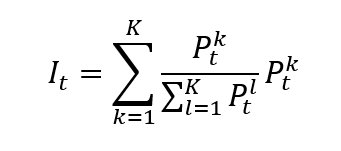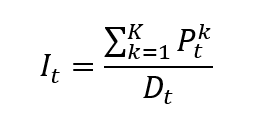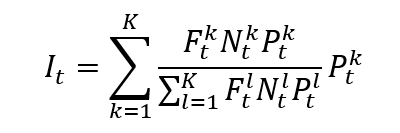How to get crypto data
In this article, Snehasish CHINARA (ESSEC Business School, Grande Ecole Program – Master in Management, 2022-2024) explains how to get crypto data.
Types of data
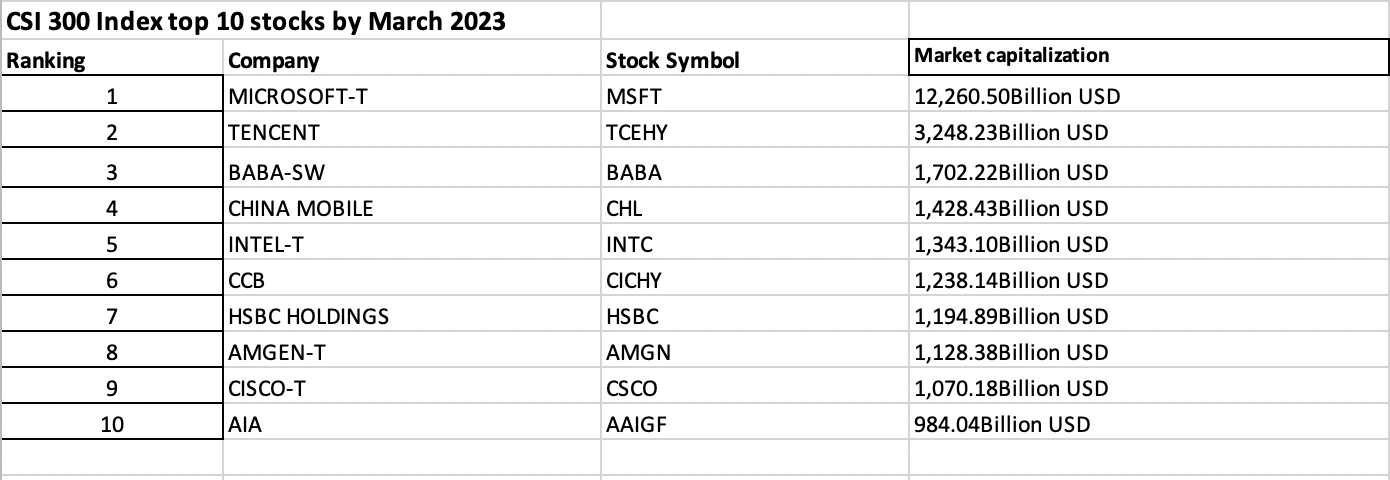
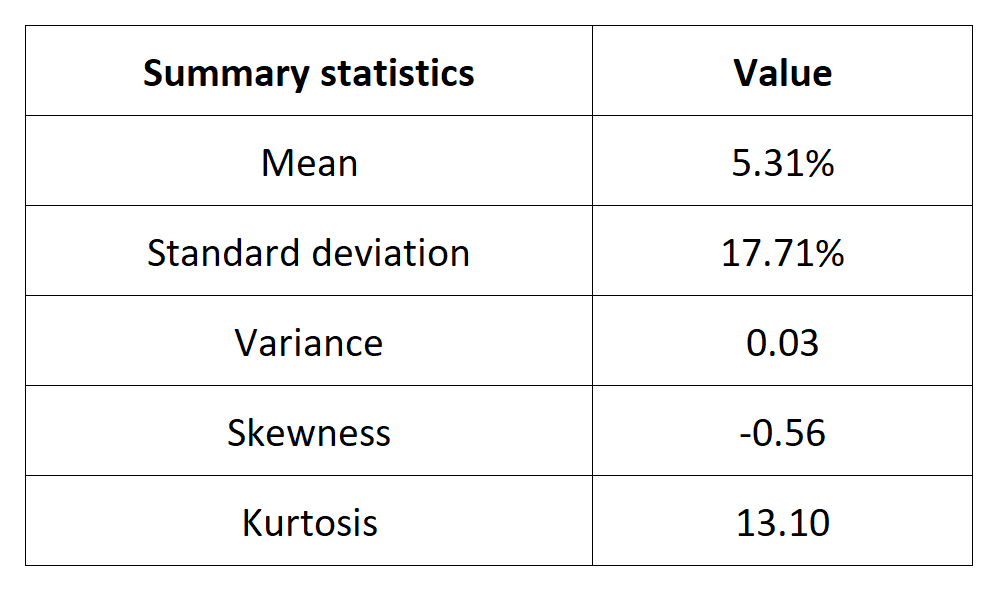
Number of coins
The information on the number of coins in circulation for a given currency is important to compute its market capitalization. Market capitalization is calculated by multiplying the current price of the cryptocurrency by its circulating number of coins (supply). This metric gives a rough estimate of the cryptocurrency’s total value within the market and its relative size compared to other cryptocurrencies. A lower circulating supply often implies a greater level of scarcity and rarity.
For cryptocurrencies (unlike fiat money), the number of coins in circulation is given by a mathematical formula. The number of coins may be limited (like the Bitcoin) or unlimited (like Ethereum and Dogecoin) over time.
Cryptocurrencies with limited supplies, such as Bitcoin’s maximum supply of 21 million coins, can be perceived as more valuable due to their finite nature. Scarcity can contribute to investor interest and potential price appreciation over time. A lower circulating supply might indicate the potential for future adoption and value appreciation, as the limited supply can create scarcity-driven demand, especially if the cryptocurrency gains more utility and usage.
Bitcoin’s blockchain also relies on a key equation to steadily allow new BTC to be introduced. The equation below gives the total supply of bitcoins:
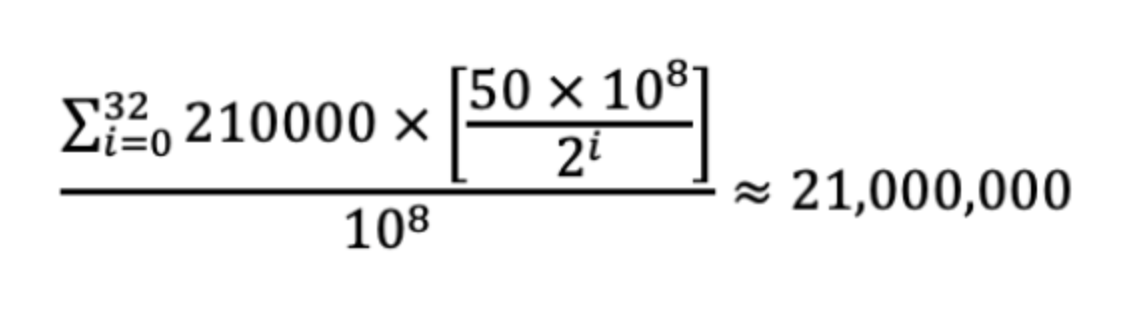
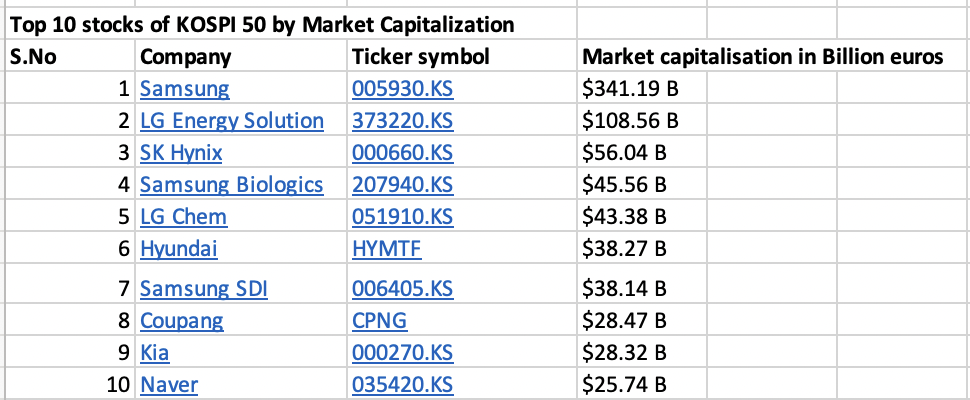
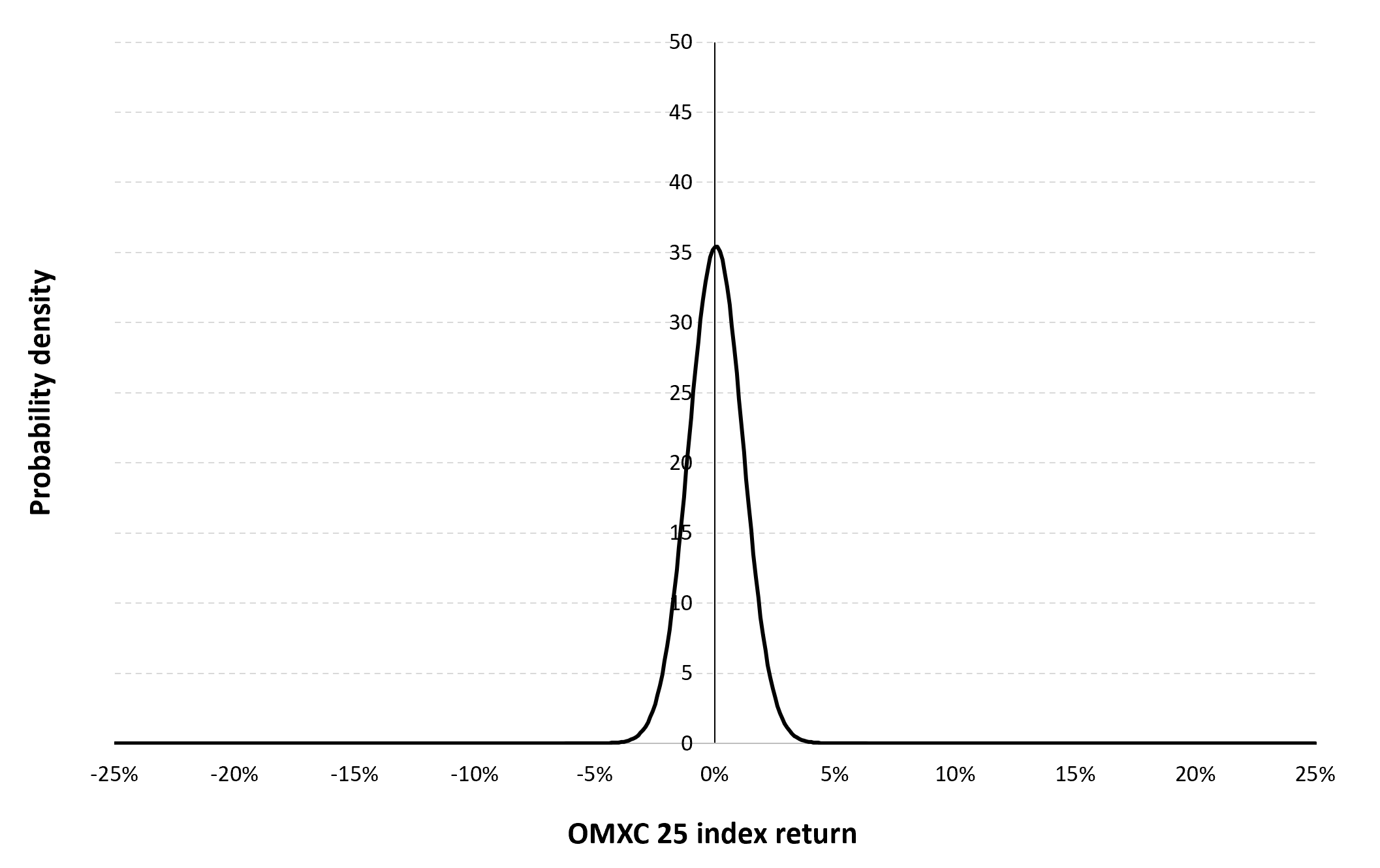
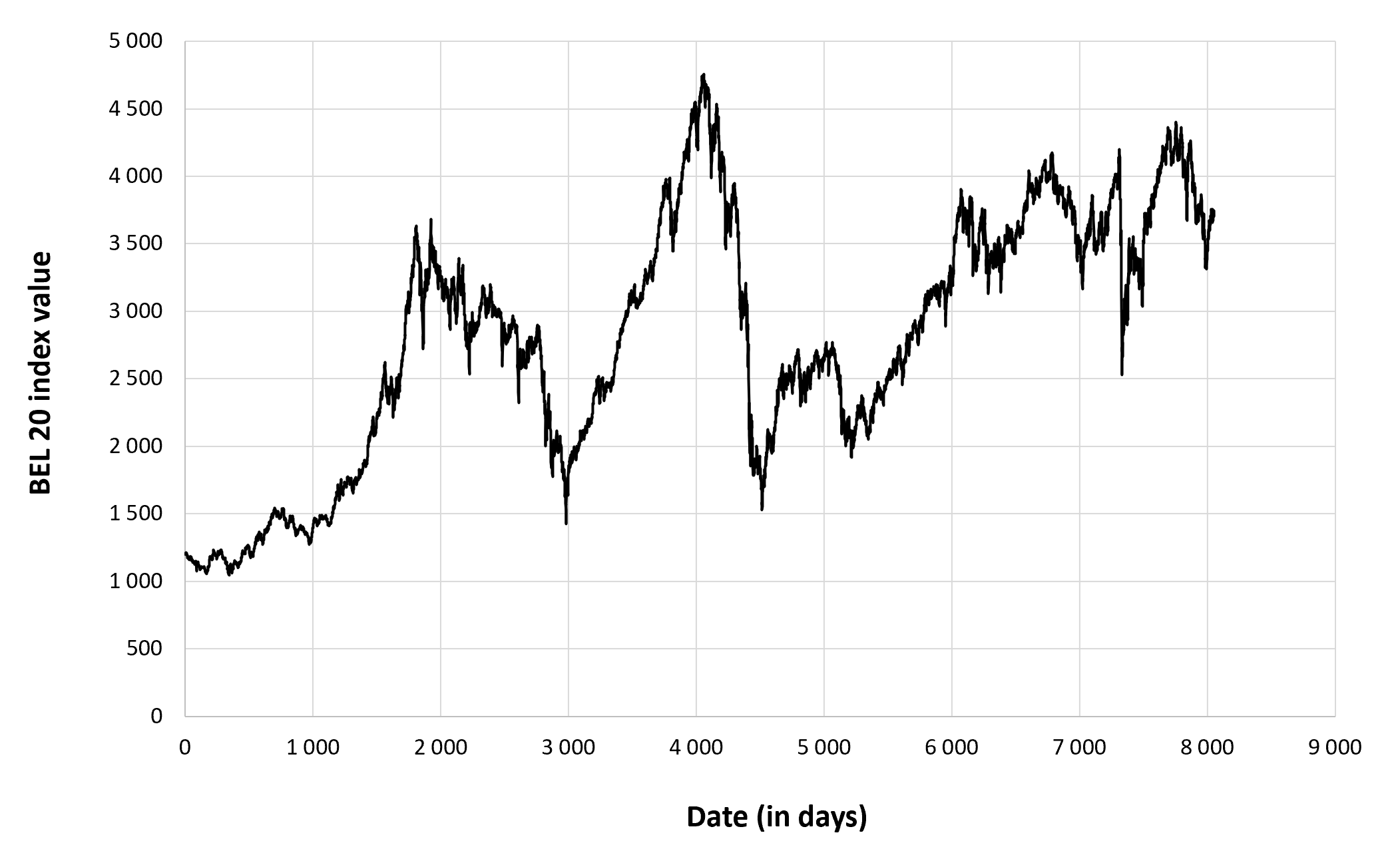
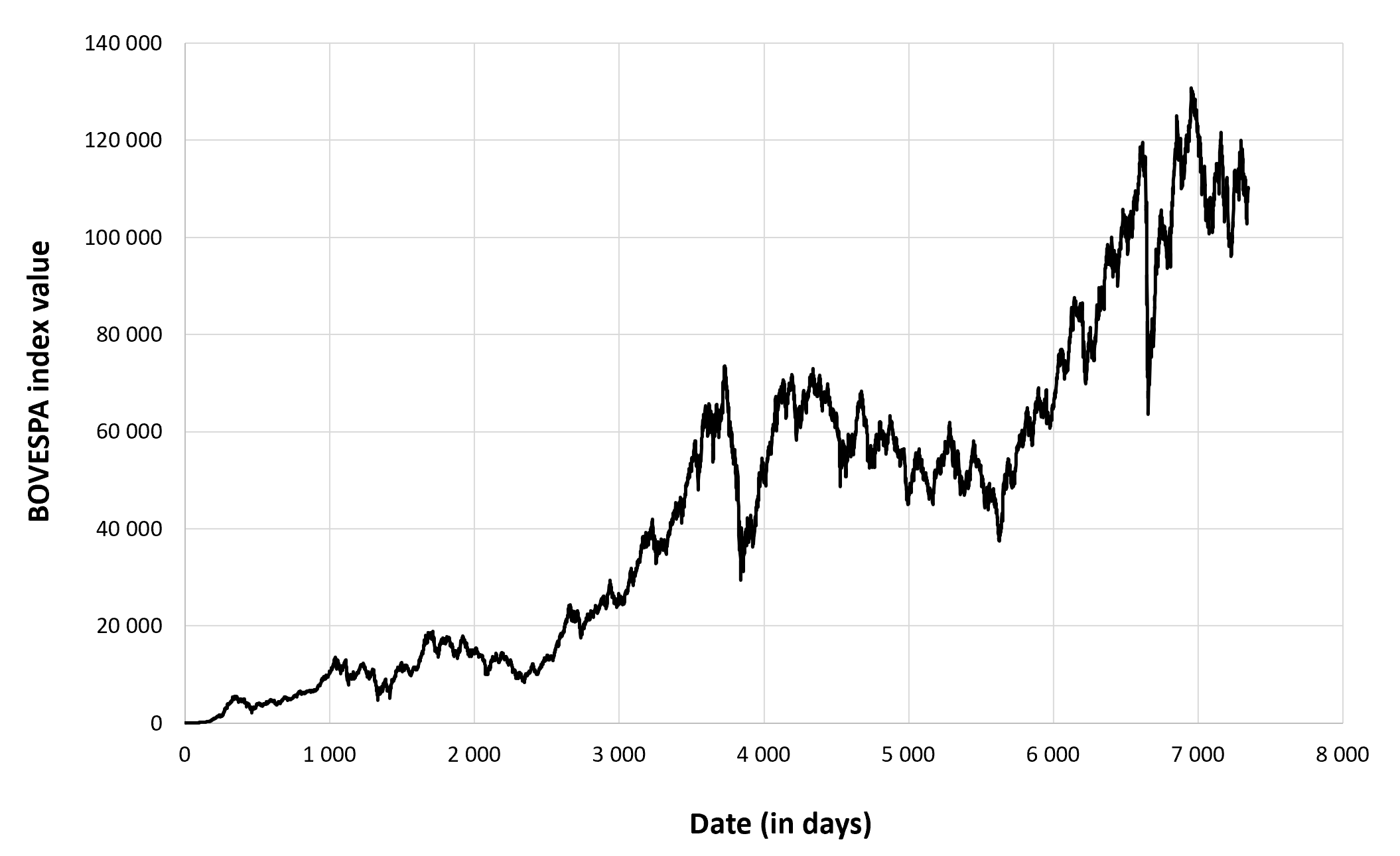
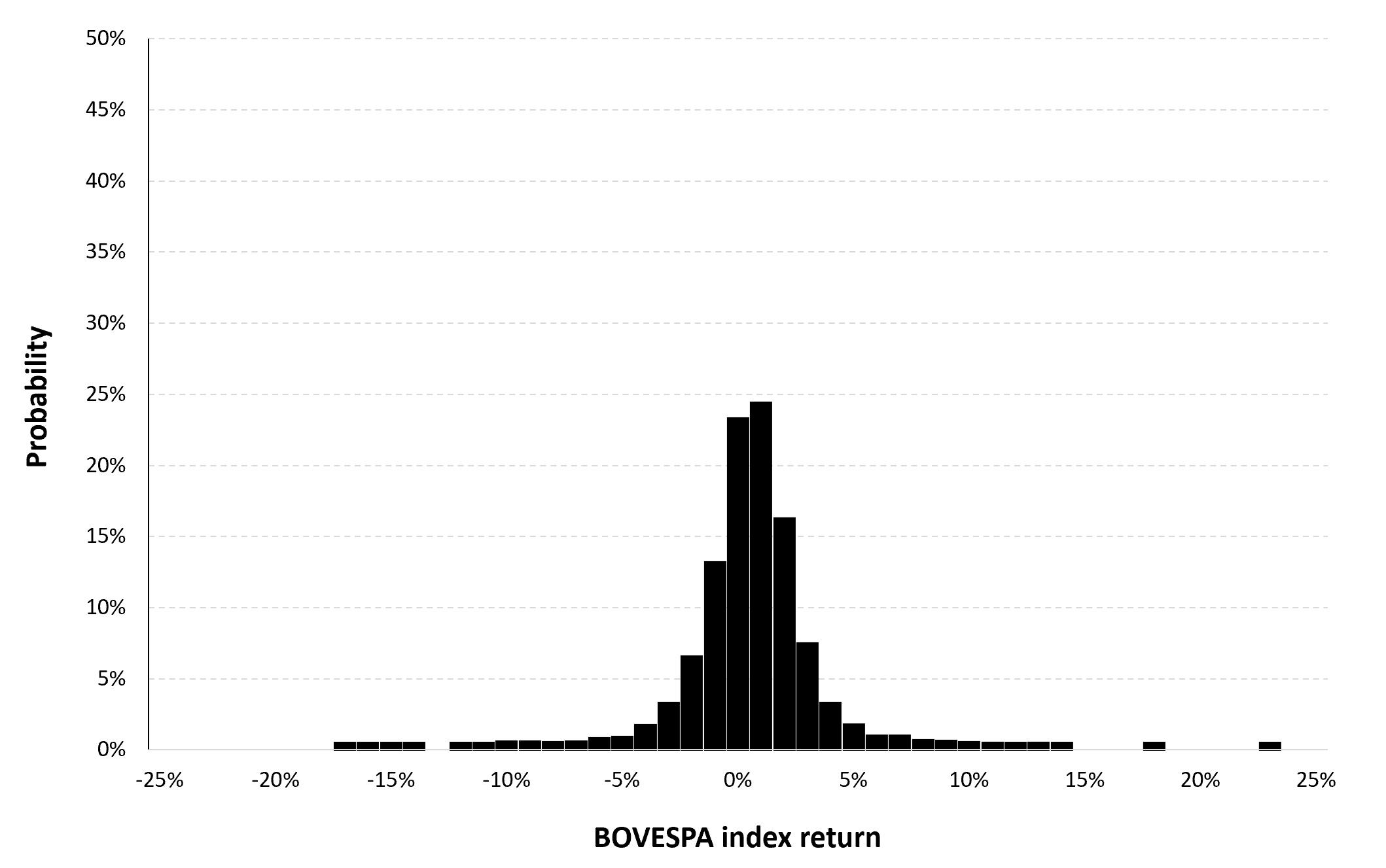
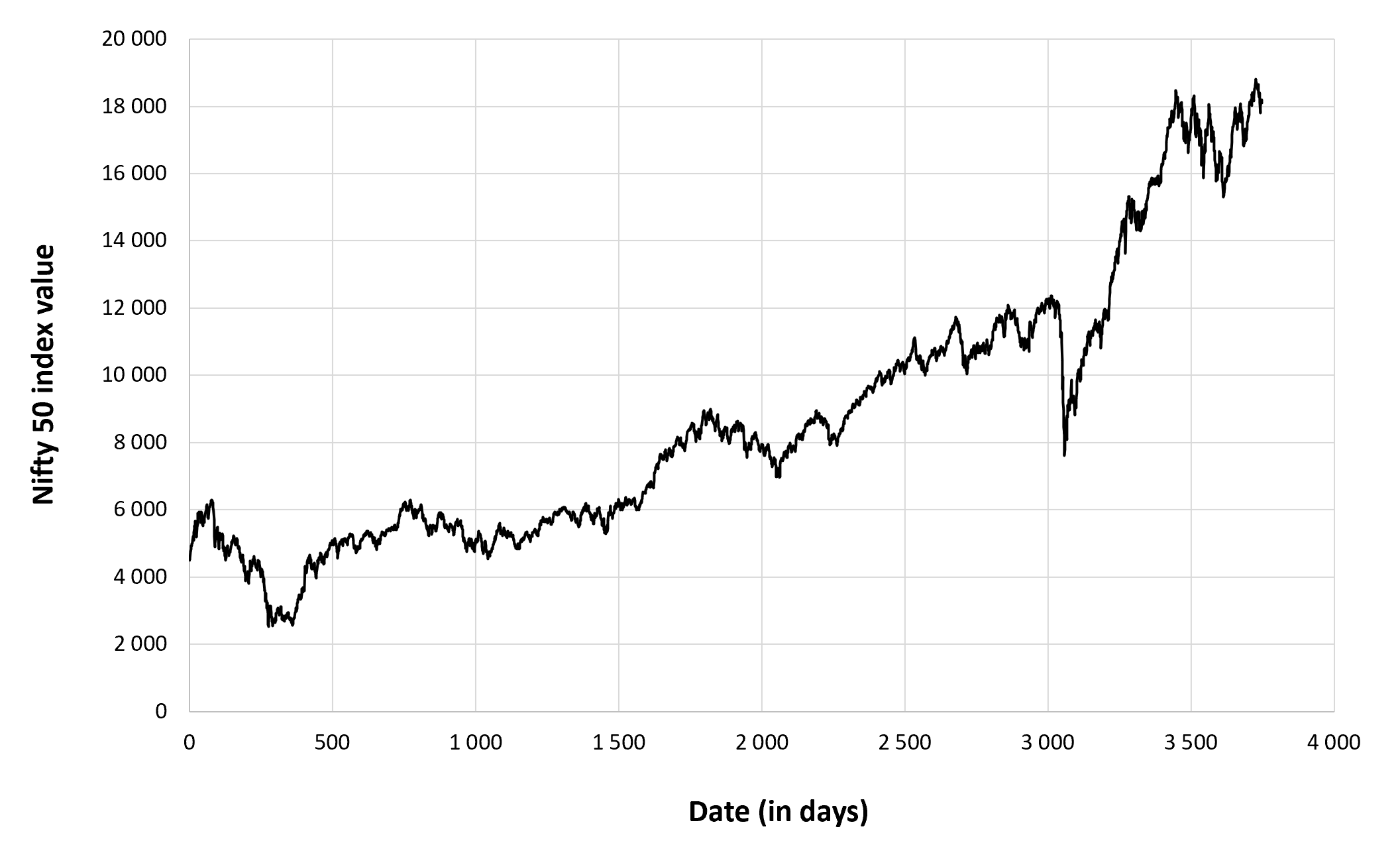
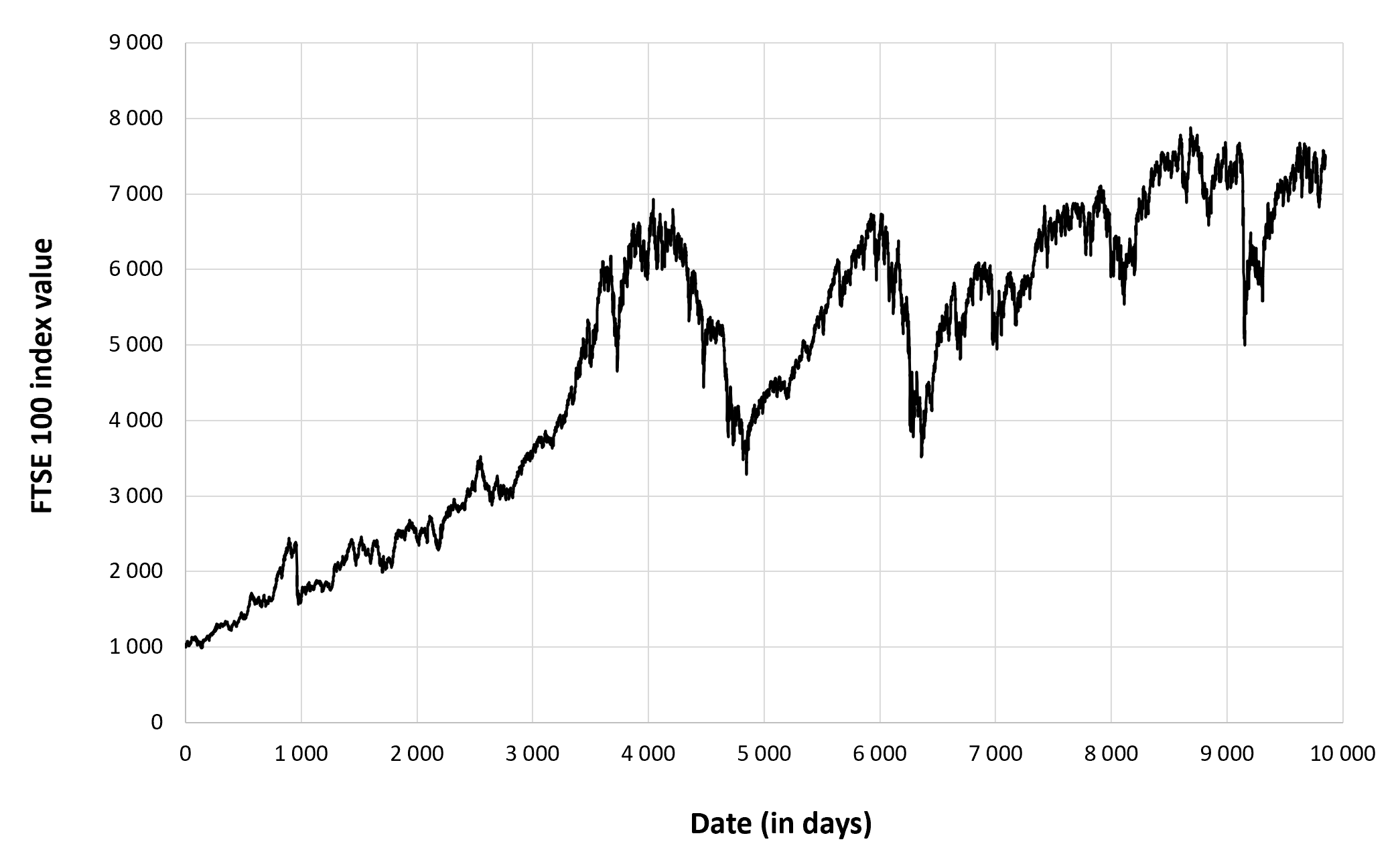
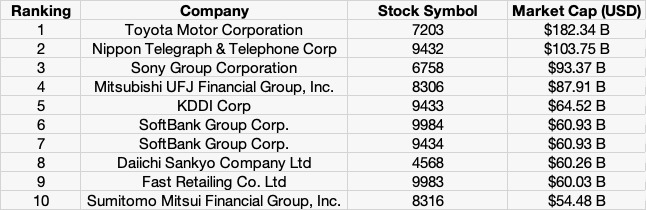
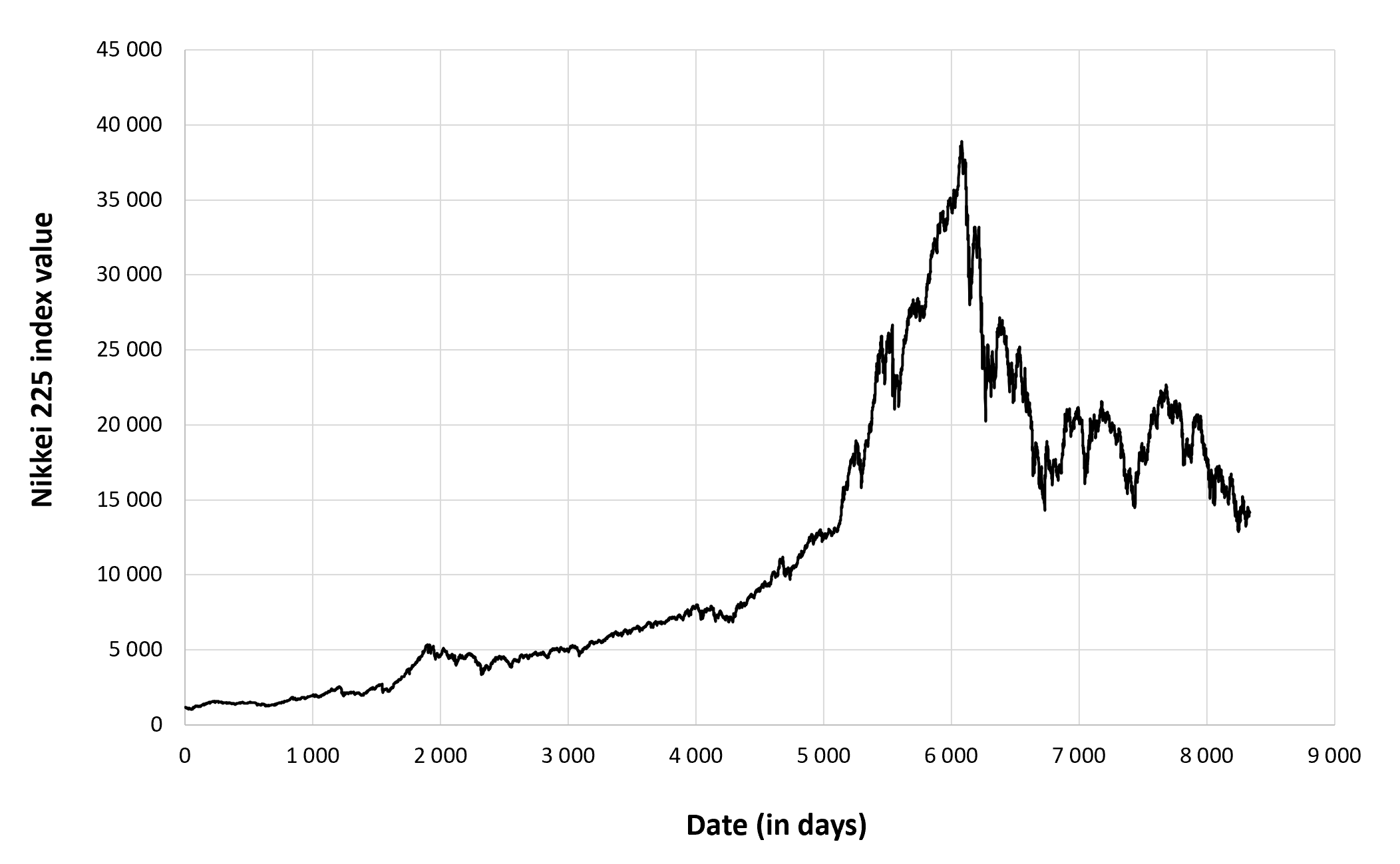
Figure 1 below represents the evolution of the supply of Bitcoins.
Figure 1. Evolution of the supply of Bitcoins
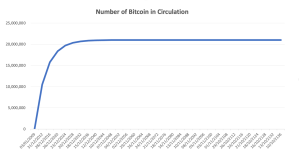
Source: computation by the author.
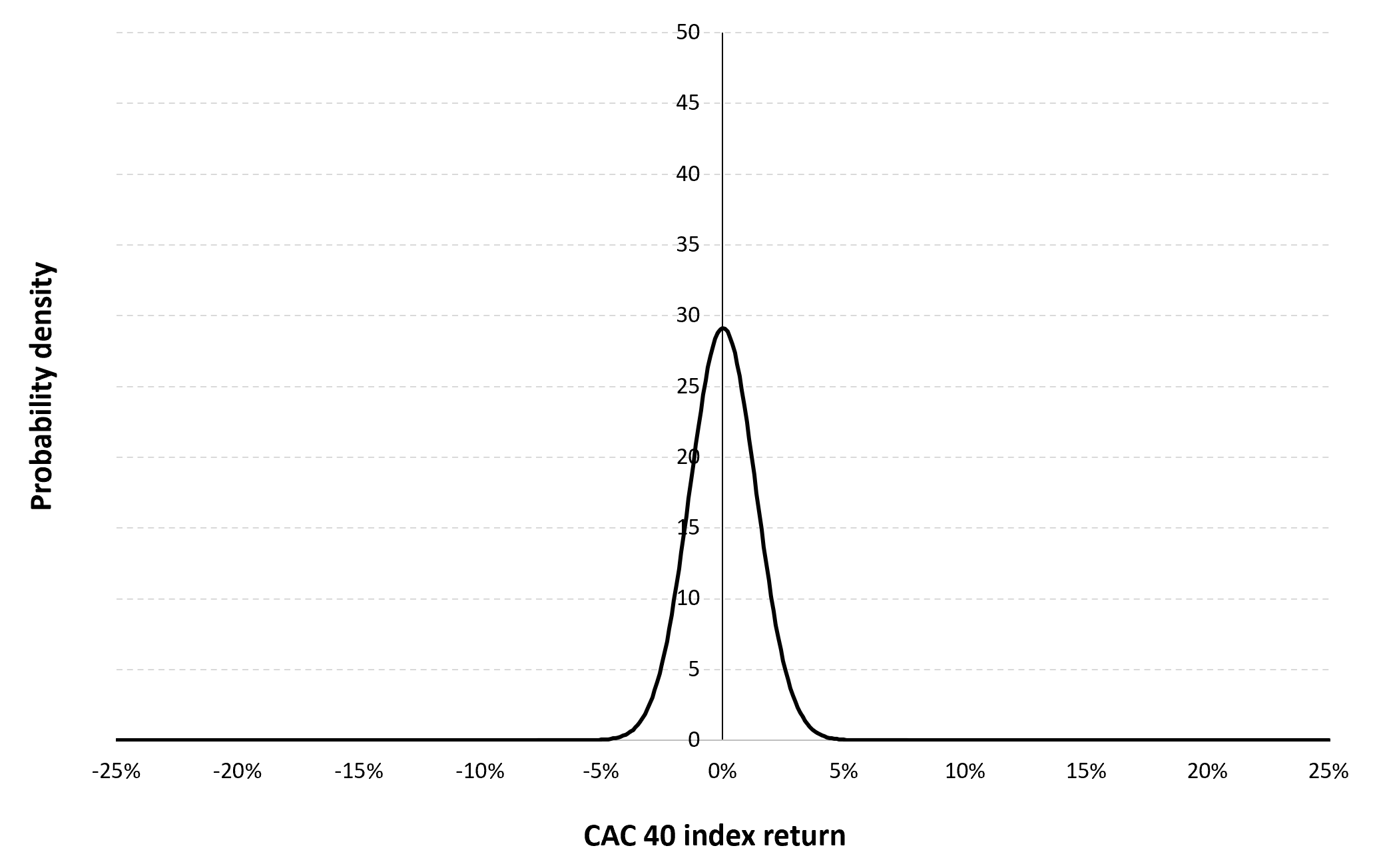
Market price of a coin
The market price of a cryptocurrency in the market holds crucial insights into how well the cryptocurrency is faring. Although not the sole factor, the market price significantly contributes to evaluating the cryptocurrency’s performance and its prospects. The market price of a cryptocurrency is a dynamic and intricate element that reflects a multitude of factors, both intrinsic and extrinsic. The gradual rise in market value over time indicates a willingness among investors and traders to offer higher prices for the cryptocurrency. This signifies a rising interest and strong belief in the project’s potential for the future. The market price reflects the collective sentiment of investors and traders. Comparing the market price of a cryptocurrency to other similar cryptocurrencies or benchmark assets like Bitcoin can provide insights into its relative strength and performance within the market. A rising market price can indicate increasing adoption of the cryptocurrency for various use cases. Successful projects tend to attract more users and real-world applications, which can drive up the price.
The value of cryptocurrencies in the market is influenced by a variety of elements, with each factor contributing uniquely to their pricing. One of the most significant influences is market sentiment and investor psychology. These factors can cause prices to shift based on positive news, regulatory changes, or reactive selling due to fear. Furthermore, the real-world implementation and usage of a cryptocurrency are crucial for its prosperity. Concrete use cases such as Decentralized Finance (DeFi), Non-Fungible Tokens (NFTs), and international transactions play a vital role in creating demand and propelling price appreciation. Meanwhile, adherence to basic economic principles is evident in the supply-demand dynamics, where scarcity due to limited issuance, halving events, and token burns interact with the balance between supply and demand.
With the number of coins in circulation, the information on the price of coins for a given currency is also important to compute its market capitalization.
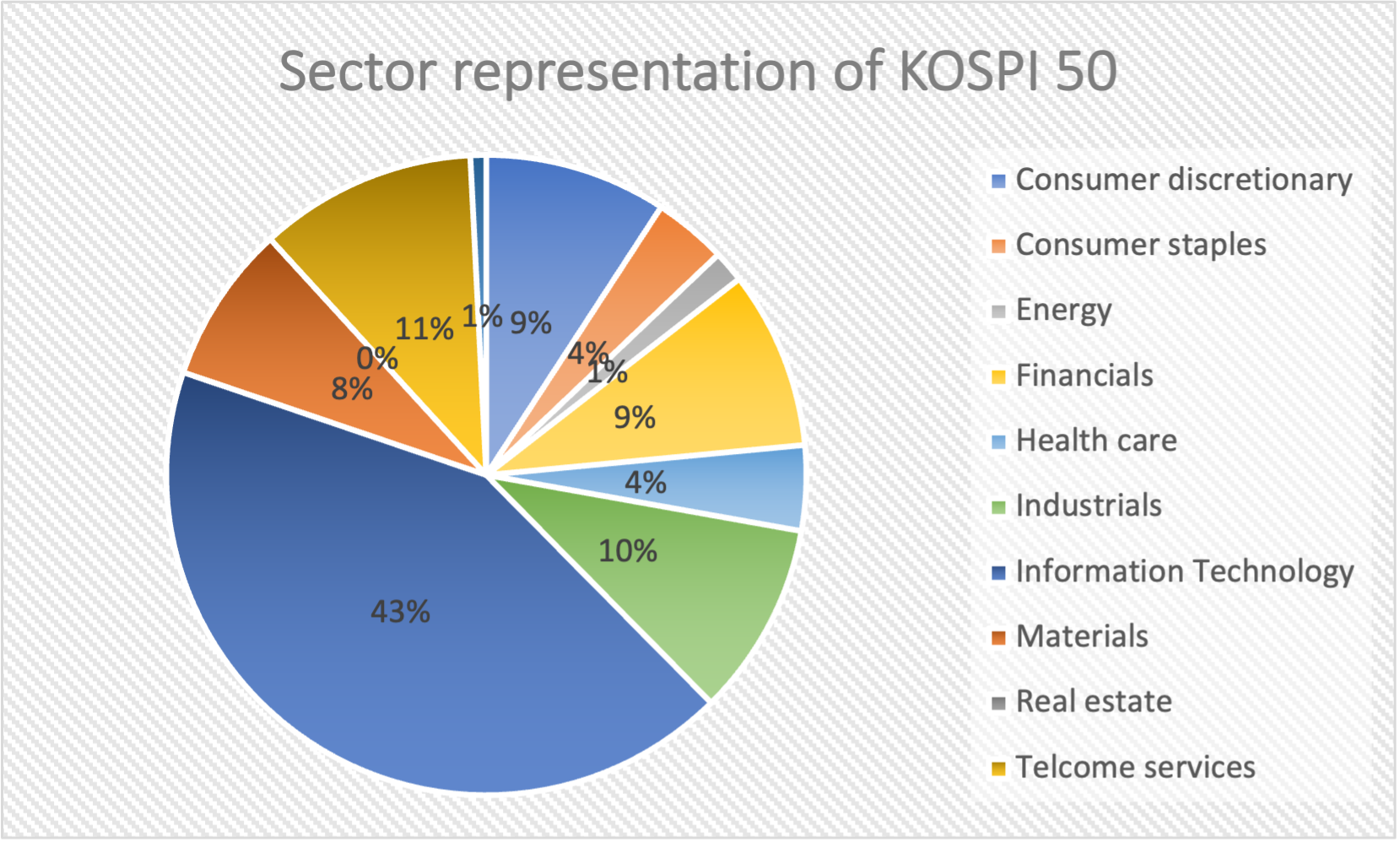
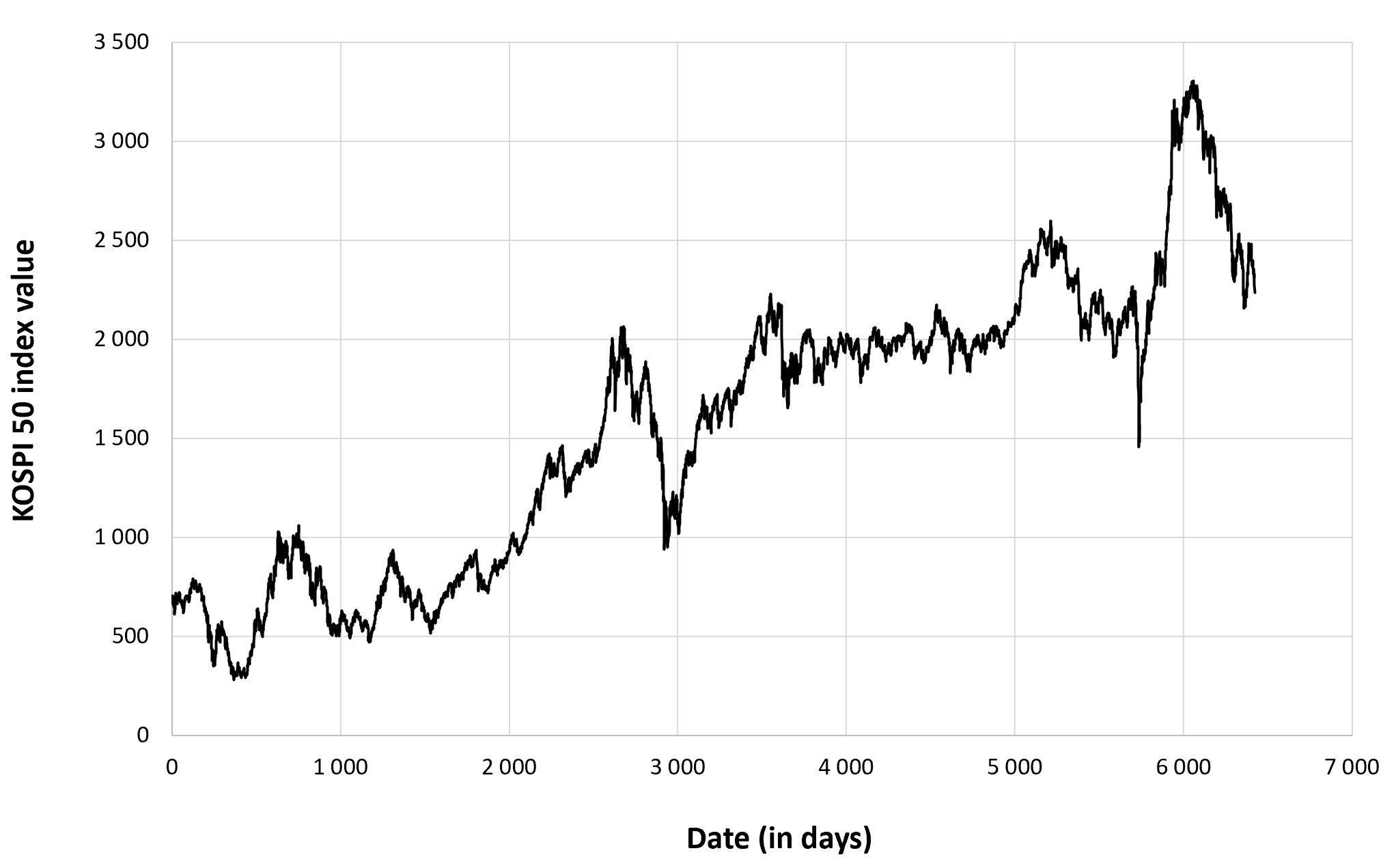
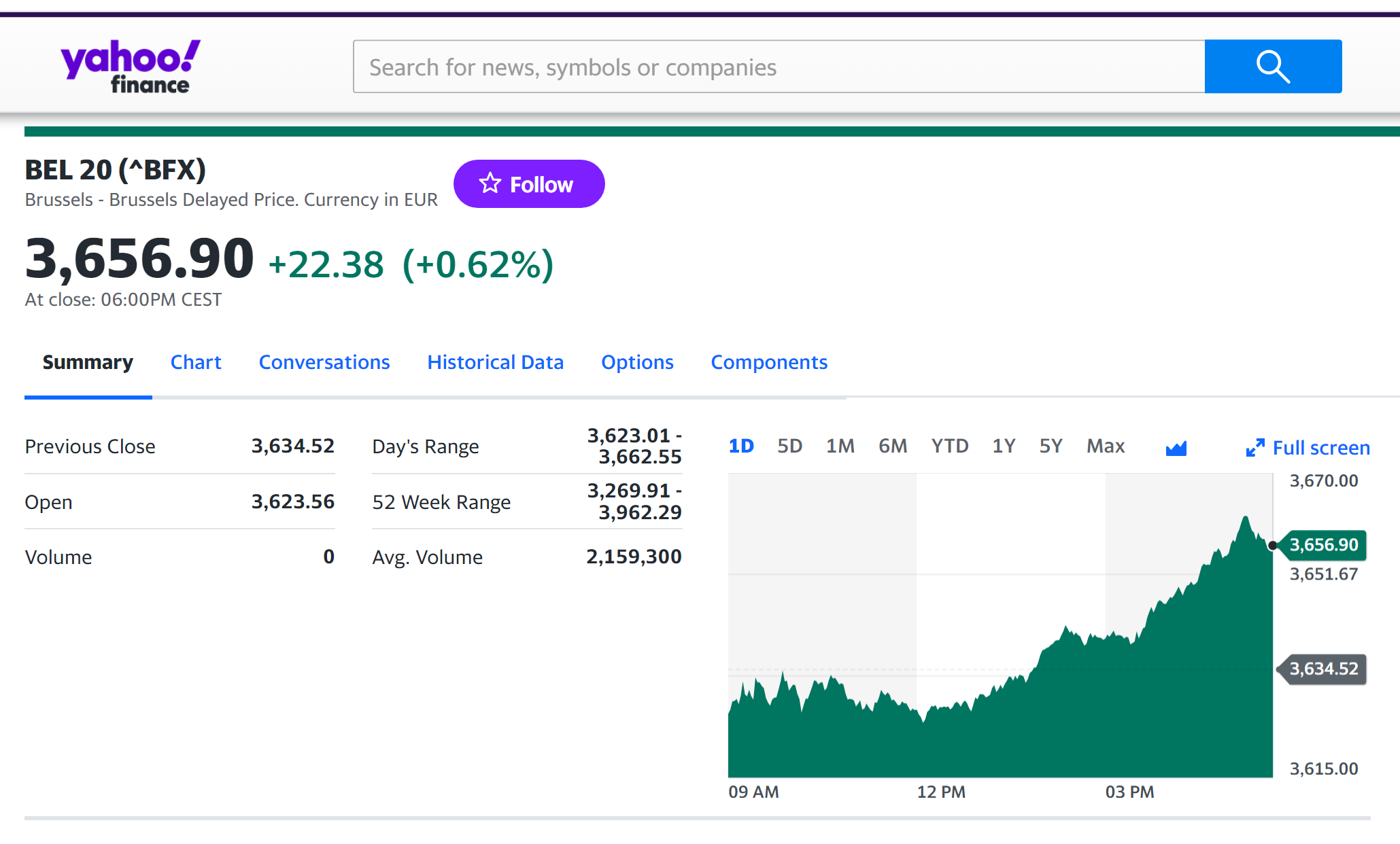
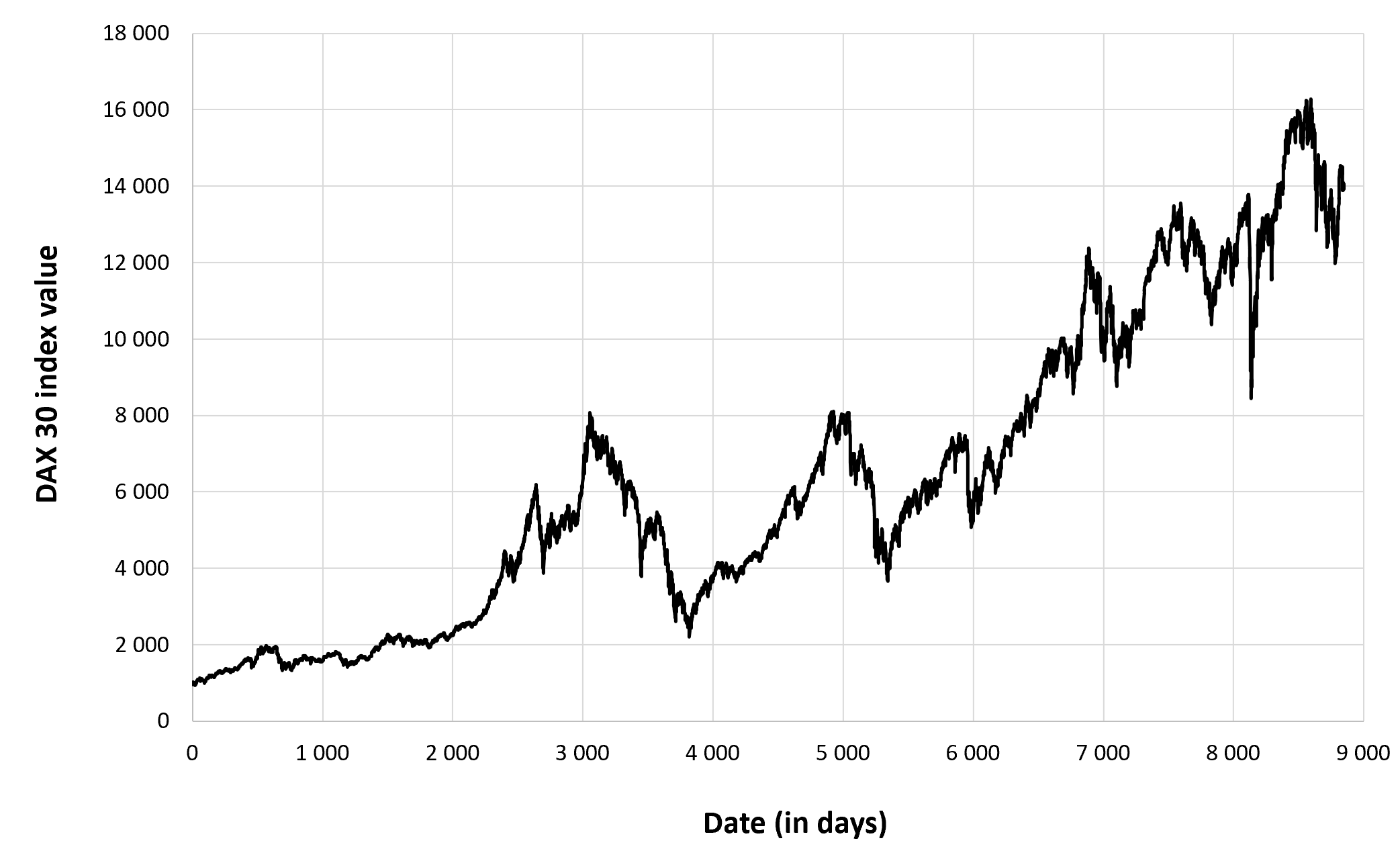
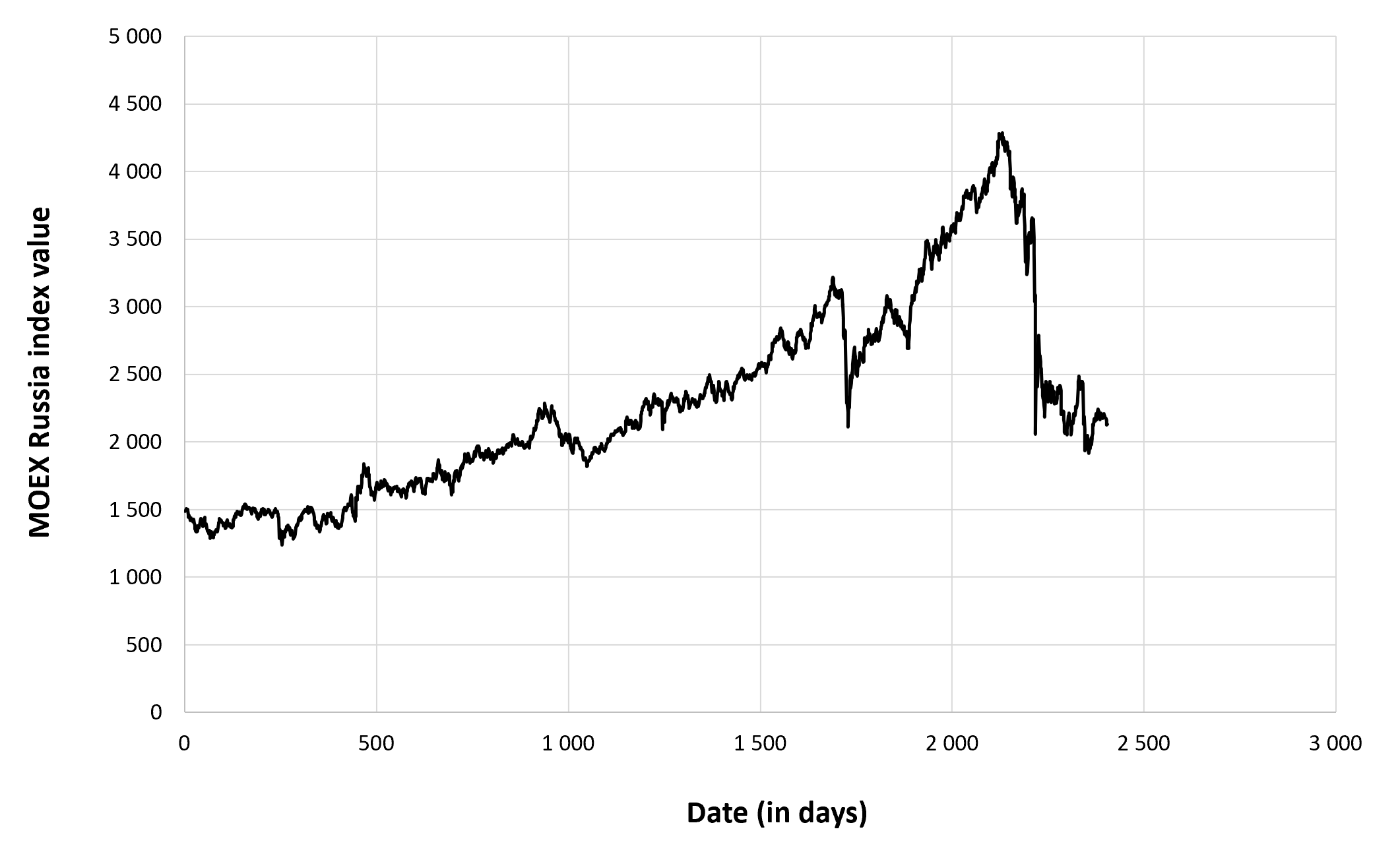
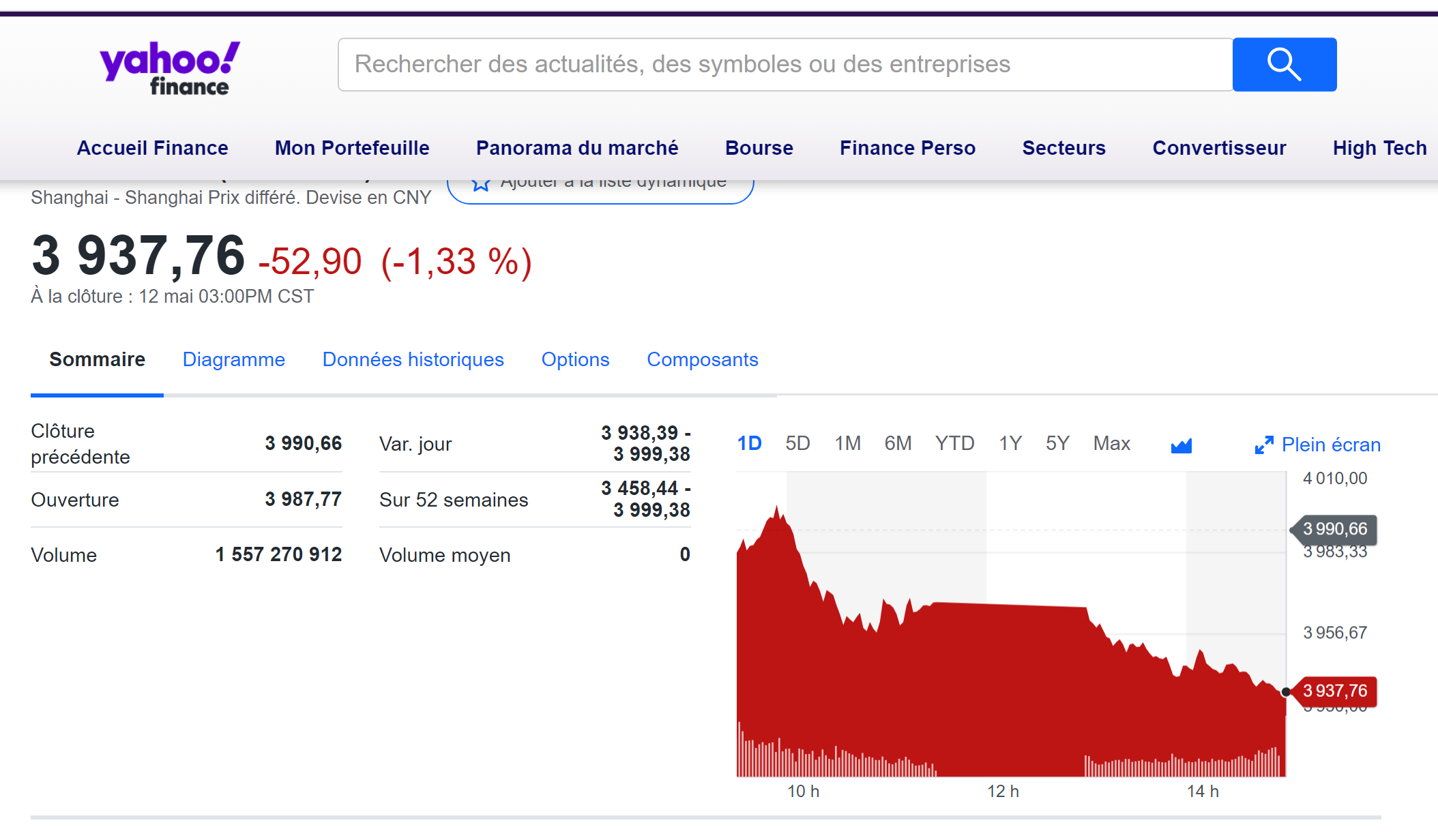
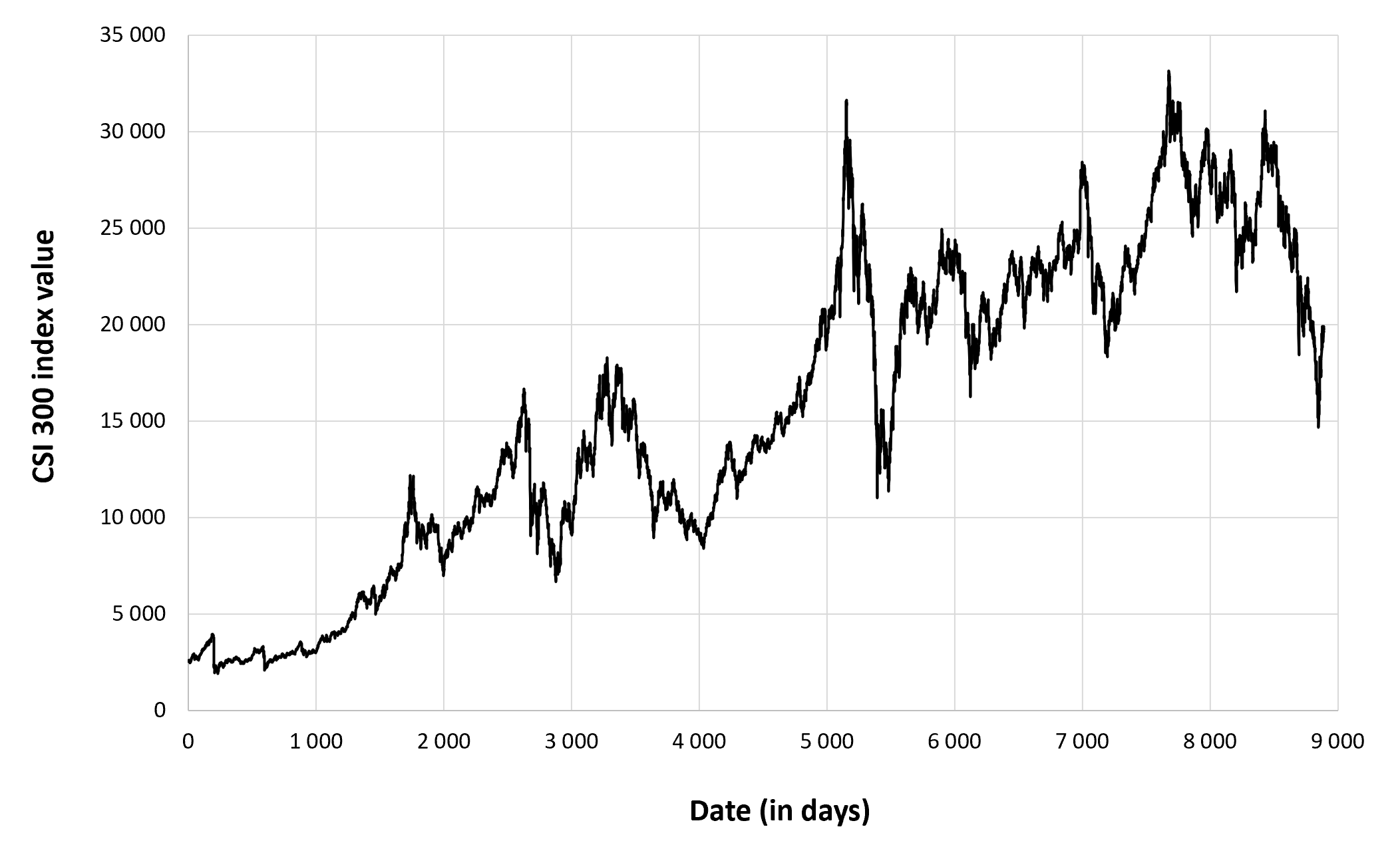
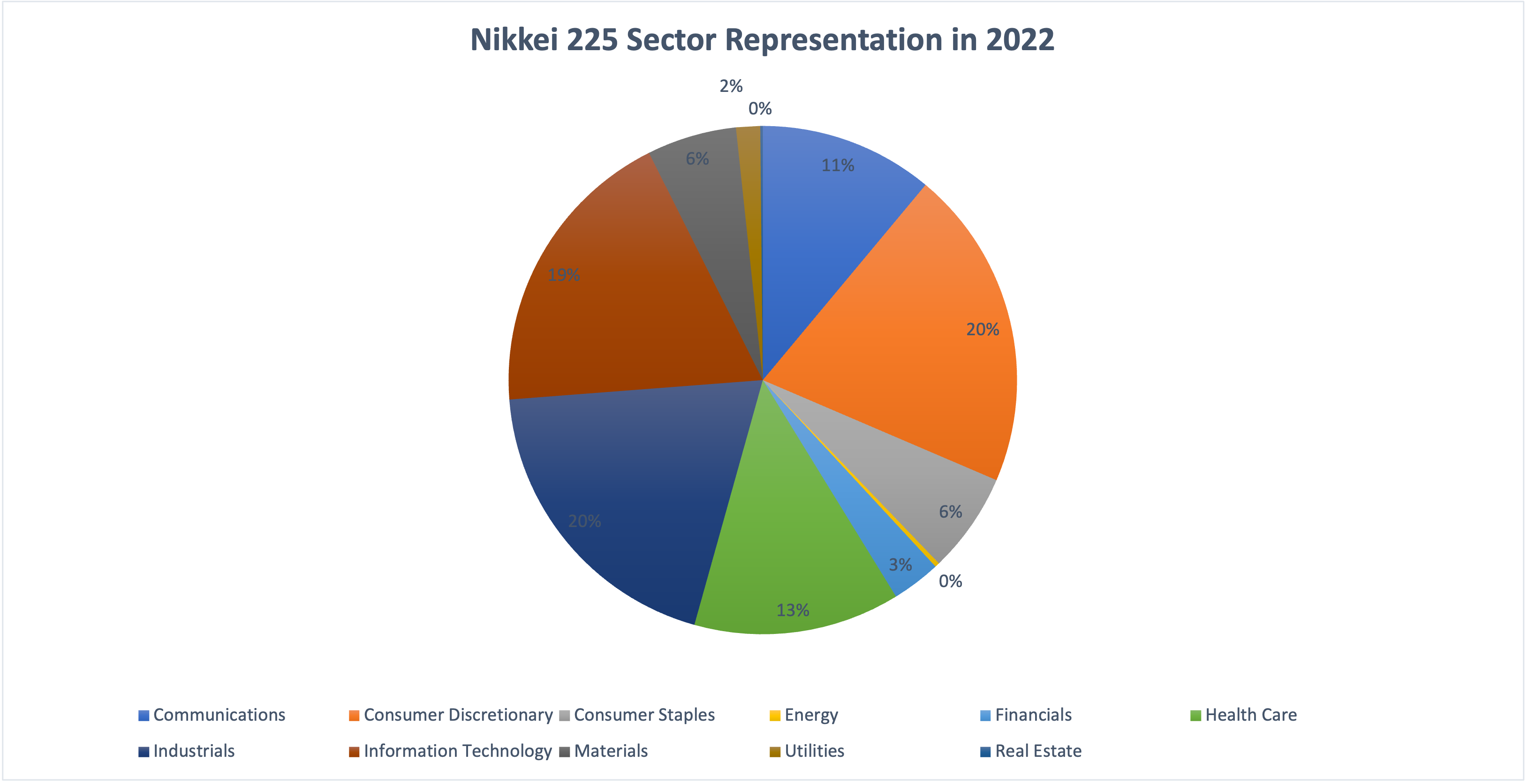
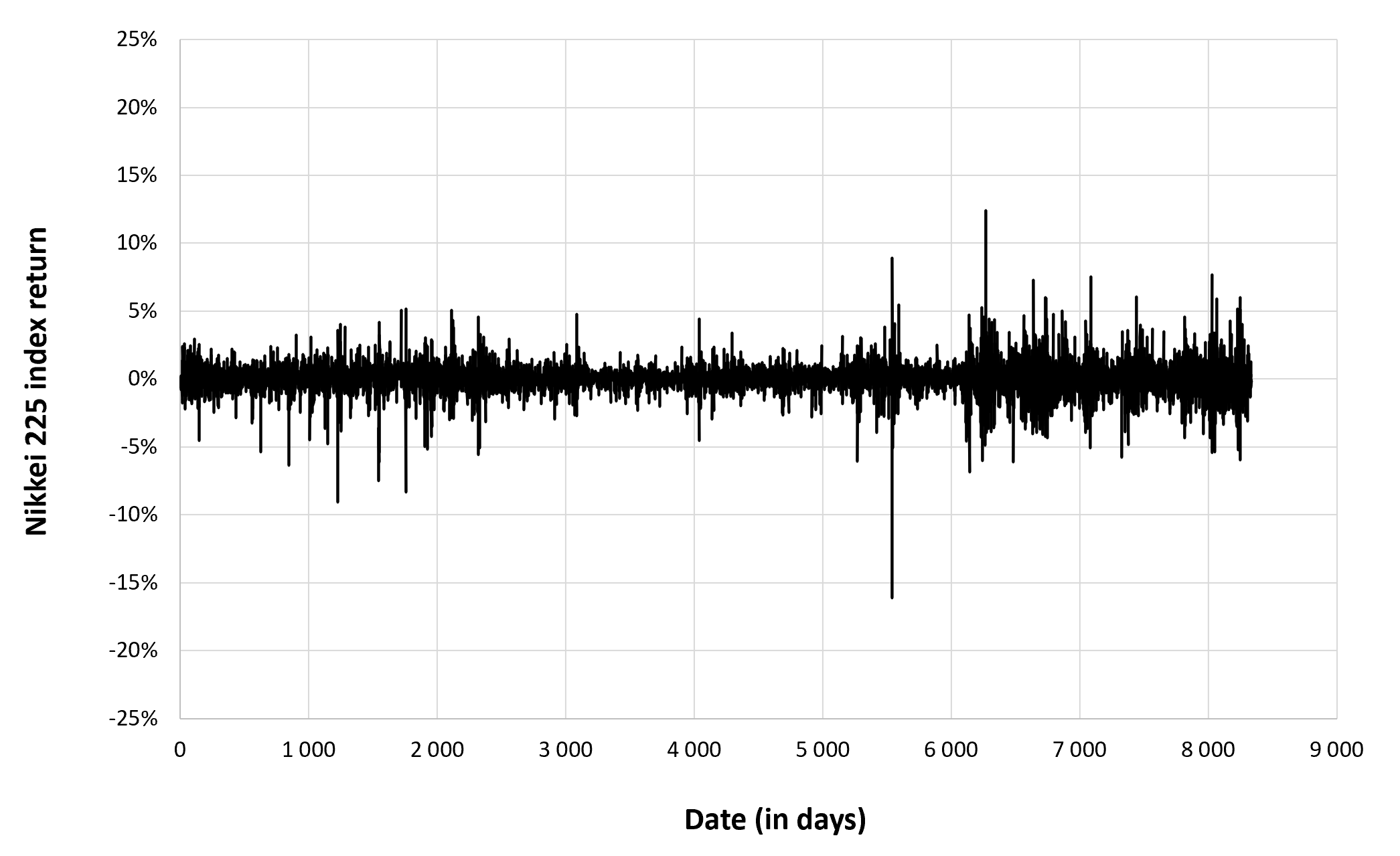
Figure 2 below represents the evolution of the price of Bitcoin in US dollar over the period October 2014 – August 2023. The price corresponds to the “closing” price (observed at 10:00 PM CET at the end of the month).
Figure 2. Evolution of the Bitcoin price
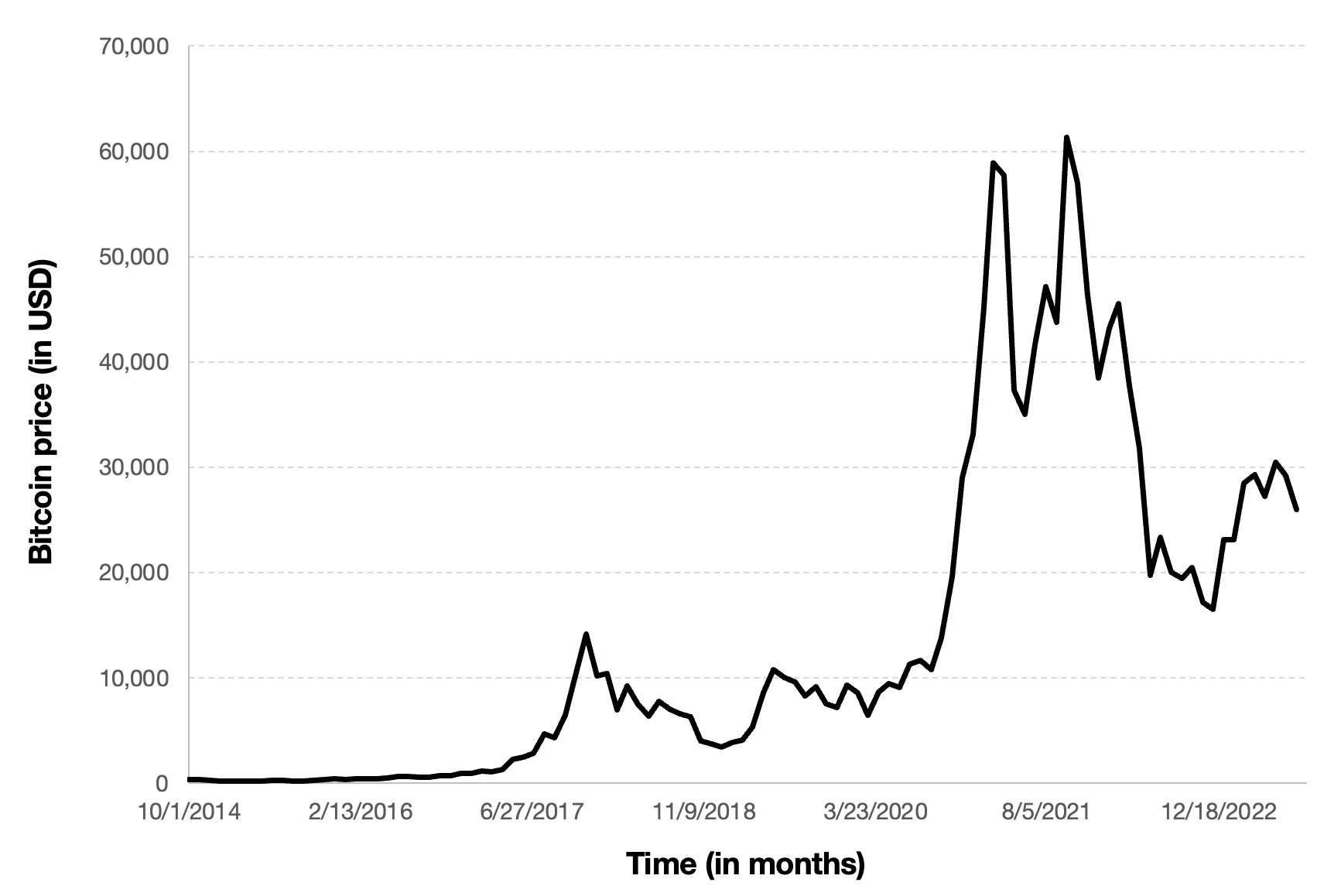
Source: computation by the author (data source: Yahoo! Finance).
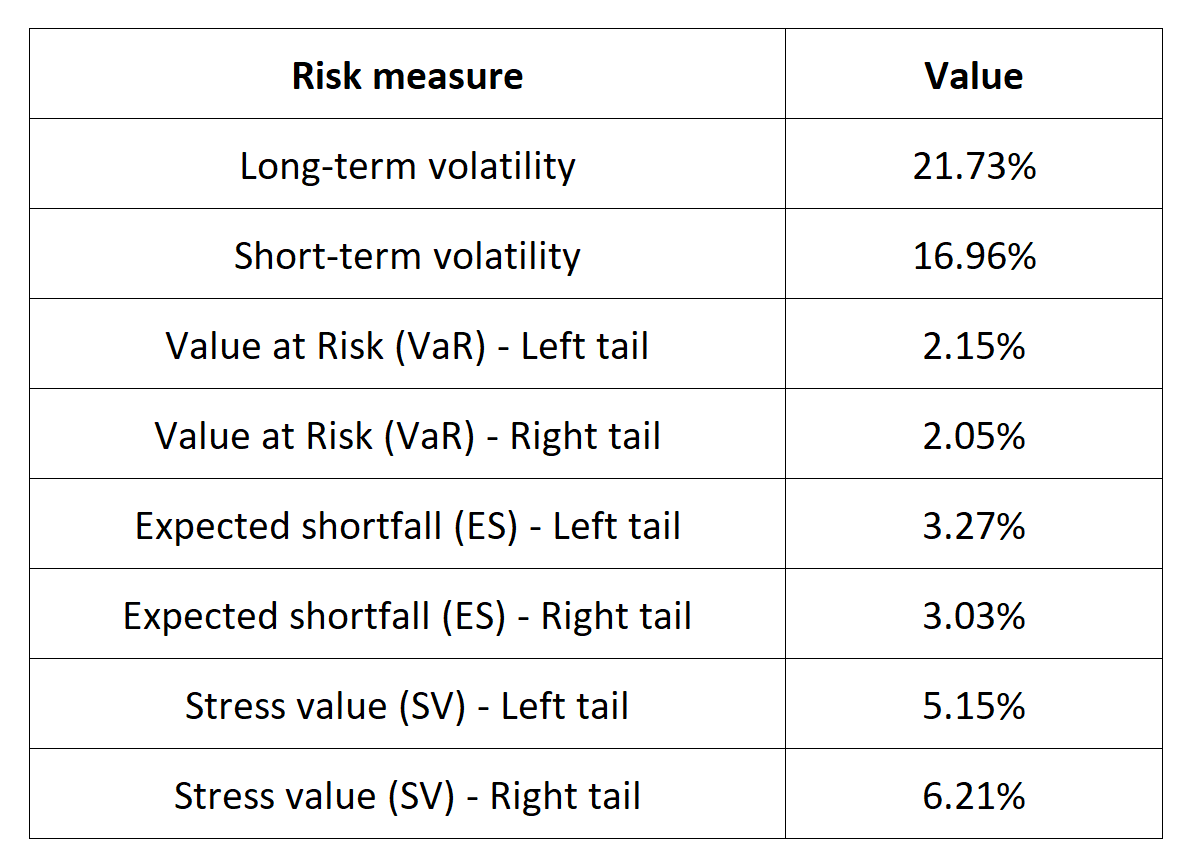
Trading volume
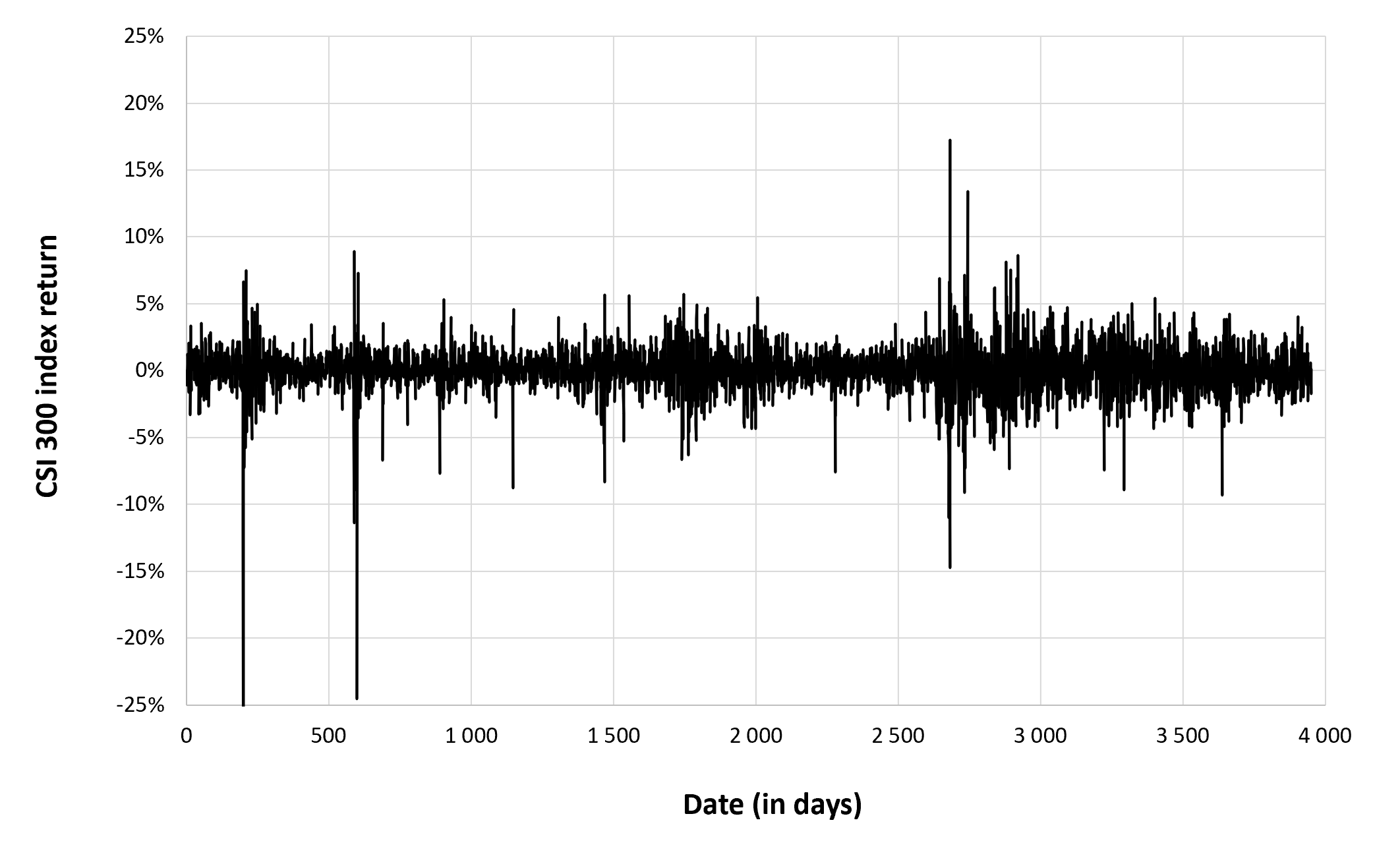
Trading volume is crucial when assessing the health, reliability, and potential price movements of a cryptocurrency. Trading volume refers to the total amount of a cryptocurrency that is bought and sold within a specific time frame, typically measured in units of the cryptocurrency (e.g., BTC) or in terms of its equivalent value in another currency (e.g., USD).
Trading volume directly mirrors market liquidity, with higher volumes indicative of more liquid markets. This liquidity safeguards against drastic price fluctuations when trading, contrasting with low-volume scenarios that can breed volatility, where even a single substantial trade may disproportionately shift prices. Price alterations are most reliable and meaningful when accompanied by substantial trading volume. Price movements upheld by heightened volume often hold greater validity, potentially pointing to more pronounced market sentiment. When price surges parallel rising trading volume, it suggests a sustainable upward trajectory. Conversely, low trading volume amid rising prices may hint at a forthcoming correction or reversal. Scrutinizing the correlation between price oscillations and trading volume can uncover potential divergences. For instance, ascending prices coupled with dwindling trading volume may suggest a weakening trend.
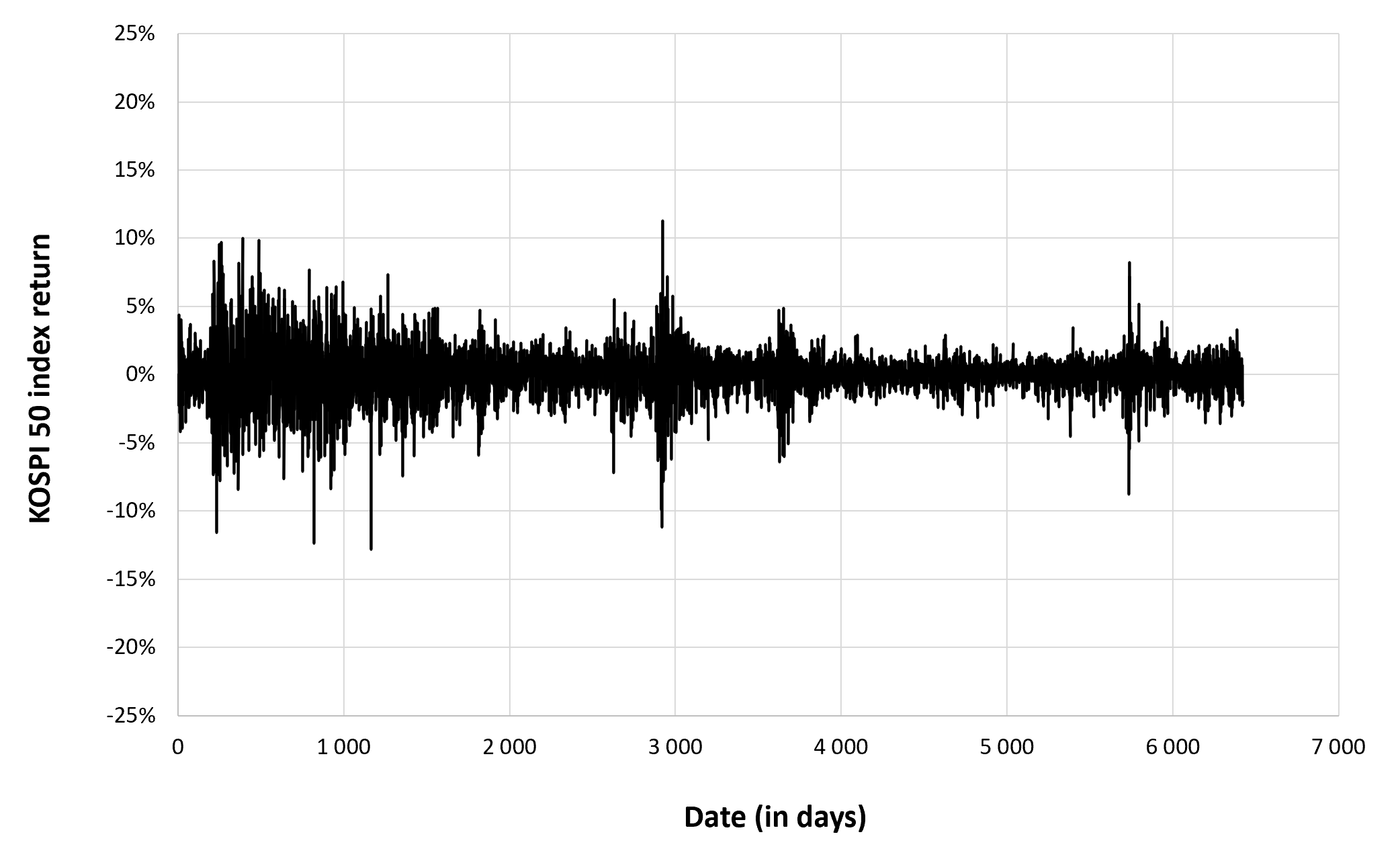
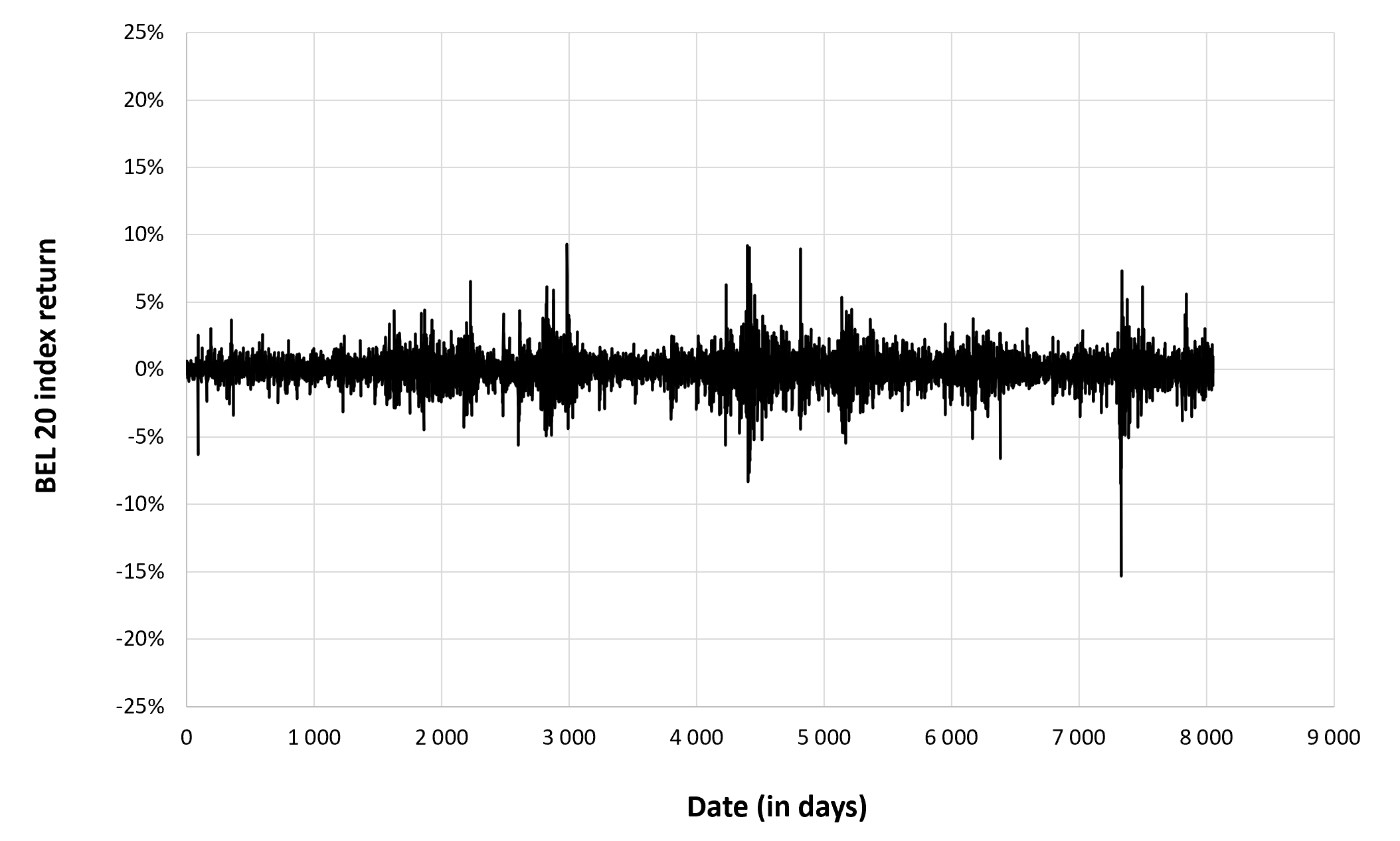
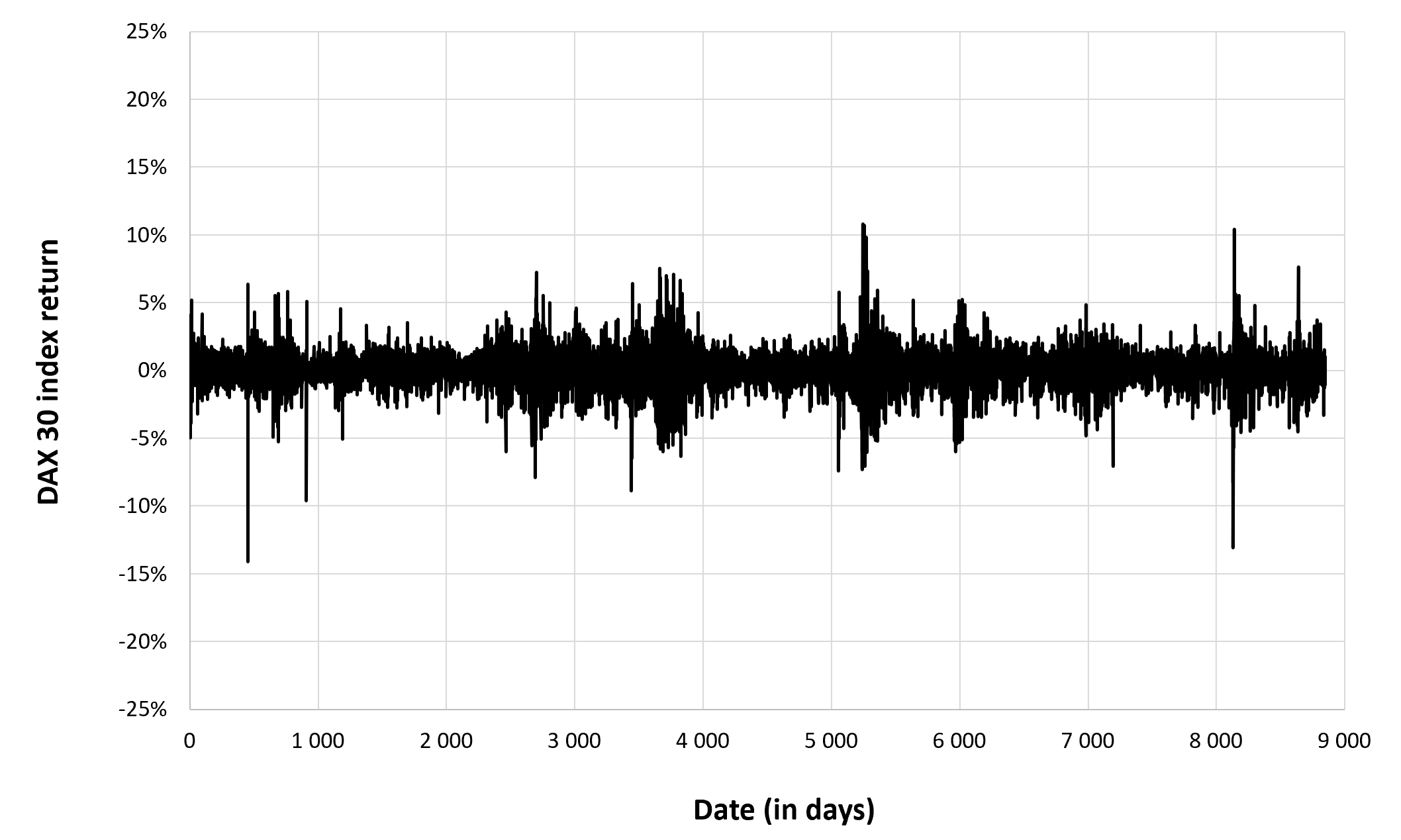
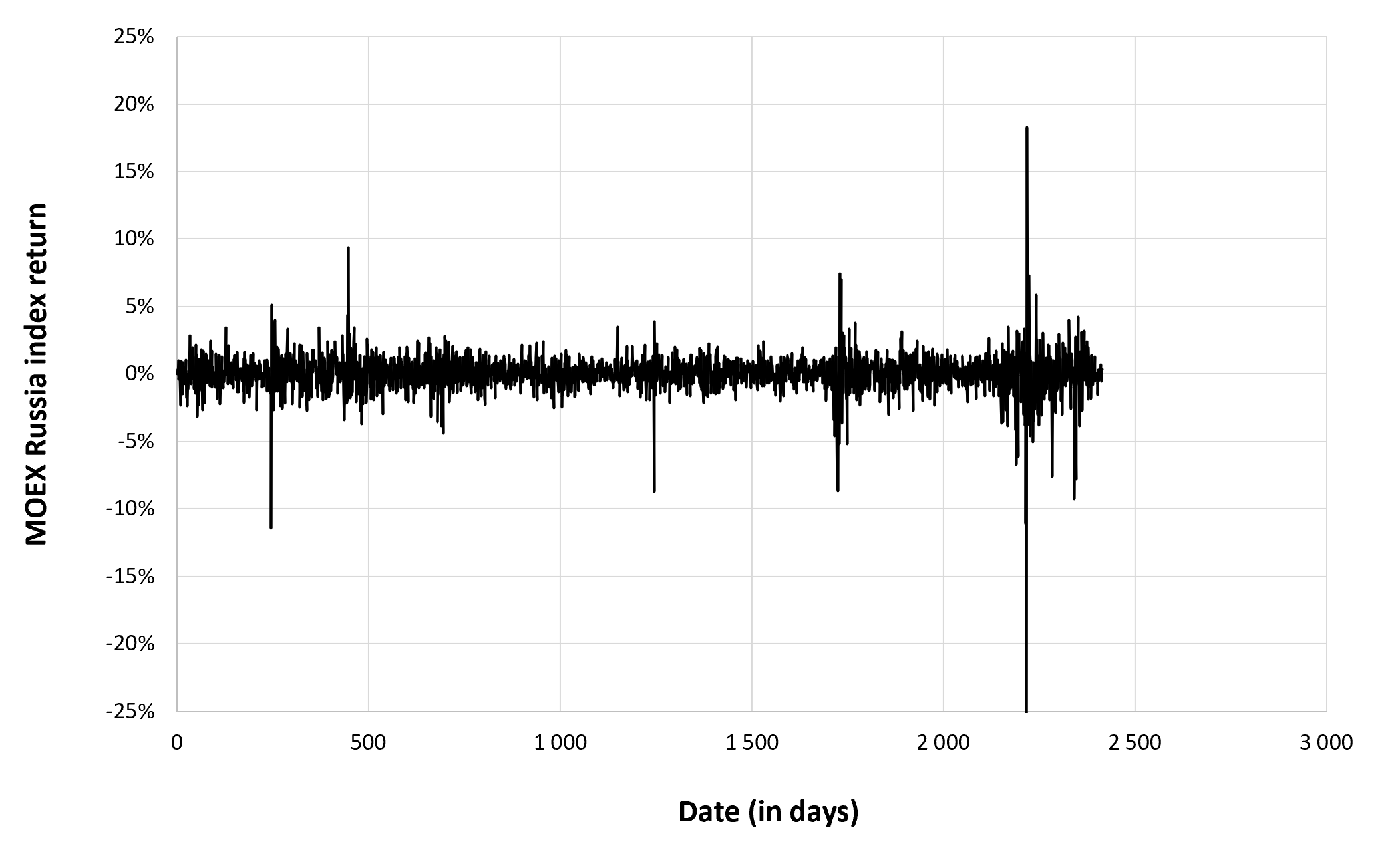
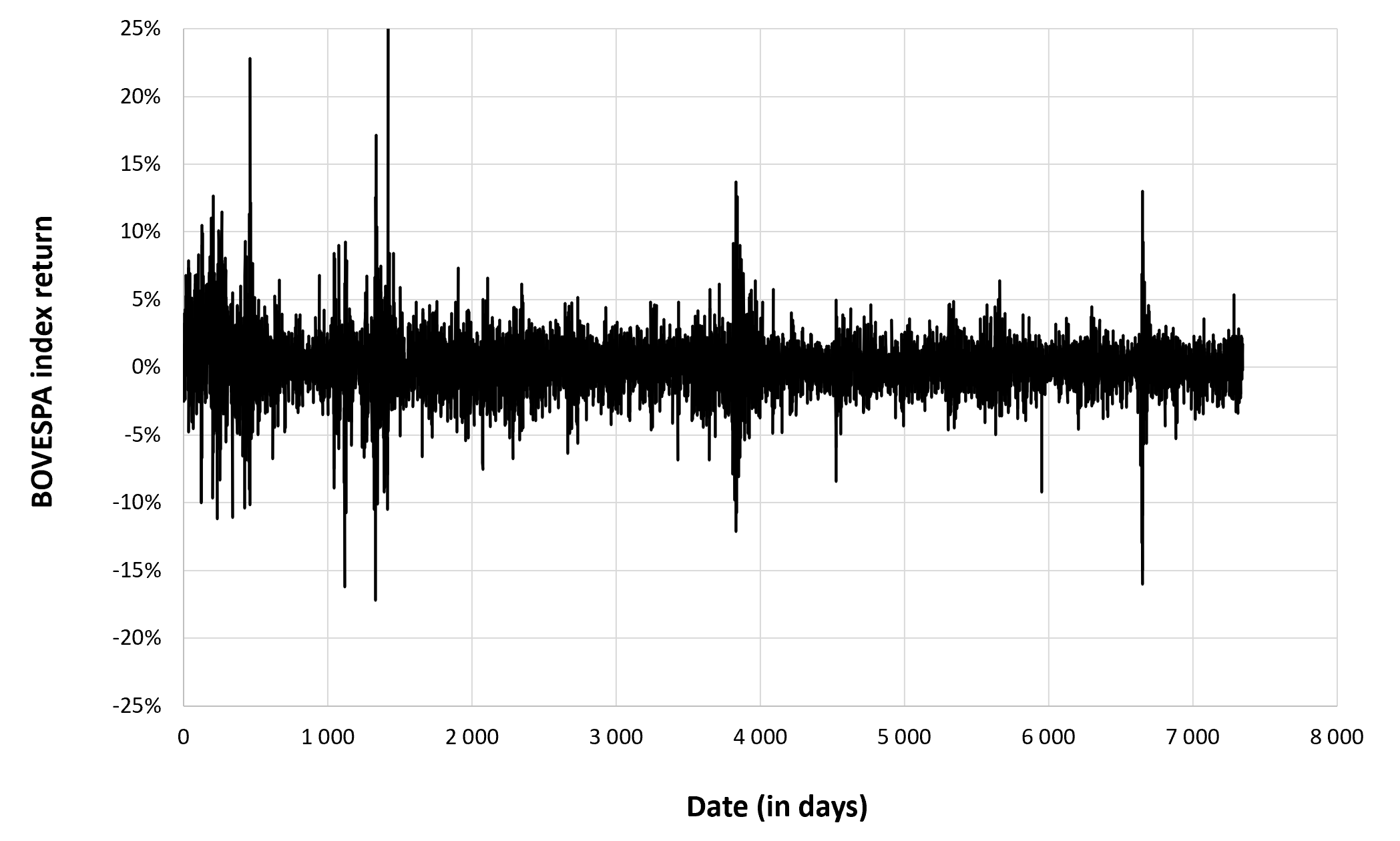
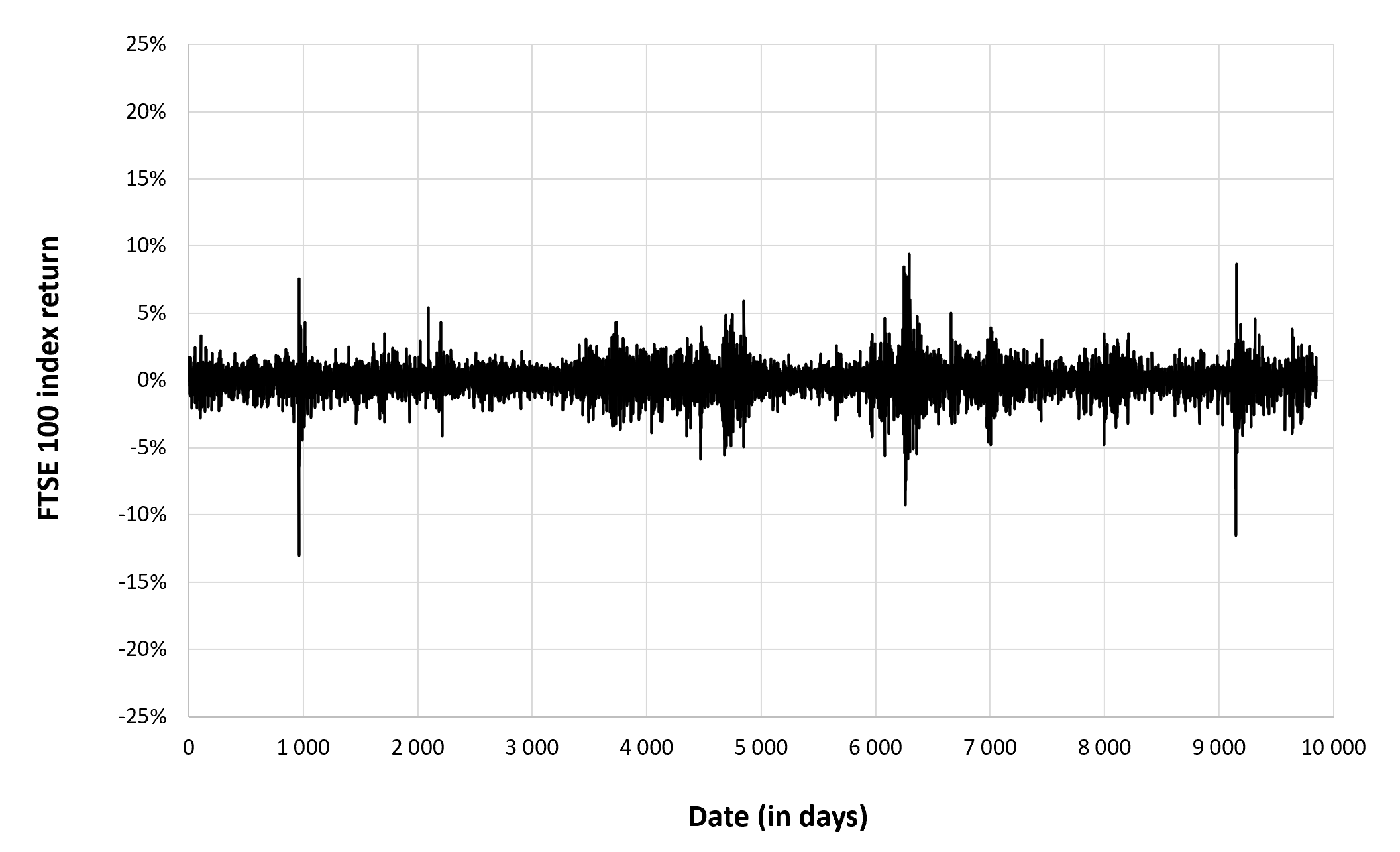
Figure 3 below represents the evolution of the monthly trading volume of Bitcoin over the period October 2014 – July 2023.
Figure 3. Evolution of the trading volume of Bitcoin
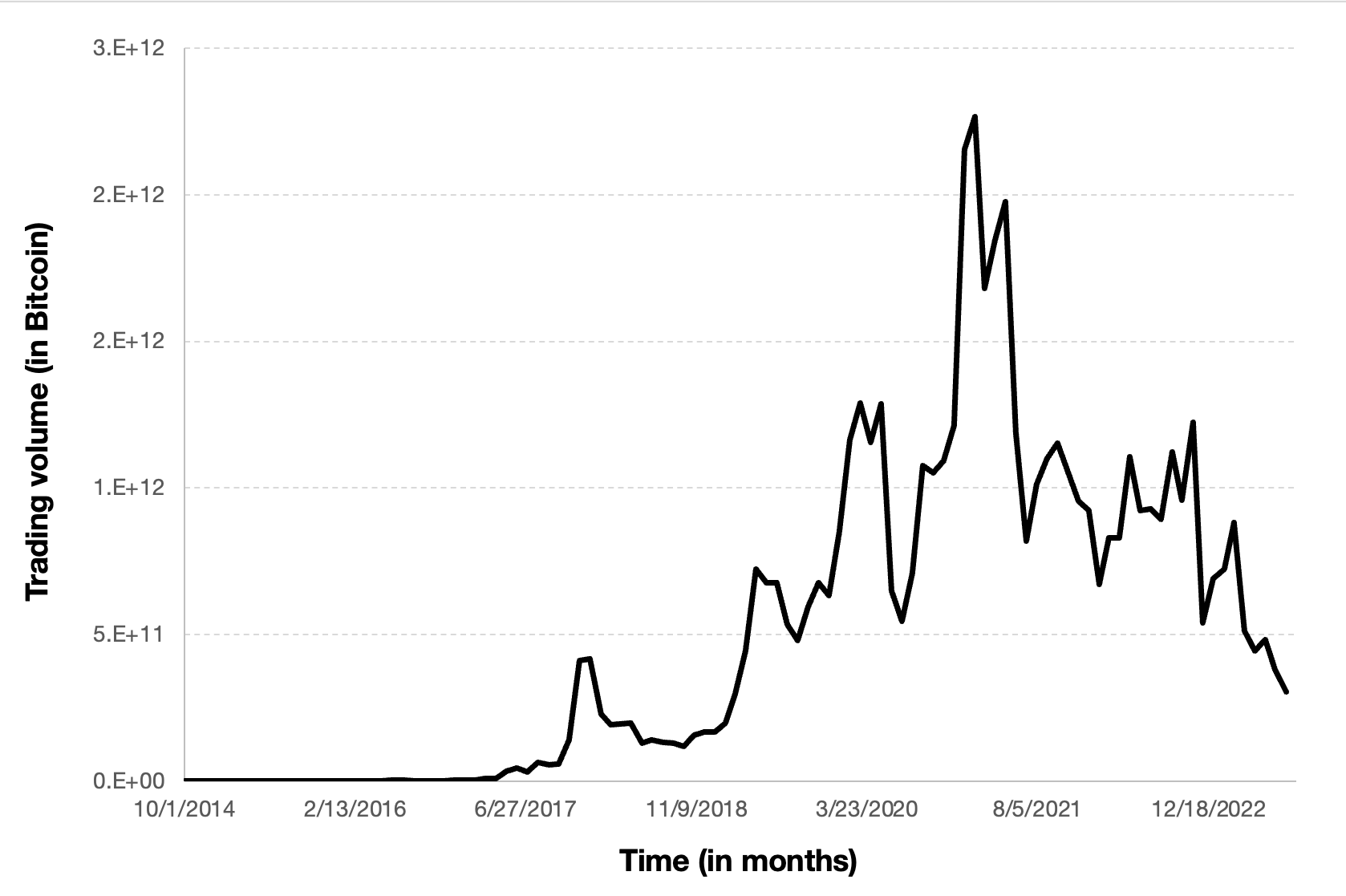
Source: computation by the author (data source: Yahoo! Finance).
Bitcoin data
You can download the Excel file with Bitcoin data used in this post as an illsutration.
Python code
You can download the Python code used to download the data from Yahoo! Finance.
Python script to download Bitcoin historical data and save it to an Excel sheet:
import yfinance as yf
import pandas as pd
# Define the ticker symbol and date range
ticker_symbol = “BTC-USD”
start_date = “2020-01-01”
end_date = “2023-01-01”
# Download historical data using yfinance
data = yf.download(ticker_symbol, start=start_date, end=end_date)
# Create a Pandas DataFrame
df = pd.DataFrame(data)
# Create a Pandas Excel writer object
excel_writer = pd.ExcelWriter(‘bitcoin_historical_data.xlsx’, engine=’openpyxl’)
# Write the DataFrame to an Excel sheet
df.to_excel(excel_writer, sheet_name=’Bitcoin Historical Data’)
# Save the Excel file
excel_writer.save()
print(“Data has been saved to bitcoin_historical_data.xlsx”)
# Make sure you have the required libraries installed and adjust the “start_date” and “end_date” variables to the desired date range for the historical data you want to download.
APIs
Calculating the total number of Bitcoins in circulation over time
Access – Bitcoin Blockchain data
By running a Bitcoin node or by using blockchain data providers like Blockchain.info, Blockchair, or a similar service.
Extract Block Data: Once you have access to the blockchain data, you would need to extract information from each block. Each block contains a record of the transactions that have occurred, including the creation (mining) of new Bitcoins in the form of a “Coinbase” transaction.
Calculate Cumulative Supply: You can calculate the cumulative supply of Bitcoins by adding up the rewards from each block’s Coinbase transaction. Initially, the block reward was 50 Bitcoins, but it halves approximately every four years due to the Bitcoin halving events. So, you’ll need to account for these halving in your calculations.
Code – python
import requests
# Replace ‘YOUR_API_KEY’ with your CoinMarketCap API key
api_key = ‘YOUR_API_KEY’
# Define the endpoint URL for CoinMarketCap’s API
url = ‘https://pro-api.coinmarketcap.com/v1/cryptocurrency/quotes/latest’
# Define the parameters for the request
params = {
‘symbol’: ‘BTC’,
‘convert’: ‘USD’,
‘CMC_PRO_API_KEY’: api_key
}
# Send the request to CoinMarketCap
response = requests.get(url, params=params)
# Parse the response JSON
data = response.json()
# Extract the circulating supply from the response
circulating_supply = data[‘data’][‘BTC’][‘circulating_supply’]
print(f”Current circulating supply of Bitcoin: {circulating_supply} BTC”)
## Replace ‘YOUR_API_KEY’ with your actual CoinMarketCap API key.
Why should I be interested in this post?
Cryptocurrency data is becoming increasingly relevant in these fields, offering opportunities for research, data analysis skill development, and even career prospects. Whether you’re aiming to conduct research, stay informed about the evolving financial landscape, or simply enhance your data analysis abilities, understanding how to access and work with crypto data is an asset. Plus, as the cryptocurrency industry continues to grow, this knowledge can open new career paths and improve your personal finance decision-making. In a rapidly changing world, diversifying your knowledge with cryptocurrency data acquisition skills can be a wise investment in your future.
Related posts on the SimTrade blog
▶ Alexandre VERLET Cryptocurrencies
▶ Youssef EL QAMCAOUI Decentralised Financing
▶ Hugo MEYER The regulation of cryptocurrencies: what are we talking about?
Useful resources
APIs
CoinMarketCap Source of API keys and program
CoinGecko Source of API keys and Programs
CryptoNews Source of API keys and Programs
Data sources
Yahoo! Finance Historical data for Bitcoin
Coinmarketcap Historical data for Bitcoin
Blockchain.com Market Data and charts on Bitcoin history
About the author
The article was written in October 2023 by Snehasish CHINARA (ESSEC Business School, Grande Ecole Program – Master in Management, (2022-2024).