Capital Guaranteed Products
In this article, Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2023) explains how capital guaranteed products are built.
Motivation for investing in capital-guaranteed products
In order to invest the surplus of the firm liquid assets, corporate treasurers take into account the following characteristics of the financial instruments: performance, risk and liquidity. It is a common practice that some corporate investment strategies require that the investment capital should at least be guaranteed. The sacrifice of this no-loss guarantee is limited return in case of appreciation of the underlying asset price.
Capital-guaranteed (or capital-protected) products are one of the most secure forms of investment, usually in the form of certificates. They provide a guarantee that a specified minimum amount (usually 100 per cent of the issuance price) will be repaid at maturity. They are suitable particularly for risk-averse investors who wish to hold the products through to maturity and are not prepared to bear any loss that might exceed the level of the guaranteed repayment.
Performance
Let us consider a capital-guaranteed product with the following characteristics:
Table 1. Characteristics of the capital-guaranteed products
| Notional amount | EUR 1,000,000.00 |
| Underlying asset | CAC40 index |
| Participation rate | 40% |
| Minimum amount guarantee | 100% of the initial level |
| Effective date | February 01, 2022 |
| Maturity date | July 30, 2022 |
We also have the following information about the market:
Table 2. Market information
| Risk-free rate (annual rate) | 8% |
| Implied volatility (annualized) | 10% |
In case of depreciation of the underlying index, the return of the product remains zero, which means the original capital invested is guaranteed (or protected). In case of appreciation of the underlying index, the product only yields 40% of the return of the underlying index. The following chart is a straightforward illustration of the performance structure of this product.
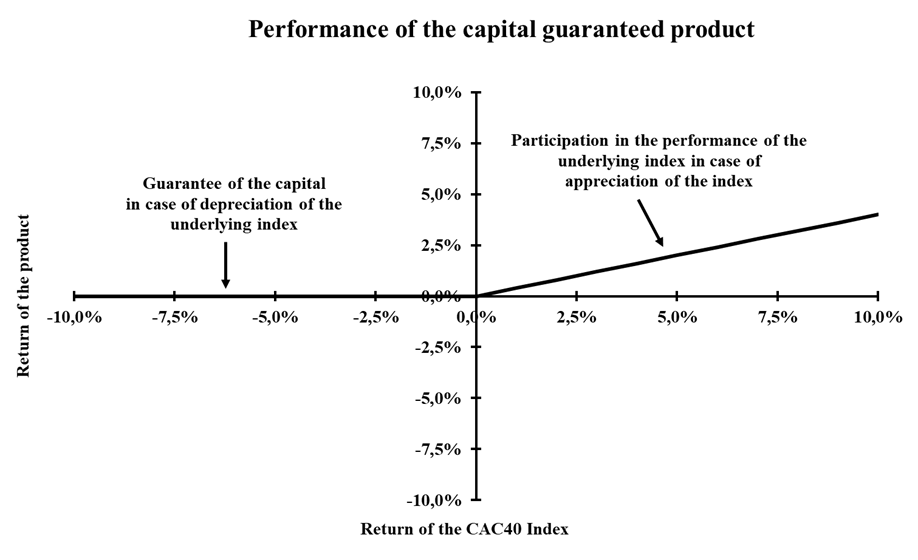
Construction of a capital guaranteed product
We can decompose a capital-guaranteed product into three parts:
- Investment in the risk-free asset that would yield the guaranteed capital at maturity
- Investment in a call option that guarantees participation in the appreciation of the underlying asset
- Margin of the bank

Investment in the risk-free asset
The essence of the capital guarantee is realized by investing a part of the initial capital in the risk-free asset and obtaining the amount of the guaranteed capital at maturity. Given the amount of the capital to be guaranteed and the risk-free rate, we can calculate the amount to be invested in risk-free asset: 1,000,000/(1+0.08)^0.5 =962,250.45 €
Investment in the call option
To realize the upside exposure, call options are a perfect vehicle. With a notional amount of 1,000,000 € and a maturity of 6 months, an at-the-money call option would cost 41,922.70 € (calculated with the Black-Scholes-Merton formula). Since the participation rate is 40%, the amount to be invested in the call option would be 16,769.08 € (= 40% * 41,922.70 €).
Margin of the bank
The margin of the bank is equal to the difference between the original capital and the two parts of the investment. In this case, the margin is 20,980.47 € (= 1,000,000.00 € – 962,250.45 € – 16,769.08 €)
If we compress the margin, there would be more capital available to invest in the call option, thus increasing the participation rate. In the case of zero margin, we obtain the maximum participation rate. In this scenario, the maximum participation rate would be 90.05% (= (1,000,000.00 € – 962,250.45 €) / 41,922.70 €).
Sensitivity to variations of the marketplace
Considering the two parts of the investment constituting the capital-guaranteed product, we can see that the risk-free rate and the volatility of the underlying asset are the two major factors influencing the pricing of this product. Here let us focus on the maximum participation rate as a proxy of the value of the product to the buyer of the product.
The effect of the risk-free rate could be ambiguous at the first glance. On one hand, if the risk-free rate rises, there needs to be less capital invested in the risk-free asset and there would be therefore more capital to be placed in purchasing the call options. On the other hand, if the risk-free rate rises, the call option value rises as well. With the same amount of capital, fewer call options could be purchased. However, the largest portion of the original capital is invested in the risk-free asset and the impact on this regard is more important. Overall, a rising risk-free rate has a positive impact on the participation rate.
The effect of the volatility of the underlying asset, however, is clear. Rising volatility has no impact on the risk-free investment in the framework of our hypotheses. It, however, raises the value of the call options, which means that fewer options could be purchased with the same amount of capital. Overall, rising volatility has a negative impact on the participation rate.
Statistical distribution of the return
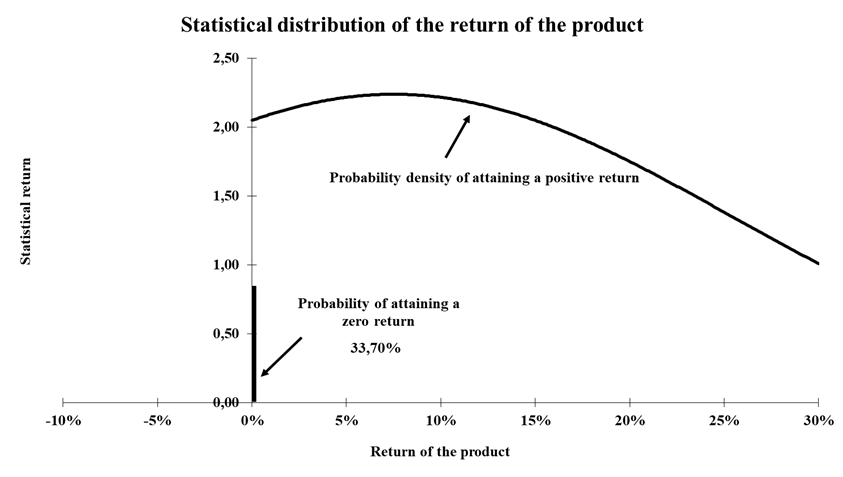
The statistical distribution of the return of the instrument is mixed by two parts: the discrete part equal to 0 corresponding to the case of depreciation of the underlying asset; and the continuous part of positive return. Based on a Gaussian assumption for the statistical distribution, we can calculate the probability mass of the depreciation of the underlying asset is 33.70%. In the continuous part, the return follows a Gaussian statistical distribution, with a mean equal to the periodic return over the participation rate and a standard deviation equal to periodic implied volatility over the participation rate, if the Gaussian assumption prevails.
Risks and constraints
Liquidity risk
Being exotic financial instruments, capital-guaranteed products are not traded in standard exchanges. By construction, these products can normally only be redeemed at maturity and therefore are less liquid. There could be, however, early redemption clauses involved to mitigate the long-term liquidity risks. Investors should be aware of their liquidity needs before entering into a position in this product.
Counterparty risk
Similar to all other over-the-counter (OTC) transactions, there is no mechanism such as a central clearing counterparty (CCP) to ensure the timeliness and integrity of due payments. In case of financial difficulty including the bankruptcy of the issuer, the capital guarantee would be rendered worthless. It is therefore highly recommended to enter into such transactions with issuers of higher ratings.
Limited return
It is worth noting that capital-guaranteed products have weak exposure to the appreciation of the underlying asset. In this case, for a probability of 33.70%, there would be a return of zero, which is lower than investing directly in the risk-free security.
In order to mitigate this limit, the issuer could modify the level of guarantee to a lower level than 100%. This allows the product to have more exposure to the upside movement of the underlying asset with a relatively low risk of capital loss. To realize this involves entering positions of out-of-the-money call options.
Taxation and fees
In many countries, the return of capital-guaranteed products is considered as ordinary income, instead of capital gains or tax-advantaged dividends. For example, in Switzerland, it is not recommended to buy such a product with a long maturity, since the tax burden, in this case, could be higher than the “impaired” return of the product.
Moreover, fees for such products could be higher than exchange-traded funds (ETFs) or mutual funds. This part of investment cost should also be taken into account in making investment decisions.
Download the Excel file to analyze capital-guaranteed products
You can find below an Excel file to analyze capital-guaranteed products.
Why should I be interested in this post?
As a family of investments that is often used in corporate treasury management, it is important to understand the mechanism and structure of capital-guaranteed products. It would be conducive for future asset managers, treasurer managers, or structurers to make the appropriate and optimal investment decisions.
Related posts on the SimTrade blog
▶ Shengyu ZHENG Barrier options
▶ Shengyu ZHENG Reverse convertibles
Resources
Books
Cox J. C. & M. Rubinstein (1985) “Options Markets” Prentice Hall.
Hull J. C. (2005) “Options, Futures and Other Derivatives” Prentice Hall, 6th edition.
Articles
Black F. and M. Scholes (1973) The Pricing of Options and Corporate Liabilities Journal of Political Economy, 81(3): 637-654.
Lacoste V. and Longin F. (2003) Term guaranteed fund management: the option method and the cushion method Proceeding of the French Finance Association, Lyon, France.
Merton R. (1974) On the Pricing of Corporate Debt Journal of Finance, 29(2): 449-470.
Websites
longin.fr Pricer for standard equity options – Call and put
Euronext www.euronext.com: website of the Euronext exchange where the historical data of the CAC 40 index can be downloaded
Euronext CAC 40 Index Option: website of the Euronext exchange where the option prices of the CAC 40 index are available
Six General information about capital protection without a cap: website of the Swiss stock exchange where information of various financial products are available.
About the author
The article was written in February 2023 by Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2023).


