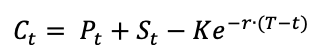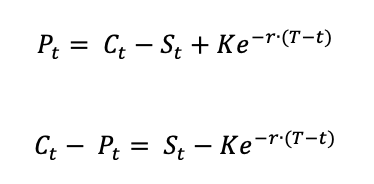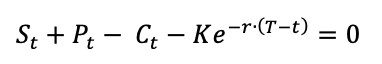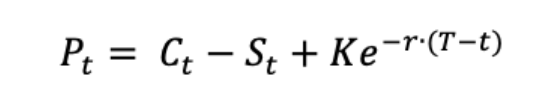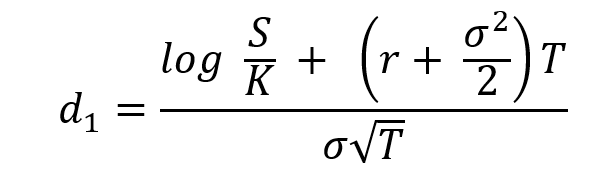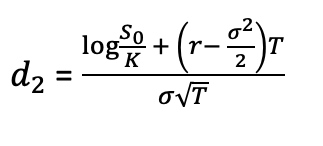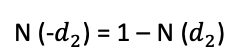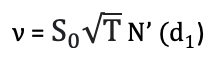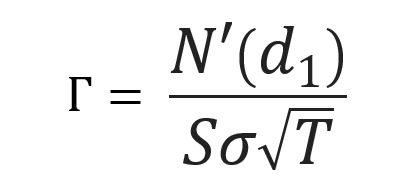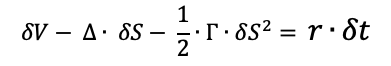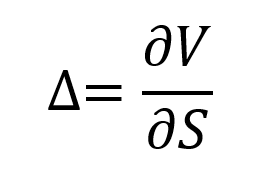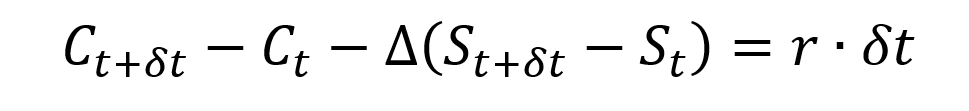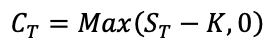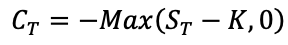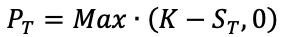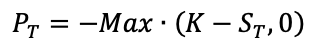Plain Vanilla Options

June 4, 2024August 23, 2021 by Jayati WALIA

Plain Vanilla Options

In this article, Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) presents plain vanilla options.

Introduction

An option contract is a financial derivative that gives its holder the right (but not the obligation) to trade an underlying asset at a price and a date set in advance.

In finance, plain vanilla refers to the most basic version of any financial instrument with standard features. Thus, a plain vanilla option simply refers to a contract that provides the option to buy or sell an underlying stock (or any financial asset) at a fixed price (known as the exercise/strike price) at an expiration date in the future. The expiration date (or maturity) of the option is the date when the holder can exercise her option if she wants.

In the US, options were first traded on an exchange on 26th April 1973. The Chicago Board Options Exchange (CBOE) was the first to create standardized, listed options. Today, there are over 50 exchanges worldwide that trade options.

When an option is bought, its holder pays a fixed amount to the option writer as the cost for the flexibility of trading that the option provides. This cost, which is essentially the value of an option (and the margin taken by the issuer), is known as the premium. The premium depends on the characteristics of the option like the strike price and the maturity, and on market data like the price of the underlying asset and especially its volatility. Many different underlying assets can be traded through options including stocks, bonds, commodities, foreign currencies.

Types of options

Vanilla options are of two types: call and put.

Call options

The holder of a call option has the right to buy a particular asset at a strike price K at maturity T. If the asset price at maturity denoted by S_T is higher than K, then it is beneficial for the call option holder to exercise his option at time T as the price set in the call option contract K is lower than the market price S_T. If the asset price at maturity S_T is lower than K, then it is not beneficial for the call option holder to exercise his option at time T as the price set in the call option contract K is higher than the market price S_T; he is then better off to buy the asset on the market at price S_T than at price K.

For example, consider a call option on BNP Paribas stock with a strike price of €50 and a maturity date March 31^st. The holder of this call option thus has the right but not the obligation to buy one BNP Paribas stock for €50 at maturity. He will exercise his option on March 31^st if and only if the stock price is higher than €50.

The equation below gives the pay-off function of a call option that is the value of the call option at maturity T denoted by C_T as a function of the price of the underlying asset S_T.

Payoff formula for a call option

Figure 1 gives a graphical representation of the pay-off function of a call option that is the value of the call option at maturity T as a function of the price of the underlying asset at maturity T, S_T, for a given strike price (equal to €50 in the figure).

Figure 1. Pay-off function of a call option

Payoff for a call option

Put options

Similarly, the holder of a put option has the right to sell a particular asset at a strike price K at maturity T. If the asset price at maturity denoted by S_T is higher than K, then it is beneficial for the put option holder not to exercise his option at time T as the price set in the put option contract K is lower than the market price S_T; he is then better off to sell the asset on the market at price S_T than at price K. If the asset price at maturity S_T is lower than K, then it is beneficial for the put option holder to exercise his option at time T as the price set in the put option contract K is higher than the market price S_T.

For example, consider a put option on BNP Paribas stock with a strike price of €50 and a maturity date March 31^st. The holder of this put option thus has the right but not the obligation to sell one BNP Paribas stock for €50 at maturity. He will exercise his put option on March 31^st if and only if the stock price is lower than €50.

The equation below gives the pay-off function of a put option that is the value of the put option at maturity T denoted by P_T as a function of the price of the underlying asset S_T.

Payoff formula for a put option

Figure 2 gives a graphical representation of the pay-off function of a put option that is the value of the put option at maturity T as a function of the price of the underlying asset S_T for a given strike price (equal to €50 in the figure).

Figure 2. Pay-off function of a put option

Payoff for a put option

Types of exercise

Options can be categorized based on their exercise restrictions.

American options

American options have the most flexible arrangement allowing holders to exercise their options at any time prior to the expiration date. They are widely traded over listed exchanges.

European options

European options provide less flexibility and allow holders to exercise options on only one specific date, which is the expiration date. They thus have a lower value compared to American options and are generally traded OTC.

Bermudan options

There are also Bermudan options that allow exercise of options on a set of specific dates before the expiration and thus provide holders a level of flexibility midway between American and European Options.

Moneyness

Options can also be characterized by their “moneyness” which compares the current price of the underlying asset to the option strike.

In-the-money options

An option with a positive intrinsic value is said to be ‘in the money’. This is the case for a call option if the current market price of the asset is higher than the strike price, and similarly for a put option if the current market price of the asset is lower than the strike price.

Out-of-the-money options

An option with a zero intrinsic value is said to be ‘out of the money’. This is the case for a call option if the current market price of the asset is lower than the strike price, and similarly for a put option if the current market price of the asset is higher than the strike price.

At-the-money options

An option with a strike price close or equal to the current market price is said to be ‘at the money’.

Option writers

The above discussion mainly revolves around option purchasers. However, there is also someone who is liable to sell (for a call) or buy (for a put) the underlying security whenever any holder exercises an option. The writer of an option is the person who is obligated to buy/sell the underlying in case of a call/put exercise. As a counterpart, the writer also receives the option premium from the holder.

The best-case scenario for a writer would be that the option is not exercised by its holder as the option remains out of the money (the writer earning the premium without being obliged to pay the cash flow at maturity). However, option writers are exposed to downside risks especially if the options they write are not covered i.e., holding a long or short position already in the underlying security depending on the option written.

Benefits

For traders with strong market views looking to leverage benefits from small to medium-term fluctuations in market price, buying options is an efficient means to offset their risk exposure. The buyer only risks a small amount of investment, and the downside is only limited to the initial premium whereas the upside is a high payoff if the speculation is in her/his favor. The traders can also take up multiple positions in different assets through options and leverage trade opportunities with profitable positions covering more than the hedging costs.

Option Trading

Most vanilla options are traded through exchanges that make it convenient to match buyers with sellers and vice versa. Trading of standardized contracts also promotes liquidity of the instruments in the market. Vanilla options generally come in series of standardized strike prices and expiration dates. For instance, for an option contract on an Apple Inc. stock (AAPL) expiring on 20^th August 2021, the offered strike prices are $115, $120, $125, $130 and so on. Similarly, the expiration dates for listed stock options is generally the third Friday of the month in which the contract expires. If the Friday falls on a holiday, the expiration date becomes Thursday immediately before the third Friday.

Option pricing

The value an option is known at maturity as it is given by the contract. But what is the value of an option at the time of its issuance or at a time before maturity? Many mathematical models have been developed to answer this question. The most famous model is the Black-Scholes-Merton option pricing model. It uses a Brownian motion to model the behavior of stock market prices.

Use of options

Hedging

Options are commonly used in hedging. For instance, you can purchase an option on a stock to limit your losses to say 15% of your position, should the stock decline more than that during the option period.

Speculation

If one has a strong view about the potential market direction of an underlying security, one can make great returns on exploiting options, provided the view was right. This is essentially speculation in option trading. For instance, if you have a bullish opinion regarding a stock, you can purchase a call option on it that will allow you to purchase the stock at the strike price that will be lower than the future price (hopefully!). Thus, if you are right, you could exercise the option and your payoff would be the price difference between the stock price and the strike price. If you are wrong, you lose out on the premium you paid for the option.

Volatility

The volatility of the underlying asset affects positively option prices: stocks with higher volatility have more expensive option contracts that those with low volatility. In fact, the implied volatility (IV) of an option is that value of the volatility of the underlying instrument for which an option pricing model (such as the Black-Scholes-Merton model) will return a theoretical value equal to the current market price of that option. Hence, when the implied volatility increases, the price of options increases as well, assuming all other factors remain constant. When the implied volatility increases after a trade has been placed, it is good news for the option owner and, conversely bad news for the seller. Inversely, when the implied volatility decreases after a trade has been placed, it is bad news for the option owner and, conversely good news for the seller.

Note that the implied volatility tends to depend on the strike price and maturity date of the options for a given underlying asset. Once the implied volatility for the at-the-money contracts is determined in any given expiration month, market makers use pricing models and volatility skews to calculate implied volatility at other strike prices that are less heavily traded. So, every option has an associated volatility and risk profiles can vary drastically among options. Traders may at times balance out the risk of volatility by hedging one option with another.

Thus, it is essential to interpret and analyze risks before venturing into option trading. There are also many strategies that can be applied to vanilla options in order to benefit better and limit risk such as long and short calls/puts, bull and bear spreads, straddles and strangles, butterflies, condors among many.

Useful Resources

Nasdaq Historical data for Apple stock

AVATRADE What are vanilla options

TheStreet Options Trading

About the author

The article was written in August 2021 by Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).

Derivatives Market

August 23, 2021 by Jayati WALIA

Derivatives Market

In this article, Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) presents an overview of derivatives market.

Introduction

A financial market refers to a marketplace where various kinds of financial securities such as stocks, bonds, commodities, etc. are traded. The term ‘market’ can also refer to exchanges that are legal organizations that facilitate the trade of financial securities between buyers and sellers. In any case, these markets are categorized based of the type of financial securities that are traded through them. One such financial market is the Derivatives Market.

Derivatives market thus refers to the financial marketplace where derivative instruments such as futures, forwards and options contracts are traded between counterparties.

It was during the 1980s and 1990s that the financial markets saw a major growth in the trade of derivatives. A derivative is a financial instrument whose value is derived from the value of an underlying asset such as stocks, bonds, currencies, commodities, interest rates and/or different market indices. These underlying assets have fluctuating prices and returns, and derivatives provides a means to investors to reduce the risk exposure and leverage profits on these assets. Thus, derivatives are an essential class of financial instruments and central to the modern financial markets providing not just economic benefits but also resilience against risks. The most common derivatives include futures, forwards, options and swap contracts.

As per the European Securities and Markets Authority (ESMA), derivatives market has grown impressively (around 24 percent per year in the last decade) into a truly global market with over €680 trillion of notional amount outstanding. The interest rate derivatives (IRDs) accounted for 82% of the total notional amount outstanding followed by currency derivatives at 11%.

Main types of derivative contracts

Derivatives derive their value from an underlying asset, or simply an ‘underlying’. There is a wide range of financial instruments that can be an underlying for a derivative such as equities or equity index, fixed-income instruments, foreign currencies, commodities, and even other securities. And thus, depending on the underlying, derivative contracts can derive their values from corresponding equity prices, interest rates, foreign exchange rates, prices of commodities and probable credit events. The most common types of derivative contracts are elucidated below:

Forwards and Futures

Forward and futures contracts share a similar feature: they are an agreement between two parties to buy or sell a specified quantity of an underlying asset at a specified price (or ‘exercise price’) on a predetermined date in the future (or ‘expiration date’). While forwards are customized contracts i.e., they can be tailor-made according to the asset being traded, expiry date and price, and traded Over-the-Counter (OTC), futures are standardized contracts traded on centralized exchanges. The party that buys the underlying is said to be taking a long position while the party that sells the asset takes a short position and both parties are obligated to fulfil their part of the contract.

Options

An option contract is a financial derivative that gives its holder the right (but not the obligation) to trade an underlying asset at a price set in advance irrespective of the market price at maturity. When an option is bought, its holder pays a fixed amount to the option writer as cost for this flexibility of trading that the option provides, known as the premium. Options can be of the types: call (right to buy) or put (right to sell).

Swaps

Swaps are agreements between two counterparties to exchange a series of cash payments for a stated period of time. The periodic payments charged can be based on fixed or floating interest rates, depending on contract terms decided by the counterparties. The calculation of these payments is based on an agreed-upon amount, called the notional principal amount (or just notional).

Exchange-traded vs Over-the-counter Derivatives Market

Exchange-traded derivatives markets

Exchange-traded derivatives markets are standardized markets for derivatives trading and follows rules set by the exchange. For instance, the exchange sets the expiry date of the derivatives, the lot-size, underlying securities on which derivatives can be created, settlement process etc. The exchange also performs the clearing and settlement of trades and provide credit guarantee by acting as a counterparty for every trade of derivatives. Thus, exchanges provide a transparent and systematic course of action for any derivatives trade.

Over-the-counter markets

Over-the-counter (also known as “OTC”) derivatives markets on the other hand, provide a lesser degree of regulations. They were almost entirely unregulated before the financial crisis of 2007-2008 (also a time when derivatives markets were criticized, and the blame was placed on Credit Default Swaps). OTCs are customized markets and run by dealers who hedge risks by indulging in derivatives trading.

Types of market participants

The participants in the derivative markets can be categorized into different groups namely,

Hedgers

Hedging is a risk-neutralizing strategy when an investor seeks to protect a current or anticipated position in the market by limiting their risk exposure. They can do so by taking up an offset or counter position through derivative contracts. Parties such as individuals or companies who perform hedging are called Hedgers. The hedger thus aims to eliminate volatility against fluctuating prices of underlying securities and protect herself/himself from any downsides.

Speculators

Speculation is a very common technique used by traders and investors in the derivatives market. It is based on when traders have a strong viewpoint regarding the market behavior of any underlying security and though it is risky, if the viewpoint is correct, the speculation may reward with attractive payoffs. Thus, speculators use derivative contracts with a view to make profit from the subsequent price movements. They do not have any risk to hedge, in fact, they operate at a relatively high-risk level in anticipation of profits and provide liquidity in the market.

Arbitrageurs

Arbitrage is a strategy in which the participant (or arbitrageur) aims to make profits from the price differences which arise in the investments made in the financial markets as a result of mispricing. Arbitrageurs aim to earn low risk profits by taking two different positions in the same or different contracts (across different time periods) or on different exchanges to in-cash on price discrepancies or market inefficiencies.

Margin Traders

Margin is essentially the collateral amount deposited by an investor investing in a financial instrument to the counterparty in order to cover for the credit risk associated with the investment. In margin trading, the trader or investor is not required to pay the total value of your position upfront. Instead, they only need pay the margin amount which may vary and are usually fixed by the stock exchanges considering factors like volatility. Thus, margin traders buy and sell securities over a single session and square off their position on the same day, making a quick payoff if their speculations are right.

Criticism of derivatives

While derivatives provide numerous benefits and have significantly impacted modern finance and markets, they pose many risks too. In a 2002 letter to Berkshire Hathaway shareholders, Warren Buffet even described derivatives as “financial weapons of mass destruction”.

Derivatives are more highly leveraged due to relatively relaxed regulations surrounding them, and where one may need to put up half the money or more with buying other securities, derivatives traders can get by with just putting up a few percentage points of the total value of a derivatives contract as a margin. If the price of the underlying asset keeps falling, covering the margin account can lead to enormous losses. Derivatives are thus often criticized as they may allow investors to obtain unsustainable positions that elevates systematic risk so much that it can be equated to legalized gambling. Derivatives are also exposed to counterparty credit risk wherein there is scope of default on the contract by any of the parties involved in the contract. The risk becomes even greater while trading on OTC markets which are less regulated.

Derivatives have been associated with a number of high-profile credit events over the past two decades. For instance, in the early 1990s, Procter and Gamble Corporation lost more than $100 million in transactions in equity swaps. In 1995, Barings collapsed when one of its traders lost $1.4 billion (more than twice its then capital) in trading equity index derivatives.

The amounts involved with derivatives-related corporate financial distresses in the 2000s increased even more. Two such events were the bankruptcy of Enron Corporation in 2001 and the near collapse of AIG in 2008. The point of commonality among these events was the role of OTC derivative trades. Being an AAA-rated company, AIG was being exempted from posting collateral on most of its derivatives trading in 2008. In addition, AIG was unique among CDS market participants and acted almost exclusively as credit protection seller. When the global financial crisis reached its peak in late 2008, AIG’s CDS portfolios recorded substantial mark-to-market losses. Consequently, the company was asked to post $40 billion worth of collateral and the US government had to introduce a $150 billion financial package to prevent AIG, once the world’s largest insurer by market value, from filing for bankruptcy.

Conclusion

Derivatives were essentially created in response to some fundamental changes in the global financial system. If correctly handled, they help improve the resilience of the system, hedge market risks and bring economic benefits to the users. Thus, they are expected to grow further with financial globalization. However, past credit events have exposed many weaknesses in the organization of their trading. The aim is to minimize the risks associated with such trades while enjoying the benefits they bring to the financial system. An important challenge is to design new rules and regulations to mitigate the risks and to promote transparency by improving the quality and quantity of statistics on derivatives markets.

Useful resources

Role of Derivatives in the 2008 Financial Crisis

ESMA Annual Statistical Report 2020

About the author

The article was written in August 2021 by Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).

The Black Scholes Merton Model

February 4, 2024August 19, 2021 by Akshit GUPTA

The Black-Scholes-Merton model

This article written by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) presents the Black-Scholes-Merton Model .

Introduction

Options are one of the most popular derivative contracts used by investors to hedge the risks of their portfolios, to optimize the risk profile of their positions and to make profits (or losses) by means of speculation. The value of options is known at maturity date (or expiration date) as it is given by their pay-off functions defined in their contracts. But what is the value of the option at the issuance date or any date between the issuance and the expiration? The Black-Scholes-Merton model allows to answer this question.

The Black-Scholes-Merton model is an continuous-time option pricing model used to determine the fair price or theoretical value for a call or a put option based on variable factors such as the maturity date and the strike price of the option (option characteristics), and the price of underlying asset, the volatility of the price of underlying asset, and the risk-free rate (market data). It is used to determine the price of a European call option, which refers to the option that can only be exercised on the maturity date.

History

The model was first introduced to the world by a paper titled ‘The Pricing of Options and Corporate Liabilities’ by Fischer Black and Myron Scholes and was officially published in spring 1973. Almost around the same time as Black and Scholes, Robert Merton, who was also a colleague of Scholes at MIT Sloan, presented his contributions to the model in another paper named ‘Theory of Rational Option Pricing’, where he coined the name “Black-Scholes model”. Later, Black and Scholes also published empirical tests of the model in their ‘The Valuation of Option Contracts and a Test of Market Efficiency’ paper. For their significant contribution to the world of financial markets, Merton and Black were awarded the prestigious Nobel Prize in Economic Sciences in 1997 (unfortunately Scholes had passed away in 1995 due to which he was ineligible for the Nobel Prize).

In the BSM model, the value of an option depends on the future volatility of the underlying stock rather than on its expected return. The pricing formula is based on the assumption that the price of the underlying asset follows a geometric Brownian motion.

Option pricing with BSM

The BSM model is used to find the theoretical value of a European option. The model assumes that the price of the underlying asset follows a geometric Brownian motion, which implies that the returns on the underlying asset are normally distributed. It is also assumed that there are no arbitrage opportunities, no transaction costs and the risk-free rate remains constant over time.

The BSM formula

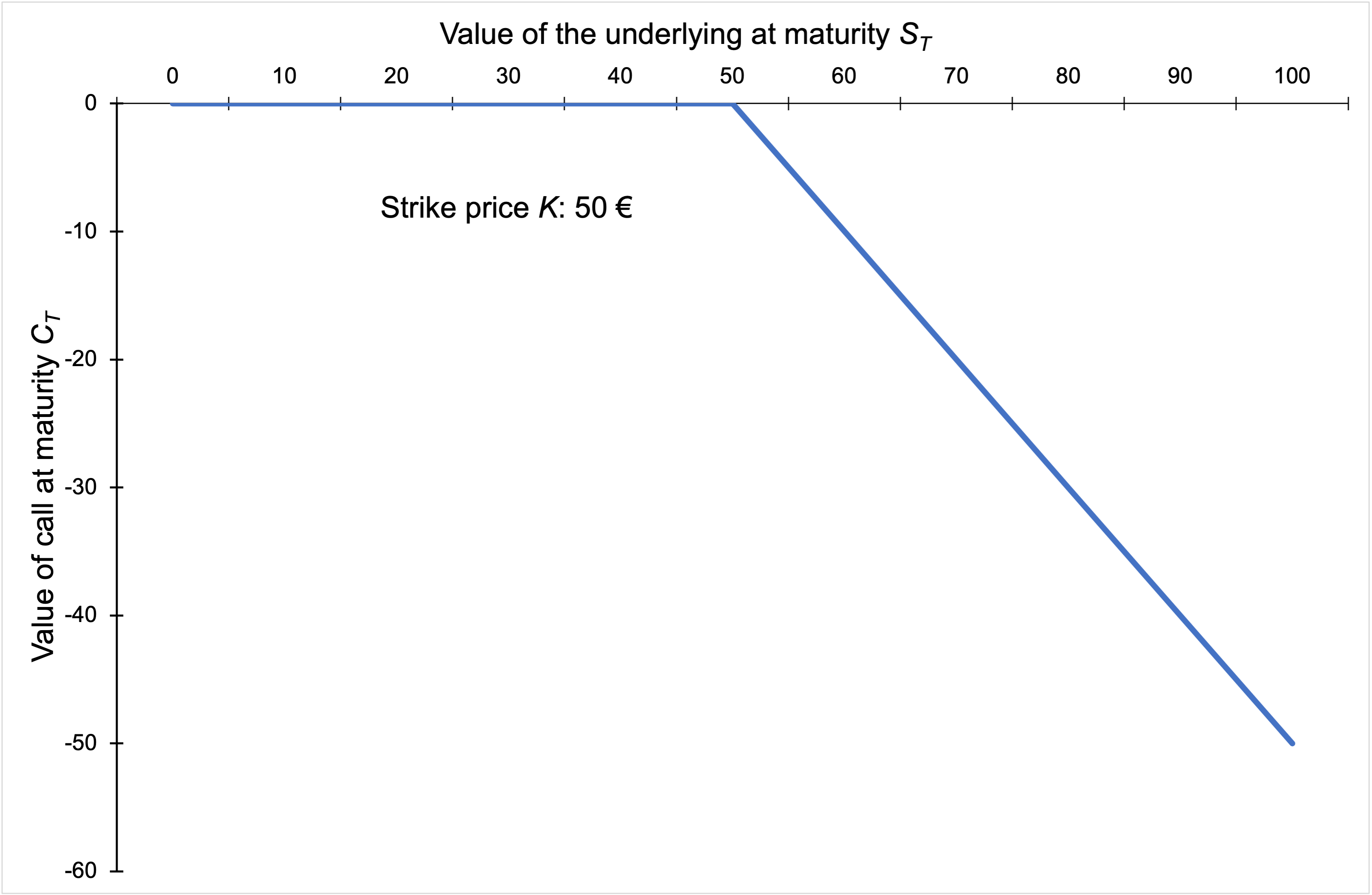
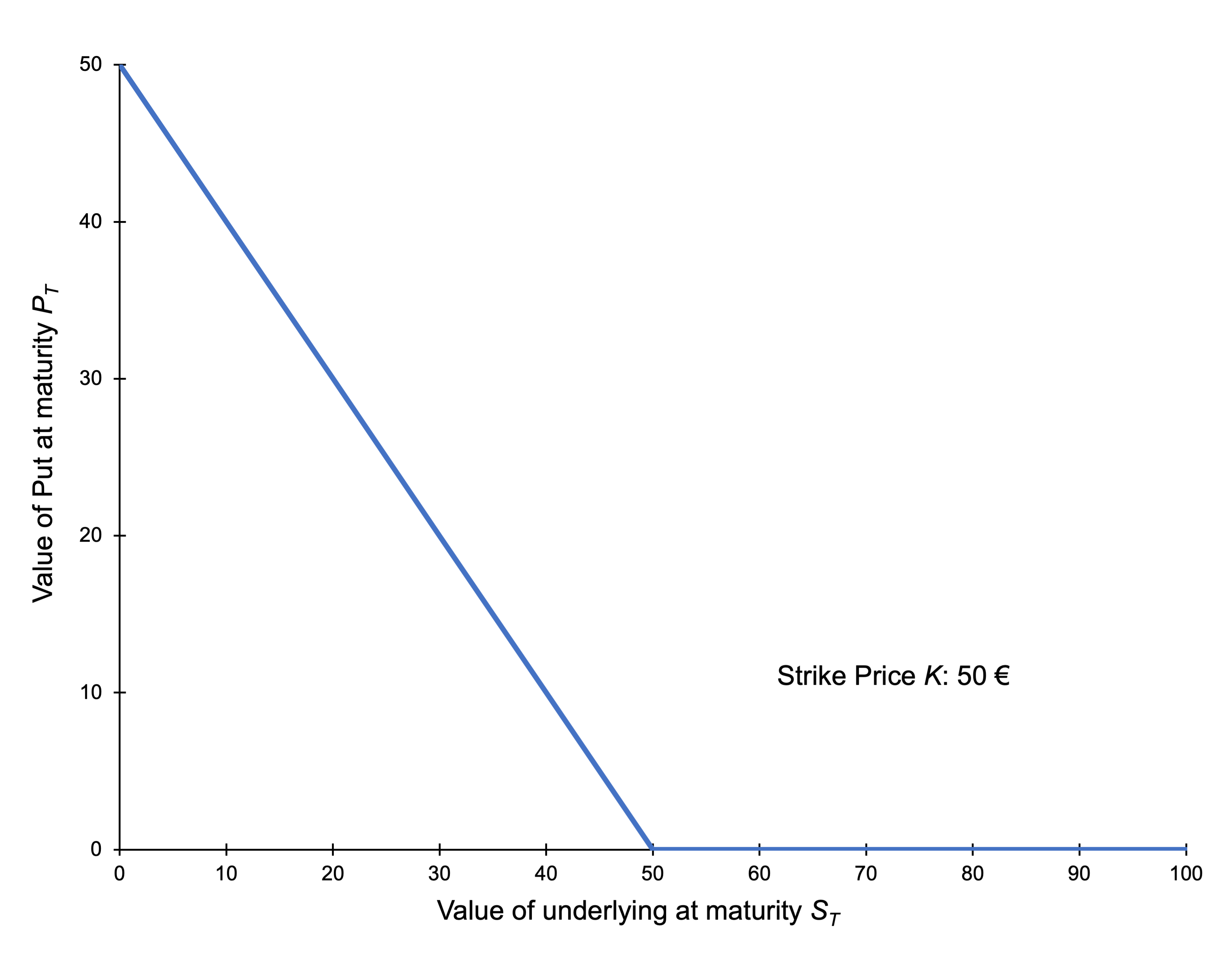
The payoffs for a call option and a put option give the value of these options at the maturity date T:

For a call option:

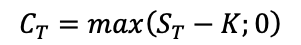
Formula for the payoff of a call option

For a put option:

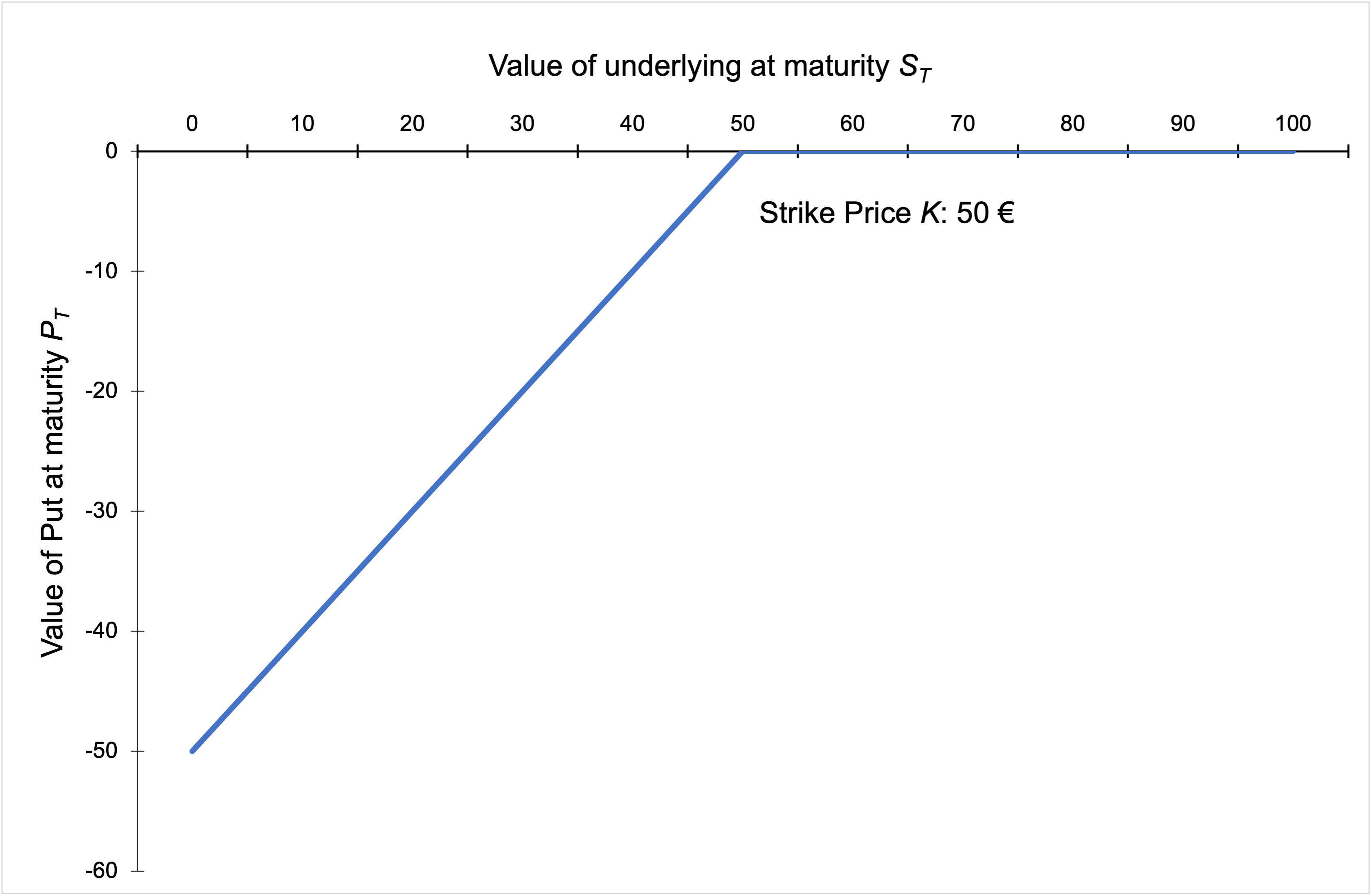
BSM Formula for the payoff of a put option

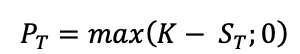
The BSM formula gives the price of European put and call options at any date before the maturity date T. The value of European call and put options for a non-dividend paying stock are given by:

For a call option:

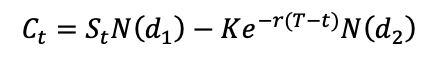
BSM formula for the call option

For a put option:

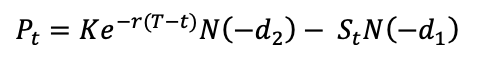
BSM formula for the put option

where,

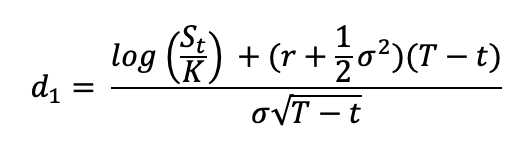
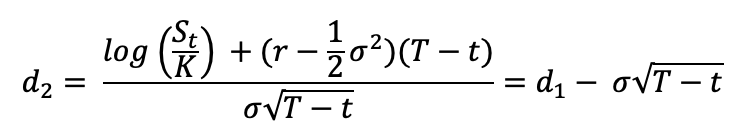
Formula for the D1 Formula for the D2

The notations used in the above formulae are described as :

S_t: price of the underlying asset at time t
t: current date (or date of calculation of option price)
T: maturity or expiry date of the option
K: strike price of the option
r: risk-free interest rate
σ: volatility (the standard deviation of the return on the underlying asset)
N(.): cumulative distribution function for a normal (Gaussian) distribution (0 ≤ N(.) ≤ 1 )

For a call option, N(+d₂) is the probability that the option will be exercised, and Ke^{(-r(T-t) )} N(+d₂) is what is expected to be paid for the underlying stock if the option is exercised, discounted to today (or the calculation date t).

Similarly, SN(+d₁) is what we can expect to receive from selling the underlying stock, if the option is exercised, also discounted to today (or the calculation date t).

For a put option, N(-d₂) is the probability that the option will be exercised, and Ke^{(-r(T-t) )} N(-d₁ ) is what is expected to be paid for the underlying stock if the option is exercised, discounted to today (or the calculation date t).

Similarly, SN(-d₁ ) is what we can expect to receive from selling the underlying stock, if the option is exercised, also discounted to today (or the calculation date t).

Note that the value of the option given by the BSM formula depends on the maturity date and the strike price of the option (option characteristics), and the price of underlying asset, and the risk-free rate (market data) and the volatility of the price of underlying asset. While the option characteristics are known and the market data are observable, the volatility of the price of underlying asset is the only unknown variable in the formula.

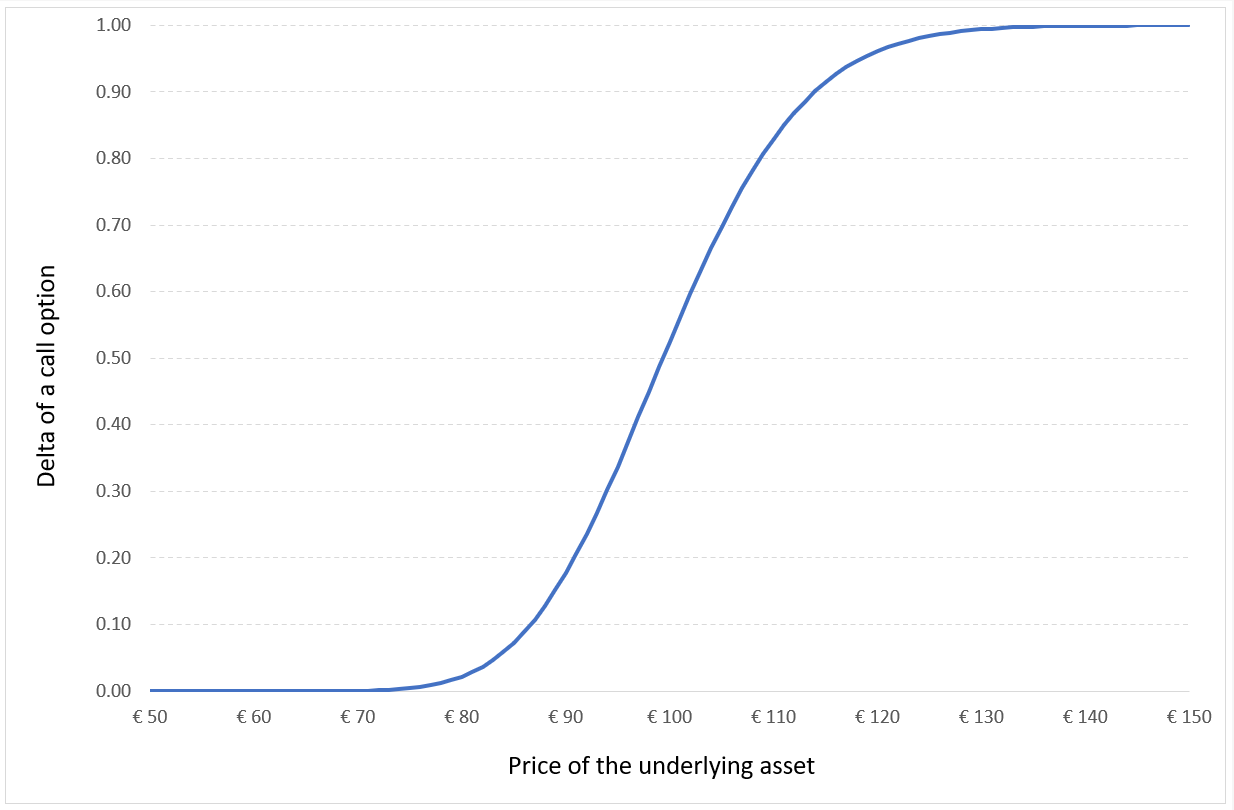
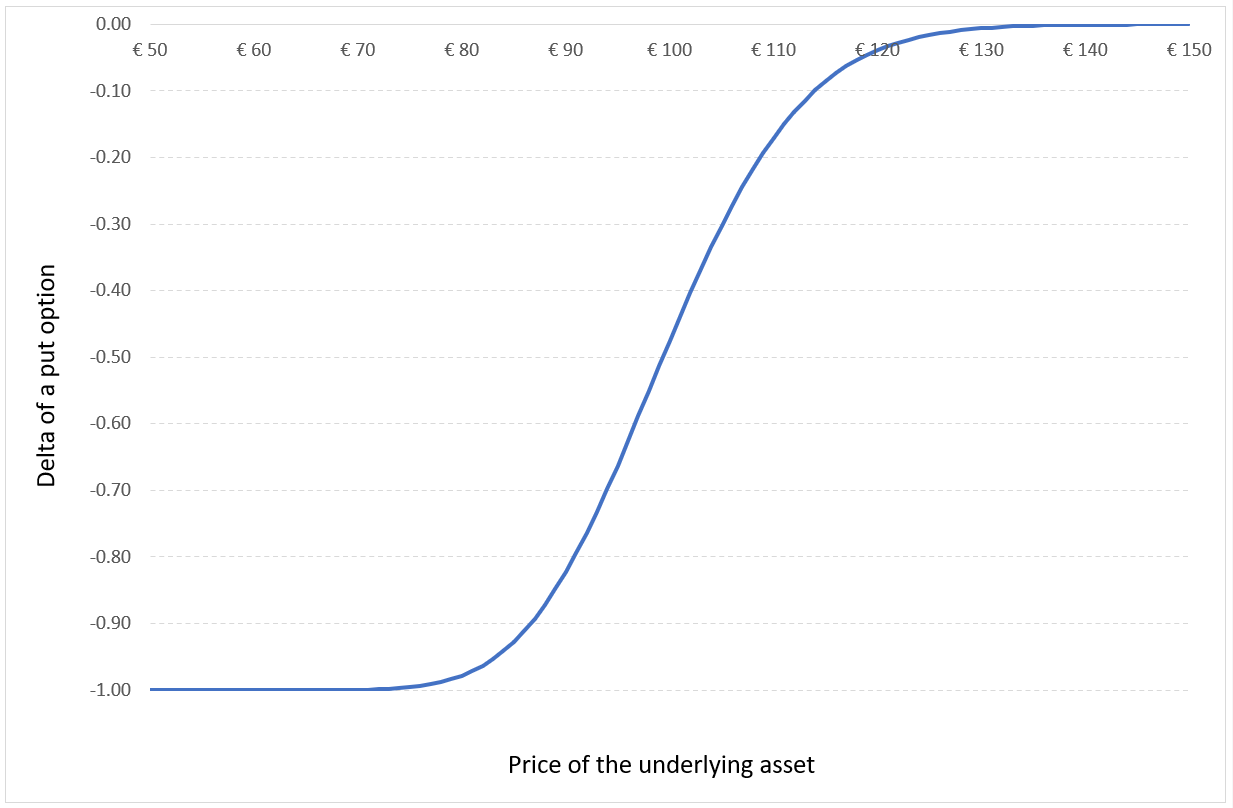
Beyond the formula itself for the option prices, the BSM model also gives a method to manage the option over time (delta hedging) as an option is equivalent (under the assumption of no arbitrage) to a portfolio composed of the underlying asset and risk-free bond.

Example – Call and Put option pricing using Black-Scholes-Merton model

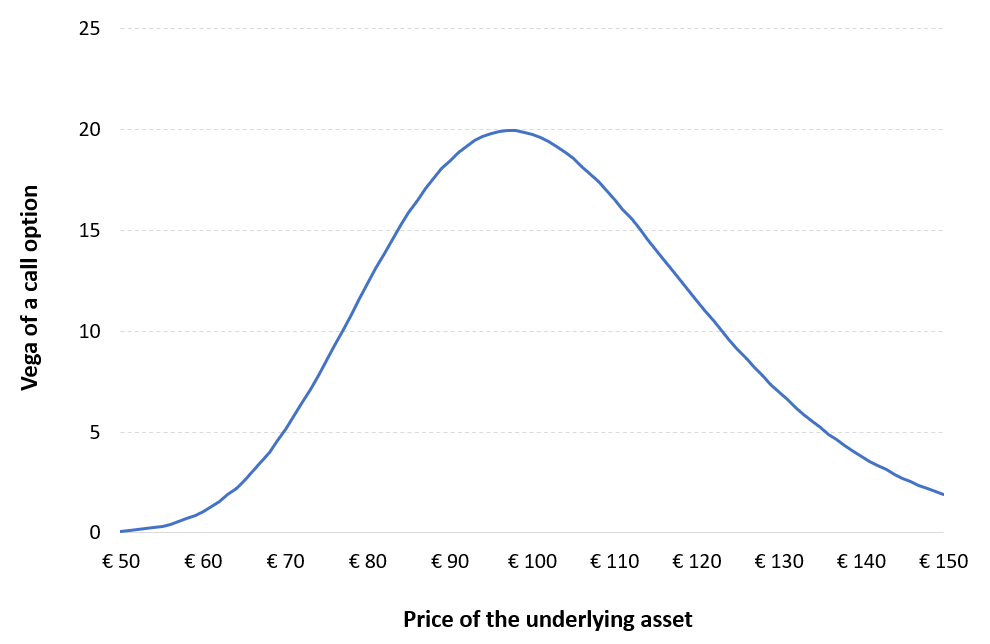
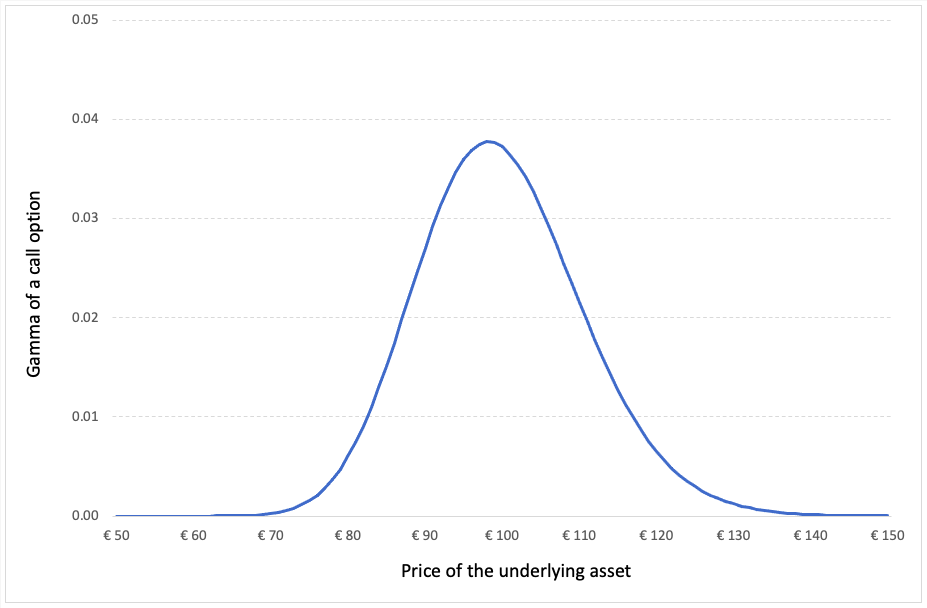
Figure 1 gives the graphical representation of the value of a call option at time t as a function of the price of the underlying asset at time t as given by the BSM formula. The strike price for the call option is 40€ with a maturity of 0.50 years. The price of the underlying asset is 50€ at time t and volatility is 40%. The risk-free rate is assumed to be 1%.

Figure 1. Call option Pricing using BSM formula 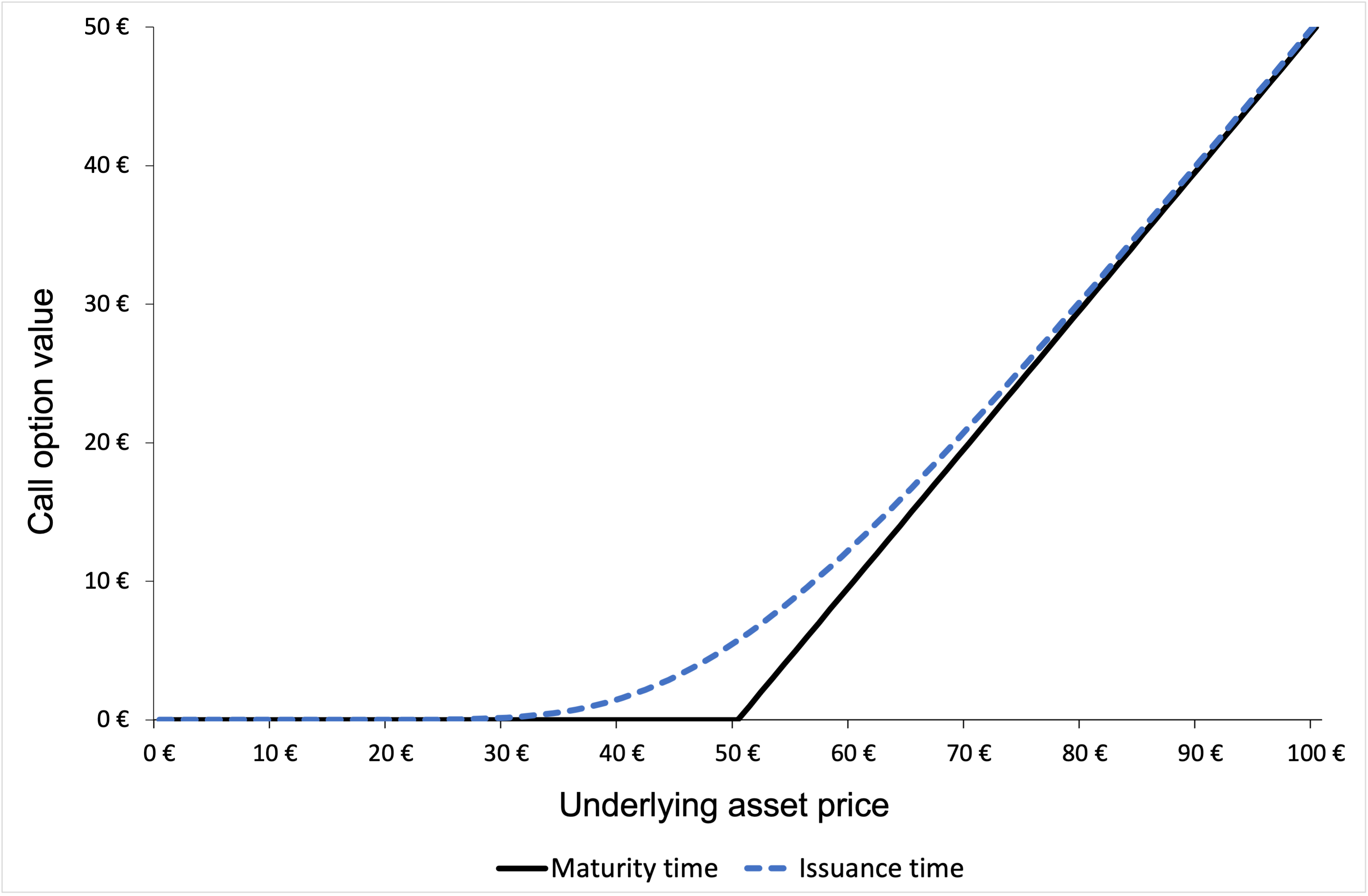Covered call
Source: computation by the author (based on the BSM model).

Figure 2 gives the graphical representation of the value of a put option at time t as a function of the price of the underlying asset at time t as given by the BSM formula. The strike price for the put option is 40€ with a maturity of 0.50 years. The price of the underlying asset is 50€ at time t and volatility is 40%. The risk-free rate is assumed to be 1%.

Figure 2. Put option Pricing using BSM formula 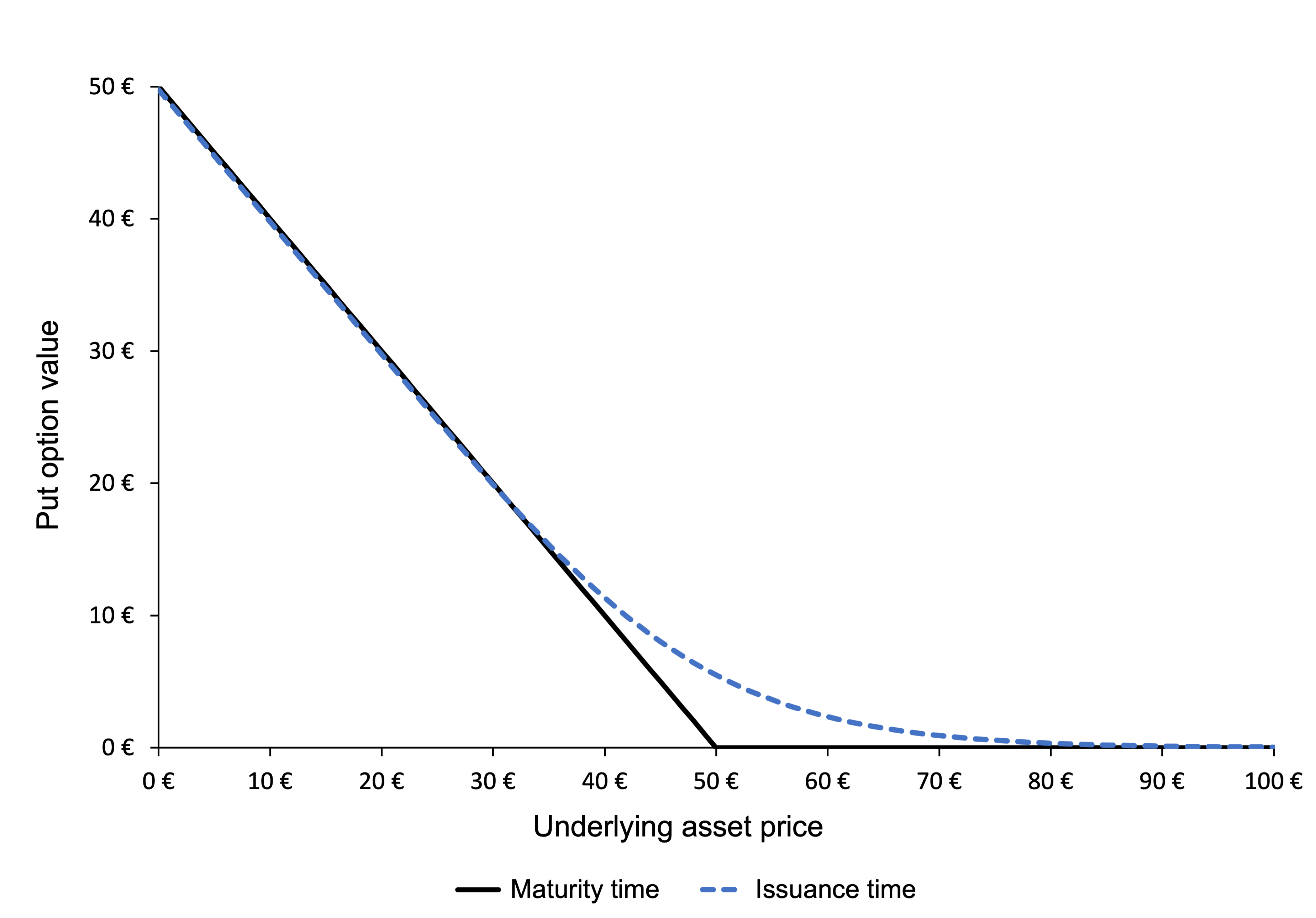Covered call
Source: computation by the author (based on the BSM model).

You can download below the Excel file used for the computation of the Call and Put option prices using the BSM Model.

Conclusion

The option-pricing model developed by Black, Scholes and Merton in 1973 provides a way of computing the prices of option contracts and has been widely used by traders since its publication. Following the seminal works by Black, Scholes and Merton, there haven been many extensions of their model, which have broadened its applicability to other instruments such as more complex options and insurance contracts.

Limitations of the BSM model

However, the model is sometimes criticized due to its weaknesses emerging from unrealistic sets of assumptions, which cause errors in estimation and model’s predictions. For instance, the BSM model assumes a constant value for volatility of the price of the underlying asset and also neglects any dividend payments from stocks which is certainly not the case in real life. Also, the model is only applicable to European options and would not be able to accurately determine the value of an American option which can be exercised at any time until the expiry date. Researchers have worked on amending the model to incorporate more realistic assumptions and have concluded that despite the model’s weaknesses, its application is still extremely useful in analyzing option prices.

Useful resources

Academic research

Black F. and M. Scholes (1973) “The Pricing of Options and Corporate Liabilities” The Journal of Political Economy, 81, 637-654.

Hull J.C. (2015) Options, Futures, and Other Derivatives, Ninth Edition, Chapter 15 – The Black-Scholes-Merton model, 343-375.

Merton R.C. (1973) “Theory of Rational Option Pricing” Bell Journal of Economics, 4, 141–183.

Wilmott P. (2007) Paul Wilmott Introduces Quantitative Finance, Second Edition, Chapter 8 – The Black Scholes Formula and The Greeks, 182-184.

About the author

Article written in August 2021 by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).

Call – Put Parity

February 10, 2026August 19, 2021 by Akshit GUPTA

This article written by Akshit GUPTA (ESSEC Business School, Master in Management, 2019-2022) presents the subject of call-put parity.

Introduction

The call-put parity (also written the put-call parity) is a concept introduced in the 1960s by the economist Hans R. Stoll in a paper named “The Relationship Between Put and Call Option Prices”. The call-put parity shows the relationship between the prices of a put option, a call option, and the underlying asset. The call option and the put option are written on the same underlying asset and have the same expiration date and strike price. The call-put parity is applicable only on European options with a fixed time to expiration (it is not applicable to American options).

Call-put parity relation

The call-put parity relation is given by the equality:

Formula for the call put parity

Where t is the evaluation date (any date between the issuance date and the maturity date of the option), C_t the price of the call option, P_t the price of the put option, S_t the price of the underlying asset, K the strike price of the two options (same strike price for the call and put options), T the maturity date of the two options (same maturity date for the call and put options) and r the risk-free rate.

The call-put parity relation is sometimes written in different ways:

Formula for the call put parity styles

Demonstration

Let us try to find the call-put parity relation for a put option and a call option, which are European options with the same strike price K and the same maturity date T.

Let us consider a portfolio composed a long position in the underlying asset, a long position in the put option, a short position in the call option and a short position of a zero-coupon bond maturing at time T and of final value K.

Let us compute the value of this position at time T. The underlying asset is worth S_T. The zero-coupon bond is worth K. Regarding the call and put options, we can distinguish two cases: S_T > K and S_T < K.

In the first case, the put option finishes out of the money and the call finishes in the money and is worth S_T – K. The value of the position is then equal to: S_T + 0 – (S_T – K) – K, which is equal to zero.

In the second case, the call option finishes out of the money and the put finishes in the money and is worth K – S_T. The value of the position is then equal to: S_T + (K – S_T) – 0 – K, which is equal to zero.

If the value of the position at time T is also equal to 0, then the value of the position at time t is also equal to 0. If there is no arbitrage, then the value of the position by detailing its components satisfies:

Formula for the call put parity without arbitrage

which leads to the formula given above.

Application

The call-put parity formula helps the investors to calculate the price of a put option from the price of a call option, or inversely, to calculate the price of a call option from the price of a put option (the call option and the put option are written on the same underlying asset and have the same expiration date T and strike price K).

Implication

If the put-call parity does not hold true, there exists an arbitrage opportunity for investors. An arbitrage opportunity helps the investors earn profits without taking any risks. But the chances of finding an arbitrage opportunity is low given the high liquidity in the markets.

Example of application of the call-put parity

Assuming the stock of APPLE is trading at $25 in the market, the strike price of a 3-month European call option on Apple stock is $24 and the premium is $5. The risk-free rate is 8%.

Now, using the call-put parity,

Formula for the call put parity styles

we can calculate the price of the 3-month European put option on Apple stock with the same strike price, which is as follows:

The price of the call option (C) is $5, the price of the underlying asset (S) is $25, the present value of the strike price (K) is $23.52, and the risk-free rate (r) is 8% (market data).

As per the formula: P = $5 – $25 + $23.52, the price of the put option (P) is approximately equal to $3.52.

Useful resources

Academic research

Hull J.C. (2015) Options, Futures, and Other Derivatives, Ninth Edition, Chapter 11 – Properties of Stock Options, 256-275.

Stoll H.R. (1969) “The Relationship Between Put and Call Option Prices,” The Journal of Finance, 24(5): 801-824.

About the author

Article written in August 2021 by Akshit GUPTA (ESSEC Business School, Master in Management, 2019-2022).

Option Greeks – Theta

February 3, 2026August 19, 2021 by Akshit GUPTA

This article written by Akshit GUPTA (ESSEC Business School, Master in Management, 2019-2022) presents the technical subject of theta, an option Greek used in option pricing and hedging to deal with he passing of time.

Introduction

Theta is a type of option Greek which is used to compute the sensitivity or rate of change of the value of an option contract with respect to its time to maturity. The theta is denoted using the symbol (θ). Essentially, the theta is the first partial derivative of the price of the option contract with respect to the time to maturity of the option contract.

It is shown as:

Formula for the theta

Where V is the value of the option contract and T the time to maturity for the option contract.

Theoretically, as the option contract approaches maturity, the theta of on option contract increases and moves towards zero as the time value or the time value of the option decreases. This is referred to as “theta decay”.

For example, an option contract is trading at a premium of $10 and has a theta of -0.8. Thus, with theta decay, the option price will decrease to $9.2 after one day and further to $6 after five days.

The figure below represent the theta of a call option as a function of the time to maturity:

Figure 1. Theta of a call option as a function of time to maturity.

Source: computation by the author (Model: Black-Scholes-Merton).

Intrinsic and time value of an option contract

Essentially, the price of an option contract consists of two values namely, the intrinsic value and the time value (sometimes called extrinsic value). The intrinsic value in the price of an option contract is the real value or the fundamental value of an option based on the price of the underlying asset at a given point in time.

For example, a call option contract has a strike price of $10 and the underlying asset has a market price of $17. Theoretically, the buyer of a call option can execute the contract and buy the asset at $10 and sell it in the market for $17. He/she can make an immediate profit of $7 if they decide to exercise the option. Thus, the intrinsic value of the option contract is $7.

If the current call option price/premium is $9 in the market and the intrinsic value is $7, then the time value can be calculated as:

Time Value for the theta

Thus, the time value is $9-$7 is equal to $2. The $2 is the time value of an option contract which is determined by the factors other than the price of the underlying asset. As the option approaches maturity, the time value of the option contract declines and tends to zero. The price of an option contract which is at the money or out the money, it consists entirely of the time value as there is no intrinsic value involved.

For example, a call option contract with a strike price of $20, the underlying asset price of $15, and option premium of $3, has a time value equal to the option premium, $3, since the option is out of money.

Calculating Theta for call and put options

The theta for a non-dividend paying stock in a European call and put option is calculated using the following formula from the Black-Scholes Merton model:

Formula for the theta of a call and a put option

Where N’(d₁) represents the first order derivative of the cumulative distribution function of the normal distribution given by:

First_ derivative_Normal_distribution_d1

d₁ is given by:

Formula for d1

d₂ is given by:

Formula for d2

And N(-d₂) is given by:

Formula for -d2

Where S is the price of the underlying asset (at the time of valuation of the option), σ the volatility in the price of the underlying asset, T time to option’s maturity, K the strike price of the option contract and r the risk-free rate of return.

Excel pricer to calculate the theta of an option

You can download below an Excel file for an option pricer (based on the Black-Scholes-Merton or BSM model) which allows you to calculate the theta of a European-style call option.

Example for calculating theta

Let us consider a call option contract with the following characteristics: the underlying asset is an Apple stock, the option strike price (K) is equal to $300 and the time to maturity (T) is of one month (i.e., 0.084 years).

At the time of valuation, the price of the Apple stock (S) is $300, the volatility (σ) of Apple stock is 30% and the risk-free rate (r) is 3% (market data).

The theta of a call option is approximately equal to -0.2636 per trading day.

Using the above example, we can say that after one trading day, the price of the option will decrease by $0.2636 (approximately) due to time decay.

Useful resources

Hull J.C. (2015) Options, Futures, and Other Derivatives, Ninth Edition, Chapter 19 – The Greek Letters, 424–431.

Wilmott P. (2007) Paul Wilmott Introduces Quantitative Finance, Second Edition, Chapter 8 – The Black Scholes Formula and The Greeks, 182-184.

About the author

Article written in August 2021 by Akshit GUPTA (ESSEC Business School, Master in Management, 2019-2022).

Option Greeks – Vega

December 28, 2025August 19, 2021 by Akshit GUPTA

This article written by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) explains the technical subject of vega, the option Greek used in option pricing and hedging to take into account the volatility of the underlying asset.

Introduction

Vega is a type of option Greek which is used to compute the sensitivity or rate of change of the value of an option contract with respect to the volatility of the underlying asset. The Vega is denoted using the Greek letter (ν). Essentially, the vega is the first partial derivative of the value of the option contract with respect to the volatility of the underlying asset.

The vega formula for an option is given by

Formula for the gamma

Where V is the value of the option contract and σ is the volatility of the underlying asset.

If the Vega is a very high positive or a negative number, this means that the option price is highly sensitive to the volatility of the underlying asset. The Vega is maximum when the option price is at the money. For example, the strike of an option contract is €100, and the price of the underlying asset is €100. The option is at the money (ATM) and has an intrinsic value of zero. So, the option premium entirely consists of the time value of the option. Thus, the Vega is the highest for at the money option contract since the option value are mostly dependent on the time value (sometimes called the extrinsic value). An increase/decrease in volatility can change the option value significantly for at-the-money options.

Figure 1 below represents the vega of a call option as a function of the price of the underlying asset. The parameters of the call option are a maturity of 3 months and a strike of €100. The market data are a price of the underlying asset between €50 and €150, a volatility of the underlying asset of 40%, a risk-free interest rate of 3% and a dividend yield of 0%.

Figure 1. Vega of a call option as a function of the price of the underlying asset.

Source: computation by the author (Model: Black-Scholes-Merton).

Calculating the vega for call and put options

The vega for a European call or put option is calculated using the following formula:

Formula for the gamma

where

N’(d₁) represents the first order derivative of the cumulative distribution function of the normal distribution given by:

First_ derivative_Normal_distribution_d1

and d₁ is given by:

Formula for d1

where S is the price of the underlying asset (at the time of valuation of the option), σ the volatility in the price of the underlying asset, T time to option’s maturity, K the strike price of the option contract and r the risk-free rate of return.

Example for calculating vega

At the time of valuation, the price of the Apple stock (S) is $300, the volatility (σ) of Apple stock is 30% and the risk-free rate (r) is 3% (market data).

The vega of the call option is approximately equal to 0.3447963.

Using the above value, we can say that due to a 1% change in the volatility of the underlying asset, the price of the option will change approximately by $0.3447.

Excel pricer to calculate the vega of an option

You can download below an Excel pricer (based on the Black-Scholes-Merton or BSM model) to calculate the vega of an option (call or put).

Useful resources

Hull J.C. (2015) Options, Futures, and Other Derivatives, Ninth Edition, Chapter 19 – The Greek Letters, 424–431.

Wilmott P. (2007) Paul Wilmott Introduces Quantitative Finance, Second Edition, Chapter 8 – The Black Scholes Formula and The Greeks, 182-184.

About the author

Article written in August 2021 by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).

Option Greeks – Gamma

February 4, 2024August 8, 2021 by Akshit GUPTA

Option Greeks – Gamma

This article written by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) presents the technical subject of gamma, an option Greek used in option hedging.

Introduction

Gamma is a type of option Greek which is used to compute the sensitivity or rate of change of delta (Δ) of an option contract with respect to a change in the price of the underlying in the option contract (S). The gamma of an option is expressed in percentage terms. Denoted by the Greek letter (Γ), the gamma is defined by

Formula for the gamma of an option

Where (Δ) is the delta of the option and S the price of the underlying asset.

Essentially, the gamma is the second partial derivative of the value of the option contract (V) with respect to the price of the underlying asset (S). It measures the convexity of the value of the option contract with respect to the price of the underlying asset. The gamma then corresponds to

Formula for the gamma of an option

Where V is the value of the option and S the price of the underlying asset.

The gamma of an option contract is at its maximum when the price of the underlying asset is equal to the strike price of the option (an at-the-money option). If the price of the underlying moves deeper in the money or out of the money, the value of the gamma approaches zero.

The gamma as a function of the price of the underlying asset for a call option is given below.

Figure 1. Gamma of a call option.

Source: computation by the author (Model: Black-Scholes-Merton).

Also, if the gamma of the option contract is small, it means that the delta of the option moves slowly with the price of the underlying asset.

Calculating gamma for call and put options

The gamma for European call or put options on a non-dividend paying stock is calculated using the following formula from the Black-Scholes-Merton model is:

Formula for the gamma of a call/put option

Where,N’d₁ represents the first order derivative of the cumulative distribution function of the normal distribution given by:

First_ derivative_Normal_distribution_d1

and d₁ is given by:

Formula for d1.png

Excel pricer to calculate the gamma of an option

You can download below an Excel file for an option pricer (based on the Black-Scholes-Merton or BSM model) which allows you to calculate the gamma of a European-style call option.

Delta-gamma hedging

A trader holding a portfolio of option contracts uses gamma hedging to offset the risks associated with the price movement in the underlying asset by buying and selling the option contracts to maintain a constant delta. Generally, the delta is maintained near or at the zero level to attain delta neutrality. The neutrality in the gamma for the option is required to protect the portfolio’s value against sharp price movements in the price of the underlying asset.

Formula for the gamma hedging of a call option

Limitations of gamma hedging

The limitation of gamma hedging includes the following:

Transaction cost – Gamma hedging requires constantly monitoring the markets and buying or selling the option contracts. Due to this practice of buying and selling frequently, the transaction costs are quite high to execute a gamma hedge. Thus, gamma hedging is an expensive strategy to practice.
Loosing delta neutrality – Whenever a trader executes a gamma hedge and trades in option contracts, it is often accompanied with a move in the portfolio’s delta. Thus, to achieve delta neutrality again, the trader must buy or sell additional quantities of the underlying asset, which is time consuming and comes with a transaction cost.

Useful resources

Hull J.C. (2015) Options, Futures, and Other Derivatives, Ninth Edition, Chapter 19 – The Greek Letters, 424–431.

Wilmott P. (2007) Paul Wilmott Introduces Quantitative Finance, Second Edition, Chapter 8 – The Black Scholes Formula and The Greeks, 182-184.

About the author

Article written in August 2021 by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).

Option Greeks – Delta

January 27, 2026August 5, 2021 by Akshit GUPTA

This article written by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) presents the technical subject of delta, an option Greek used in option pricing and hedging.

Introduction

Option Greeks are sophisticated financial metric used by trader to calculate the sensitivity of option contracts to different factors related to the underlying asset including the price of the underlying, its volatility, and time value. The Greeks are used as an effective tool to practice different hedging strategies and eliminate risks in a position. They also help to optimize the options positions at any point in time.

Delta is a type of option Greek which is used to compute the sensitivity or rate of change in price of the option contract with respect to the change in price of the underlying asset. It is denoted by the Greek letter (Δ). The formula for calculating the delta of an option contract is:

Formula for the delta of an option

Where V is the value of the option and S the price of the underlying asset.

For example, if an option on Apple stock has a delta of 0.3, it essentially means that a $1 change in the price of the underlying asset i.e., Apple stock, will lead to a change of $0.3 in the price of the option contract.

When a trader takes a position based on the delta sensitivity of any option contract, it is called delta hedging. The goal is to achieve a delta-neutral portfolio and eliminate the risks associated with movement in the prices of the underlying. Due to the complexity of the tool, delta hedging is generally practiced by professional traders in large financial institutions. In options, the delta of any call option is always positive whereas the delta of a put option is always negative.

Delta formula

Call option

According the Black-Scholes-Merton model, the formula for calculating the delta for a European-style call option on a non-dividend paying stock is given by:

Formula for the delta of a call option

Where N represents the cumulative distribution function of the normal distribution and d₁ is given by:

Formula for d1

Where S is the price of the underlying asset (at the time of valuation of the option), σ the volatility in the price of the underlying asset, T time to maturity of the option, K the strike price of the option, and r the risk-free rate of return.

Put option

According the Black-Scholes-Merton model, the formula for calculating the delta for a European-style put option on a non-dividend paying stock is given by:

Formula for the delta of a put option

Delta as a function of the price of the underlying asset

Call option

The delta as a function of the price of the underlying asset for a European-style call option is represented in Figure 1.

Figure 1. Delta of a call option.

Source: computation by the author (Model: Black-Scholes-Merton).

For a call option, the delta increases from 0 (out-of-the-money option) to 1 (in-the-money option).

Put option

The delta as a function of the price of the underlying asset for a European-style put option is represented in Figure 2.

Figure 2. Delta of a put option.

Source: computation by the author (Model: Black-Scholes-Merton).

For a put option, the delta increases from -1 (in-the-money option) to 0 (out-of-the-money option).

Excel pricer to calculate the delta of an option

You can download below an Excel file for an option pricer (based on the Black-Scholes-Merton or BSM model) which allows you to calculate the delta of a European-style call option.

Delta Hedging

A trader holding an option contract uses delta hedging to offset the risks associated with the price movement in the underlying asset by continuously buying and selling the underlying asset to achieve delta neutrality. This is used by option traders in financial institutions to manage their option book (the delta is computed at the option level and aggregated at the book level) and generate the margin the bank of the option writing activity.

The delta of an option contract keeps on changing as the prices of the underlying and the option contract changes. So, to maintain the delta neutrality the trader must constantly monitor the markets and execute trades to achieve neutrality. The process of continuously buying or selling the underlying asset is called dynamic hedging in options.

At the first order, the change of the value of a delta-hedged call option over the period from t to t+ δt would be equal to the risk-free rate (r) over the period:

Formula for the delta hedging of a call option

Limitations of delta hedging

Although delta hedging is a useful tool to offset the risks associated to the movement in the price of an underlying, it comes with some limitations which are:

Transaction cost

Since delta hedging requires constantly buying or selling the underlying asset, it comes with a high transaction cost. This makes delta hedging an expensive tool to optimize the portfolio against price risk. In practice, traders would adjust their option position from time top time.

Illiquid Markets

When the market for an asset is illiquid, it is difficult to practice delta hedging as the trader will not be able to constantly buy or sell the underlying asset to neutralize the price impact.

Example for calculating delta

At the time of valuation, the price of the Apple stock (S) is $300, the volatility (σ) of Apple stock is 30% and the risk-free rate (r) is 3% (market data).

The delta of a call option is approximately equal to 0.50238.

Using the above value, we can say that due to a $1 change in the price of the underlying asset, the price of the option will change by $0.50238.

Useful resources

Research articles

Black F. and M. Scholes (1973) The Pricing of Options and Corporate Liabilities The Journal of Political Economy, 81, 637-654.

Merton R.C. (1973) Theory of Rational Option Pricing Bell Journal of Economics, 4(1): 141–183.

Books

Hull J.C. (2015) Options, Futures, and Other Derivatives, Ninth Edition, Chapter 19 – The Greek Letters, 424 – 431.

Wilmott P. (2007) Paul Wilmott Introduces Quantitative Finance, Second Edition, Chapter 8 – The Black Scholes Formula and The Greeks, 182-184.

About the author

Article written in August 2021 by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).

Understanding financial derivatives: options

August 2, 2021 by Alexandre VERLET

In this article, Alexandre VERLET (ESSEC Business School, Master in Management, 2017-2021) explains why financial markets invented options and how they function.

A historical perspective on options

The history of options is surrounded by legends.. This story is linked to human’s desire to control the unpredictable, sometimes to protect himself from it, often to profit from it. This story is also that of a flower: the tulip. At the beginning of the seventeenth century, in the Netherlands, the tulip was at the origin of the first known speculative bubble. Furthermore, this was historically the first time that options contracts were used on such a large scale. The possibility of profiting from the rise in the price of tulips by paying only a small part of the price aroused great interest on the part of speculators, thus increasing the price of the precious flower tenfold. Soon the price of the tulip reached levels completely unrelated to its market value. Then, suddenly, demand dried up, causing the price to fall even faster than the previous rise. The crisis that followed had serious consequences and confirmed Amsterdam’s loss of world leadership in finance to the benefit of London, which had already taken over the Dutch capital as the world’s center for international trade. Educated by the Dutch experience, the British became increasingly sceptical about options, so much so that they eventually banned them for over a century. The ban was finally lifted towards the end of the 19th century. It was also at this time that options were introduced in the United States.

The American options market entered a new dimension at the end of the 20th century. Indeed, 1973 was a pivotal year in the history of options in more ways than one. In March 1973, a floating exchange rate regime was adopted as the standard for converting international currencies, creating unprecedented instability in the currency market. This was also the year of the “first oil shock”. Also in 1973, the Chicago Board Options Exchange (CBOE), the first exchange entirely dedicated to options, opened its doors. The same year saw the birth of the Options Clearing Corporation (OCC), the first clearing house dedicated to options. Finally, 1973 saw the publication of the work of Fischer Black and Myron Scholes. This work was completed by Robert Merton, leading to the Black-Scholes-Merton model. This model is of capital importance for the evaluation of the price of options.

What’s an option?

There are two types of option contracts: calls and puts. Since these contracts can be both bought and sold, there are four basic transactions. Thus, in options trading, it is possible to either go long (buy a call contract, buy a put contract), or to be short (sell a call contract, sell a put contract). An option contract can therefore be defined as a contract that gives the counterparty buying the contract (the long) the right, but not the obligation, to buy or sell an asset (the underlying) at a predetermined price (the strike price), date (the maturity date) and amount (the nominal value). It is useful to note that the counterparty selling the contracts (the short) is in a completely different situation. This counterparty must sell or buy the underlying asset if the transaction is unfavorable to it. However, if the transaction is favorable, this counterparty will not receive any capital gain, because the counterparty buying the contract (the long) will not have exercised its call option. To compensate for the asymmetry of this transaction, the counterparty selling the option contracts (the short) will receive a premium at the time the contract is initiated. The selling counterparty therefore has a role similar to that of an insurance company, as it is certain to receive the premium, but has no control over the time of payment or the amount to be paid. This is why it is important to assess the amount of the premium.

The characteristic of an option contract

Options contracts can have as underlying assets financial assets (interest rates, currencies, stocks, etc.), physical assets (agricultural products, metals, energy sources, etc.), stock or weather indices, and even other derivatives (futures or forwards). The other important feature of an option contract is its expiration date. Options contracts generally have standardized expiry dates. Expiry dates can be monthly, quarterly or semi-annually. In most cases, the expiration date coincides with the third Friday of the expiration month. In addition, options whose only possible exercise date is the maturity date are called European options. However, when the option can be exercised at any time between signing and expiration, it is called an American option. Ultimately, what will drive the holder of an option contract to exercise his right is the difference between the underlying price and the strike price. The strike price is the purchase or sale price of the underlying asset. This price is chosen at the time the option contract is signed. The strike price will remain the same until the end of the option contract, unlike the price of the underlying asset, which will vary according to supply and demand. In organised markets, brokers usually offer the possibility to choose between several strike prices. The strike price can be identical to the price of the underlying asset. The option is then said to be “at-the-money” (or “at par”).

In the case of a call, if the proposed strike price is higher than the price of the underlying, the call is said to be “out of the money”.

Are you “in the money”?

Let’s take an example: a share is quoted at 10 euros. You are offered a call with a price of 11 euros. If we disregard the premium, we can see that a resale of the call, immediately after buying it, will result in a loss of one euro. For this reason, the call is said to be “out of the money”. On the other hand, when the strike price offered for a call is lower than the price of the underlying asset, the call is said to be “in the money”. Another example: the stock is still trading at 10 euros. This time you are offered a call with a strike price of 9 euros. If you disregard the premium, you can see that you earn one euro if you sell the call immediately after buying it. This is why this call is called “in the money”. Note that our potential gain of one euro is also called the “intrinsic value” of the call. Of course, the intrinsic value is only valid for “in the money” options. For puts, it is the opposite. A put is said to be “out of the money” if its strike price is lower than the price of the underlying asset.

Finally, a put is said to be “in the money” if its strike price is higher than the price of the underlying asset. If you are one of those people who think that you can make money with options by simply buying and selling calls or puts “in the money”, I have bad news for you! In reality, the premiums of the different contracts are calculated in such a way as to cancel out the advantage that “in the money” contracts offer over other contracts.

Useful resources

ISDA

About the author

Article written in July 2021 by Alexandre VERLET (ESSEC Business School, Master in Management, 2017-2021).

Options

January 18, 2026June 20, 2021 by Akshit GUPTA

This article written by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) presents an introduction to Options.

Introduction

Options is a type of derivative which gives the buyer of the option contract the right, but not the obligation, to buy (for a call option) or sell (for a put option) an underlying asset at a price which is pre-determined, and a date set in the future.

Option contracts can be traded between two or more counterparties either over the counter or on an exchange, where the contracts are listed. Exchange based trading of option contracts was introduced to the larger public in April 1973, when Chicago Board Options Exchange (CBOE)) was introduced in the US. The options market has grown ever since with over 50 exchanges that trade option contracts worldwide.

Terminology used for an option contract

The different terms that are used in an option contract are:

Option Spot price

The option spot price is the price at which the option contract is trading at the time of entering the contract.

Underlying spot price

The underlying spot price is the price at which the underlying asset is trading at the time of entering the option contract.

Strike price

Strike price is essentially the price at which the option buyer can exercise his/her right to buy or sell the option contract at or before the expiration date. The strike price is pre-determined at the time of entering the contract.

Expiration date

The expiration date is the date at which the option contracts ends or after which it becomes void. The expiration date of an option contract can be set to be after weeks, months or year.

Lot size

A lot size is the quantity of the underlying asset contained in an option contract. The size is decided and amended by the exchanges from time to time. For example, an Option contract on an APPLE stock trading on an exchange in USA consists of 100 underlying APPLE stocks.

Option class

Option class is the type of option contracts that the trader is trading on. It can be a Call or a Put option.

Position

The position a trader can hold in an option contract can either be Long or Short depending on the strategy. A Long position essentially means Buying the option and a short position means Selling or writing the option contract.

Option Premium

Option premium is the price at which the option contracts trade in the market.

Benefits of using an option contract

Trading in option contracts gives the traders certain benefits which can be categorised as:

Hedging Benefits

Hedging is an essential benefit of the option contract. For an investor or a trader holding an underlying stock, an option contract provides them with the opportunity to offset their risk exposure by buying or selling an option contract as per their market outlook. If an trader holding stocks of APPLE is bearish about the market and expects the market to fall, he/she can buy a PUT option which essentially gives him/her the right to sell the security at a pre-determined price and date. Such a contract protects the trader from significant losses which he/she might incur if the stock price for APPLE goes down significantly.

Cost Benefits

While buying an option contract, the traders benefits from the leverage effect which exchanges across the world provides. Leverage helps the traders to multiply the size of their holdings with lesser capital investment. This also helps them to earn higher profits by taking limited risks.

Choice Benefits

In traditional trading, traders have a limited degree of flexibility as they can only buy or sell assets based on their outlook. Whereas, Option contracts provides a great choice to the traders as they can take different positions in call and put options (Long and short positions) and for different strikes and maturities.
They can also use different strategies and spreads to execute and manage their positions to earn profits.

Types of option contracts

The option contracts can be broadly classified into two categories: call options and put options.

Call options

A call option is a derivative contract which gives the holder of the option the right, but not an obligation, to buy an underlying asset at a pre-determined price on a certain date. An investor buys a call option when he believes that the price of the underlying asset will increase in value in the future. The price at which the options trade in an exchange is called an option premium and the date on which an option contract expires is called the expiration date or the maturity date.

For example, an investor buys a call option on Apple shares which expires in 1 month and the strike price is $90. The current apple share price is $100. If after 1 month,
The share price of Apple is $110, the investor exercises his rights and buys the Apple shares from the call option seller at $90.

But, if the share prices for Apple falls to $80, the investor doesn’t exercise his right and the option expires because the investor can buy the Apple shares from the open market at $80.

Put options

A put option is a derivative contract which gives the holder of the option the right, but not an obligation, to sell an underlying asset at a pre-determined price on a certain date. An investor buys a put option when he believes that the price of the underlying asset will decrease in value in the future.

For example, an investor buys a put option on Apple shares which expires in 1 month and the strike price is $110. The current apple share price is $100. If after 1 month,
The share price of Apple is $90, the investor exercises his rights and sell the Apple shares to the put option seller at $110.
But, if the share prices for Apple rises to $120, the investor doesn’t exercise his right and the option expires because the investor can sell the Apple shares in the open market at $120.

Different styles of option exercise

The option style doesn’t deal with the geographical location of where they are traded. However, the contracts differ in terms of their expiration time when they can be exercised. The option contracts can be categorized as per different styles they come in. Some of the most common styles of option contracts are:

American options

American style options give the option buyer the right to exercise his option any time prior or up to the expiration date of the contract. These options provide greater flexibility to the option buyer but also comes at a high price as compared to the European style options.

European options

European style options can only be exercised on the expiration or maturity date of the contract. Thus, they offer less flexibility to the option buyer in terms of his rights. However, the European options are cheaper as compared to the American options.

Bermuda options

Bermuda options are a mix of both American and European style options. These options can only be exercised on a specific pre-determined dates up to the expiration date. They are considered to be exotic option contracts and provide limited flexibility to the option buyer to exercise his claim.

Different underlying assets for an option contract

The different underlying assets for an option contract can be:

Individual assets: stocks, bonds

Option traders trading in individual assets can take positions in call or put options for equities and bonds based on the reports provided by the research teams. They can take long or short positions in the option contract. The positions depend on the market trends and individual asset analysis. The option contracts on individual assets are traded in different lot sizes.

Indexes: stock indexes, bond indexes

Options traders can also trade on contracts based on different indexes. These contracts can be traded over the counter or on an exchange. These traders generally follow the macroeconomic trends of different geographies and trade in the indices based on specific markets or sectors. For example, some of the most known exchange traded index options are options written on the CAC 40 index in France, the S&P 500 index and the Dow Jones Industrial Average Index in the US, etc.

Foreign currency options

Different banks and investment firms deal in currency hedges to mitigate the risk associated with cross border transactions. Options traders at these firms trade in foreign currency option contracts, which can be over the counter or exchange traded.

Option Positions

Option traders can take different positions depending on the type of option contract they trade. The positions can include:

Long Call

When a trader has a long position in a call option it essentially means that he has bought the call option which gives the trader the right to buy the underlying asset at a pre-determined price and date. The buyer of the call option pays a price to the option seller to buy the right and the price is called the Option Premium. The maximum loss to a call option buyer is restricted to the amount of the option premium he/she pays.

Long Call

With the following notations:
C_T = Call option value at maturity T
S_T = Price of the underlying at maturity T
K = Strike price of the call option

The graph of the payoff of a long call is depicted below. It gives the value of the long position in a call option at maturity T as a function of the price of the underlying asset at time T.

Payoff of a long position in a call option
Long call

Short Call

When a trader has a short position in a call option it essentially means that he has sold the call option which gives the buyer of the option the right to buy the underlying asset from the seller at a pre-determined price and date. The seller of the call option is also called the option writer and he/she receive a price from the option buyer called the Option Premium. The maximum gain to a call option seller is restricted to the amount of the option premium he/she receives.

Short call

With the following notations:
C_T = Call option value at maturity T
S_T = Price of the underlying at maturity T
K = Strike price of the call option

The graph of the payoff of a short call is depicted below. It gives the value of the short position in a call option at maturity T as a function of the price of the underlying asset at time T.

Payoff of a short position in a call option
Short call

Long Put

When a trader has a long position in a put option it essentially means that he/she has bought the put option which gives the trader the right to sell the underlying asset at a pre-determined price and date. The buyer of the put option pays a price to the option seller to buy the right and the price is called the Option Premium. The maximum loss to a put option buyer is restricted to the amount of the option premium he/she pays.

Long Put

With the following notations:
P_T = Put option value at maturity T
S_T = Price of the underlying at maturity T
K = Strike price of the put option

The graph of the payoff of a long put is depicted below. It gives the value of the long position in a put option at maturity T as a function of the price of the underlying asset at time T.

Payoff of a long position in a put option
Long put

Short Put

When a trader has a short position in a put option it essentially means that he has sold the call option which gives the buyer of the option the right to sell the underlying asset from the seller at a pre-determined price and date. The seller of the put option is also called the option writer and he/she receive a price from the option buyer called the Option Premium. The maximum gain to a put option seller is restricted to the amount of the option premium he/she receives.

Short Put

With the following notations:
P_T = Put option value at maturity T
S_T = Price of the underlying at maturity T
K = Strike price of the put option

The graph of the payoff of a short put is depicted below. It gives the value of the short position in a put option at maturity T as a function of the price of the underlying asset at time T.

Payoff of a short position in a put option
Short put

Useful Resources

Academic research

Hull J.C. (2015) Options, Futures, and Other Derivatives, Ninth Edition, Chapter 10 – Mechanics of options markets, 235-240.

Business analysis

CNBC Live option trading for APPLE stocks

About the author

Article written in June 2021 by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).

History of Options Markets

December 18, 2025June 20, 2021 by Akshit GUPTA

This article written by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) presents an introduction to the History of the Options markets.

Introduction

Options are a type of derivative contracts which give the buyer the right, but not the obligation, to buy or sell an underlying security at a pre-determined price and date. These contracts can either be traded over-the-counter (OTC) through dealer or broker network or can be traded over an exchange in a standardized form.

A brief history

The history of the use of options can be dated back to ancient times. In early 4th century BC, a philosopher, and an astronomer, named Thales of Miletus calculated a surplus olive harvest in his region during the period. He predicted an increase in demand for the olive presses due to an increase in the harvest. To benefit from his prediction, he bought the rights to use the olive presses in his region by paying a certain sum. The olive harvest saw a significant surplus that year and the demand for olive presses rose, as predicted by him. He then exercised his option and sold the rights to use the olive presses at a much higher prices than what he actually paid, making a good profit. This is the first documented account of the use of option contracts dating back to 4th century BC.

The use of option contracts was also seen during the Tulip mania of 1636. The tulip producers used to sell call options to the investors when the tulip bulbs were planted. The investors had the right to buy the tulips, when they were ready for harvest, at a price pre-determined while buying the call option. However, since the markets were highly unstandardized, the producers could default on their obligations.
But the event laid a strong foundation for the use of option contracts in the future.

Until 1970s, option contracts were traded over-the-counter (OTC) between investors. However, these contracts were highly unstandardized leading to investor distrust and illiquidity in the market.

In 1973, the Chicago Board Options Exchange (CBOE)) was formed in USA, laying the first standardized foundation in options trading. In 1975, the Options clearing corporation (OCC) was formed to act as a central clearing house for all the option contracts that were traded on the exchange. With the introduction of these 2 important bodies, the option trading became highly standardized and general public gained access to it. However, the Put options were introduced only in 1977 by CBOE. Prior to that, only Call options were traded on the exchange.

With the advent of time, options market grew significantly with more exchanges opening up across the world. The option pricing models, and risk management strategies also became more sophisticated and complex.

Market participants

The participants in the options markets can be broadly classified into following groups:

Market makers: A market maker is a market participant in the financial markets that simultaneously buys and sells quantities of any option contract by posting limit orders. The market maker posts limit orders in the market and profits from the bid-ask spread, which is the difference by which the ask price exceeds the bid price. They play a significant role in the market by providing liquidity.
Margin traders: Margin traders are market participants who make use of the leverage factor to invest in the options markets and increase their position size to earn significant profits. But this trading style is highly speculative and can also lead to high losses due to the leverage effect.
Hedgers: Investors who try to reduce their exposure in the financial markets by using hedging strategies are called hedgers. Hedgers often trades in derivative products to offset their risk exposure in the underlying assets. For example, a hedger who is bearish about the market and has shares of Apple, will buy a Put option on the shares of Apple. Thus, he has the right to sell the shares at a high price if the market price for apple shares goes down.
Speculators: Speculative investors are involved in option trading to take advantage of market movements. They usually speculative on the price of an underlying asset and account for a significant share in option trading.

Types of option contracts

The option contracts can be broadly classified into two main categories, namely:

Call options

But, if the share prices for Apple falls to $80, the investor doesn’t exercise his right and the option expires because the investor can buy the Apple shares from the open market at $80.

Put options

For example, an investor buys a put option on Apple shares which expires in 1 month and the strike price is $110. The current apple share price is $100. If after 1 month,

The share price of Apple is $90, the investor exercises his rights and sell the Apple shares to the put option seller at $110.

But, if the share prices for Apple rises to $120, the investor doesn’t exercise his right and the option expires because the investor can sell the Apple shares in the open market at $120.

Different style of options

American options

European options

Bermuda options

Useful Resources

Chapter 10 – Mechanics of options markets, pg. 235-240, Options, Futures, and Other Derivatives by John C. Hull, Ninth Edition

Wikipedia Options (Finance)

The Street A Brief History of Stock Options

About the author

Article written in June 2021 by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).

Plain Vanilla Options

Introduction

Types of options

Call options

Put options

Types of exercise

American options

European options

Bermudan options

Moneyness

In-the-money options

Out-of-the-money options

At-the-money options

Option writers

Benefits

Option Trading

Option pricing

Use of options

Hedging

Speculation

Volatility

Related posts on the SimTrade blog

Useful Resources

About the author

Derivatives Market

Introduction

Main types of derivative contracts

Forwards and Futures

Options

Swaps

Exchange-traded vs Over-the-counter Derivatives Market

Exchange-traded derivatives markets

Over-the-counter markets

Types of market participants

Hedgers

Speculators

Arbitrageurs

Margin Traders

Criticism of derivatives

Conclusion

Related posts on the SimTrade blog

Useful resources

About the author

The Black-Scholes-Merton model

Introduction

History

Option pricing with BSM

The BSM formula

Example – Call and Put option pricing using Black-Scholes-Merton model

Conclusion

Limitations of the BSM model

Related posts on the SimTrade blog

Useful resources

Academic research

About the author

Introduction

Call-put parity relation

Demonstration

Application

Implication

Example of application of the call-put parity

Related posts on the SimTrade blog

Useful resources

Academic research

About the author

Introduction

Intrinsic and time value of an option contract

Calculating Theta for call and put options

Excel pricer to calculate the theta of an option

Example for calculating theta

Related Posts on the SimTrade blog

Useful resources

About the author

Introduction

Calculating the vega for call and put options

Example for calculating vega

Excel pricer to calculate the vega of an option

Related posts ont he SimTrade blog

Option pricing and Greeks

Useful resources