Option Greeks – Gamma
This article written by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) presents the technical subject of gamma, an option Greek used in option hedging.
Introduction
Gamma is a type of option Greek which is used to compute the sensitivity or rate of change of delta (Δ) of an option contract with respect to a change in the price of the underlying in the option contract (S). The gamma of an option is expressed in percentage terms. Denoted by the Greek letter (Γ), the gamma is defined by
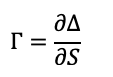
Where (Δ) is the delta of the option and S the price of the underlying asset.
Essentially, the gamma is the second partial derivative of the value of the option contract (V) with respect to the price of the underlying asset (S). It measures the convexity of the value of the option contract with respect to the price of the underlying asset. The gamma then corresponds to
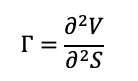
Where V is the value of the option and S the price of the underlying asset.
The gamma of an option contract is at its maximum when the price of the underlying asset is equal to the strike price of the option (an at-the-money option). If the price of the underlying moves deeper in the money or out of the money, the value of the gamma approaches zero.
The gamma as a function of the price of the underlying asset for a call option is given below.
Figure 1. Gamma of a call option.
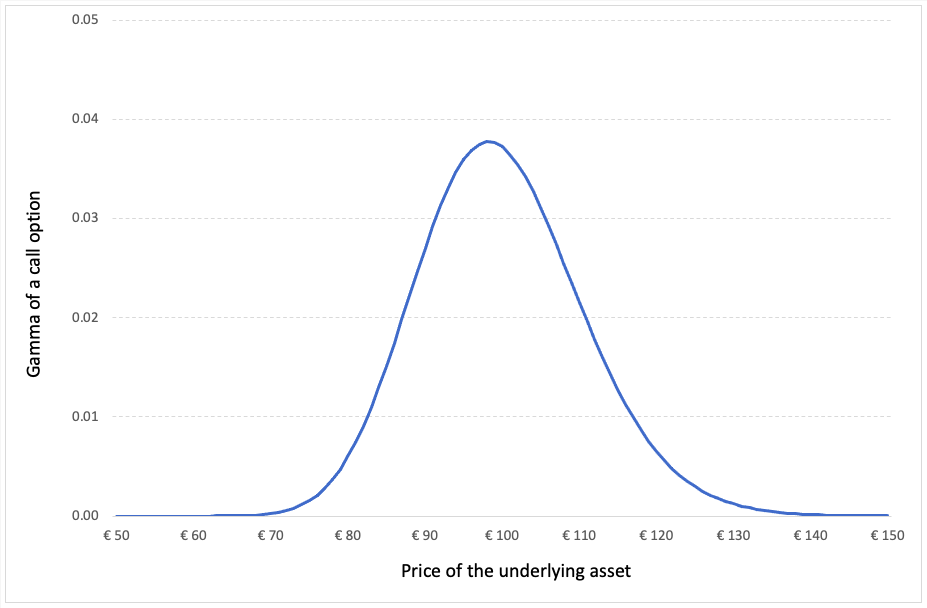
Source: computation by the author (Model: Black-Scholes-Merton).
Also, if the gamma of the option contract is small, it means that the delta of the option moves slowly with the price of the underlying asset.
Calculating gamma for call and put options
The gamma for European call or put options on a non-dividend paying stock is calculated using the following formula from the Black-Scholes-Merton model is:
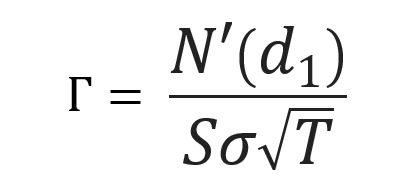
Where,N’d1 represents the first order derivative of the cumulative distribution function of the normal distribution given by:
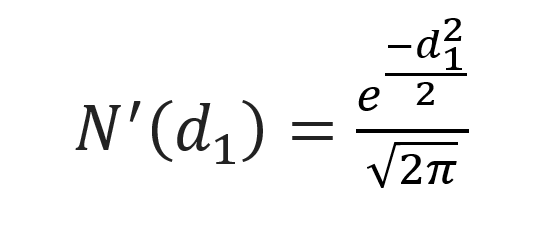
and d1 is given by:
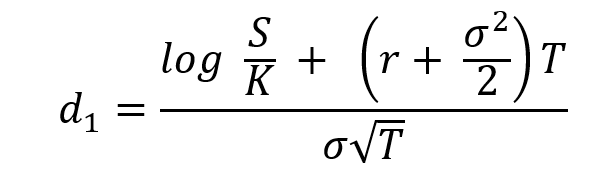
Where S is the price of the underlying asset (at the time of valuation of the option), σ the volatility in the price of the underlying asset, T time to option’s maturity, K the strike price of the option contract and r the risk-free rate of return.
Excel pricer to calculate the gamma of an option
You can download below an Excel file for an option pricer (based on the Black-Scholes-Merton or BSM model) which allows you to calculate the gamma of a European-style call option.
Delta-gamma hedging
A trader holding a portfolio of option contracts uses gamma hedging to offset the risks associated with the price movement in the underlying asset by buying and selling the option contracts to maintain a constant delta. Generally, the delta is maintained near or at the zero level to attain delta neutrality. The neutrality in the gamma for the option is required to protect the portfolio’s value against sharp price movements in the price of the underlying asset.
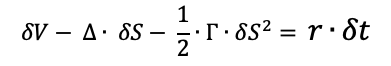
Limitations of gamma hedging
The limitation of gamma hedging includes the following:
- Transaction cost – Gamma hedging requires constantly monitoring the markets and buying or selling the option contracts. Due to this practice of buying and selling frequently, the transaction costs are quite high to execute a gamma hedge. Thus, gamma hedging is an expensive strategy to practice.
- Loosing delta neutrality – Whenever a trader executes a gamma hedge and trades in option contracts, it is often accompanied with a move in the portfolio’s delta. Thus, to achieve delta neutrality again, the trader must buy or sell additional quantities of the underlying asset, which is time consuming and comes with a transaction cost.
Related posts in the SimTrade blog
▶ Akshit GUPTA History of Options markets
▶ Akshit GUPTA Option Trader – Job description
▶ Jayati WALIA Black-Scholes-Merton option pricing model
▶ Akshit GUPTA Option Greeks – Delta
▶ Akshit GUPTA Option Greeks – Theta
▶ Akshit GUPTA Option Greeks – Vega
Useful resources
Hull J.C. (2015) Options, Futures, and Other Derivatives, Ninth Edition, Chapter 19 – The Greek Letters, 424–431.
Wilmott P. (2007) Paul Wilmott Introduces Quantitative Finance, Second Edition, Chapter 8 – The Black Scholes Formula and The Greeks, 182-184.
About the author
Article written in August 2021 by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).


