Option Greeks – Vega
This article written by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) explains the technical subject of vega, the option Greek used in option pricing and hedging to take into account the volatility of the underlying asset.
Introduction
Vega is a type of option Greek which is used to compute the sensitivity or rate of change of the value of an option contract with respect to the volatility of the underlying asset. The Vega is denoted using the Greek letter (ν). Essentially, the vega is the first partial derivative of the value of the option contract with respect to the volatility of the underlying asset.
The vega formula for an option is given by
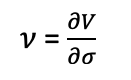
Where V is the value of the option contract and σ is the volatility of the underlying asset.
If the Vega is a very high positive or a negative number, this means that the option price is highly sensitive to the volatility of the underlying asset. The Vega is maximum when the option price is at the money. For example, the strike of an option contract is €100, and the price of the underlying asset is €100. The option is at the money (ATM) and has an intrinsic value of zero. So, the option premium entirely consists of the time value of the option. Thus, the Vega is the highest for at the money option contract since the option value are mostly dependent on the time value (sometimes called the extrinsic value). An increase/decrease in volatility can change the option value significantly for at-the-money options.
Figure 1 below represents the vega of a call option as a function of the price of the underlying asset. The parameters of the call option are a maturity of 3 months and a strike of €100. The market data are a price of the underlying asset between €50 and €150, a volatility of the underlying asset of 40%, a risk-free interest rate of 3% and a dividend yield of 0%.
Figure 1. Vega of a call option as a function of the price of the underlying asset.
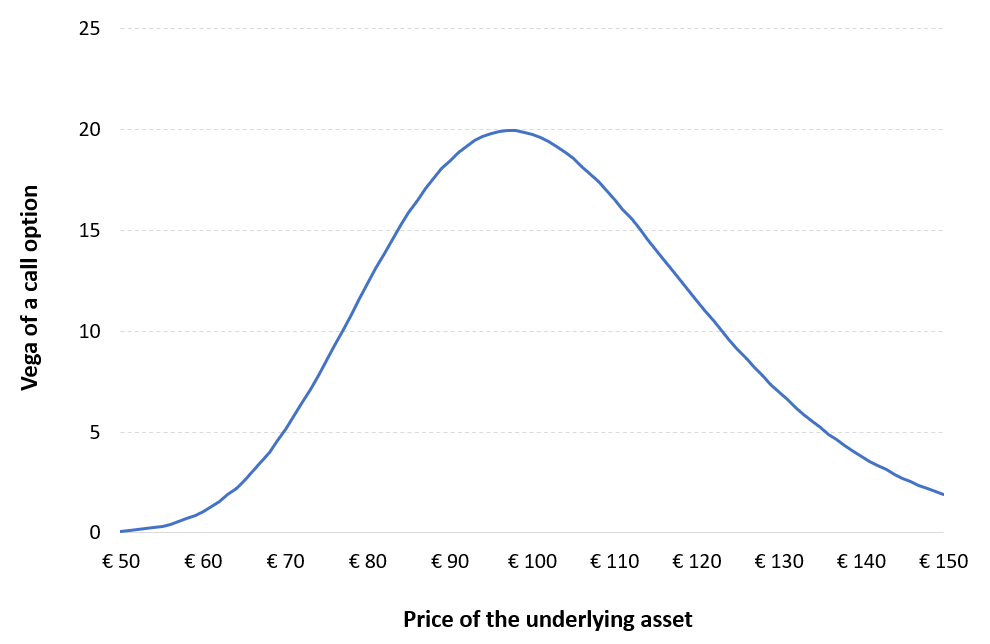
Source: computation by the author (Model: Black-Scholes-Merton).
Calculating the vega for call and put options
The vega for a European call or put option is calculated using the following formula:
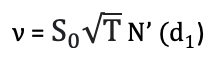
where
N’(d1) represents the first order derivative of the cumulative distribution function of the normal distribution given by:
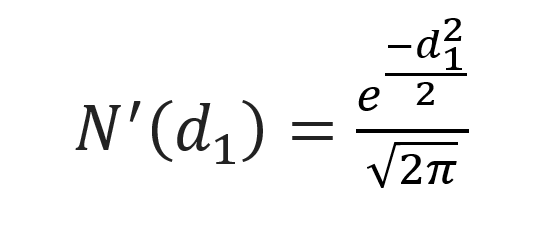
and d1 is given by:
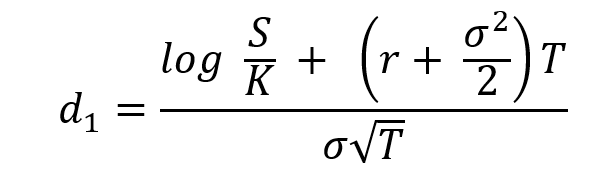
where S is the price of the underlying asset (at the time of valuation of the option), σ the volatility in the price of the underlying asset, T time to option’s maturity, K the strike price of the option contract and r the risk-free rate of return.
Example for calculating vega
Let us consider a call option contract with the following characteristics: the underlying asset is an Apple stock, the option strike price (K) is equal to $300 and the time to maturity (T) is of one month (i.e. 0.084 years).
At the time of valuation, the price of the Apple stock (S) is $300, the volatility (σ) of Apple stock is 30% and the risk-free rate (r) is 3% (market data).
The vega of the call option is approximately equal to 0.3447963.
Using the above value, we can say that due to a 1% change in the volatility of the underlying asset, the price of the option will change approximately by $0.3447.
Excel pricer to calculate the vega of an option
You can download below an Excel pricer (based on the Black-Scholes-Merton or BSM model) to calculate the vega of an option (call or put).
Related posts ont he SimTrade blog
▶ Akshit GUPTA Options
▶ Akshit GUPTA History of Options markets
▶ Akshit GUPTA Option Trader – Job description
Option pricing and Greeks
▶ Jayati WALIA Black-Scholes-Merton option pricing model
▶ Akshit GUPTA Option Greeks – Delta
▶ Akshit GUPTA Option Greeks – Gamma
▶ Akshit GUPTA Option Greeks – Theta
Useful resources
Hull J.C. (2015) Options, Futures, and Other Derivatives, Ninth Edition, Chapter 19 – The Greek Letters, 424–431.
Wilmott P. (2007) Paul Wilmott Introduces Quantitative Finance, Second Edition, Chapter 8 – The Black Scholes Formula and The Greeks, 182-184.
About the author
Article written in August 2021 by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).


