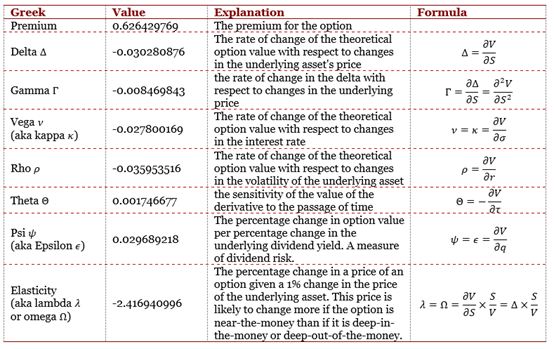
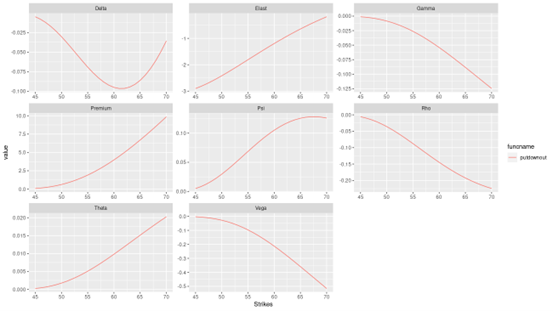
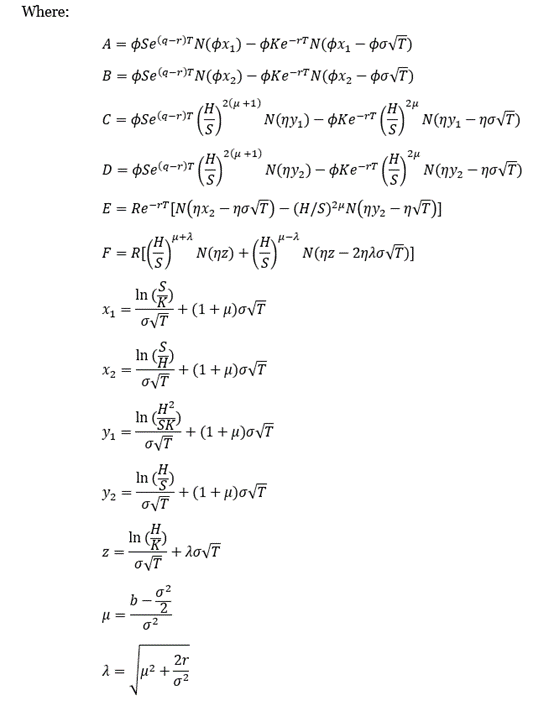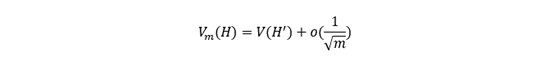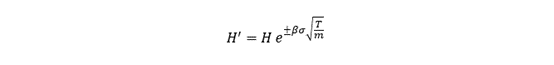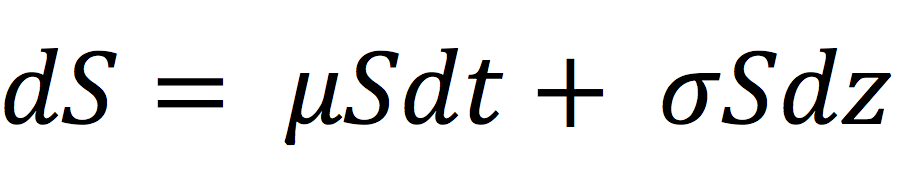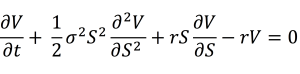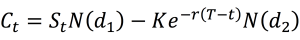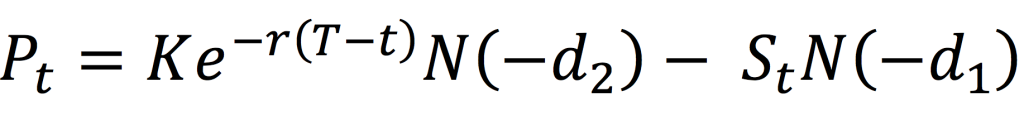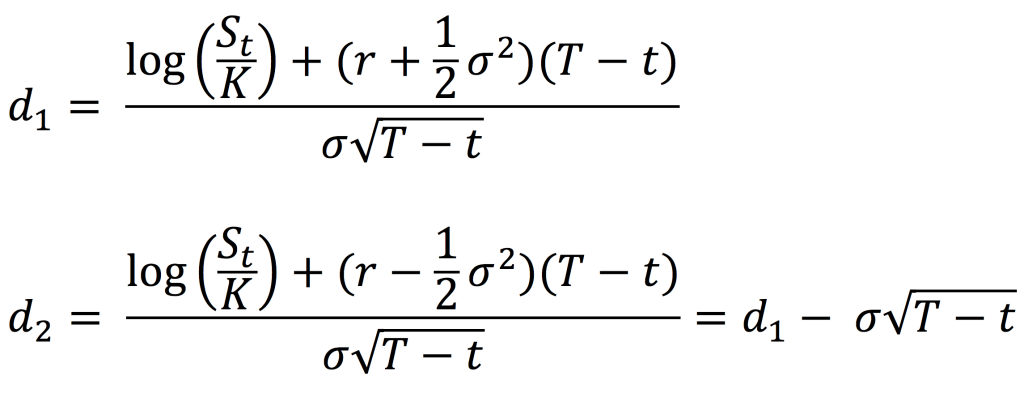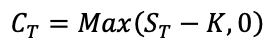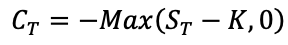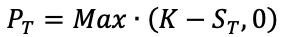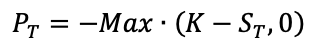Option pricing

Pricing barrier options with simulations and sensitivity analysis with Greeks

by

Pricing barrier options with simulations and sensitivity analysis with Greeks

Shengyu ZHENG

In this article, Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2023) explains the pricing of barrier options with Monte-Carlo simulations and the sensitivity analysis of barrier options from the perspective of Greeks.

Pricing of discretely monitored barrier options with Monte-Carlo simulations

With the simulation method, only the pricing of discretely monitored barrier options can be handled since it is impossible to simulate continuous price trajectories with no intervals. Here the method is illustrated with a down-and-out put option. The general setup of economic details of the down-and-out put option and related market information are presented as follows:

General setup of simulation for barrier option pricing

Similar to the simulation method for pricing standard vanilla options, Monte Carlo simulations based on Geometric Brownian Motion could also be employed to analyze the pricing of barrier options.

Figure 1. Trajectories of 600 price simulations.

With the R script presented above, we can simulate 6,000 times with the simprice() function from the derivmkts package. Trajectories of 600 price simulations are presented above, with the black line representing the mean of the final prices, the green dashed lines 1x and 2x standard deviation above the mean, the red dashed lines 1x and 2x derivation below the mean, the blue dashed line the strike level and the brown line the knock-out level.

The simprice() function, according to the documentation, computes simulated lognormal price paths with the given parameters.

With this simulation of 6,000 price paths, we arrive at a price of 0.6720201, which is quite close to the one calculated from the formulaic approach from the previous post.

Analysis of Greeks

The Greeks are the measures representing the sensitivity of the price of derivative products including options to a change in parameters such as the price and the volatility of the underlying asset, the risk-free interest rate, the passage of time, etc. Greeks are important elements to look at for risk management and hedging purposes, especially for market makers (dealers) since they do not essentially take these risks for themselves.

In R, with the combination of the greeks() function and a barrier pricing function, putdownout() in this case, we can easily arrive at the Greeks for this option.

Barrier option R code Sensitivity Greeks

Table 1. Greeks of the Down-and-Out Put

Barrier Option Greeks Summary

We can also have a look at the evolutions of the Greeks with the change of one of the parameters. The following R script presents an example of the evolutions of the Greeks along with the changes in the strike price of the down-and-out put option.

Barrier option R code Sensitivity Greeks Evolution

Figure 2. Evolution of Greeks with the change of Strike Price of a Down-and-Out Put

Evolution Greeks Barrier Price

Download R file to price barrier options

You can find below an R file (file with txt format) to price barrier options.

Download R file to price barrier options

Why should I be interested in this post?

As one of the most traded but the simplest exotic derivative products, barrier options open an avenue for different applications. They are also very often incorporated in structured products, such as reverse convertibles. It is, therefore, important to be equipped with knowledge of this product and to understand the pricing logics if one aspires to work in the domain of market finance.

Simulation methods are very common in pricing derivative products, especially for those without closed-formed pricing formulas. This post only presents a simple example of pricing barrier options and much optimization is needed for pricing more complex products with more rounds of simulations.

Related posts on the SimTrade blog

   ▶ All posts about Options

   ▶ Shengyu ZHENG Barrier options

   ▶ Shengyu ZHENG Pricing barrier options with analytical formulas

Useful resources

Academic articles

Broadie, M., Glasserman P., Kou S. (1997) A Continuity Correction for Discrete Barrier Option. Mathematical Finance, 7:325-349.

Merton, R. (1973) Theory of Rational Option Pricing. The Bell Journal of Economics and Management Science, 4:141-183.

Paixao, T. (2012) A Guide to Structured Products – Reverse Convertible on S&P500

Reiner, E.S., Rubinstein, M. (1991) Breaking down the barriers. Risk Magazine, 4(8), 28–35.

Rich, D. R. (1994) The Mathematical Foundations of Barrier Option-Pricing Theory. Advances in Futures and Options Research: A Research Annual, 7:267-311.

Wang, B., Wang, L. (2011) Pricing Barrier Options using Monte Carlo Methods, Working paper.

Books

Haug, E. (1997) The Complete Guide to Option Pricing. London/New York: McGraw-Hill.

Hull, J. (2006) Options, Futures, and Other Derivatives. Upper Saddle River, N.J: Pearson/Prentice Hall.

About the author

The article was written in June 2022 by Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2023).

Pricing barrier options with analytical formulas

by

Pricing barrier options with analytical formulas

Shengyu ZHENG

As is mentioned in the previous post, the frequency of monitoring is one of the determinants of the price of a barrier option. The higher the frequency, the more likely a barrier event would take place.

In this article, Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2023) explains the pricing of continuously and discretely monitored barrier options with analytical formulas.

Pricing of standard continuously monitored barrier options

For pricing standard barrier options, we cannot simply apply the Black-Sholes-Merton Formula for the particularity of the barrier conditions. There are, however, several models available developed on top of this theoretical basis. Among them, models developed by Merton (1973), Reiner and Rubinstein (1991) and Rich (1994) enabled the pricing of continuously monitored barrier options to be conducted in a formulaic fashion. They are concisely put together by Haug (1997) as follows:

Knock-in and knock-out barrier option pricing formula

Knock-in barrier option pricing formula

Knock-in barrier option pricing formula

Pricing of standard discretely monitored barrier options

For discretely monitored barrier options, Broadie and Glasserman (1997) derived an adjustment that is applicable on top of the pricing formulas of the continuously monitored counterparts.

Let’s denote:

Knock-in barrier option pricing formula

The price of a discretely monitored barrier option of a certain barrier price equals the price of a continuously monitored barrier option of the adjusted price plus an error:

Knock-in barrier option pricing formula

The adjusted barrier price, in this case, would be:

Knock-in barrier option pricing formula

Knock-in barrier option pricing formula

It is also worth noting that the error term o(·) grows prominently when the barrier approaches the strike price. A threshold of 5% from the strike price should be imposed if this approach is employed for pricing discretely monitored barrier options.

Example of pricing a down-and-out put with R with the formulaic approach

The general setup of economic details of the Down-and-Out Put and related market information is presented as follows:

Knock-in barrier option pricing formula

There are built-in functions in the “derivmkts” library that render directly the prices of barrier options of continuous monitoring, such as calldownin(), callupin(), calldownout(), callupout(), putdownin(), putupin(), putdownout(), and putupout (). By incorporating the adjustment proposed by Broadie and Glasserman (1997), all barrier options of both monitoring methods could be priced in a formulaic way with the following function:

Knock-in barrier option pricing formula

For example, for a down-and-out Put option with the aforementioned parameters, we can use this function to calculate the prices.

Knock-in barrier option pricing formula

For continuous monitoring, we get a price of 0.6264298, and for daily discrete monitoring, we get a price of 0.676141. It makes sense that for a down-and-out put option, a lower frequency of barrier monitoring means less probability of a knock-out event, thus less protection for the seller from extreme downside price trajectories. Therefore, the seller would charge a higher premium for this put option.

Download R file to price barrier options

You can find below an R file (file with txt format) to price barrier options.

Download R file to price barrier options

Why should I be interested in this post?

As one of the most traded but the simplest exotic derivative products, barrier options open an avenue for different applications. They are also very often incorporated in structured products, such as reverse convertibles. It is, therefore, important to understand the elements having an impact on their prices and the closed-form pricing formulas are a good presentation of these elements.

Related posts on the SimTrade blog

   ▶ All posts about options

   ▶ Shengyu ZHENG Barrier options

   ▶ Shengyu ZHENG Pricing barrier options with simulations and sensitivity analysis with Greeks

Useful resources

Academic research articles

Broadie, M., Glasserman P., Kou S. (1997) A Continuity Correction for Discrete Barrier Option. Mathematical Finance, 7:325-349.

Merton, R. (1973) Theory of Rational Option Pricing. The Bell Journal of Economics and Management Science, 4:141-183.

Paixao, T. (2012) A Guide to Structured Products – Reverse Convertible on S&P500

Reiner, E.S., Rubinstein, M. (1991) Breaking down the barriers. Risk Magazine, 4(8), 28–35.

Rich, D. R. (1994) The Mathematical Foundations of Barrier Option-Pricing Theory. Advances in Futures and Options Research: A Research Annual, 7:267-311.

Wang, B., Wang, L. (2011) Pricing Barrier Options using Monte Carlo Methods, Working paper.

Books

Haug, E. (1997) The Complete Guide to Option Pricing. London/New York: McGraw-Hill.

Hull, J. (2006) Options, Futures, and Other Derivatives. Upper Saddle River, N.J: Pearson/Prentice Hall.

About the author

The article was written in July 2022 by Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2023).

Black-Scholes-Merton option pricing model

by

Jayati WALIA

In this article, Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) explains the Black-Scholes-Merton model to price options.

The Black-Scholes-Merton model (or the BSM model) is the world’s most popular option pricing model. Developed in the beginning of the 1970s, this model introduced to the world, a mathematical way of pricing options. Its success was essentially a starting point for new forms of financial derivatives in the knowledge that they could be priced accurately using the ideas and analyses pioneered by Black, Scholes and Merton and it set the foundation for the flourishing of modern quantitative finance. Myron Scholes and Robert Merton were awarded the Nobel Prize for their work on option pricing in 1997. Unfortunately, Fischer Black had died several years earlier but would certainly have been included in the prize had he been alive, and he was also listed as a contributor by Scholes and Merton.

Today, the Black-Scholes-Merton formula is widely used by traders in investment banks to price and hedge option contracts. Options are used by investors to hedge their portfolios to manage their risks.

Assumptions of the BSM Model

As any model, the BSM model relies on a set of assumptions:

  • The model considers European options, which we can only be exercised at their expiration date.
  • The price of the underlying asset follows a geometric Brownian motion (corresponding to log-normal distribution for the price at a given point in time).
  • The risk-free rate remains constant over time until the expiration date.
  • The volatility of the underlying asset price remains constant over time until the expiration date.
  • There are no dividend payments on the underlying asset.
  • There are no transaction costs on the underlying asset.
  • There are no arbitrage opportunities.

The BSM equation

The value of an option is a function of the price of the underlying stock and its statistical behavior over the life of the option.

A commonly used model is Geometric Brownian Motion (GBM). GBM assumes that future asset price differences are uncorrelated over time and the probability distribution function of the future prices is a log-normal distribution (or equivalently the probability distribution function of the future returns is a normal distribution). The price movements in a GBM process can be expressed as:

GBM equation

with dS being the change in the underlying asset price in continuous time dt and dX the random variable from the normal distribution (N(0, 1) or Wiener process). σ is the volatility of the underlying asset price (it is assumed to be constant). μdt represents the deterministic return within the time interval with μ representing the growth rate of asset price or the ‘drift’.

Therefore, option price is determined by these parameters that describe the process followed by the asset price over a period of time. The Black-Scholes-Merton equation governs the price evolution of European stock options in financial markets. It is a linear parabolic partial differential equation (PDE) and is expressed as:

BSM model equation

Where V is the value of the option (as a function of two variables: the price of the underlying asset S and time t), r is the risk-free interest rate (think of it as the interest rate which you would receive from a government debt or similar debt securities) and σ is the volatility of the log returns of the underlying security (say stocks).

The key idea behind the equation is to hedge the option and limit exposure to market risk posed by the asset. This is achieved by a strategy known as ‘delta hedging’ and it involves replicating the option through an equivalent portfolio with positions in the underlying asset and a risk-free asset in the right way so as to eliminate risk.

Thus, from the BSM equation we can derive the BSM formulae that describe the price of call and put options over their life time.

The BSM formulae

Note that the type of option we are valuing (call or put), the strike price and the maturity date do not appear in the above BSM equation. These elements only appear in the ‘final condition’ i.e., the option value at maturity, called the payoff function.

For a call option, the payoff C is given by:

CT = max⁡(ST – K; 0)

For a put option, the payoff is given by:

PT = max⁡(K – ST; 0)

The BSM formula is a solution to the BSM equation, given the boundary conditions (given by the payoff equations above). It calculates the price at time t for both a call and a put option.

The value for a call option at time t is given by:

Call option value equation

The value for a put option at time t is given by:

Put option value equation

where

With the notations:
St: Price of the underlying asset at time t
t: Current date
T: Expiry date of the option
K: Strike price of the option
r: Risk-free interest rate
σ: Volatility (the standard deviation of the return on the underlying asset)
N(.): Cumulative distribution function for a normal (Gaussian) distribution. It is the probability that a random variable is less or equal to its input (i.e. d₁ and d₂) for a normal distribution. Thus, 0 ≤ N(.) ≤ 1

Figure 1 gives the graphical representation of the value of a call option at time t as a function of the price of the underlying asset at time t as given by the BSM formula. The strike price for the call option is 50€ with a maturity of 0.25 years and volatility of 50% in the underlying.

Figure 1. Call option value
Call option value
Source: computation by author.

Figure 2 gives the graphical representation of the value of a put option at time t as a function of the price of the underlying asset at time t as given by the BSM formula. The strike price for the put option is 50€ with a maturity of 0.25 years and volatility of 50% in the underlying.

Figure 2. Put option valuePut option value
Source: computation by author.

You can download below the Excel file for option pricing with the BSM Model.

Download the Excel file for option pricing with the BSM Model

Some Criticisms and Limitations

American options

The Black-Scholes-Merton model was initially developed for European options. This is a limitation of the equation for American options which can be exercised at any time before the expiry date. The BSM model would then not accurately determine the option value (an important case when the underlying asset pays a discrete dividend).

Stocks paying dividends

Also, in reality, most stocks pay dividends, and no dividends was an assumption in the initial BSM model, which analysts now eliminated by accommodating the dividend yield in the formula if required.

Constant volatility

Another limitation is the use of constant volatility. Volatility is the measure of risk based on the standard deviation of the return on the underlying asset. In reality the value of an asset will change randomly, not with a specific constant pattern regarding the way it can change.

Finally, the assumption of no transaction cost neglects the liquidity risk in the market since transaction costs are clearly incurred in the real world and there exists a bid-offer spread on most underlying assets. For the most heavily traded stocks, this cost may be low but for others it may lead to an inaccuracy.

Related posts on the SimTrade blog

▶ All posts about Options

▶ Jayati WALIA Brownian Motion in Finance

▶ Akshit GUPTA Options

▶ Akshit GUPTA The Black-Scholes-Merton model

▶ Akshit GUPTA History of options market

Useful resources

Black F. and M. Scholes (1973) The Pricing of Options and Corporate Liabilities The Journal of Political Economy 81, 637-654.

Merton R.C. (1973) Theory of Rational Option Pricing Bell Journal of Economics 4, 141–183.

About the author

The article was written in March 2022 by Jayati WALIA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).

Options

by

Options

Akshit GUPTA

This article written by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) presents an introduction to Options.

Introduction

Options is a type of derivative which gives the buyer of the option contract the right, but not the obligation, to buy (for a call option) or sell (for a put option) an underlying asset at a price which is pre-determined, and a date set in the future.

Option contracts can be traded between two or more counterparties either over the counter or on an exchange, where the contracts are listed. Exchange based trading of option contracts was introduced to the larger public in April 1973, when Chicago Board Options Exchange (CBOE)) was introduced in the US. The options market has grown ever since with over 50 exchanges that trade option contracts worldwide.

Terminology used for an option contract

The different terms that are used in an option contract are:

Option Spot price

The option spot price is the price at which the option contract is trading at the time of entering the contract.

Underlying spot price

The underlying spot price is the price at which the underlying asset is trading at the time of entering the option contract.

Strike price

Strike price is essentially the price at which the option buyer can exercise his/her right to buy or sell the option contract at or before the expiration date. The strike price is pre-determined at the time of entering the contract.

Expiration date

The expiration date is the date at which the option contracts ends or after which it becomes void. The expiration date of an option contract can be set to be after weeks, months or year.

Lot size

A lot size is the quantity of the underlying asset contained in an option contract. The size is decided and amended by the exchanges from time to time. For example, an Option contract on an APPLE stock trading on an exchange in USA consists of 100 underlying APPLE stocks.

Option class

Option class is the type of option contracts that the trader is trading on. It can be a Call or a Put option.

Position

The position a trader can hold in an option contract can either be Long or Short depending on the strategy. A Long position essentially means Buying the option and a short position means Selling or writing the option contract.

Option Premium

Option premium is the price at which the option contracts trade in the market.

Benefits of using an option contract

Trading in option contracts gives the traders certain benefits which can be categorised as:

Hedging Benefits

Hedging is an essential benefit of the option contract. For an investor or a trader holding an underlying stock, an option contract provides them with the opportunity to offset their risk exposure by buying or selling an option contract as per their market outlook. If an trader holding stocks of APPLE is bearish about the market and expects the market to fall, he/she can buy a PUT option which essentially gives him/her the right to sell the security at a pre-determined price and date. Such a contract protects the trader from significant losses which he/she might incur if the stock price for APPLE goes down significantly.

Cost Benefits

While buying an option contract, the traders benefits from the leverage effect which exchanges across the world provides. Leverage helps the traders to multiply the size of their holdings with lesser capital investment. This also helps them to earn higher profits by taking limited risks.

Choice Benefits

In traditional trading, traders have a limited degree of flexibility as they can only buy or sell assets based on their outlook. Whereas, Option contracts provides a great choice to the traders as they can take different positions in call and put options (Long and short positions) and for different strikes and maturities.
They can also use different strategies and spreads to execute and manage their positions to earn profits.

Types of option contracts

The option contracts can be broadly classified into two categories: call options and put options.

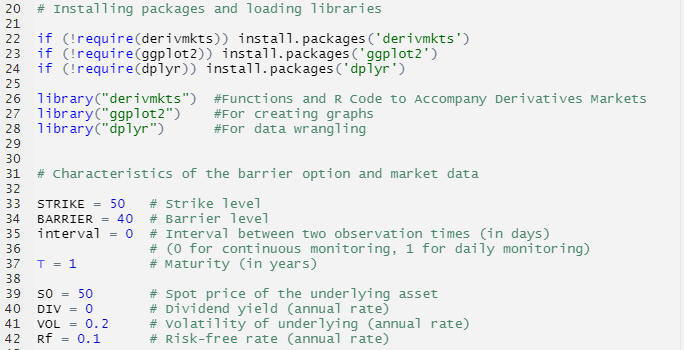
Call options

A call option is a derivative contract which gives the holder of the option the right, but not an obligation, to buy an underlying asset at a pre-determined price on a certain date. An investor buys a call option when he believes that the price of the underlying asset will increase in value in the future. The price at which the options trade in an exchange is called an option premium and the date on which an option contract expires is called the expiration date or the maturity date.

For example, an investor buys a call option on Apple shares which expires in 1 month and the strike price is $90. The current apple share price is $100. If after 1 month,
The share price of Apple is $110, the investor exercises his rights and buys the Apple shares from the call option seller at $90.

But, if the share prices for Apple falls to $80, the investor doesn’t exercise his right and the option expires because the investor can buy the Apple shares from the open market at $80.

Put options

A put option is a derivative contract which gives the holder of the option the right, but not an obligation, to sell an underlying asset at a pre-determined price on a certain date. An investor buys a put option when he believes that the price of the underlying asset will decrease in value in the future.

For example, an investor buys a put option on Apple shares which expires in 1 month and the strike price is $110. The current apple share price is $100. If after 1 month,
The share price of Apple is $90, the investor exercises his rights and sell the Apple shares to the put option seller at $110.
But, if the share prices for Apple rises to $120, the investor doesn’t exercise his right and the option expires because the investor can sell the Apple shares in the open market at $120.

Different styles of option exercise

The option style doesn’t deal with the geographical location of where they are traded. However, the contracts differ in terms of their expiration time when they can be exercised. The option contracts can be categorized as per different styles they come in. Some of the most common styles of option contracts are:

American options

American style options give the option buyer the right to exercise his option any time prior or up to the expiration date of the contract. These options provide greater flexibility to the option buyer but also comes at a high price as compared to the European style options.

European options

European style options can only be exercised on the expiration or maturity date of the contract. Thus, they offer less flexibility to the option buyer in terms of his rights. However, the European options are cheaper as compared to the American options.

Bermuda options

Bermuda options are a mix of both American and European style options. These options can only be exercised on a specific pre-determined dates up to the expiration date. They are considered to be exotic option contracts and provide limited flexibility to the option buyer to exercise his claim.

Different underlying assets for an option contract

The different underlying assets for an option contract can be:

Individual assets: stocks, bonds

Option traders trading in individual assets can take positions in call or put options for equities and bonds based on the reports provided by the research teams. They can take long or short positions in the option contract. The positions depend on the market trends and individual asset analysis. The option contracts on individual assets are traded in different lot sizes.

Indexes: stock indexes, bond indexes

Options traders can also trade on contracts based on different indexes. These contracts can be traded over the counter or on an exchange. These traders generally follow the macroeconomic trends of different geographies and trade in the indices based on specific markets or sectors. For example, some of the most known exchange traded index options are options written on the CAC 40 index in France, the S&P 500 index and the Dow Jones Industrial Average Index in the US, etc.

Foreign currency options

Different banks and investment firms deal in currency hedges to mitigate the risk associated with cross border transactions. Options traders at these firms trade in foreign currency option contracts, which can be over the counter or exchange traded.

Option Positions

Option traders can take different positions depending on the type of option contract they trade. The positions can include:

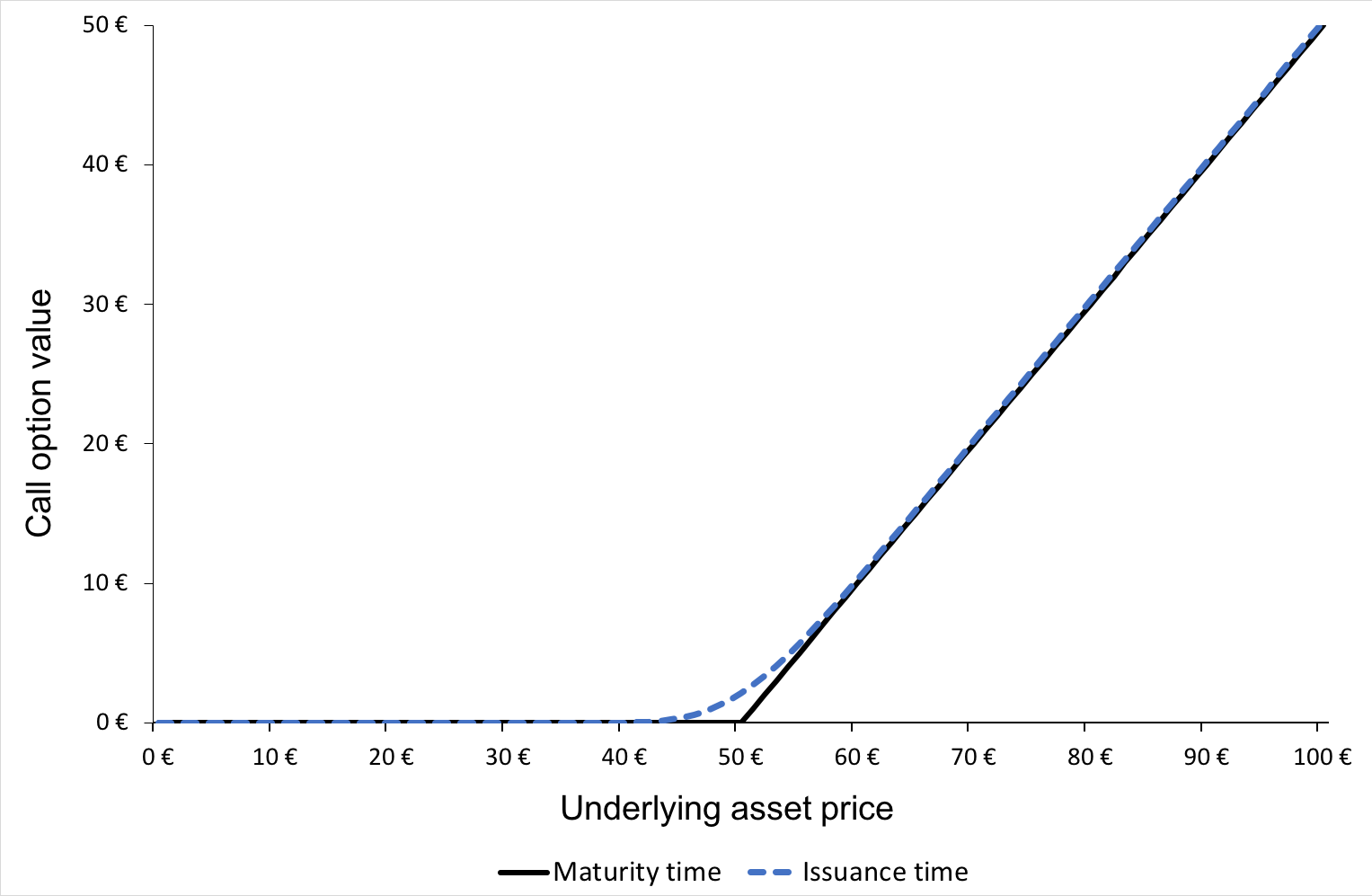
Long Call

When a trader has a long position in a call option it essentially means that he has bought the call option which gives the trader the right to buy the underlying asset at a pre-determined price and date. The buyer of the call option pays a price to the option seller to buy the right and the price is called the Option Premium. The maximum loss to a call option buyer is restricted to the amount of the option premium he/she pays.

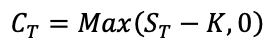
Long Call

With the following notations:
   CT = Call option value at maturity T
   ST = Price of the underlying at maturity T
   K = Strike price of the call option

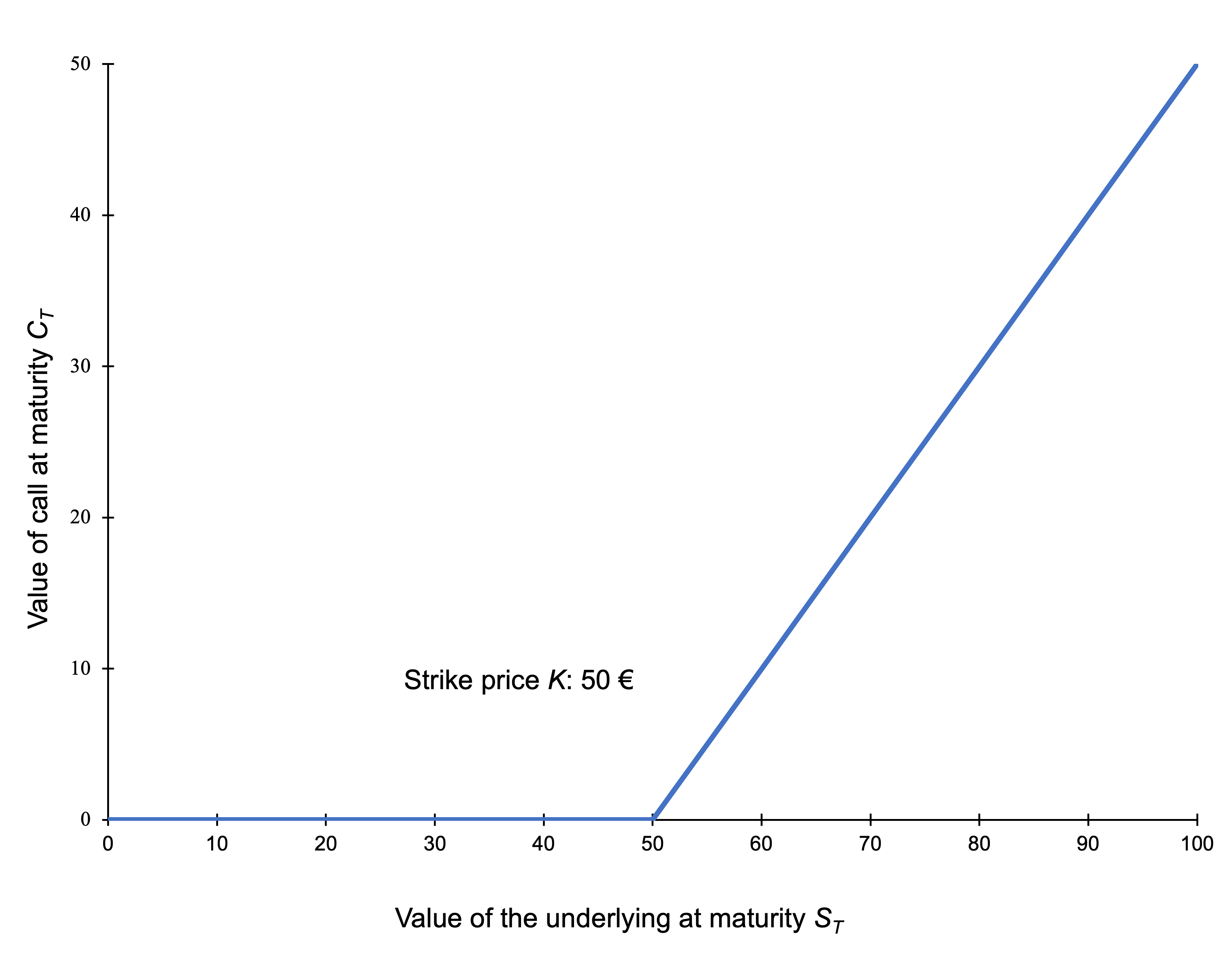
The graph of the payoff of a long call is depicted below. It gives the value of the long position in a call option at maturity T as a function of the price of the underlying asset at time T.

Payoff of a long position in a call option
Long call

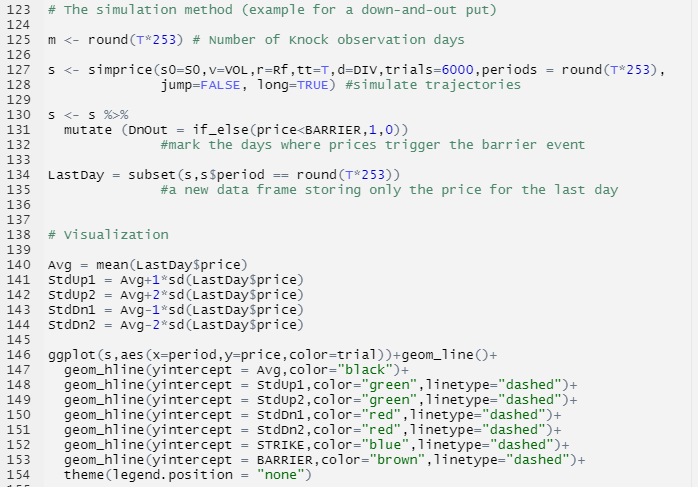
Short Call

When a trader has a short position in a call option it essentially means that he has sold the call option which gives the buyer of the option the right to buy the underlying asset from the seller at a pre-determined price and date. The seller of the call option is also called the option writer and he/she receive a price from the option buyer called the Option Premium. The maximum gain to a call option seller is restricted to the amount of the option premium he/she receives.

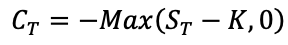
Short call

With the following notations:
   CT = Call option value at maturity T
   ST = Price of the underlying at maturity T
   K = Strike price of the call option

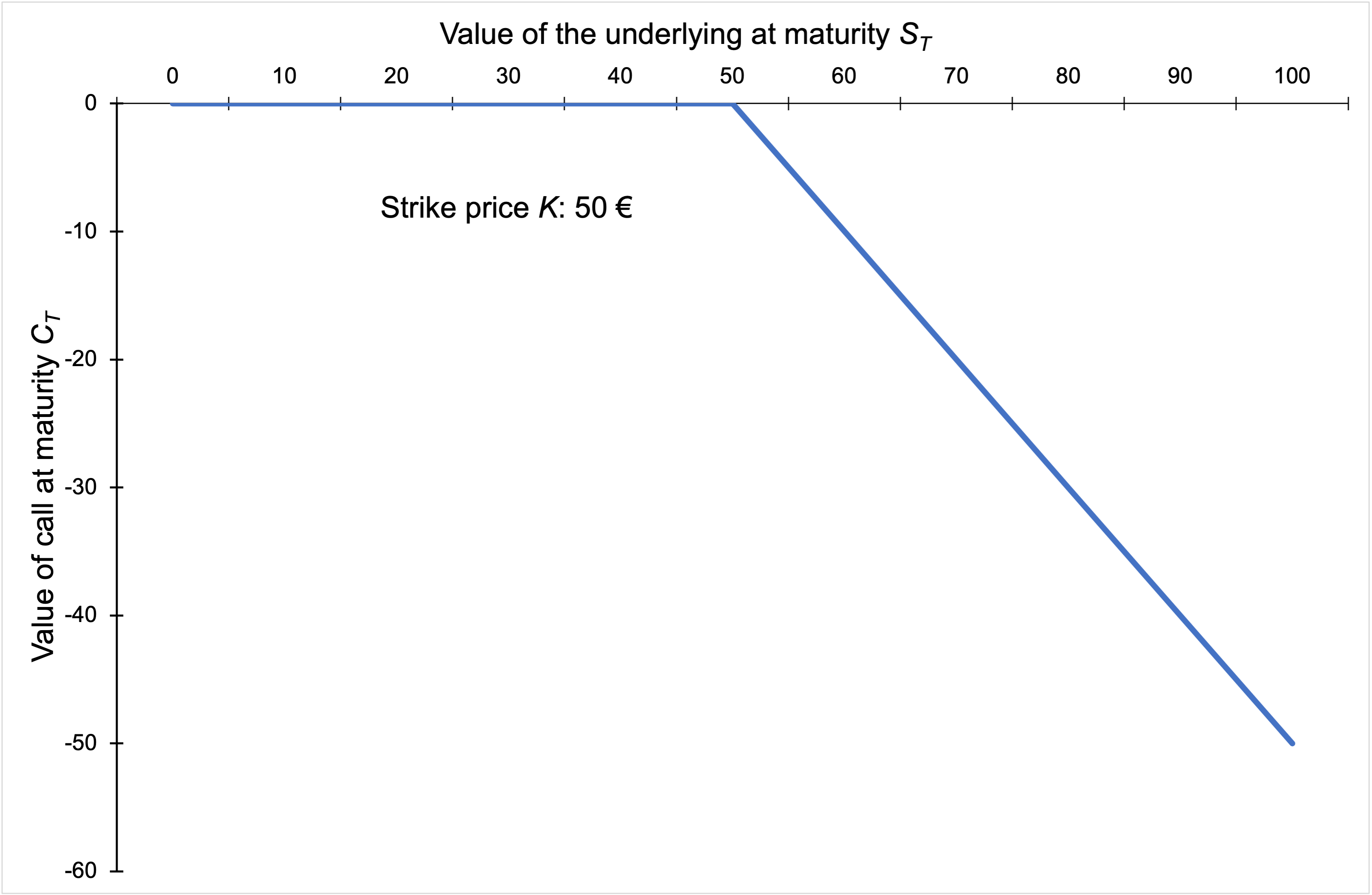
The graph of the payoff of a short call is depicted below. It gives the value of the short position in a call option at maturity T as a function of the price of the underlying asset at time T.

Payoff of a short position in a call option
Short call

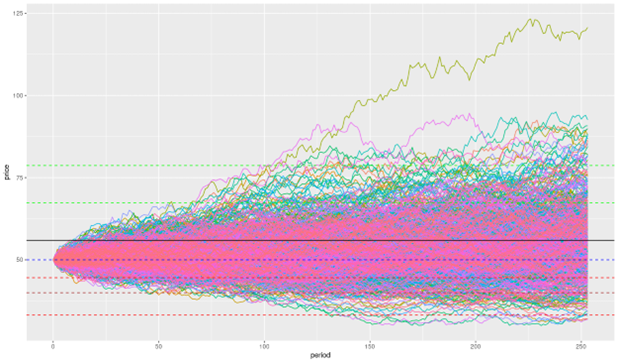
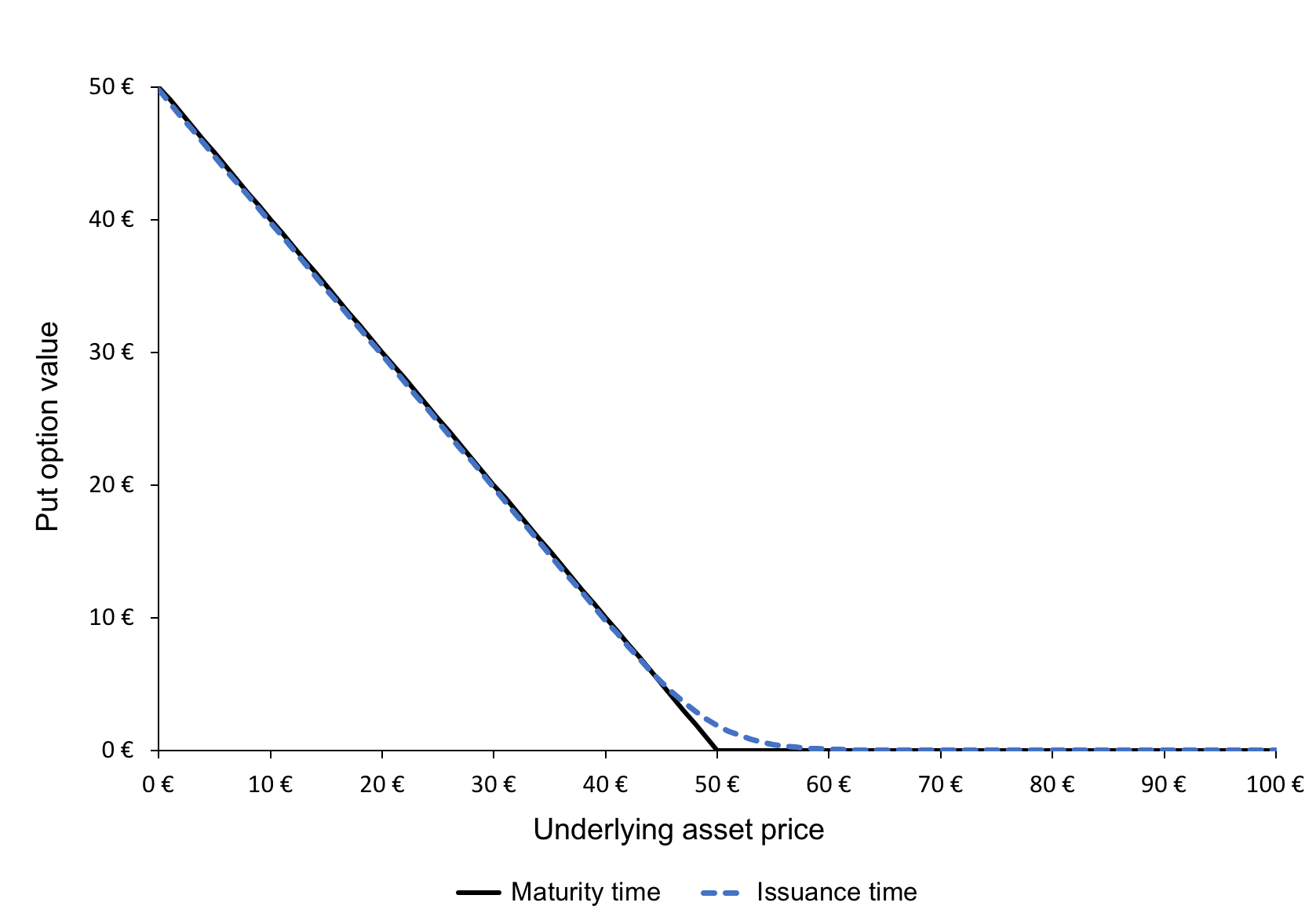
Long Put

When a trader has a long position in a put option it essentially means that he/she has bought the put option which gives the trader the right to sell the underlying asset at a pre-determined price and date. The buyer of the put option pays a price to the option seller to buy the right and the price is called the Option Premium. The maximum loss to a put option buyer is restricted to the amount of the option premium he/she pays.

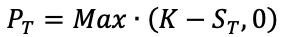
Long Put

With the following notations:
   PT = Put option value at maturity T
   ST = Price of the underlying at maturity T
   K = Strike price of the put option

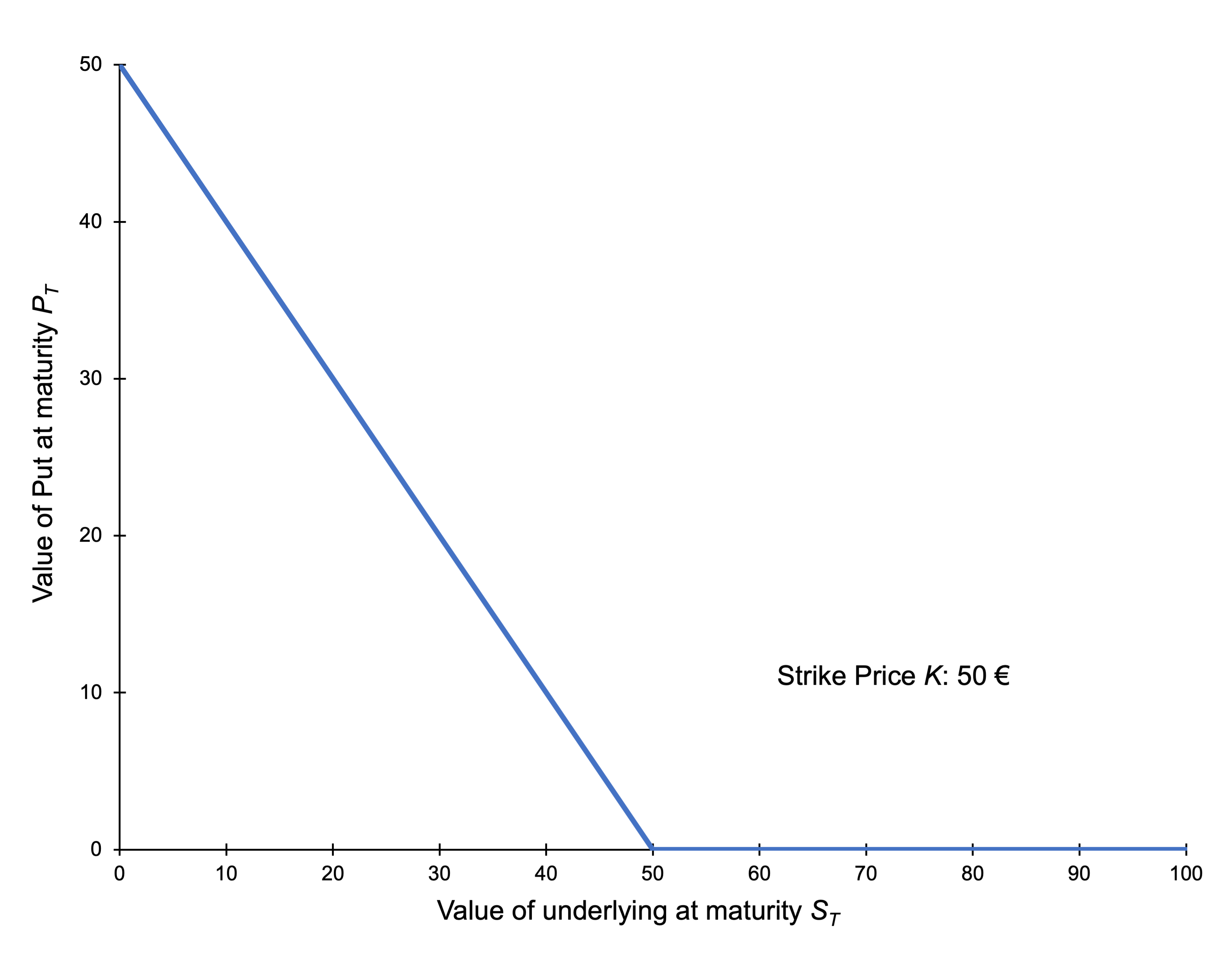
The graph of the payoff of a long put is depicted below. It gives the value of the long position in a put option at maturity T as a function of the price of the underlying asset at time T.

Payoff of a long position in a put option
Long put

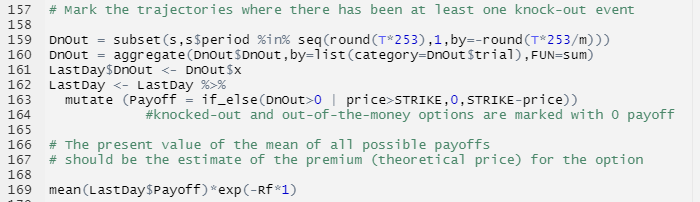
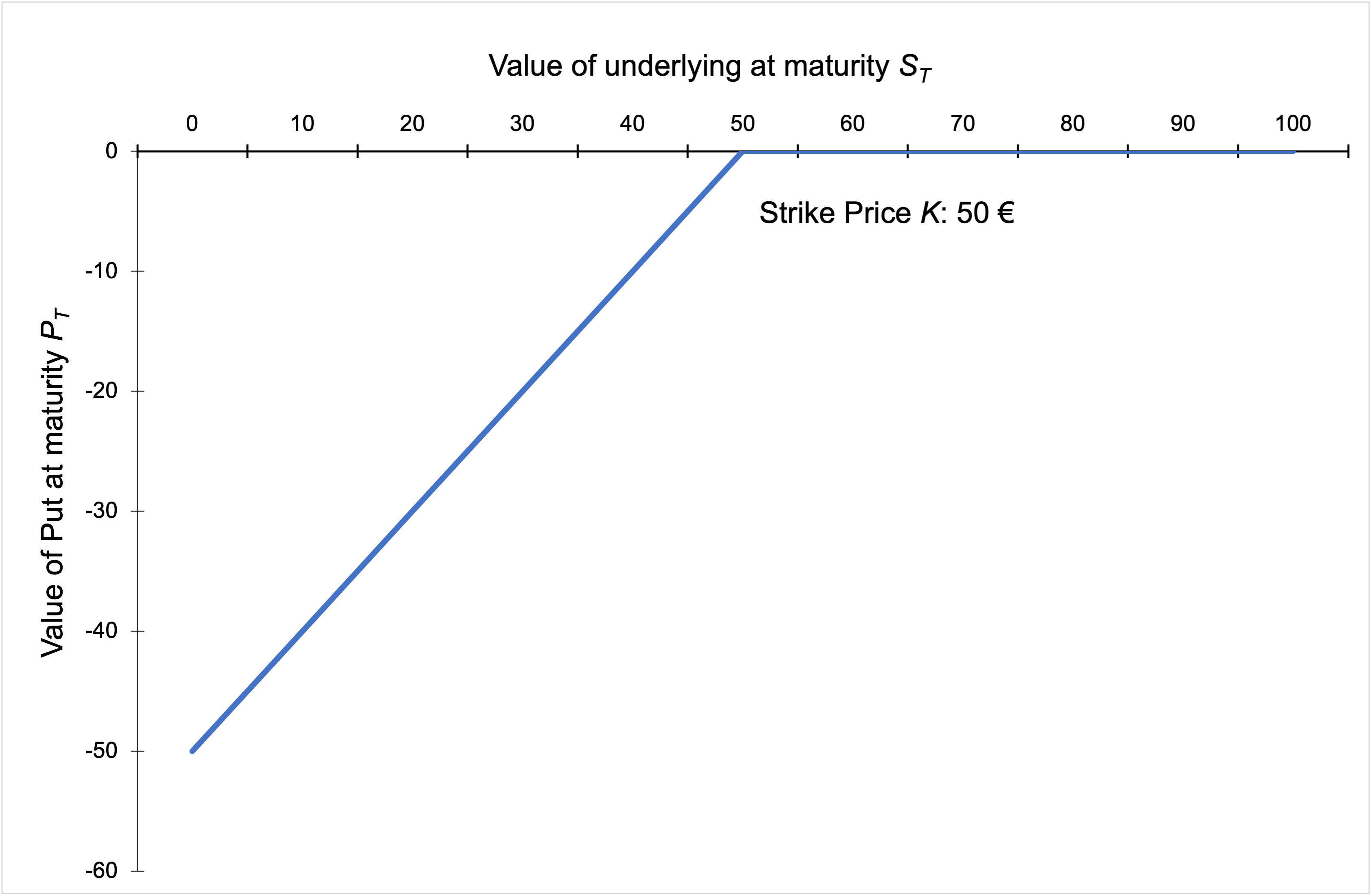
Short Put

When a trader has a short position in a put option it essentially means that he has sold the call option which gives the buyer of the option the right to sell the underlying asset from the seller at a pre-determined price and date. The seller of the put option is also called the option writer and he/she receive a price from the option buyer called the Option Premium. The maximum gain to a put option seller is restricted to the amount of the option premium he/she receives.

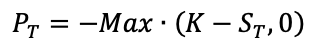
Short Put

With the following notations:
   PT = Put option value at maturity T
   ST = Price of the underlying at maturity T
   K = Strike price of the put option

The graph of the payoff of a short put is depicted below. It gives the value of the short position in a put option at maturity T as a function of the price of the underlying asset at time T.

Payoff of a short position in a put option
Short put

Related posts on the SimTrade blog

   ▶ All posts about Options

   ▶ Jayati WALIA Black-Scholes-Merton option pricing model

   ▶ Akshit GUPTA Analysis of the Rogue Trader movie

   ▶ Akshit GUPTA History of Options markets

   ▶ Akshit GUPTA Option Trader – Job description

Useful Resources

Academic research

Hull J.C. (2015) Options, Futures, and Other Derivatives, Ninth Edition, Chapter 10 – Mechanics of options markets, 235-240.

Business analysis

CNBC Live option trading for APPLE stocks

About the author

Article written in June 2021 by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).