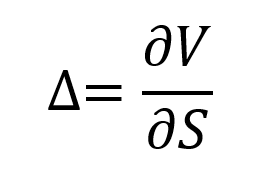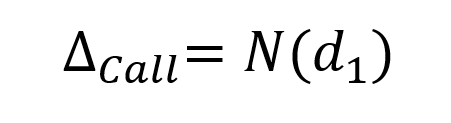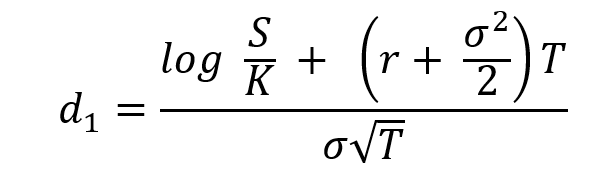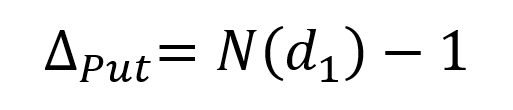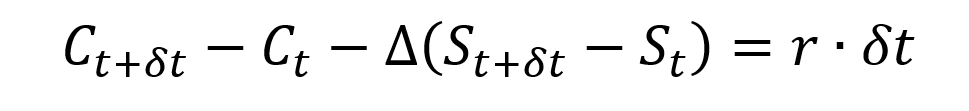Covered Call
This article written by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) presents the concept of covered call used in equities option contracts.
Introduction
Hedging is a strategy implemented by investors to reduce the risk in an existing investment. In financial markets, hedging is an effective tool used by investors to minimize the risk exposure and change the risk profile for any investment in securities. While hedging does not necessarily eliminate the entire risk for any investment, it does limit the potential losses that the investor can incur.
Option contracts are commonly used by market participants (traders, investors, asset managers, etc.) as hedging mechanisms due to their great flexibility (in terms of expiration date, moneyness, liquidity, etc.) and availability. Positions in options are used to offset the risk exposure in the underlying security, another option contract or in any other derivative contract. There are various popular strategies that can be implemented through option contracts to minimize risk and maximize returns, one of which is a covered call.
Covered call
The covered call strategy is a two-part strategy that essentially involves an investor writing a call option on an underlying security while simultaneously holding a long position in the same underlying. This action of buying an asset and writing calls on it at the same time is commonly referred as ‘buy write’. By writing a call option, the investor locks in the price of the underlying asset, thereby enjoying a short-term gain from the premium received.
Market scenario
The covered call is generally ideal if the investor has a neutral or slightly bullish outlook of the market wherein the potential future upside of the underlying asset owned by the investor is limited. This strategy is used by investors when they would prefer booking short-term profits on the assets than to keep holding it.
For instance, consider a ‘buy write’ situation where an investor buys shares of a stock (i.e., holds a long position in the stock) and simultaneously writes call options on them. The investor has a neutral view on the stock and doesn’t expect the price to rise much.
To book a short-term profit and also hedge any minor downsides in the stock price, the investor is writing call options on the stock at a strike price greater than or equal to the current price of the stock (i.e. out-of-the-money or at-the-money call options). The buyer of those call options would pay the investor a premium on those calls, whether or not the option is exercised. This is the covered call strategy in a nutshell.
Let us consider a covered call position with writing at-the money calls. One of following three scenarios may happen:
Scenario 1: the stock price does not change, and calls expire at the money
In this scenario, the market viewpoint of the investor holds correct and the profit from the strategy is the premium earned on the call options. In this case, the option holder does not exercise its call options, and the investor gets to keep the underlying stocks too.
Scenario 2: the stock price rises, and calls expire in the money
In this scenario, since the price of the stock was already locked in through the call, the investor enjoys a short-term profit along with the premium. However, this also poses a risk in case the price of the stock rises substantially because the investor misses out on the opportunity.
Scenario 3: the stock price falls and calls expire out of the money
This is a negative scenario for the investor. There is limited protection from the downside through the premium earned on the call options. However, if the stock price falls below a certain break-even point, the losses for the investor can be considerable since there will be a fall in its underlying position.
Risk profile
In a covered call, the total cost of the investment is equal to the price of the underlying asset minus the premium earned by writing the call. However, the profit potential for the investment is limited and the maximum loss can be significantly high. The risk profile of the position is represented in Figure 1.
Figure 1. Risk profile of covered call position.
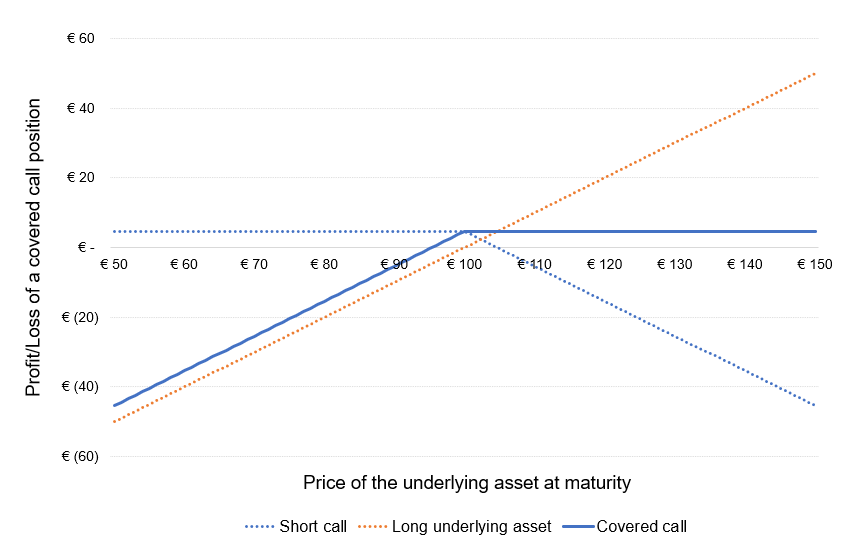
Source: computation by the author (based on the BSM model).
You can download below the Excel file for the computation of the Profit or Loss (P&L) function of the underlying position and covered call position.
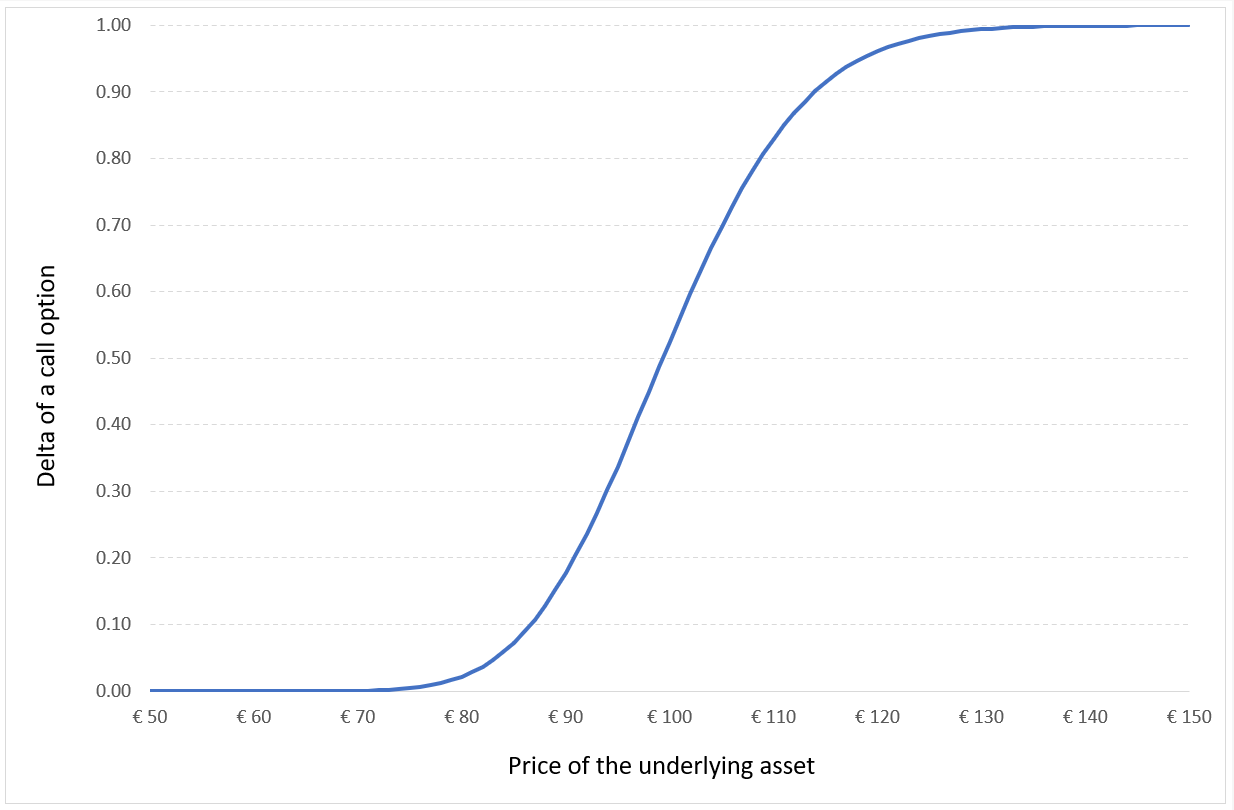
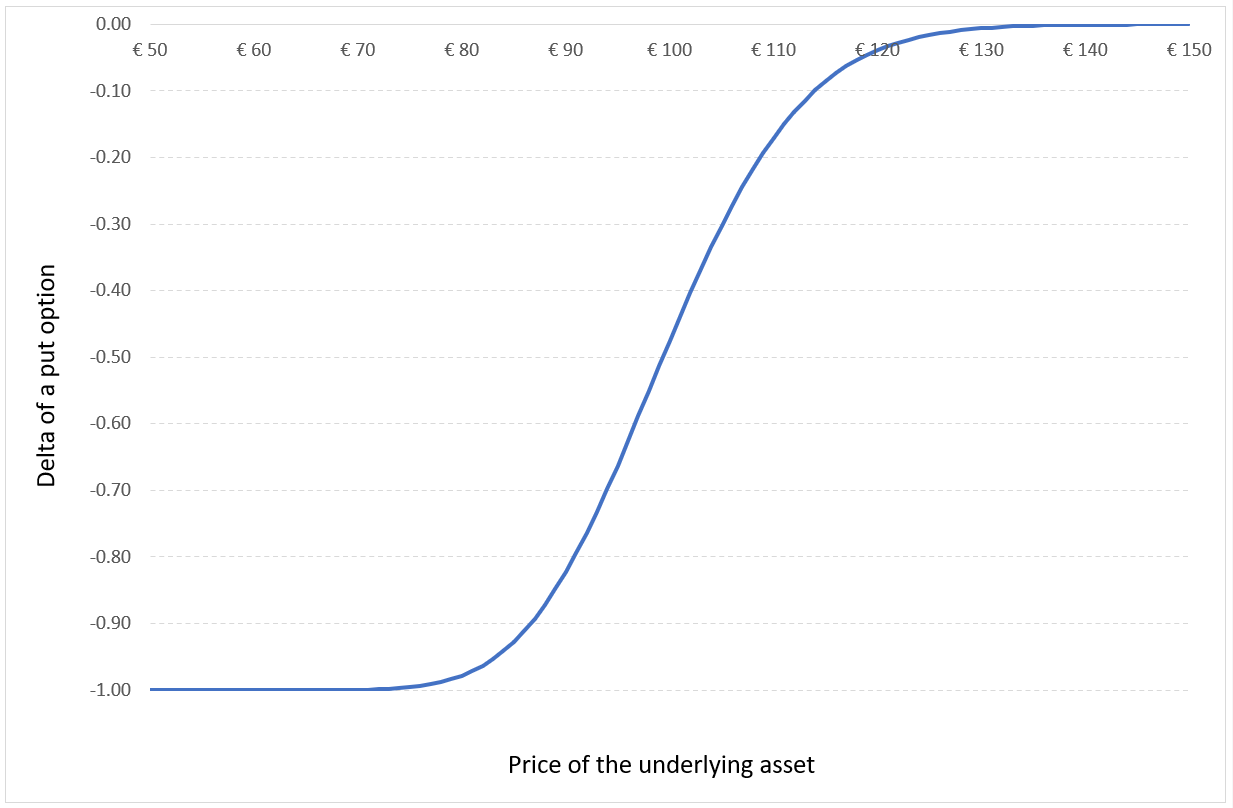
The delta of the position is equal to the sum of the delta of the long position in the underlying asset (+1) and the short position in the call option (-Δ).
Figure 2 represents the delta of the covered call position as a function of the price of the underlying asset. The delta of the call option is computed with the Black-Scholes-Merton model (BSM model).
Figure 2. Delta of a covered call position.
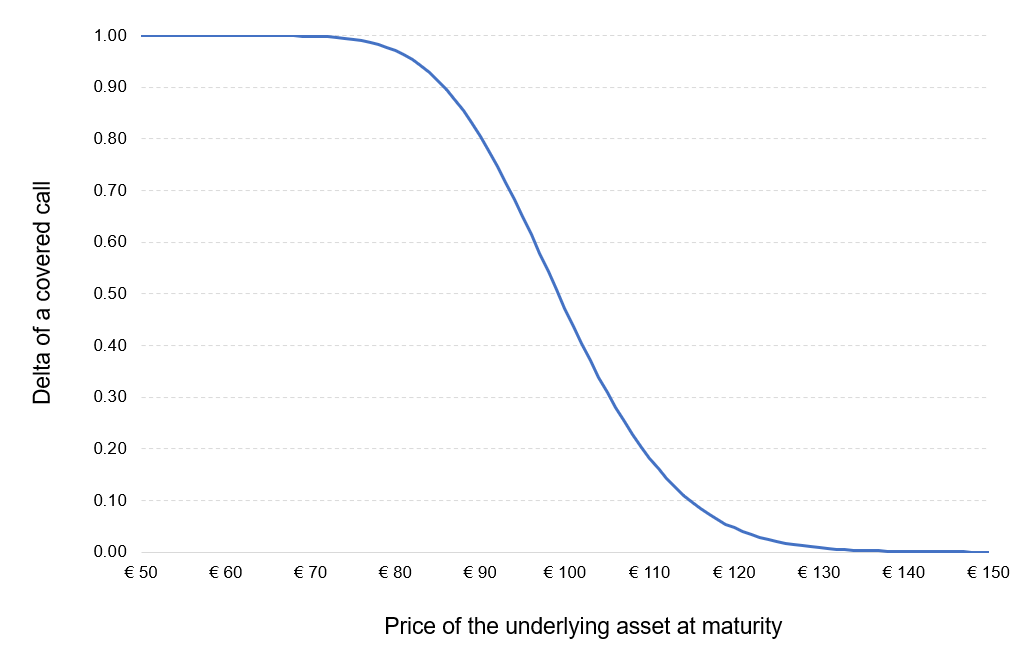
Source: computation by the author (based on the BSM model).
You can download below the Excel file for the computation of the delta of a protective put position.
Example
An investor holds 100 shares of Apple bought at the current price of $144 each. The total investment is then equal to $14,400. She is neutral about the short-term prospects of the market. In order to gain from her market scenario, she decides to write an at-the-money call option at $144 on the Apple stock (lot size is 100) with a maturity of one month, using the covered call strategy.
We use the following market data: the current price of Appel stock is $144, the implied volatility of Apple stock is 22.79%, and the risk-free interest rate is equal to 1.59%.
Based on the Black-Scholes-Merton model, the price of the call option is $3.87.
Let us consider three scenarios at the time of maturity of the call option:
Scenario 1: stability of the price of the underlying asset at $144
The total cost of the initial investment is the cost of acquiring the Apple stocks ($14,400) minus the premium received on writing the calls ($387 = $3.87*100), which is equal to $14,013, i.e. $14,400 – $387.
As the stock price ($144) is equal to the strike price of the call options ($144), the value of the call options is equal to zero, and the investor earns a profit which is equal to the initial price of the call options (the premium), which is equal to $387.
Scenario 2: an increase in the price of the underlying asset to $155
The total cost of the initial investment is the cost of acquiring the Apple stocks ($14,400) minus the premium on writing the calls ($387 = $3.87*100), which is equal to $14,013, i.e. $14,400 – $387.
As the stock price has risen to $155, the call options are exercised by the option buyer, and the investor will have to sell the Apple stocks at the strike price of $144.
By executing the covered call strategy, the investor earns $387 (i.e. ($144-$144)*100 +$387) but misses the opportunity of earning higher profits by selling the stock at the current market price of $155.
Scenario 3: a decrease in the price of the underlying asset to $142
The total cost of the initial investment is the cost of acquiring the Apple stocks ($14,400) minus the premium on writing the calls ($387 = $3.87*100), which is equal to $14,013, i.e. $14,400 – $387.
As the stock price is at $142, the call options are not exercised by the option buyer and the options expire worthless (out of the money).
As the buyer does not exercise the call options, the investor earns a profit which is equal to the price of the call options which is equal to $387. But his net profit decreases by the amount of the decrease in his position in the APPLE stocks which is equal to -$200 (i.e. ($142-$144)*100).
Related Posts
▶ Akshit GUPTA Options
▶ Akshit GUPTA Option Trader – Job description
▶ Akshit GUPTA The Black-Scholes-Merton model
▶ Akshit GUPTA Protective Put
▶ Akshit GUPTA Option Greeks – Delta
Useful Resources
Research articles
Black F. and M. Scholes (1973) “The Pricing of Options and Corporate Liabilities” The Journal of Political Economy, 81, 637-654.
Merton R.C. (1973) “Theory of Rational Option Pricing” Bell Journal of Economics, 4(1): 141–183.
Books
Hull J.C. (2015) Options, Futures, and Other Derivatives, Ninth Edition, Chapter 10 – Trading strategies involving Options, 276-295.
Wilmott P. (2007) Paul Wilmott Introduces Quantitative Finance, Second Edition, Chapter 8 – The Black Scholes Formula and The Greeks, 182-184.
About the author
Article written in December 2021 by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).