Dans cet article, Gabriel FILJA (ESSEC Business School, Executive Master in Senior Bank Management, 2022-2023 & Head of Hedging à Convera) présente des applications de la théorie des valeurs extrêmes en finance de marchés et notamment en gestion des risques de marchés.
Principe
La théorie des valeurs extrêmes (TVE), appelé théorème de Fisher-Tippet-Gnedenko tente de fournir une caractérisation complète du comportement de la queue pour tous les types de distributions de probabilités.
La théorie des valeurs extrêmes montre que la loi asymptotique des rentabilités minimale et maximale a une forme bien déterminée qui est largement indépendante du processus de rentabilités lui-même (le lien entre les deux distributions apparaît en particulier dans la valeur de l’indice de queue qui reflète le poids des queues de distribution). L’intérêt de la TVE dans la gestion du risque c’est de pouvoir calculer le quantile au-delà de 99% du seuil de confiance dans le cadre des stress tests ou de la publication des exigences réglementaires.
Gnedenko a démontré en 1943 par la Théorie des valeurs extrêmes la propriété qui s’applique à des nombreuses distributions de probabilités. Soit F(x) la fonction de répartition d’une variable x. u est une valeur de x située dans la partie droite de la queue de distribution.
La probabilité que x soit compris entre u et u+y est de F(y+u) – F(u) et la probabilité que x soit supérieur à u est 1-F(u). Soit Fu(y) la probabilité conditionnelle que x soit compris entre u et u+y sachant que x>u∶
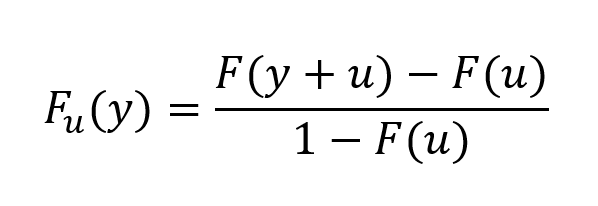
Estimation des paramètres
Selon les résultats de Gnedenko, pour un grand nombre de distribution, cela converge vers une distribution généralisée de Pareto au fur et à mesure que u augmente :
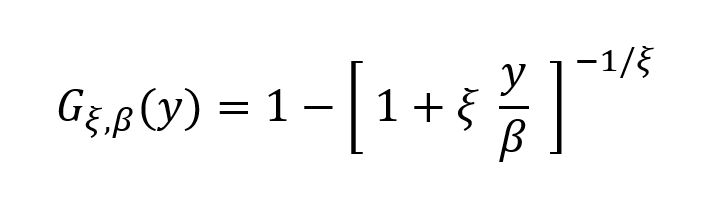
β est le paramètre d’échelle représente la dispersion de la loi des extrêmes
ξ est l’indice de queue qui mesure l’épaisseur de la queue et la forme
Selon la valeur de l’indice de queue, on distingue trois formes dedistribiution d’extrêmes :
- Frechet ξ > 0
- Weibull ξ < 0
- Gumbel ξ = 0
L’indice de queue ξ reflète le poids des extrêmes dans la distribution des rentabilités. Une valeur positive de l’indice de queue signifie que les extrêmes n’ont pas de rôle important puisque la variable est bornée. Une valeur nulle donne relativement peu d’extrêmes alors qu’une valeur négative implique un grand nombre d’extrêmes (c’est le cas de la loi normale).
Figure 1 : Densité des lois des valeurs extrêmes
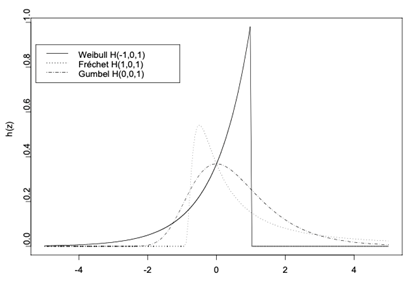
Source : auteur.
Tableau 1 : Fonctions de distribution des valeurs extrêmes pour un ξ > 0, loi de Frechet, ξ < 0 loi de Weibull et ξ = 0, loi de Gumbel. 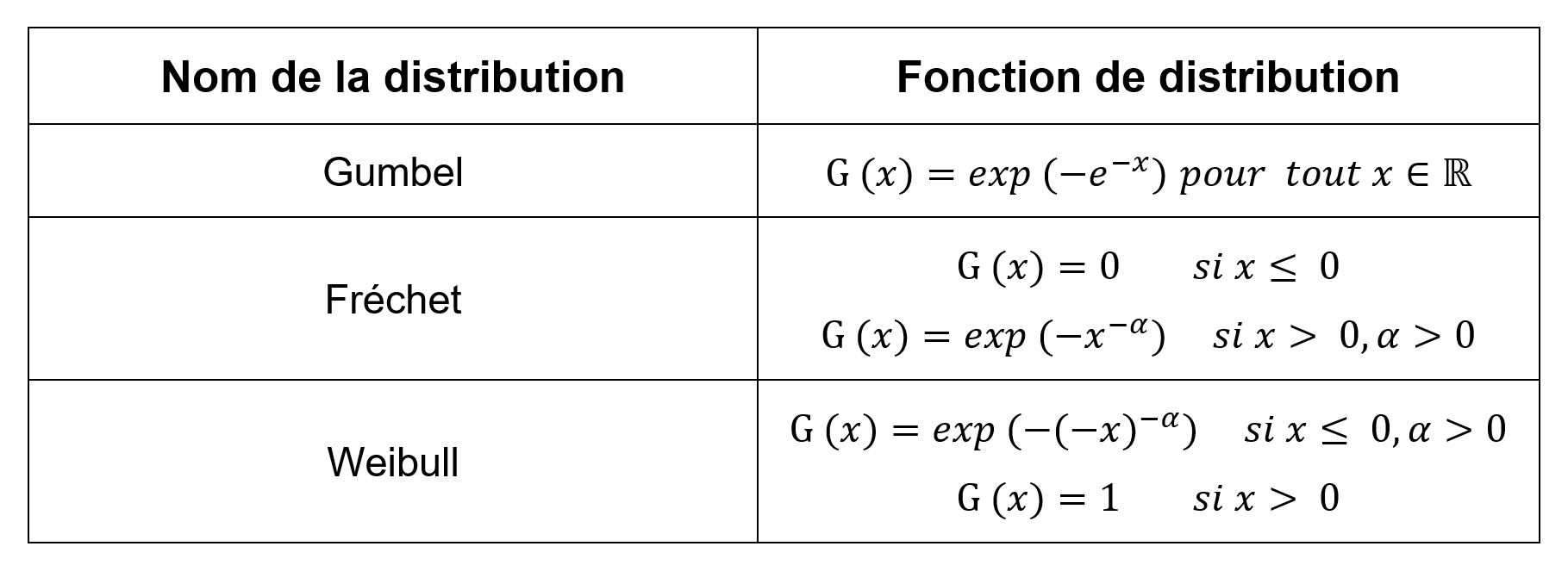
Source : auteur.
Les paramètres β et ξ sont estimés par la méthode de maximum de vraisemblance. D’abord il faut définir u (valeur proche du 95e centile par exemple). Une des méthodes pour déterminer ce seuil, c’est la technique appelée Peak Over Threshold (POT), ou méthode des excès au-delà d’un seuil qui se focalise sur les observations qui dépassent un certain seuil donné. Au lieu de considérer les valeurs maximales ou les plus grandes valeurs, cette méthode consiste à examiner toutes les observations qui franchissent un seuil élevé préalablement fixé.
L’objectif est de sélectionner un seuil adéquat et d’analyser les excès qui en découlent. Ensuite nous trions les résultats par ordre décroissant pour obtenir les observations telles que x>u et leur nombre total.
Nous étudions maintenant les rentabilités extrêmes pour l’action Société Générale sur la période 2011-2021. La Figure 2 représentes rentabilités journalières de l’action et les rentabilités extrêmes négatives obtenues avec l’approche des dépassements de seuil (Peak Over Threshold ou POT). Avec le seuil retenu de -7%, on obtient 33 dépassements sur 2 595 rentabilités journalières de la période 2011 à 2021.
Figure 2 : Sélection des rentabilités extrêmes négatives pour l’action Société Générale selon l’approche Peak Over Threshold (POT)
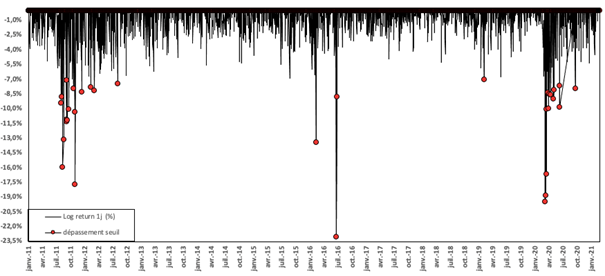
Source : auteur.
Méthode d’estimation statistique
Nous allons maintenant voir comment déterminer les β et ξ en utilisant la fonction de maximum de vraisemblance qui s’écrit :
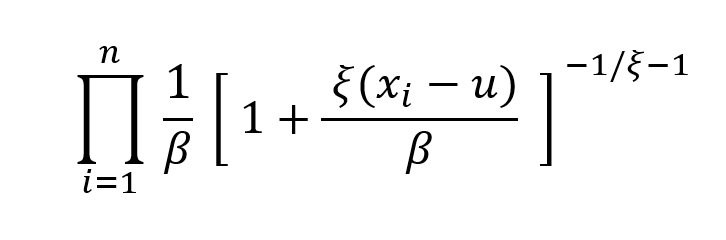
Pour un échantillon de n observations, l’estimation de 1-F(u) est nu/n. Dans ce cas, la probabilité inconditionnelle de x>u+y vaut :
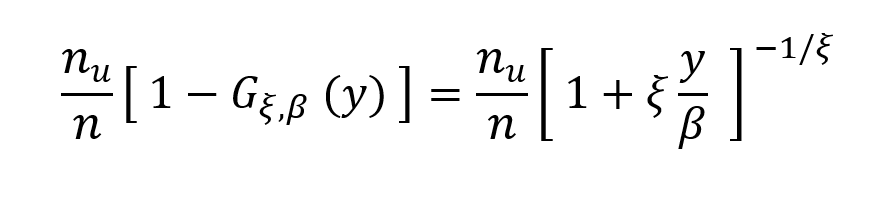
Et l’estimateur de la queue de distribution de probabilité cumulée de x (pour un grand) est :
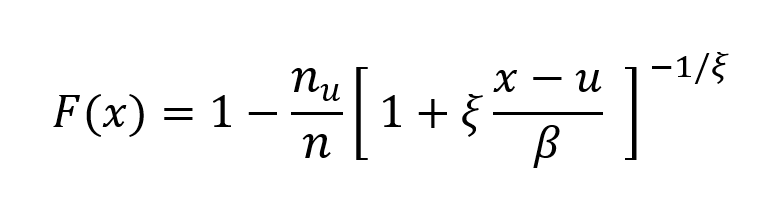
Mon travail personnel a consisté à estimer le paramètre d’échelle β et le paramètre de queue ξ à partir de la formule par le maximum de vraisemblance en utilisant le solveur Excel. Nous avons précédemment déterminé n=0,07 par la méthode de POT en Figure 2, et n_u= 2595
Ainsi nous obtenons β=0,0378 et ξ=0,0393 ce qui maximise par la méthode du maximum de vraisemblance la somme du logarithme des valeurs extrêmes à un total de 73,77.
Estimation de la VaR TVE
Pour calculer le VaR au seuil q, nous obtenons F(VaR) = q
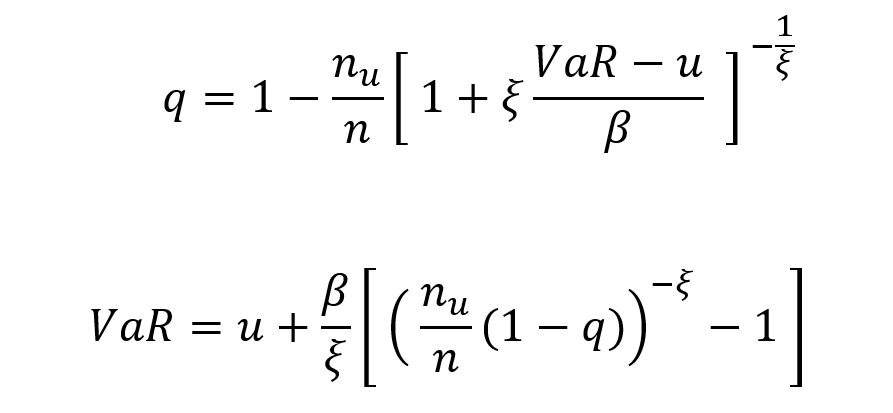
Mon travail personnel a consisté à estimer la VaR du titre de la Société Générale de la période de 2011 à 2021 sur un total de 2595 cotations avec 33 dépassements de seuil (-7%). En appliquant les données obtenues à la formule nous obtenons :
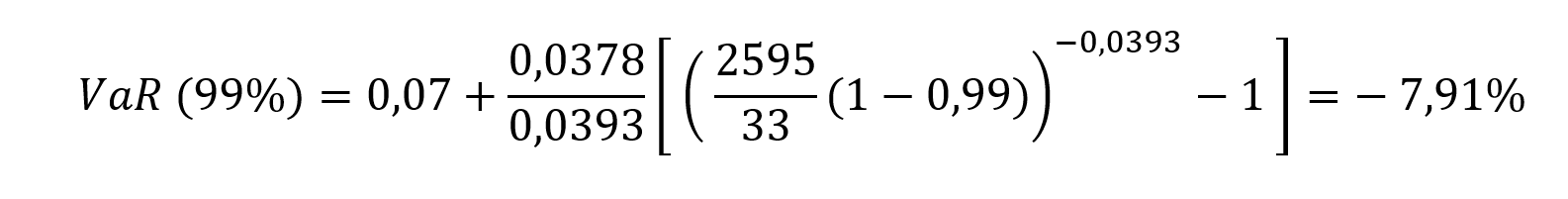
Puis nous estimons la VaR à 99,90% et 99,95% :
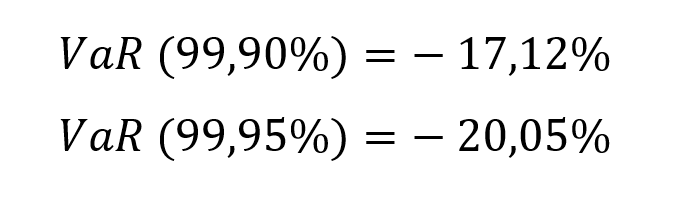
Il n’est pas surprenant que l’extrapolation à la queue d’une distribution de probabilité soit difficile, pas parce qu’il est difficile d’identifier des distributions de probabilité possibles qui pourraient correspondre aux données observées (il est relativement facile de trouver de nombreuses distributions possibles différentes), mais parce que l’éventail des réponses qui peuvent vraisemblablement être obtenues peut être très large, en particulier si nous voulons extrapoler dans la queue lointaine où il peut y avoir peu ou pas de points d’observation directement applicables.
La théorie des valeurs extrêmes, si elle est utilisée pour modéliser le comportement de la queue au-delà de la portée de l’ensemble de données observées, est une forme d’extrapolation. Une partie de la cause du comportement à queue épaisse (fat tail) est l’impact que le comportement humain (y compris le sentiment des investisseurs) a sur le comportement du marché.
En quoi ça peut m’intéresser ?
Nous pouvons ainsi mener des stress tests en utilisant la théorie des valeurs extrêmes et évaluer les impacts sur le bilan de la banque ou encore déterminer les limites de risques pour le trading et obtenir ainsi une meilleure estimation du worst case scenario.
Autres articles sur le blog SimTrade
▶ Shengyu ZHENG Catégories de mesures de risques
▶ Shengyu ZHENG Moments de la distribution
▶ Shengyu ZHENG Extreme Value Theory: the Block-Maxima approach and the Peak-Over-Threshold approach
Ressources
Articles académiques
Falk M., J. Hüsler, et R.-D. Reiss, Laws of Small Numbers: Extremes and Rare Events. Basel: Springer Basel, 2011. doi: 10.1007/978-3-0348-0009-9.
Gilli M. et E. Këllezi, « An Application of Extreme Value Theory for Measuring Financial Risk », Comput Econ, vol. 27, no 2, p. 207‑228, mai 2006, doi: 10.1007/s10614-006-9025-7.
Gkillas K. and F. Longin (2018) Financial market activity under capital controls: lessons from extreme events Economics Letters, 171, 10-13.
Gnedenko B., « Sur La Distribution Limite Du Terme Maximum D’Une Serie Aleatoire », Annals of Mathematics, vol. 44, no 3, p. 423‑453, 1943, doi: 10.2307/1968974.
Hull J.et A. White, « Optimal delta hedging for options », Journal of Banking & Finance, vol. 82, p. 180‑190, sept. 2017, doi: 10.1016/j.jbankfin.2017.05.006.
Longin F. (1996) The asymptotic distribution of extreme stock market returns Journal of Business, 63, 383-408.
Longin F. (2000) From VaR to stress testing : the extreme value approach Journal of Banking and Finance, 24, 1097-1130.
Longin F. (2016) Extreme events in finance: a handbook of extreme value theory and its applications Wiley Editions.
Longin F. and B. Solnik (2001) Extreme Correlation of International Equity Markets, The Journal of Finance, 56, 649-676.
Roncalli T. et G. Riboulet, « Stress testing et théorie des valeurs extrêmes : une vision quantitée du risque extrême ».
Sites internet
A propos de l’auteur
Cet article a été écrit en juillet 2023 par Gabriel FILJA (ESSEC Business School, Executive Master in Senior Bank Management, 2022-2023 & Head of Hedging à Convera).