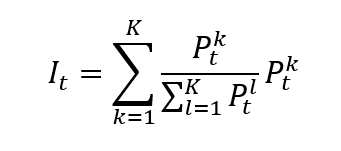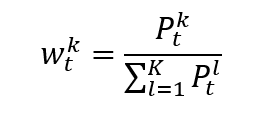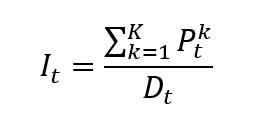Extreme returns and tail modelling of the Nikkei 225 index for the Japanese equity market

November 23, 2023 by Shengyu ZHENG

Extreme returns and tail modelling of the Nikkei 225 index for the Japanese equity market

In this article, Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2024) describes the statistical behavior of extreme returns of the Nikkei 225 index for the Japanese equity market and explains how extreme value theory can be used to model the tails of its distribution.

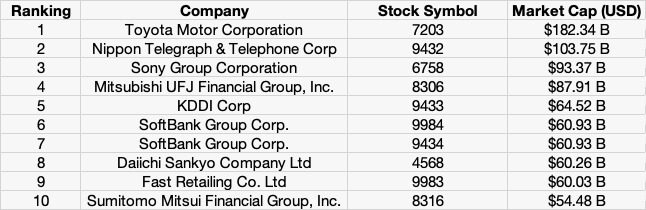
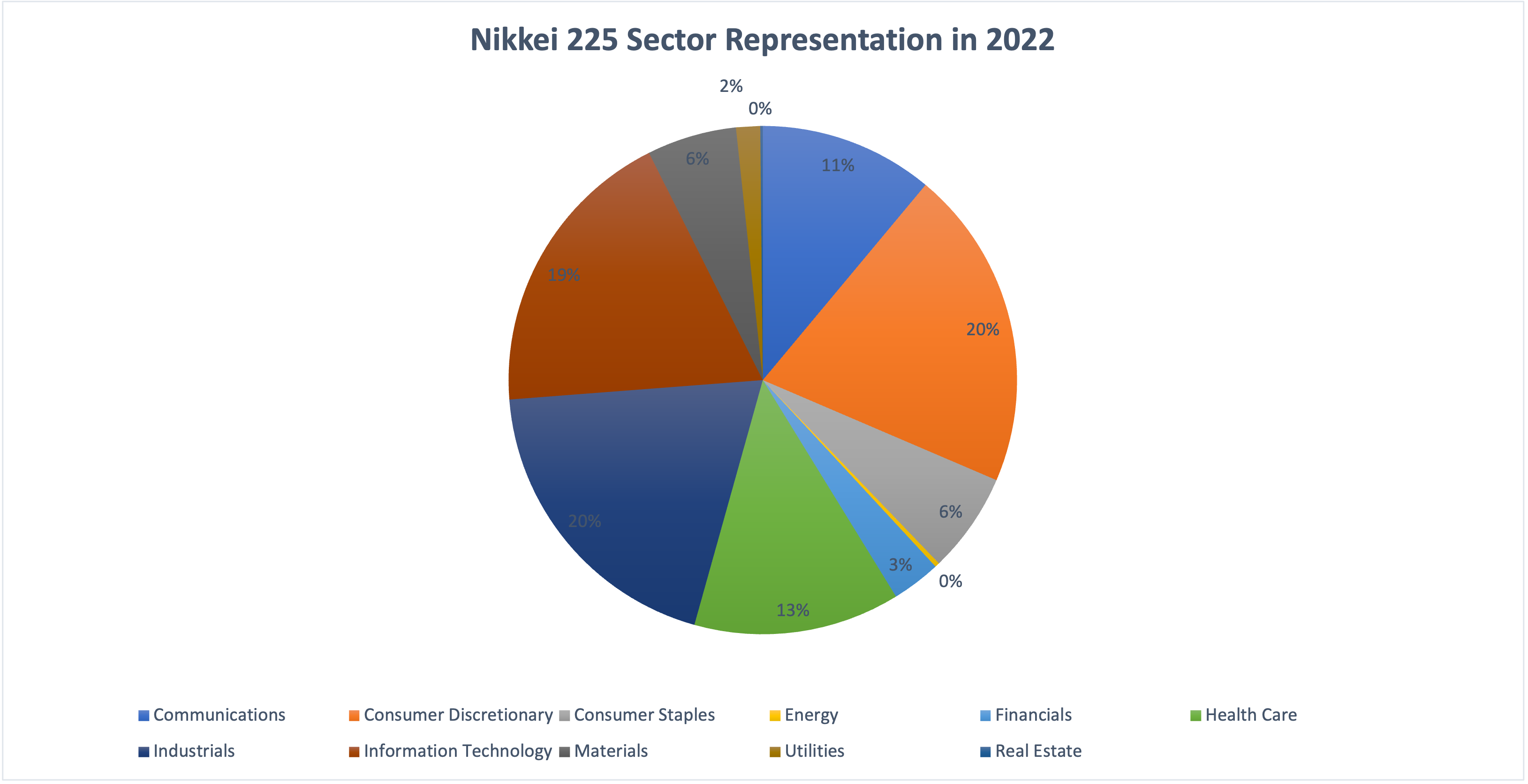
The Nikkei 225 index for the Japanese equity market

The Nikkei 225, often simply referred to as the Nikkei, is a stock market index representing the performance of 225 major companies listed on the Tokyo Stock Exchange (TSE). Originating in 1950, this index has become a symbol of Japan’s economic prowess and serves as a crucial benchmark in the Asian financial markets. Comprising companies across diverse sectors such as technology, automotive, finance, and manufacturing, the Nikkei 225 offers a comprehensive snapshot of the Japanese economic landscape, reflecting the nation’s technological innovation, industrial strength, and global economic influence.

Utilizing a price-weighted methodology, the Nikkei 225 calculates its value based on stock prices rather than market capitalization, distinguishing it from many other indices. This approach means that higher-priced stocks have a more significant impact on the index’s movements. Investors and financial analysts worldwide closely monitor the Nikkei 225 for insights into Japan’s economic trends, market sentiment, and investment opportunities. As a vital indicator of the direction of the Japanese stock market, the Nikkei 225 continues to be a key reference point for making informed investment decisions and navigating the complexities of the global financial landscape.

In this article, we focus on the Nikkei 225 index of the timeframe from April 1st, 2015, to April 1st, 2023. Here we have a line chart depicting the evolution of the index level of this period.

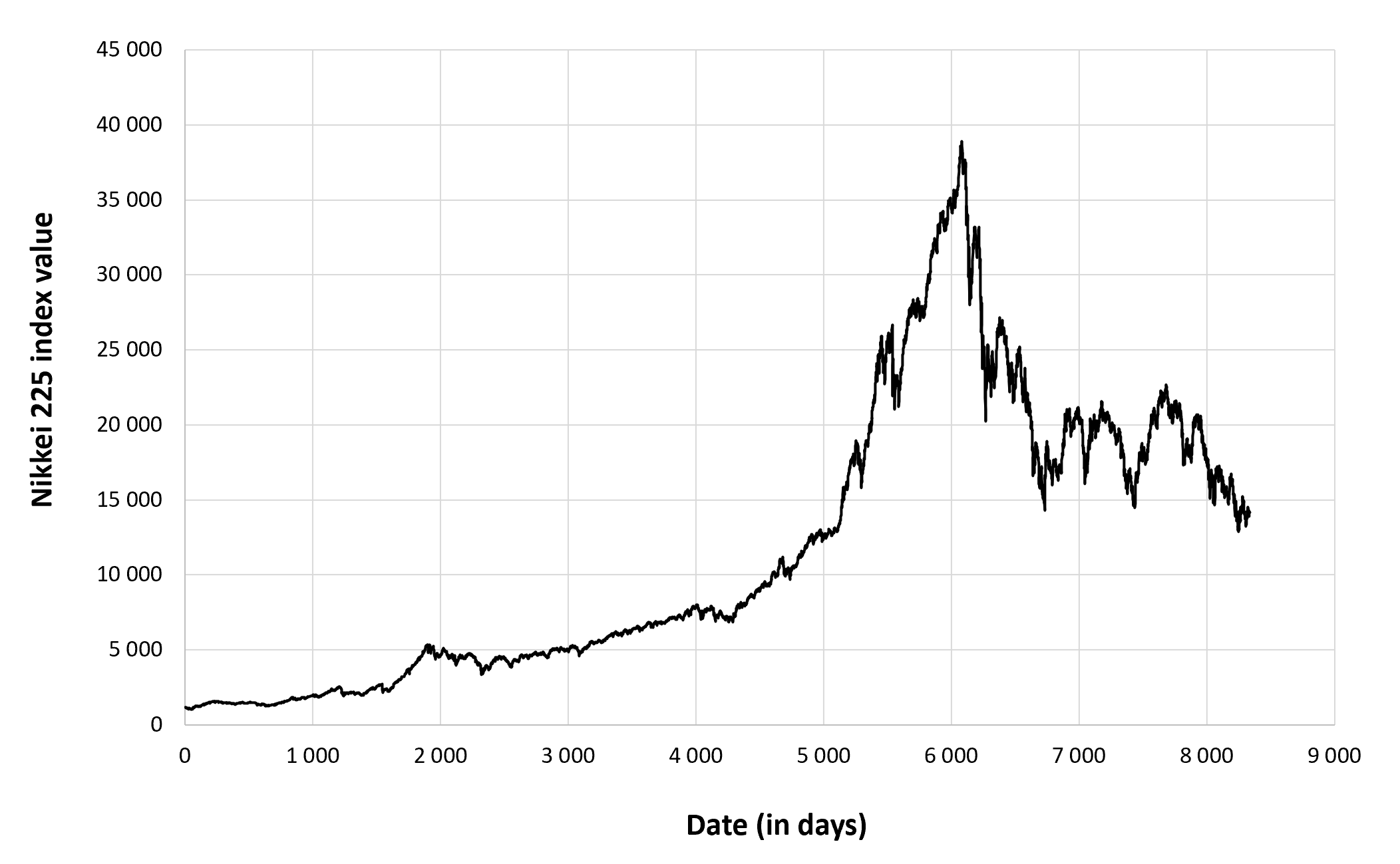
Figure 1 below gives the evolution of the Nikkei 225 index from April 1, 2015 to April 1, 2023 on a daily basis.

Figure 1. Evolution of the Nikkei 225 index.

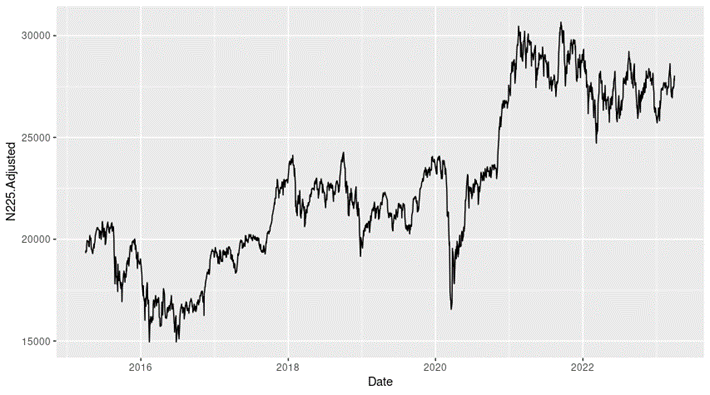
Source: computation by the author (data: Yahoo! Finance website).

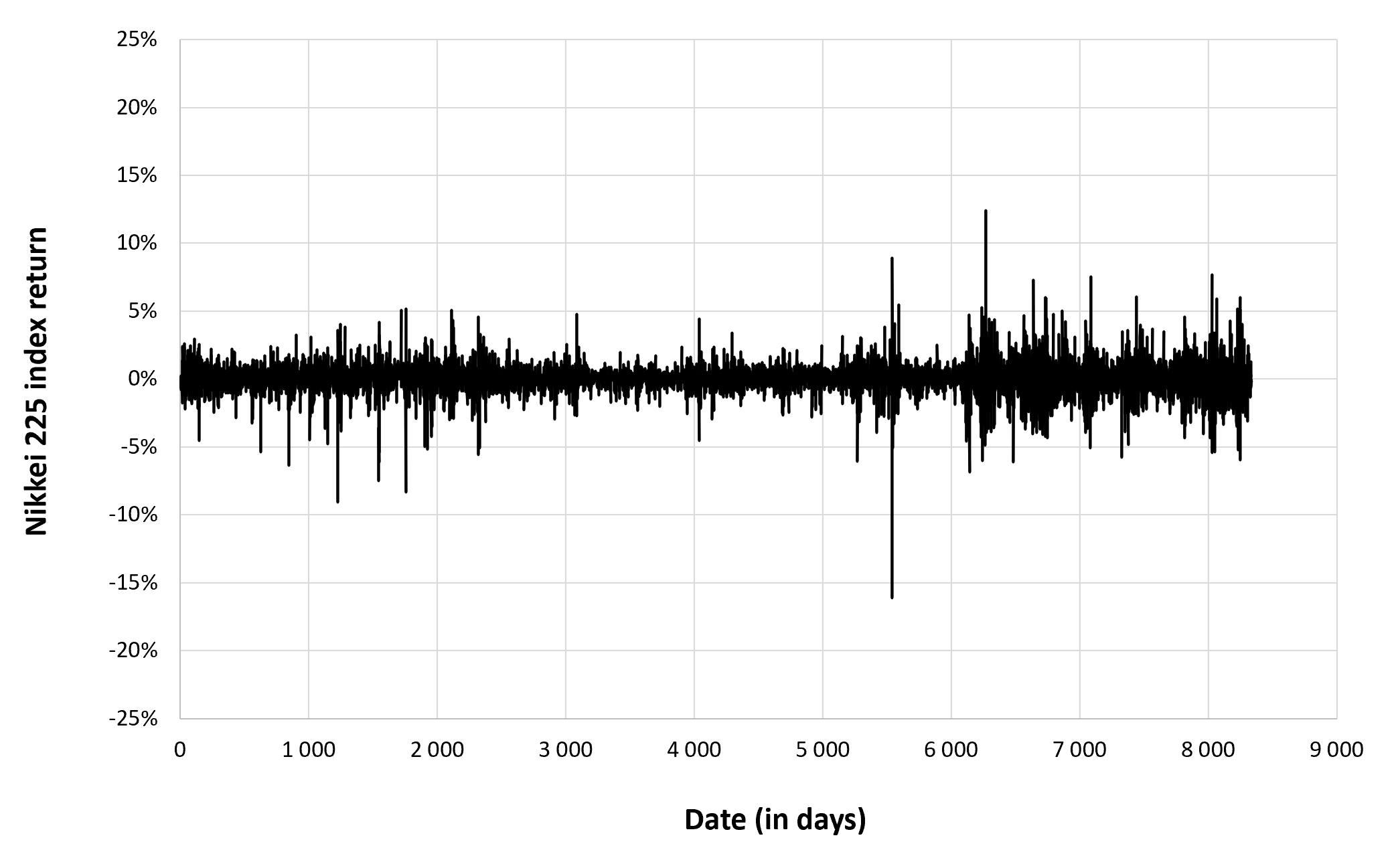
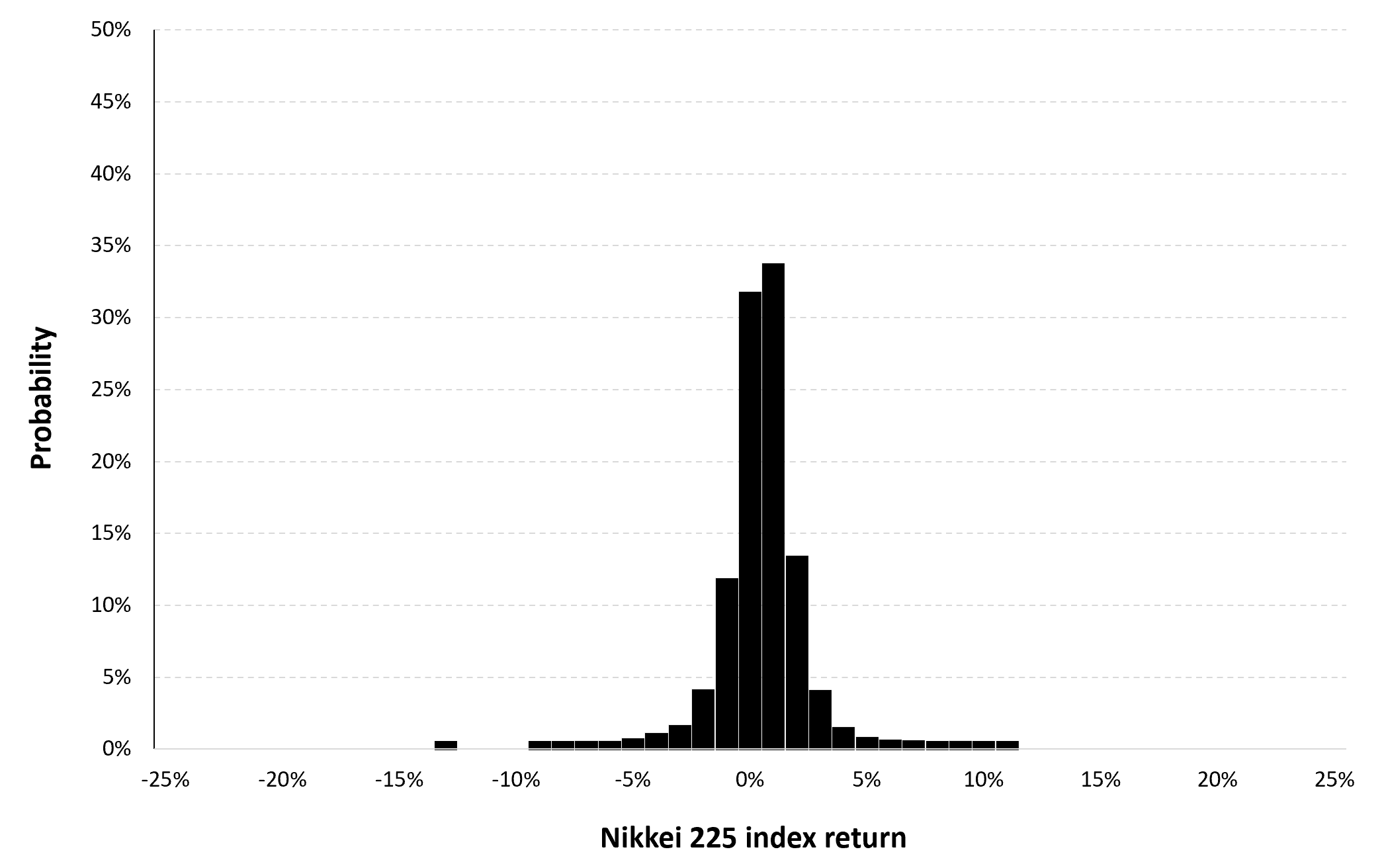
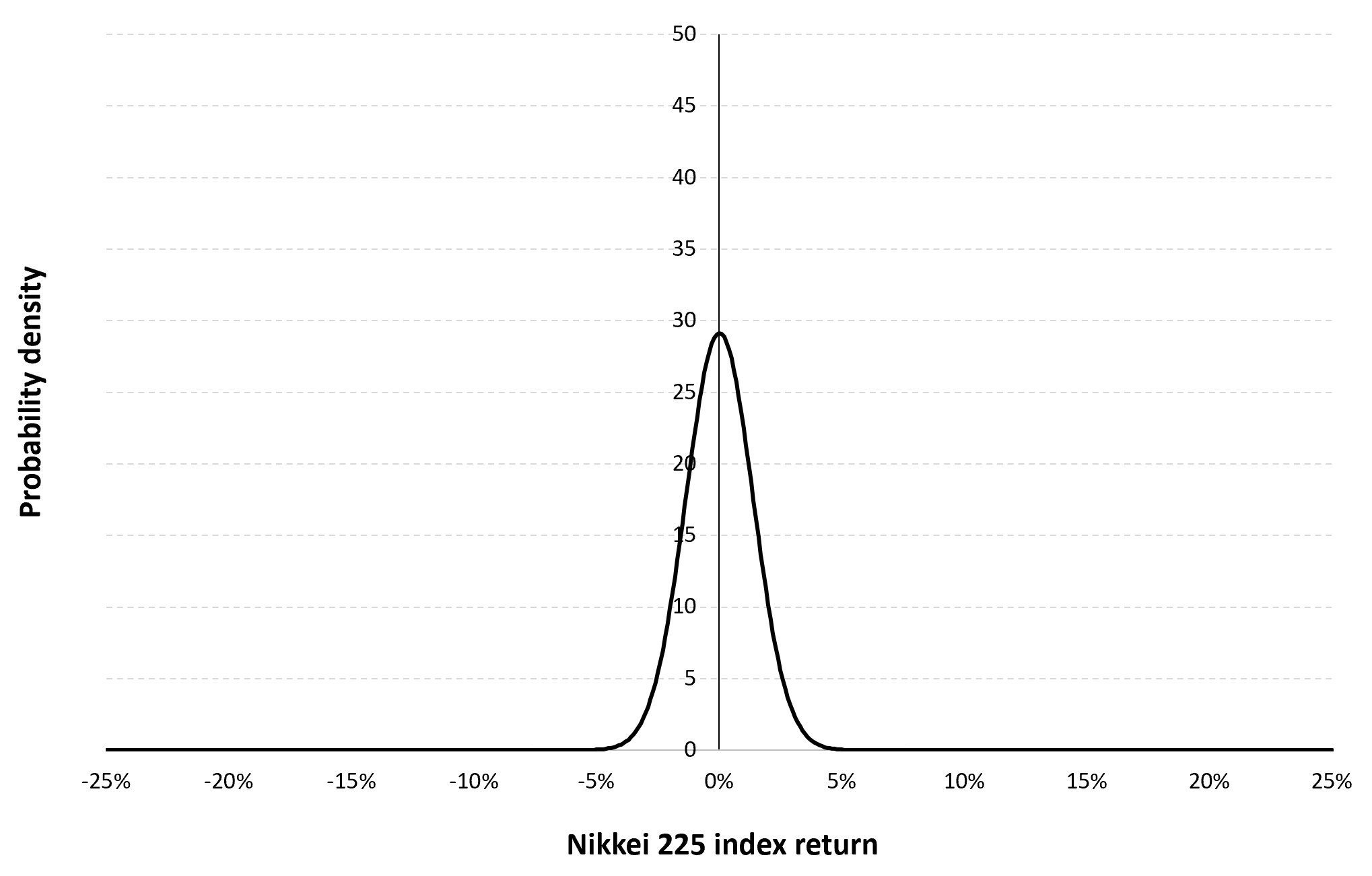
Figure 2 below gives the evolution of the daily logarithmic returns of Nikkei 225 index from April 1, 2015 to April 1, 2023 on a daily basis. We observe concentration of volatility reflecting large price fluctuations in both directions (up and down movements). This alternation of periods of low and high volatility is well modeled by ARCH models.

Figure 2. Evolution of the Nikkei 225 index logarithmic returns.

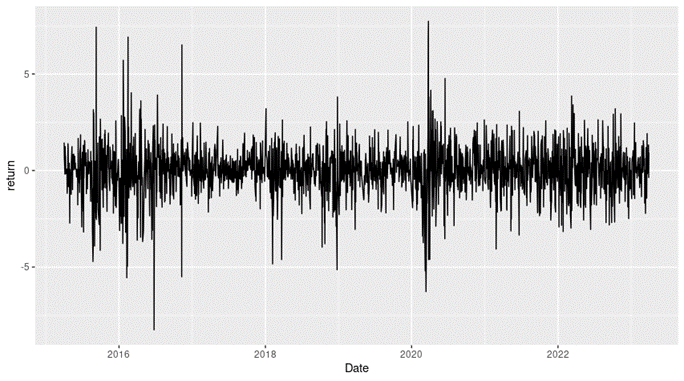
Source: computation by the author (data: Yahoo! Finance website).

Summary statistics for the Nikkei index

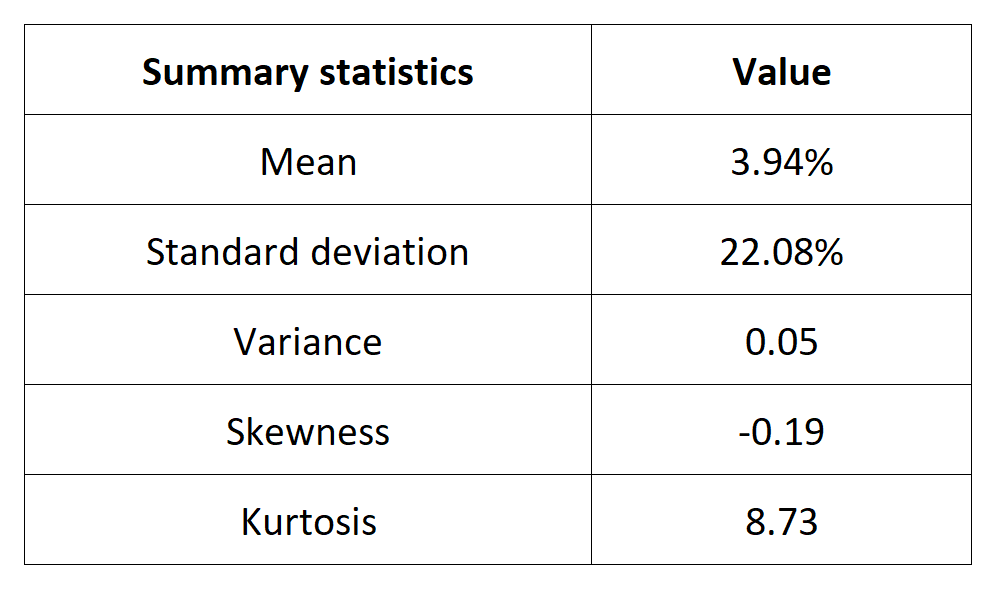
Table 1 below presents the summary statistics estimated for the Nikkei 225 index:

Table 1. Summary statistics for the Nikkei 225 index.
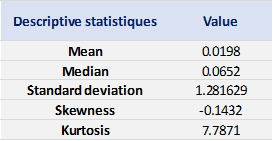
summary statistics of the Nikkei 225 index returns
Source: computation by the author (data: Yahoo! Finance website).

The mean, the standard deviation / variance, the skewness, and the kurtosis refer to the first, second, third and fourth moments of statistical distribution of returns respectively. We can conclude that during this timeframe, the Nikkei 225 index takes on a slight upward trend, with relatively important daily deviation, negative skewness and excess of kurtosis.

Tables 2 and 3 below present the top 10 negative daily returns and top 10 positive daily returns for the index over the period from April 1, 2015 to April 1, 2023.

Table 2. Top 10 negative daily returns for the Nikkei 225 index.
Top 10 negative returns of the Nikkei 225 index
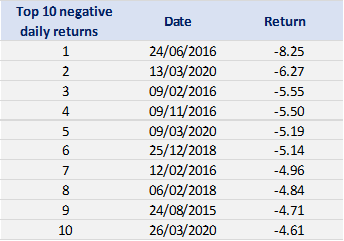
Source: computation by the author (data: Yahoo! Finance website).

Table 3. Top 10 positive daily returns for the Nikkei 225 index.
Top 10 positive returns of the Nikkei 225 index
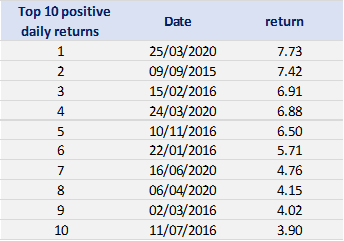
Source: computation by the author (data: Yahoo! Finance website).

Modelling of the tails

Here the tail modelling is conducted based on the Peak-over-Threshold (POT) approach which corresponds to a Generalized Pareto Distribution (GPD). Let’s recall the theoretical background of this approach.

The POT approach takes into account all data entries above a designated high threshold u. The threshold exceedances could be fitted into a generalized Pareto distribution:

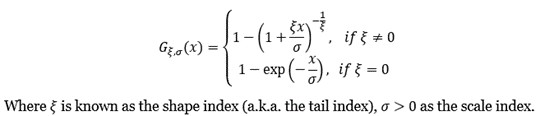
Illustration of the POT approach

An important issue for the POT-GPD approach is the threshold selection. An optimal threshold level can be derived by calibrating the tradeoff between bias and inefficiency. There exist several approaches to address this problematic, including a Monte Carlo simulation method inspired by the work of Jansen and de Vries (1991). In this article, to fit the GPD, we use the 2.5% quantile for the modelling of the negative tail and the 97.5% quantile for that of the positive tail.

Based on the POT-GPD approach with a fixed threshold selection, we arrive at the following modelling results for the GPD for negative extreme returns (Table 4) and positive extreme returns (Table 5) for the Nikkei 225 index:

Table 4. Estimate of the parameters of the GPD for negative daily returns for the Nikkei 225 index.
Modelling of negative extreme returns of the Nikkei 225 index
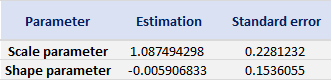
Source: computation by the author (data: Yahoo! Finance website).

Table 5. Estimate of the parameters of the GPD for positive daily returns for the Nikkei 225 index.
Modelling of positive extreme returns of the Nikkei 225 index
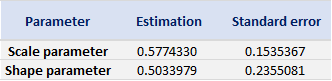
Source: computation by the author (data: Yahoo! Finance website).

Figure 3. GPD for the left tail of the Nikkei 225 index returns.

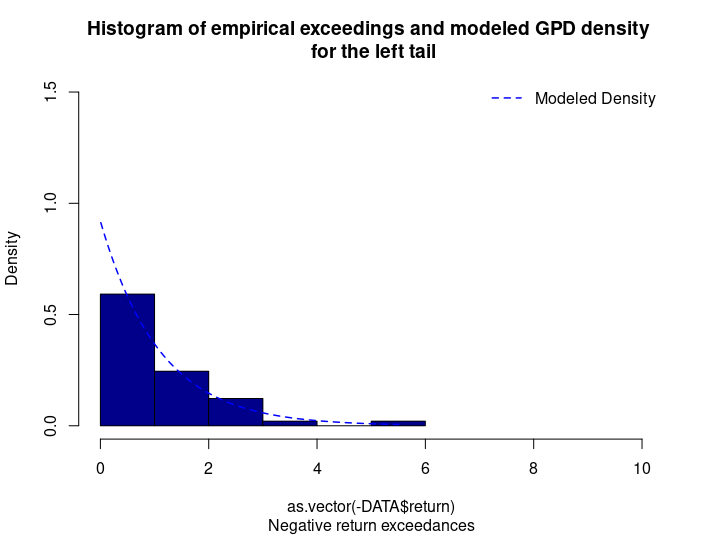
Source: computation by the author (data: Yahoo! Finance website).

Figure 4. GPD for the right tail of the Nikkei 225 index returns.

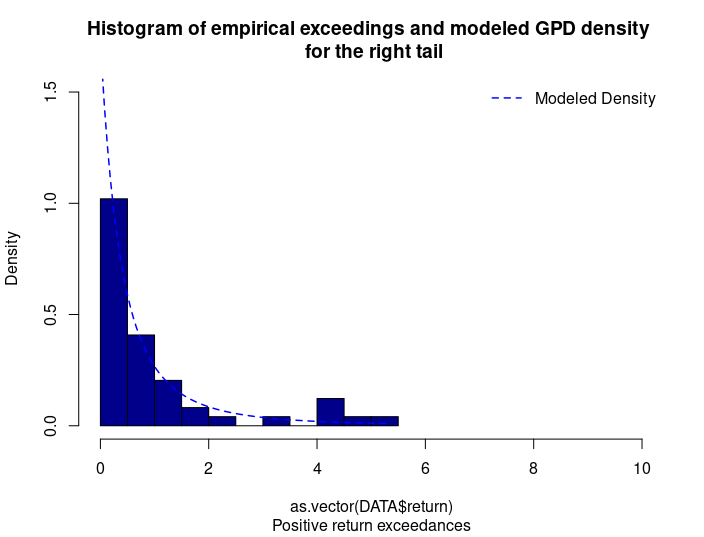
Source: computation by the author (data: Yahoo! Finance website).

Applications in risk management

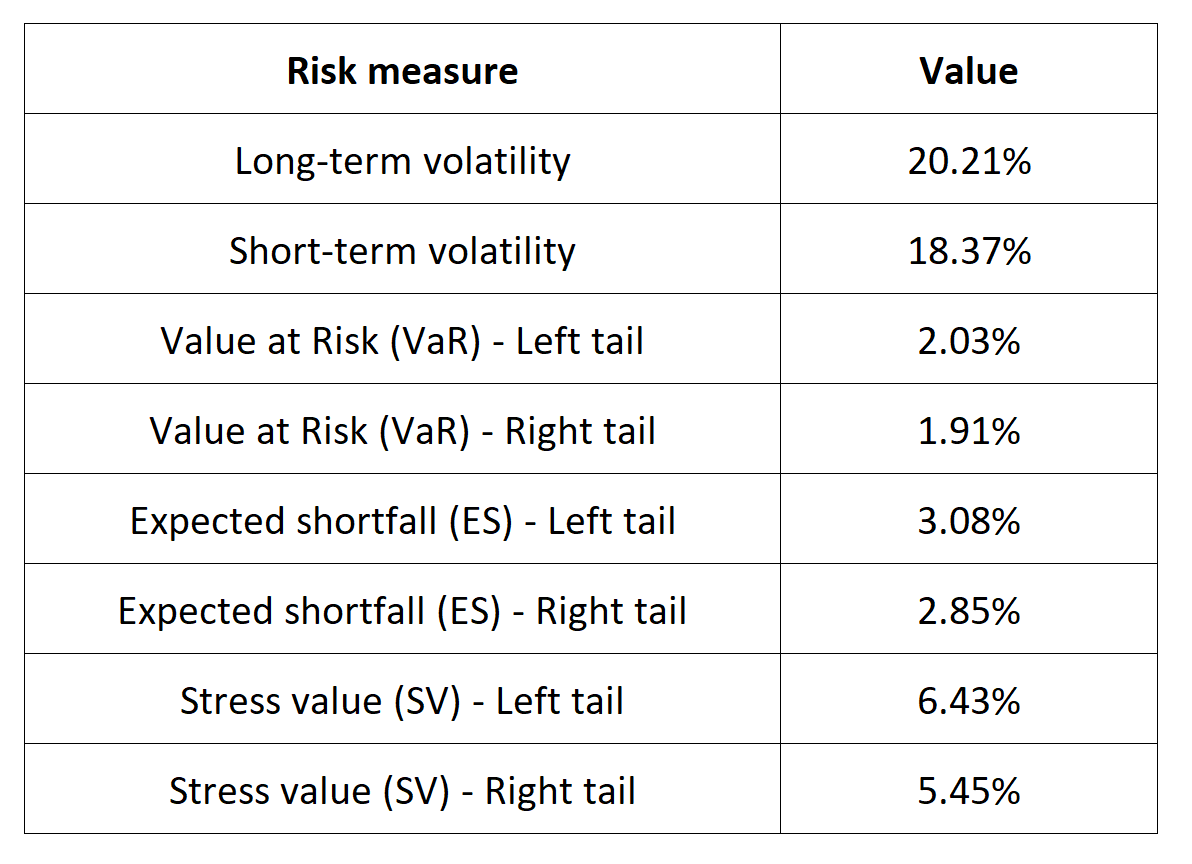
Extreme Value Theory (EVT) as a statistical approach is used to analyze the tails of a distribution, focusing on extreme events or rare occurrences. EVT can be applied to various risk management techniques, including Value at Risk (VaR), Expected Shortfall (ES), and stress testing, to provide a more comprehensive understanding of extreme risks in financial markets.

Why should I be interested in this post?

Extreme Value Theory is a useful tool to model the tails of the evolution of a financial instrument. In the ever-evolving landscape of financial markets, being able to grasp the concept of EVT presents a unique edge to students who aspire to become an investment or risk manager. It not only provides a deeper insight into the dynamics of equity markets but also equips them with a practical skill set essential for risk analysis. By exploring how EVT refines risk measures like Value at Risk (VaR) and Expected Shortfall (ES) and its role in stress testing, students gain a valuable perspective on how financial institutions navigate during extreme events. In a world where financial crises and market volatility are recurrent, this post opens the door to a powerful analytical framework that contributes to informed decisions and financial stability.

Download R file to model extreme behavior of the index

You can find below an R file (file with txt format) to study extreme returns and model the distribution tails for the Nikkei 225 index.

Useful resources

Academic resources

Embrechts P., C. Klüppelberg and T. Mikosch (1997) Modelling Extremal Events for Insurance and Finance Springer-Verlag.

Embrechts P., R. Frey, McNeil A.J. (2022) Quantitative Risk Management Princeton University Press.

Gumbel, E. J. (1958) Statistics of extremes New York: Columbia University Press.

Longin F. (2016) Extreme events in finance: a handbook of extreme value theory and its applications Wiley Editions.

Other resources

Extreme Events in Finance

Chan S. Statistical tools for extreme value analysis

Rieder H. E. (2014) Extreme Value Theory: A primer (slides).

About the author

The article was written in November 2023 by Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2024).

The Nikkei 225 index

April 22, 2023 by Nithisha CHALLA

The Nikkei 225 index

In this article, Nithisha CHALLA (ESSEC Business School, Grande Ecole Program – Master in Management, 2021-2023) presents the Nikkei 225 index and details its characteristics.

The Nikkei 225 index

The Nikkei 225 index is considered as the primary benchmark index of the Tokyo Stock Exchange (TSE) and is the most widely quoted average of Japanese equities. One of Japan’s top newspapers, the Nihon Keizai Shimbun (Nikkei), first published the index in 1950. The index consists of 225 blue-chip companies listed on the TSE, which are considered to represent the overall health of the Japanese economy. These companies come from various industries such as finance, technology, automobile, and retail, among others.

The Financial Times, a preeminent global provider of financial news, was purchased by Nikkei Inc, the parent company of Nikkei, for $1.3 billion in 2015. This acquisition highlighted Nikkei’s growing global presence and ambition to diversify beyond the Japanese market. The Nikkei 225 index follows a price-weighted methodology. This means that the components of the index are weighted based on their stock price, with higher-priced stocks carrying a greater weight in the index.

In the past few years, the Nikkei 225 index has been affected by various economic and political events, such as the COVID-19 pandemic and the Tokyo Olympics. The pandemic caused the index to significantly decline in 2020, but it has since recovered and reached new highs in 2021.

How is the Nikkei 225 index represented in trading platforms and financial websites? The ticker symbol used in the financial industry for the Nikkei 225 index is “NI225”.

Table 1 below gives the Top 10 stocks in the Nikkei 225 index in terms of market capitalization as of January 31, 2023.

Table 1. Top 10 stocks in the Nikkei index.
Top 10 stocks in the Nikkei 225 index
Source: computation by the author (data: YahooFinance! financial website).

Table 2 below gives the sector representation of the Nikkei 225 index in terms of number of stocks and market capitalization as of January 31, 2023.

Table 2. Sector representation in the Nikkei 225 index.

Source: computation by the author (data: YahooFinance! financial website).

Calculation of the Nikkei 225 index value

The Nikkei 225 index is calculated using a price-weighted methodology. This means that the price of each stock in the index is multiplied by the number of shares outstanding to determine the total market value of the company. The Nikkei 225 index is frequently used as a leading indicator of the state of the Japanese stock market, and economy, and as a gauge of trends in the world economy.

The formula to compute the Nikkei 225 is given by

A price-weighted index is calculated by summing the prices of all the assets in the index and dividing by a divisor equal to the number of assets.

The formula for a price-weighted index is given by

Price-weighted index value

where I is the index value, k a given asset, K the number of assets in the index, P^k the market price of asset k, and t the time of calculation of the index.

In a price-weighted index, the weight of asset k is given by formula can be rewritten as

Price-weighted index weight

which clearly shows that the weight of each asset in the index is its market price divided by the sum of the market prices of all assets.

Note that the divisor, which is equal to the number of shares, is typically adjusted for events such as stock splits and dividends. The divisor is used to ensure that the value of the index remains consistent over time despite changes in the number of outstanding shares. A more general formula may then be:

Index value

Where D is the divisor which is adjusted over time to account for events such as stock splits and dividends.

Use of the Nikkei 225 index in asset management

Asset managers have shifted their attention in recent years to including environmental, social, and governance (ESG) factors in their investment choices. A number of ESG-related initiatives, such as the development of an ESG index that tracks businesses with high ESG scores, have been introduced by the Nikkei 225 index. The Nikkei 225 index may also be used by asset managers as a component of a more comprehensive global asset allocation strategy. For example, they may use the index to gain exposure to the Asian equity markets while also investing in other regions such as Europe and the Americas. In addition, the Nikkei 225 index can also be used as a risk management tool. Asset managers can spot potential risks and take action to reduce them by comparing a portfolio’s performance to the index.

Benchmark for equity funds

Equity funds that invest in Japanese stocks frequently use the Nikkei 225 index as a benchmark. The index is used by investment managers and individual investors to assess and contrast the performance of their holdings of Japanese equities with the performance of the overall market. Japanese exchange-traded funds (ETFs) and other investment products that follow the Japanese equity market use the index as a benchmark as well. Additionally, derivatives like futures and options that enable investors to trade on the Japanese equity market are based on the Nikkei 225 index.

Financial products around the Nikkei 225 index

There are several financial products that track the performance of the Nikkei 225 index, allowing investors to gain exposure to the Japanese stock market.

Nikkei 225 ETFs are a popular way for investors to gain exposure to the Japanese equity market, as they offer a low-cost and convenient way to invest in a diversified basket of stocks. Some of the largest Nikkei 225 ETFs by assets under management include the iShares Nikkei 225 ETF (NKY), the Nomura Nikkei 225 ETF (1321), and the Daiwa ETF Nikkei 225 (1320).
There are also mutual funds and index funds that track the Nikkei 225 index. These funds typically have higher fees than ETFs but may offer different investment strategies or options for investors.
Certificates are structured products that allow investors to gain exposure to the Nikkei 225 index without actually owning the underlying assets.
Futures contracts based on the Nikkei 225 index are also available for investors who want to trade the index with leverage or for hedging purposes. These futures contracts trade on the Osaka Exchange, a subsidiary of the Japan Exchange Group.

Historical data for the Nikkei 225 index

How to get the data?

The Nikkei 225 index is the most common index used in finance, and historical data for the Nikkei 225 index can be easily downloaded from the internet.

For example, you can download data for the Nikkei 225 index from March 1, 1990 on Yahoo! Finance (the Yahoo! code for Nikkei 225 index is ^N225).

Source: Yahoo! Finance.

You can also download the same data from a Bloomberg terminal.

R program

The R program below written by Shengyu ZHENG allows you to download the data from Yahoo! Finance website and to compute summary statistics and risk measures about the Nikkei 225 index.

Data file

The R program that you can download above allows you to download the data for the Nikkei 225 index from the Yahoo! Finance website. The database starts on March 1, 1990. It also computes the returns (logarithmic returns) from closing prices.

Table 3 below represents the top of the data file for the Nikkei 225 index downloaded from the Yahoo! Finance website with the R program.

Table 3. Top of the data file for the Nikkei 225 index.
Top of the file for the Nikkei 225 index data
Source: computation by the author (data: Yahoo! Finance website).

Evolution of the Nikkei 225 index

Figure 1 below gives the evolution of the Nikkei 225 index from March 1, 1990 to December 30, 2022 on a daily basis.

Figure 1. Evolution of the Nikkei 225 index.

Source: computation by the author (data: Yahoo! Finance website).

Figure 2 below gives the evolution of the Nikkei 225 index returns from March 1, 1990 to December 30, 2022 on a daily basis.

Figure 2. Evolution of the Nikkei 225 index returns.

Source: computation by the author (data: Yahoo! Finance website).

Summary statistics for the Nikkei 225 index

The R program that you can download above also allows you to compute summary statistics about the returns of the Nikkei 225 index.

Table 4 below presents the following summary statistics estimated for the Nikkei 225 index:

The mean
The standard deviation (the squared root of the variance)
The skewness
The kurtosis.

The mean, the standard deviation / variance, the skewness, and the kurtosis refer to the first, second, third and fourth moments of statistical distribution of returns respectively.

Table 4. Summary statistics for the Nikkei 225 index.

Source: computation by the author (data: Yahoo! Finance website).

Statistical distribution of the Nikkei 225 index returns

Historical distribution

Figure 3 represents the historical distribution of the Nikkei 225 index daily returns for the period from March 1, 1990 to December 30, 2022.

Figure 3. Historical distribution of the Nikkei 225 index returns.

Source: computation by the author (data: Yahoo! Finance website).

Gaussian distribution

The Gaussian distribution (also called the normal distribution) is a parametric distribution with two parameters: the mean and the standard deviation of returns. We estimated these two parameters over the period from March 1, 1990 to December 30, 2022. The mean of daily returns is equal to 0.02% and the standard deviation of daily returns is equal to 1.37% (or equivalently 3.94% for the annual mean and 28.02% for the annual standard deviation as shown in Table 3 above).

Figure 4 below represents the Gaussian distribution of the Nikkei 225 index daily returns with parameters estimated over the period from March 1, 1990 to December 30, 2022.

Figure 4. Gaussian distribution of the Nikkei 225 index returns.
Gaussian distribution of the daily Nikkei 225 index returns
Source: computation by the author (data: Yahoo! Finance website).

Risk measures of the Nikkei 225 index returns

The R program that you can download above also allows you to compute risk measures about the returns of the Nikkei 225 index.

Table 5 below presents the following risk measures estimated for the Nikkei 225 index:

The long-term volatility (the unconditional standard deviation estimated over the entire period)
The short-term volatility (the standard deviation estimated over the last three months)
The Value at Risk (VaR) for the left tail (the 5% quantile of the historical distribution)
The Value at Risk (VaR) for the right tail (the 95% quantile of the historical distribution)
The Expected Shortfall (ES) for the left tail (the average loss over the 5% quantile of the historical distribution)
The Expected Shortfall (ES) for the right tail (the average loss over the 95% quantile of the historical distribution)
The Stress Value (SV) for the left tail (the 1% quantile of the tail distribution estimated with a Generalized Pareto distribution)
The Stress Value (SV) for the right tail (the 99% quantile of the tail distribution estimated with a Generalized Pareto distribution)

Table 5. Risk measures for the Nikkei 225 index.

Source: computation by the author (data: Yahoo! Finance website).

The volatility is a global measure of risk as it considers all the returns. The Value at Risk (VaR), Expected Shortfall (ES) and Stress Value (SV) are local measures of risk as they focus on the tails of the distribution. The study of the left tail is relevant for an investor holding a long position in the Nikkei 225 index while the study of the right tail is relevant for an investor holding a short position in the Nikkei 225 index.

Financial maps

You can find financial world maps on the Extreme Events in Finance website. These maps represent the performance, risk and extreme risk in international equity markets.

Figure 5 below represents the world map for extreme risk estimated by the extreme value distribution (see Longin (2016 and 2000)).

Figure 5. Extreme risk map.

Source: Extreme Events in Finance.

Why should I be interested in this post?

For a number of reasons, management students (as future managers and individual investors) should learn about the Nikkei 225 index. The Nikkei 225 index is a key benchmark for the Japanese equity market, which is one of the world’s largest market. Understanding how the index is constructed, how it performs, and the companies that make up the index is important for anyone studying finance or business in Japan or interested in investing in Japanese equities.

Individual investors can assess the performance of their own investments in the Japanese equity market with the Nikkei 225 index. Last but not least, a lot of asset management firms base their mutual funds and exchange-traded funds (ETFs) on the Nikkei 225 index which can considered as interesting assets to diversify a portfolio. Learning about these products and their portfolio and risk management applications can be valuable for management students.

Useful resources

Academic research about risk

Longin F. (2000) From VaR to stress testing: the extreme value approach Journal of Banking and Finance, N°24, pp 1097-1130.

Longin F. (2016) Extreme events in finance: a handbook of extreme value theory and its applications Wiley Editions.

Data

Yahoo! Finance

Yahoo! Finance Nikkei 225 index

Other

Extreme Events in Finance

Extreme Events in Finance Risk maps

Wikipedia Nikkei 225

About the author

The article was written in April 2023 by Nithisha CHALLA (ESSEC Business School, Grande Ecole Program – Master in Management, 2021-2023).

Extreme returns and tail modelling of the Nikkei 225 index for the Japanese equity market

The Nikkei 225 index for the Japanese equity market

Summary statistics for the Nikkei index

Modelling of the tails

Applications in risk management

Why should I be interested in this post?

Download R file to model extreme behavior of the index

Related posts on the SimTrade blog

About financial indexes

About portfolio management

About statistics

Useful resources

Academic resources

Other resources

About the author

The Nikkei 225 index

The Nikkei 225 index

Calculation of the Nikkei 225 index value

Use of the Nikkei 225 index in asset management

Benchmark for equity funds

Financial products around the Nikkei 225 index

Historical data for the Nikkei 225 index

How to get the data?

R program

Data file

Evolution of the Nikkei 225 index

Summary statistics for the Nikkei 225 index

Statistical distribution of the Nikkei 225 index returns

Historical distribution

Gaussian distribution

Risk measures of the Nikkei 225 index returns

Financial maps

Why should I be interested in this post?

Related posts on the SimTrade blog

About financial indexes

Other financial indexes

About portfolio management

About statistics

Useful resources

Academic research about risk

Data

Other

About the author