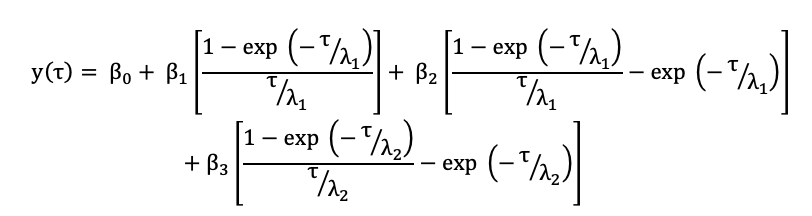Fixed-income arbitrage strategy

January 10, 2023 by Youssef LOURAOUI

Fixed-income arbitrage strategy

In this article, Youssef LOURAOUI (Bayes Business School, MSc. Energy, Trade & Finance, 2021-2022) presents the fixed-income arbitrage strategy which is a well-known strategy used by hedge funds. The objective of the fixed-income arbitrage strategy is to benefit from trends or disequilibrium in the prices of fixed-income securities using systematic and discretionary trading strategies.

This article is structured as follow: we introduce the fixed-income arbitrage strategy principle. Then, we present a practical case study to grasp the overall methodology of this strategy. We also present a performance analysis of this strategy and compare it a benchmark representing all hedge fund strategies (Credit Suisse Hedge Fund index) and a benchmark for the global equity market (MSCI All World Index).

Introduction

According to Credit Suisse (a financial institution publishing hedge fund indexes), a fixed-income arbitrage strategy can be defined as follows: “Fixed-income arbitrage funds attempt to generate profits by exploiting inefficiencies and price anomalies between related fixed-income securities. Funds limit volatility by hedging out exposure to the market and interest rate risk. Strategies include leveraging long and short positions in similar fixed-income securities that are related either mathematically or economically. The sector includes credit yield curve relative value trading involving interest rate swaps, government securities and futures, volatility trading involving options, and mortgage-backed securities arbitrage (the mortgage-backed market is primarily US-based and over-the-counter)”.

Types of arbitrage

Fixed-income arbitrage makes money based on two main underlying concepts:

Pure arbitrage

Identical instruments should have identical price (this is the law of one price). This could be the case, for instance, of two futures contracts traded on two different exchanges. This mispricing could be used by going long the undervalued contract and short the overvalued contract. This strategy uses to work in the days before the rise of electronic trading. Now, pure arbitrage is much less obvious as information is accessible instantly and algorithmic trading wipe out this kind of market anomalies.

Relative value arbitrage

Similar instruments should have a similar price. The fundamental rationale of this type of arbitrage is the notion of reversion to the long-term mean (or normal relative valuations).

Factors that influence fixed-income arbitrage strategies

We list below the sources of market inefficiencies that fixed-income arbitrage funds can exploit.

Market segmentation

Segmentation is of concern for fixed-income arbitrageurs. In financial institutions, the fixed-income desk is split into different traders looking at specific parts of the yield curve. In this instance, some will focus on very short, dated bonds, others while concentrate in the middle part of the yield curve (2-5y) while other while be looking at the long-end of the yield curve (10-30y).

Regulation

Regulation has an implication in the kind of fixed-income securities a fund can hold in their books. Some legislations regulate actively to have specific exposure to high yield securities (junk bonds) since their probability of default is much more important. The diminished popularity linked to the tight regulation can make the valuation of those bonds more attractive than owning investment grade bonds.

Liquidity

Liquidity is also an important concern for this type of strategy. The more liquid the market, the easier it is to trade and execute the strategy (vice versa).

Volatility

Large market movements in the market can have implications to the profitability of this kind of strategy.

Instrument complexity

Instrument complexity can also be a reason to have fixed-income securities. The events of 2008 are a clear example of how banks and regulators didn’t manage to price correctly the complex instruments sold in the market which were highly risky.

Application of a fixed-income arbitrage

Fixed-income arbitrage strategy makes money by focusing on the liquidity and volatility factors generating risk premia. The strategy can potentially generate returns in both rising and falling markets. However, understanding the yield curve structure of interest rates and detecting the relative valuation differential between fixed-income securities is the key concern since this is what makes this strategy profitable (or not!).

We present below a case study related tot eh behavior of the yield curves in the European fixed-income markets inn the mid 1990’s

The European yield curve differential during in the mid 1990’s

The case showed in this example is the relative-value trade between Germany and Italian yields during the period before the adoption of the Euro as a common currency (at the end of the 1990s). The yield curve should reflect the future path of interest rates. The Maastricht treaty (signed on 7th February 1992) obliged most EU member states to adopt the Euro if certain monetary and budgetary conditions were met. This would imply that the future path of interest rates for Germany and Italy should converge towards the same values. However, the differential in terms of interest rates at that point was nearly 350 bps from 5-year maturity onwards (3.5% spread) as shown in Figure 1.

Figure 1. German and Italian yield curve in January 1995.

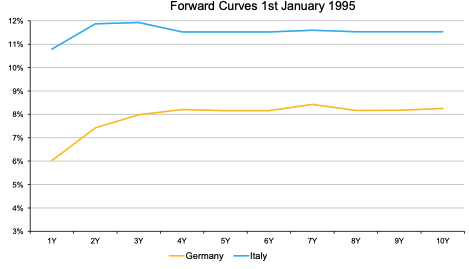
Source: Motson (2022) (Data: Bloomberg).

A fixed-income arbitrageur could have profited by entering in an interest rate swap where the investor receives 5y-5y forward Italian rates and pays 5y-5y German rates. If the Euro is introduced, then the spread between the two yield curves for the 5-10y part should converge to zero. As captured in Figure 2, the rates converged towards the same value in 1998, where the spread between the two rates converged to zero.

Figure 2. Payoff of the fixed-income arbitrage strategy.

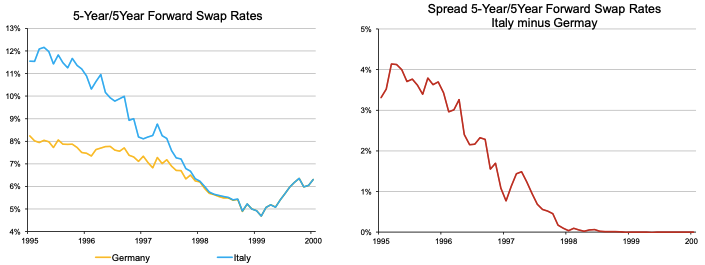
Source: Motson (2022) (Data: Bloomberg).

Performance of the fixed-income arbitrage strategy

Overall, the performance of the fixed-income arbitrage between 1994-2020 were smaller on scale, with occasional large drawdowns (Asian crisis 1998, Great Financial Crisis of 2008, Covid-19 pandemic 2020). This strategy is skewed towards small positive returns but with important tail-risk (heavy losses) according to Credit Suisse (2022). To capture the performance of the fixed-income arbitrage strategy, we use the Credit Suisse hedge fund strategy index. To establish a comparison between the performance of the global equity market and the fixed-income arbitrage strategy, we examine the rebased performance of the Credit Suisse index with respect to the MSCI All-World Index.

Over a period from 2002 to 2022, the fixed-income arbitrage strategy index managed to generate an annualized return of 3.81% with an annualized volatility of 5.84%, leading to a Sharpe ratio of 0.129. Over the same period, the Credit Suisse Hedge Fund index Index managed to generate an annualized return of 5.04% with an annualized volatility of 5.64%, leading to a Sharpe ratio of 0.197. The results are in line with the idea of global diversification and decorrelation of returns derived from the global macro strategy from global equity returns. Overall, the Credit Suisse fixed-income arbitrage strategy index performed better than the MSCI All World Index, leading to a higher Sharpe ratio (0.129 vs 0.08).

Figure 3 gives the performance of the fixed-income arbitrage funds (Credit Suisse Fixed-income Arbitrage Index) compared to the hedge funds (Credit Suisse Hedge Fund index) and the world equity funds (MSCI All-World Index) for the period from July 2002 to April 2021.

Figure 3. Performance of the fixed-income arbitrage strategy.
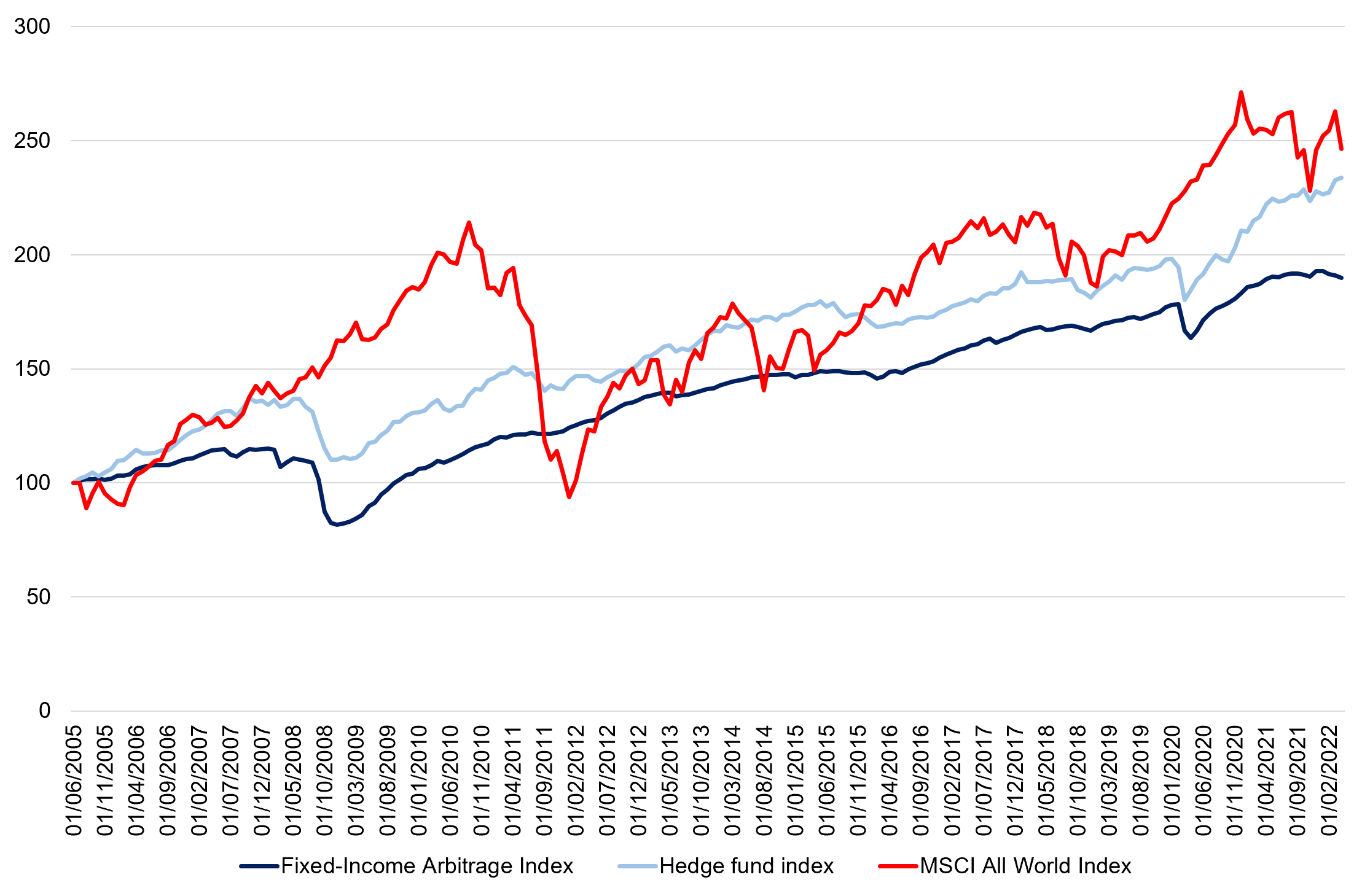
Global macro performance
Source: computation by the author (Data: Bloomberg).

You can find below the Excel spreadsheet that complements the explanations about the fixed-income arbitrage strategy.

Why should I be interested in this post?

The fixed-income arbitrage strategy aims to profit from market dislocations in the fixed-income market. This can be implemented, for instance, by investing in inexpensive fixed-income securities that the fund manager predicts that it will increase in value, while simultaneously shorting overvalued fixed-income securities to mitigate losses. Understanding the profits and risks associated with such a strategy may aid investors in adopting this hedge fund strategy into their portfolio allocation.

Useful resources

Academic research

Pedersen, L. H., 2015. Efficiently Inefficient: How Smart Money Invests and Market Prices Are Determined. Princeton University Press.

Motson, N. 2022. Hedge fund elective. Bayes (formerly Cass) Business School.

Business Analysis

Credit Suisse Hedge fund strategy

Credit Suisse Hedge fund performance

Credit Suisse Fixed-income arbitrage strategy

Credit Suisse Fixed-income arbitrage performance benchmark

About the author

The article was written in January 2023 by Youssef LOURAOUI (Bayes Business School, MSc. Energy, Trade & Finance, 2021-2022).

Interest rate term structure and yield curve calibration

January 9, 2023 by Youssef LOURAOUI

Interest rate term structure and yield curve calibration

In this article, Youssef LOURAOUI (Bayes Business School,, MSc. Energy, Trade & Finance, 2021-2022) presents the usage of a widely used model for building the yield curve, namely the Nelson-Seigel-Svensson model for interest rate calibration.

This article is structured as follows: we introduce the concept of the yield curve. Next, we present the mathematical foundations of the Nelson-Siegel-Svensson model. Finally, we illustrate the model with practical examples.

Introduction

Fine-tuning the term structure of interest rates is the cornerstone of a well-functioning financial market. For this reason, the testing of various term-structure estimation and forecasting models is an important topic in finance that has received considerable attention for several decades (Lorenčič, 2016).

The yield curve is a graphical representation of the term structure of interest rates (i.e. the relationship between the yield and the corresponding maturity of zero-coupon bonds issued by governments). The term structure of interest rates contains information on the yields of zero-coupon bonds of different maturities at a certain date (Lorenčič, 2016). The construction of the term structure is not a simple task due to the scarcity of zero-coupon bonds in the market, which are the basic elements to estimate the term structure. The majority of bonds traded in the market carry coupons (regular paiement of interests). The yields to maturity of coupon bonds with different maturities or coupons are not immediately comparable. Therefore, a method of measuring the term structure of interest rates is needed: zero-coupon interest rates (i.e. yields on bonds that do not pay coupons) should be estimated from the prices of coupon bonds of different maturities using interpolation methods, such as polynomial splines (e.g. cubic splines) and parsimonious functions (e.g. Nelson-Siegel).

As explained in an interesting paper that I read (Lorenčič, 2016), the prediction of the term structure of interest rates is a basic requirement for managing investment portfolios, valuing financial assets and their derivatives, calculating risk measures, valuing capital goods, managing pension funds, formulating economic policy, making decisions about household finances, and managing fixed income assets . The pricing of fixed income securities such as swaps, bonds and mortgage-backed securities depends on the yield curve. When considered together, the yields of non-defaulting government bonds with different characteristics reveal information about forward rates, which are potentially predictive of real economic activity and are therefore of interest to policy makers, market participants and economists. For instance, forward rates are often used in pricing models and can indicate market expectations of future inflation rates and currency appreciation/depreciation rates. Understanding the relationship between interest rates and the maturity of securities is a prerequisite for developing and testing the financial theory of monetary and financial economics. The accurate adjustment of the term structure of interest rates is the backbone of a well-functioning financial market, which is why the refinement of yield curve modelling and forecasting methods is an important topic in finance that has received considerable attention for several decades (Lorenčič, 2016).

The most commonly used models for estimating the zero-coupon curve are the Nelson-Siegel and cubic spline models. For example, the central banks of Belgium, Finland, France, Germany, Italy, Norway, Spain and Switzerland use the Nelson-Siegel model or a type of its improved extension to fit and forecast yield curves (BIS, 2005). The European Central Bank uses the Sonderlind-Svensson model, an extension of the Nelson-Siegel model, to estimate yield curves in the euro area (Coroneo, Nyholm & Vidova-Koleva, 2011).

Mathematical foundation of the Nelson-Siegel-Svensson model

In this article, we will deal with the Nelson-Siegel extended model, also known as the Nelson-Siegel-Svensson model. These models are relatively efficient in capturing the general shapes of the yield curve, which explains why they are widely used by central banks and market practitioners.

Mathematically, the formula of Nelson-Siegel-Svensson is given by:

img_SimTrade_NSS_equation

where

τ = time to maturity of a bond (in years)
β₀ = parameter to capture for the level factor
β₁= parameter to capture the slope factor
β₂ = parameter to capture the curvature factor
β₃ = parameter to capture the magnitude of the second hump
λ₁ and λ₂ = parameters to capture the rate of exponential decay
exp = the mathematical exponential function

The parameters β₀, β₁, β₂, β₃, λ₁ and λ₂ can be calculated with the Excel add-in “Solver” by minimizing the sum of squared residuals between the dirty price (market value, present value) of the bonds and the model price of the bonds. The dirty price is a sum of the clean price, retrieved from Bloomberg, and accrued interest. Financial research propose that the Svensson model should be favored over the Nelson-Siegel model because the yield curve slopes down at the very long end, necessitating the second curvature component of the Svensson model to represent a second hump at longer maturities (Wahlstrøm, Paraschiv, and Schürle, 2022).

Application of the yield curve structure

In financial markets, yield curve structure is of the utmost importance, and it is an essential market indicator for central banks. During my last internship at the Central Bank of Morocco, I worked in the middle office, which is responsible for evaluating risk exposures and profits and losses on the positions taken by the bank on a 27.4 billion euro foreign reserve investment portfolio. Volatility evaluated by the standard deviation, mathematically defined as the deviation of a random variable (asset prices or returns in my example) from its expected value, is one of the primary risk exposure measurements. The standard deviation reveals the degree to which the present return deviates from the expected return. When analyzing the risk of an investment, it is one of the most used indicators employed by investors. Among other important exposures metrics, there is the VaR (Value at Risk) with a 99% confidence level and a 95% confidence level for 1-day and 30-day positions. In other words, the VaR is a metric used to calculate the maximum loss that a portfolio may sustain with a certain degree of confidence and time horizon.

Every day, the Head of the Middle Office arranges a general meeting in which he discusses a global debriefing of the most significant overnight financial news and a debriefing of the middle office desk for “watch out” assets that may present an investment opportunity. Consequently, the team is tasked with adhering to the investment decisions that define the firm, as it neither operates as an investment bank nor as a hedge fund in terms of risk and leverage. As the central bank is tasked with the unique responsibility of safeguarding the national reserve and determining the optimal mix of low-risk assets to invest in, it seeks a good asset strategy (AAA bonds from European countries coupled with American treasury bonds). The investment mechanism is comprised of the segmentation of the entire portfolio into three principal tranches, each with its own features. The first tranche (also known as the security tranche) is determined by calculating the national need for a currency that must be kept safe in order to establish exchange market stability (mostly based on short-term positions in low-risk profile assets) (Liquid and high rated bonds). The second tranche is based on a buy-and-hold strategy and a market approach. The first entails taking a long position on riskier assets than the first tranche until maturity, with no sales during the asset’s lifetime (riskier bonds and gold). The second strategy is based on the purchase and sale of liquid assets with the expectation of better returns.

Participants in the market are accustomed to categorizing the debt of eurozone nations. Germany and the Netherlands, for instance, are regarded as “core” nations, and their debt as safe-haven assets (Figure 1). Due to the stability of their yield spreads, France, Belgium, Austria, Ireland, and Finland are “semi-core” nations (Figure 1). Due to their higher bond yields and more volatile spreads, Spain, Portugal, Italy, and Greece are called “peripheral” (BNP Paribas, 2019) (Figure 2). The 10-year gap represents the difference between a country’s 10-year bond yield and the yield on the German benchmark bond. It is a sign of risk. Therefore, the greater the spread, the greater the risk. Figure 3 represents the yield curve for the Moroccan bond market.

Figure 1. Yield curves for core countries (Germany, Netherlands) and semi-core (France, Austria) of the euro zone.

Source: computation by the author.

Figure 2. Yield curves for peripheral countries of the euro zone
(Spain, Italy, Greece and Portugal).
Yield curves for semi-core countries of the euro zone
Source: computation by the author.

Figure 3. Yield curve for Morocco.

Source: computation by the author.

This example provides a tool comparable to the one utilized by central banks to measure the change in the yield curve. It is an intuitive and simplified model created in an Excel spreadsheet that facilitates comprehension of the investment process. Indeed, it is capable of continuously refreshing the data by importing the most recent quotations (in this case, retrieved from investing.com, a reputable data source).

One observation can be made about the calibration limits of the Nelson-Seigel-Svensson model. In this sense, when the interest rate curve is in negative levels (as in the case of the structure of the Japanese curve), the NSS model does not manage to model negative values, obtaining a result with substantial deviations from spot rates. This can be interpreted as a failure of the NSS calibration approach to model a negative interest rate curve.

In conclusion, the NSS model is considered as one of the most used and preferred models by central banks to obtain the short- and long-term interest rate structure. Nevertheless, this model does not allow to model the structure of the curve for negative interest rates.

Excel file for the calibration model of the yield curve

You can download an Excel file with data to calibrate the yield curve for different countries. This spreadsheet has a special macro to extract the latest data pulled from investing.com website, a reliable source for time-series data.

Why should I be interested in this post?

Predicting the term structure of interest rates is essential for managing investment portfolios, valuing financial assets and their derivatives, calculating risk measures, valuing capital goods, managing pension funds, formulating economic policy, deciding on household finances, and managing fixed income assets. The yield curve affects the pricing of fixed income assets such as swaps, bonds, and mortgage-backed securities. Understanding the yield curve and its utility for the markets can aid in comprehending this parameter’s broader implications for the economy as a whole.

Useful resources

Academic research

Lorenčič, E., 2016. Testing the Performance of Cubic Splines and Nelson-Siegel Model for Estimating the Zero-coupon Yield Curve. NGOE, 62(2), 42-50.

Wahlstrøm, Paraschiv, and Schürle, 2022. A Comparative Analysis of Parsimonious Yield Curve Models with Focus on the Nelson-Siegel, Svensson and Bliss Versions. Springer Link, Computational Economics, 59, 967–1004.

Business Analysis

BNP Paribas (2019) Peripheral Debt Offers Selective Opportunities

About the author

The article was written in January 2023 by Youssef LOURAOUI (Bayes Business School,, MSc. Energy, Trade & Finance, 2021-2022).