Understanding Options and Options Trading Strategies

December 13, 2021 by Luis RAMIREZ

Understanding Options and Options Trading Strategies

In this article, Luis RAMIREZ (ESSEC Business School, Global BBA, 2019-2023) discusses the fundamentals behind options trading.

Financial derivatives

In order to understand and grasp the concept of options, knowledge of what is a derivative should be established. A financial instrument derivative is ultimately an instrument whose value derives from the value of an underlying asset (or multiple underlying assets). These underlying assets can of course be bonds, stocks, commodities, currencies, etc. Derivatives are widely common and used around the world; investment banks, commercial banks, and corporations (mainly multinational corporations) are all consistent users of derivatives. The purpose, or goal, behind derivatives is to manage risk, whether that be alleviating risk by hedging investments, or by taking on risk through speculative investments. To carry out this process, the investor must undertake one of the four types of derivatives. The four types are the following: options, forwards, futures, and swaps. In this article the focus will be solely placed on options.

What are options?

An option contract provides an investor the chance to either buy (for a call option) or sell (for a put option) the underlying asset, depending on what type of option they possess. Every option contract has an expiry date in which the investor can effectively exercise the option. A very important thing about options is that they provide investors the right, but not the obligation, to either buy or sell an asset (i.e., stock shares) at a price and at a date that have been agreed at the issuing of the cotnract.

Put options vs call options

Firstly, the main two different options are call and put options. Call options give investors (that bought the call option) the right to buy a stock at a certain price and at a certain date, and put options give investors (that bought the put option) the right to sell a stock at a certain price and at a certain date. The first step into acquiring options, either type, is paying a premium. This premium which is spent at the beginning of the process is the only loss that investors will face if the options are not exercised. However, the other side of the coin, options writers (sellers) are more exposed to risk as they are exposed to lose more than only the premium.

Sell-side vs buy-side

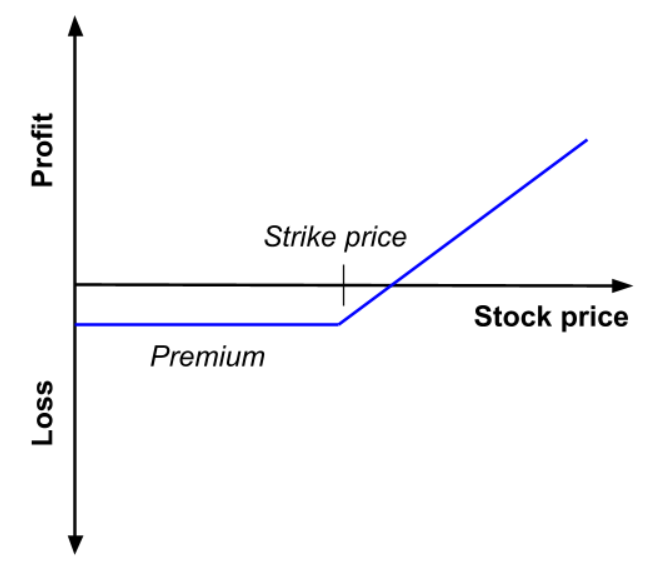
In an option contract, the price at which the asset is sold or bought is known as the strike price, or exercise price. When a call option has been bought, and the price of the share has
had a bullish trend and rises above the strike price, the investor can simply exercise his right to buy the share at the strike price, and then immediately sell it at the spot price, resulting in immediate profit. However, if the price of the share had a bearish trend and dropped below the strike price, the investor can decide not to exercise his right and will only lose the amount of premium paid in this case.

Figure 1. Profit and loss (P&L) of a long position in a call option
as a function of the price of the underlying asset at maturity
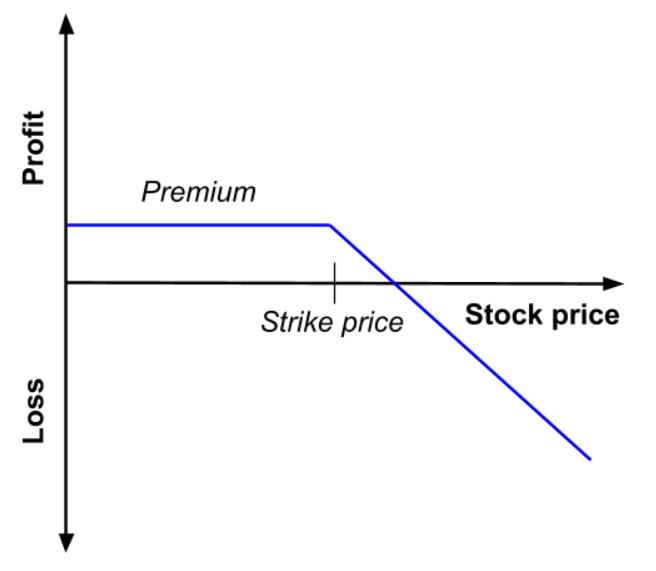
Profit and loss (P&L) as a function of the price of the underlying asset at maturity

Profit and loss (P&L) as a function of the price of the underlying asset at maturity

Source: production by the author.

On the other hand, selling options differs. Selling options is commonly known as writing options. The way this works is that a writer receives the premium from a buyer, this is the maximum profit a writer can receive by selling call options. Normally, a call option writer is bearish, therefore he believes that the price of the stack will fall below that of the strike price. If indeed the share price falls below the strike price, the writer would profit the premium paid by the buyer, since the buyer would not exercise the option. However, if the share price surpassed the strike price, the writer would have to sell shares at the low strike price. The writer would then experience a loss, the size of the loss depends on how many shares and price the writer would have to use to cover the entire option contract. Clearly, the risk for call writers is much higher than the risk exposure call buyers when acquiring an option. To summarize, the call buyer can only lose the premium paid, and the call writer can face infinite risk because the price of a share can keep increasing.

Figure 2. Profit and loss (P&L) of a short position in a call option
as a function of the price of the underlying asset at maturity
Profit and loss (P&L) as a function of the price of the underlying asset at maturity

Source: production by the author.

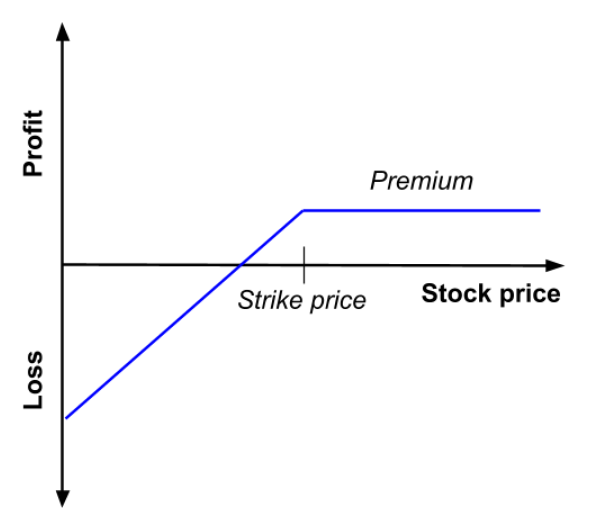
As for put options, put buyers usually believe the share price will decrease under the strike price. If this does eventually happen, the investor can simply exercise the put and sell at strike price, instead of a lower spot price. If the investor wants to go long, he can substitute the shares used in the option contract and buy them for a cheaper spot price after the put has been exercised. However, if the spot price is above the strike price, and the investor choses to not exercise the put, the loss will once again only be the cost of the premium.

Figure 3. Profit and loss (P&L) of a long position in a put option
as a function of the price of the underlying asset at maturity
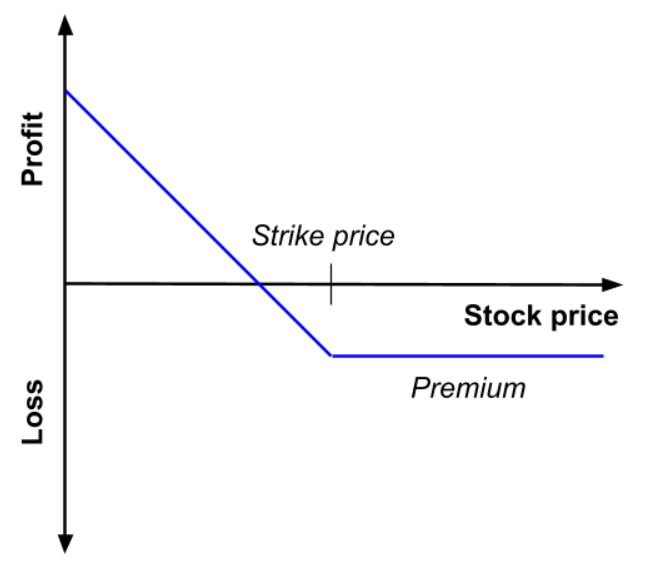
Profit and loss (P&L) as a function of the price of the underlying asset at maturity

Source: production by the author.

On the other hand, put writers think the share price will have a bullish trend throughout the duration of the option lifecycle. If the share price rises above strike price, the contract will expire, and the seller’s profit is the premium he received. If the share price decreases, and falls under the strike price, then the writer is obliged to buy shares at a strike price which higher than the spot price. This is when the risk is at the highest for a put writer, if the share price falls. Just like call writing, the loss can be hefty. Only that in the case of put writing, it happens if the share price tumbles down.

Figure 4. Profit and loss (P&L) of a short position in a put option
as a function of the price of the underlying asset at maturity
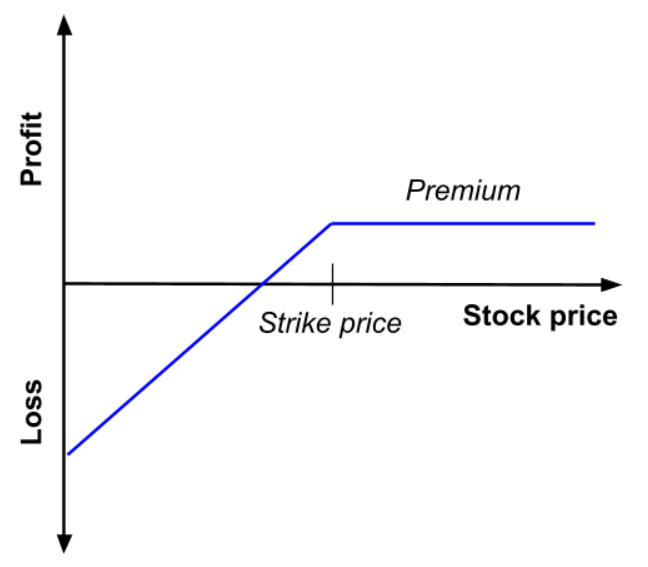
Profit and loss (P&L) as a function of the price of the underlying asset at maturity

Source: production by the author.

This can be shrunk down to knowing that call buyers can benefit from buying securities or assets at a lower price if the share price rises during the length of the option contract. Put buyers can benefit from selling assets at a higher strike price if the share price falls during the length of the option contract. As per writers, they receive a premium fee when writing options. However, it is not all positive points, option buyers need to pay the premium fee and discount this from their potential profit, and writers face an indefinite risk subject to the share price and quantity.

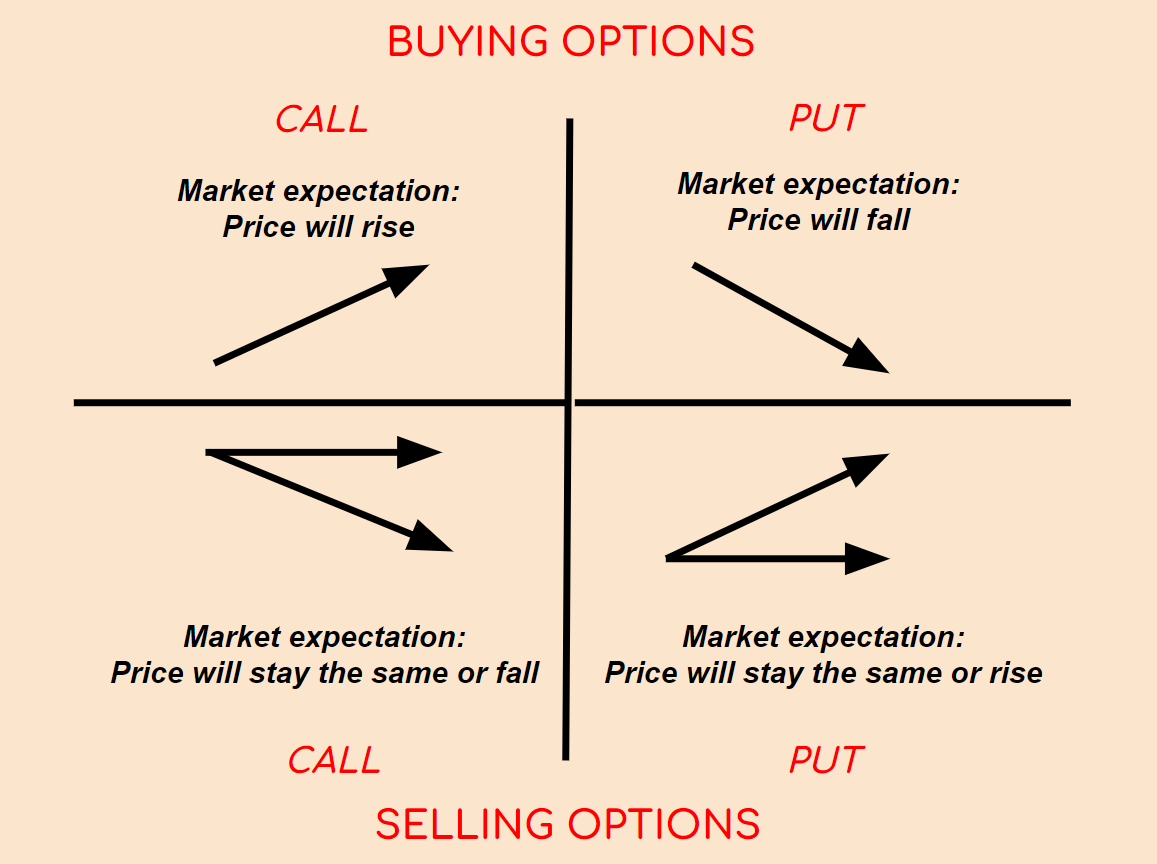
Figure 5. Market scenarios for buying and selling call and put options

Source: production by the author.

Option Trading Strategies

Four trading strategies have already been mentioned, selling or buying either puts or calls. However, there are several different option trading strategies and new ones are being produced frequently, anyhow the article will focus on five trading strategies that most, if not all, investors are familiar with.

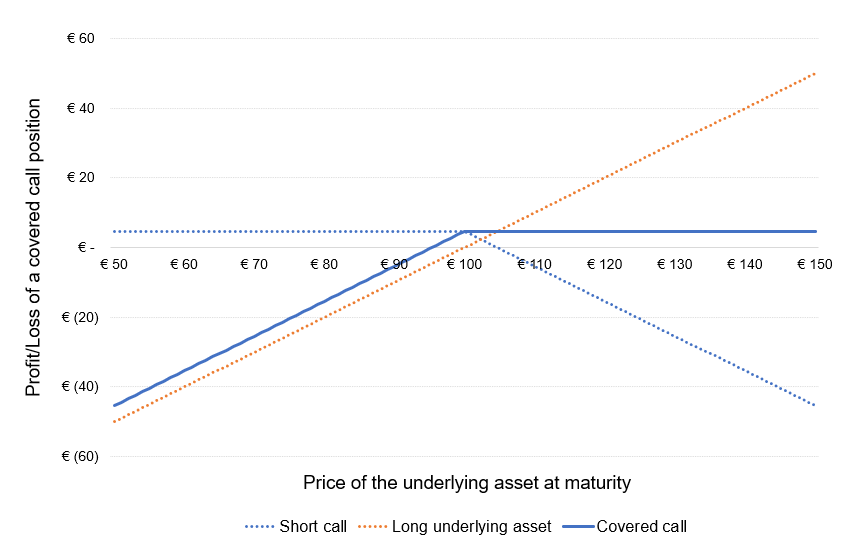
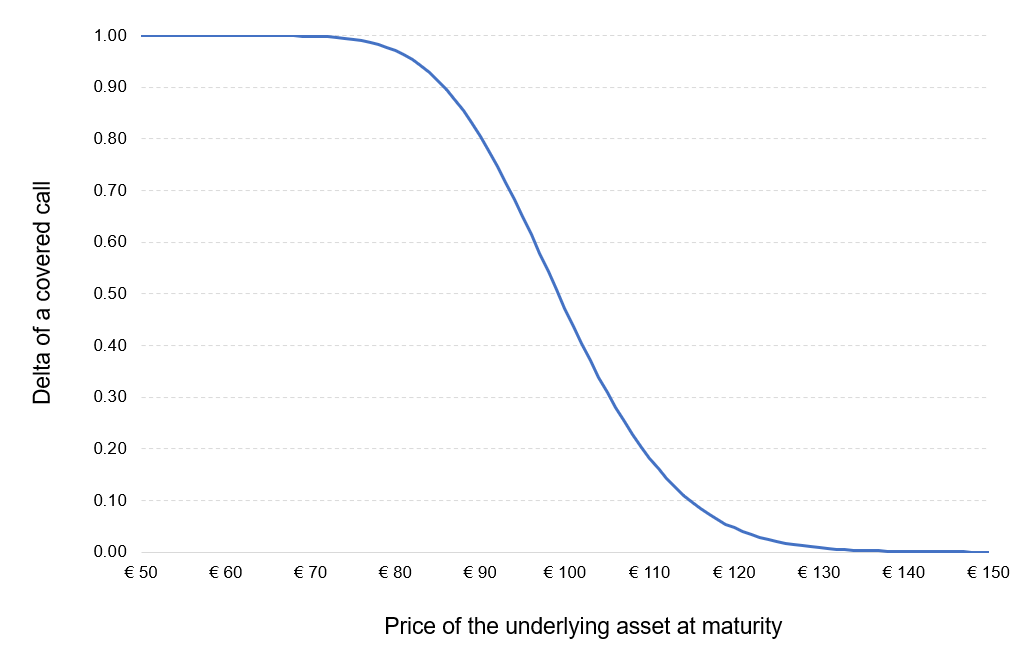
Covered Call

This trading strategy consists in the writer selling call options against the stock that he already owns. It is ‘covered’ because it covers the writer when the buyer of the option exercises his right to buy the shares, due to the writer already owning them, meaning that the writer can deliver the shares. This strategy is often used as an income stream from premiums. This is an employable strategy for those who believe that the asset they own will only experience a small change in price. The covered call is considered a low-risk strategy, and if used appropriately with a reliable stock, it can be a source of income.

Figure 6. Profit and loss (P&L) of a covered call
as a function of the price of the underlying asset at maturity

Source: production by the author.

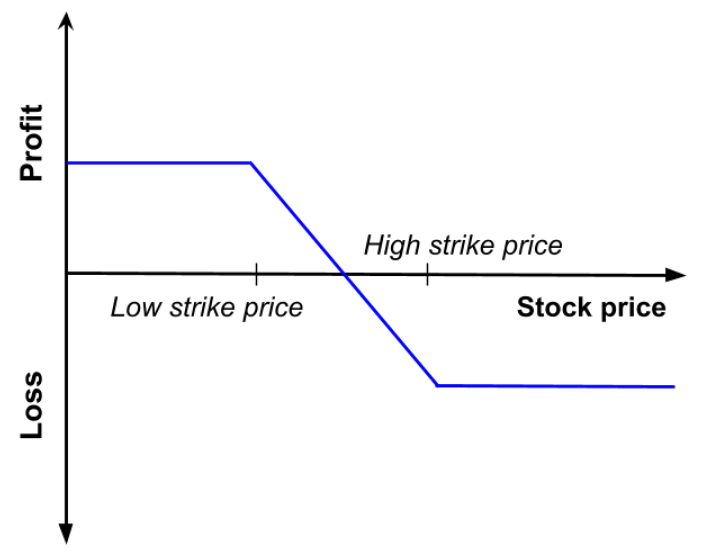
Married put

Like a covered call, in a married put the investor buys an asset and then buys a put option with the strike price being equal to the spot price. This is done to be protected against a decrease in the asset price. Of course, when buying an option, a premium must be paid, which is a downside for a married put strategy. However, the married put limits the loss an investor could incur in case of a price decrease. On the other hand, if the price increases, profit is unlimited. This strategy is often used for volatile stocks.

Figure 7. Profit and loss (P&L) of a married put
as a function of the price of the underlying asset at maturity

Source: production by the author.

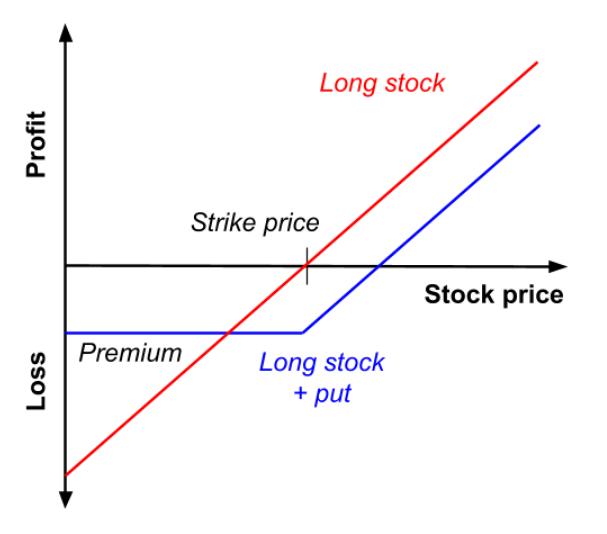
Protective Collar

This strategy is done when an investor buys a put option where the strike price is lower than the spot price, as well as instantly writing a call option where the strike price is higher than the spot price, this must be done by the investor owning said asset. This strategy protects the investor from a decrease in price. If the share price increases, large profits will be capped, however large losses will be also capped. When performing a protective collar, the best possibility for an investor is that the share price rises to the call strike price.

Figure 8. Profit and loss (P&L) of a protective collar
as a function of the price of the underlying asset at maturity

Source: production by the author.

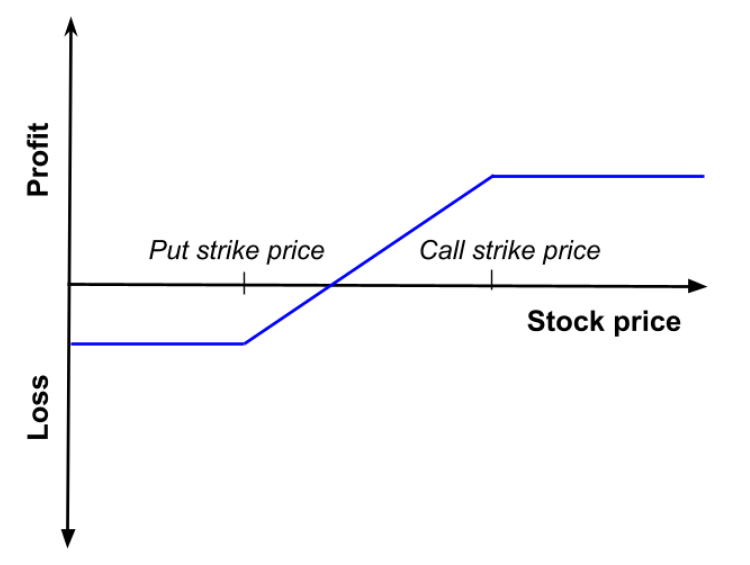
Bull Call Spread

In order to execute this strategy, an investor buys calls at the same time that he sells the equivalent order of calls, which have a higher strike price. Of course, both calls must be tied to the same asset. As seen on the name of this strategy, it is a strategy that an investor employs when he predicts a bullish trend. Just like the protective collar, it limits both, gains and losses.

Figure 9. Profit and loss (P&L) of a bull call spread
as a function of the price of the underlying asset at maturity

Source: production by the author.

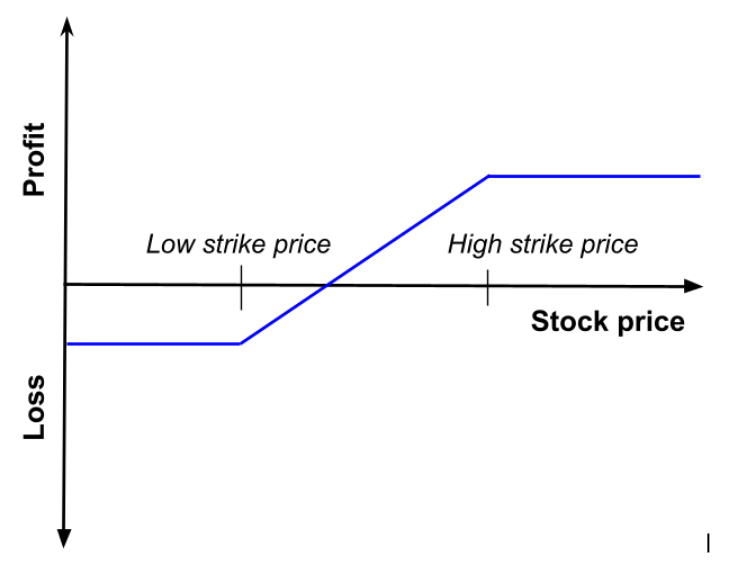
Bear Put Spread

This strategy is like the Bull Call Spread, only that it is in terms of a put option. The investor buys put options while he sells put options at a lower strike price. This can be done when the investor foresees a bearish trend, just like its call counterpart, the Bear Put Spread limits losses and gains.

Figure 10. Profit and loss (P&L) of a bear put spread
as a function of the price of the underlying asset at maturity

Source: production by the author.

Importance of options on financial markets

As seen on the variety of option trading strategies, and the different factors that play into each strategy mentioned, and dozens of other out there to explore, this instrument is a very utilized tool for investors, and financial institutions. The ‘options within options’ are of a huge variety and so much could be done. Many people have strong feelings towards this derivative, whether it is a negative, or positive stance, it all depends on the profits it brings. There is a lot of work behind options, and just like any other investment, due diligence is a key aspect of the procedure.

Useful Resources

Hull J.C. (2015) Options, Futures, and Other Derivatives, Ninth Edition.

Prof. Longin’s website Pricer d’options standards sur actions – Calls et puts (in French)

About the author

Article written in December 2021 by Luis RAMIREZ (ESSEC Business School, Global BBA, 2019-2023).

Covered call

December 11, 2021 by Akshit GUPTA

Covered Call

This article written by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) presents the concept of covered call used in equities option contracts.

Introduction

Hedging is a strategy implemented by investors to reduce the risk in an existing investment. In financial markets, hedging is an effective tool used by investors to minimize the risk exposure and change the risk profile for any investment in securities. While hedging does not necessarily eliminate the entire risk for any investment, it does limit the potential losses that the investor can incur.

Option contracts are commonly used by market participants (traders, investors, asset managers, etc.) as hedging mechanisms due to their great flexibility (in terms of expiration date, moneyness, liquidity, etc.) and availability. Positions in options are used to offset the risk exposure in the underlying security, another option contract or in any other derivative contract. There are various popular strategies that can be implemented through option contracts to minimize risk and maximize returns, one of which is a covered call.

Covered call

The covered call strategy is a two-part strategy that essentially involves an investor writing a call option on an underlying security while simultaneously holding a long position in the same underlying. This action of buying an asset and writing calls on it at the same time is commonly referred as ‘buy write’. By writing a call option, the investor locks in the price of the underlying asset, thereby enjoying a short-term gain from the premium received.

Market scenario

The covered call is generally ideal if the investor has a neutral or slightly bullish outlook of the market wherein the potential future upside of the underlying asset owned by the investor is limited. This strategy is used by investors when they would prefer booking short-term profits on the assets than to keep holding it.

For instance, consider a ‘buy write’ situation where an investor buys shares of a stock (i.e., holds a long position in the stock) and simultaneously writes call options on them. The investor has a neutral view on the stock and doesn’t expect the price to rise much.
To book a short-term profit and also hedge any minor downsides in the stock price, the investor is writing call options on the stock at a strike price greater than or equal to the current price of the stock (i.e. out-of-the-money or at-the-money call options). The buyer of those call options would pay the investor a premium on those calls, whether or not the option is exercised. This is the covered call strategy in a nutshell.

Let us consider a covered call position with writing at-the money calls. One of following three scenarios may happen:

Scenario 1: the stock price does not change, and calls expire at the money

In this scenario, the market viewpoint of the investor holds correct and the profit from the strategy is the premium earned on the call options. In this case, the option holder does not exercise its call options, and the investor gets to keep the underlying stocks too.

Scenario 2: the stock price rises, and calls expire in the money

In this scenario, since the price of the stock was already locked in through the call, the investor enjoys a short-term profit along with the premium. However, this also poses a risk in case the price of the stock rises substantially because the investor misses out on the opportunity.

Scenario 3: the stock price falls and calls expire out of the money

This is a negative scenario for the investor. There is limited protection from the downside through the premium earned on the call options. However, if the stock price falls below a certain break-even point, the losses for the investor can be considerable since there will be a fall in its underlying position.

Risk profile

In a covered call, the total cost of the investment is equal to the price of the underlying asset minus the premium earned by writing the call. However, the profit potential for the investment is limited and the maximum loss can be significantly high. The risk profile of the position is represented in Figure 1.

Figure 1. Risk profile of covered call position.

Source: computation by the author (based on the BSM model).

You can download below the Excel file for the computation of the Profit or Loss (P&L) function of the underlying position and covered call position.

The delta of the position is equal to the sum of the delta of the long position in the underlying asset (+1) and the short position in the call option (-Δ).

Figure 2 represents the delta of the covered call position as a function of the price of the underlying asset. The delta of the call option is computed with the Black-Scholes-Merton model (BSM model).

Figure 2. Delta of a covered call position.

Source: computation by the author (based on the BSM model).

You can download below the Excel file for the computation of the delta of a protective put position.

Example

An investor holds 100 shares of Apple bought at the current price of $144 each. The total investment is then equal to $14,400. She is neutral about the short-term prospects of the market. In order to gain from her market scenario, she decides to write an at-the-money call option at $144 on the Apple stock (lot size is 100) with a maturity of one month, using the covered call strategy.

We use the following market data: the current price of Appel stock is $144, the implied volatility of Apple stock is 22.79%, and the risk-free interest rate is equal to 1.59%.

Based on the Black-Scholes-Merton model, the price of the call option is $3.87.

Let us consider three scenarios at the time of maturity of the call option:

Scenario 1: stability of the price of the underlying asset at $144

The total cost of the initial investment is the cost of acquiring the Apple stocks ($14,400) minus the premium received on writing the calls ($387 = $3.87*100), which is equal to $14,013, i.e. $14,400 – $387.

As the stock price ($144) is equal to the strike price of the call options ($144), the value of the call options is equal to zero, and the investor earns a profit which is equal to the initial price of the call options (the premium), which is equal to $387.

Scenario 2: an increase in the price of the underlying asset to $155

The total cost of the initial investment is the cost of acquiring the Apple stocks ($14,400) minus the premium on writing the calls ($387 = $3.87*100), which is equal to $14,013, i.e. $14,400 – $387.

As the stock price has risen to $155, the call options are exercised by the option buyer, and the investor will have to sell the Apple stocks at the strike price of $144.

By executing the covered call strategy, the investor earns $387 (i.e. ($144-$144)*100 +$387) but misses the opportunity of earning higher profits by selling the stock at the current market price of $155.

Scenario 3: a decrease in the price of the underlying asset to $142

As the stock price is at $142, the call options are not exercised by the option buyer and the options expire worthless (out of the money).

As the buyer does not exercise the call options, the investor earns a profit which is equal to the price of the call options which is equal to $387. But his net profit decreases by the amount of the decrease in his position in the APPLE stocks which is equal to -$200 (i.e. ($142-$144)*100).

▶ All posts about Options

▶ Akshit GUPTA Options

▶ Akshit GUPTA Option Trader – Job description

▶ Akshit GUPTA The Black-Scholes-Merton model

▶ Akshit GUPTA Protective Put

▶ Akshit GUPTA Option Greeks – Delta

Useful Resources

Research articles

Black F. and M. Scholes (1973) “The Pricing of Options and Corporate Liabilities” The Journal of Political Economy, 81, 637-654.

Merton R.C. (1973) “Theory of Rational Option Pricing” Bell Journal of Economics, 4(1): 141–183.

Books

Hull J.C. (2015) Options, Futures, and Other Derivatives, Ninth Edition, Chapter 10 – Trading strategies involving Options, 276-295.

Wilmott P. (2007) Paul Wilmott Introduces Quantitative Finance, Second Edition, Chapter 8 – The Black Scholes Formula and The Greeks, 182-184.

About the author

Article written in December 2021 by Akshit GUPTA (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).