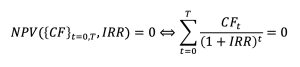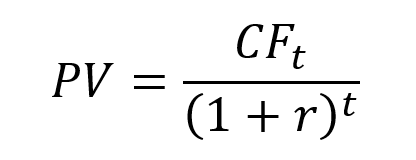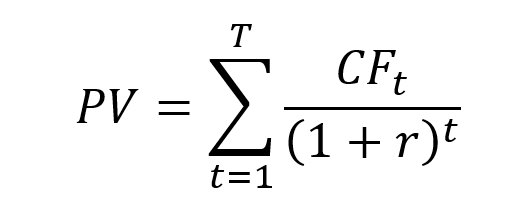How to compute the net present value of an investment in Excel

December 7, 2021 by Maite CARNICERO MARTINEZ

How to compute the net present value of an investment in Excel

In this article, Maite CARNICERO MARTINEZ (ESSEC Business School, Global Bachelor of Business Administration, 2021-2022, exchange student from the University of Salamanca) explains how to compute the net present value of an investment in Excel.

When the time comes that one must choose what project to embark on, there are several measures to compare the available options, such as the internal rate of return, the payback method and the net present value (also known as the “discounted cash flow” method or DCF). In this article, I will focus on the last one of these tools, which is the preferred by most financial analysts.

A project is a temporary, unique and progressive endeavor to produce a tangible or intangible result, for instance, a new product or a competitive advantage. It normally entails the execution of some tasks over a period of time, conditioned to limitations related to cost, quality or performance. During its implementation, an initial investment and a series of cash flows are to be generated at different times. Some examples of projects are: developing a new service, building a factory, and implementing a new process.

The Net Present Value (NPV) compares the present value of the future cash flows with the investment made at the beginning. The computation of the present value uses a the required rate of return. It takes into account the time value of money, translating future cash flows into today’s value, since the buying power of money today is greater that the buying power of the same amount in the future.

The NPV is the basis of the discounted cash flow model (DCF) which allows investors to compare the initial cash flow of expenditure against the present value of future cash flows. It could be used to evaluate whether an important investment is worthwhile, but also in mergers and acquisitions and to compare companies, like Warren Buffet does, because once we have calculated the different NPVs we will know which investment has the biggest gain.

To sum up, the NPV allows us to do evaluate investments from a financial point of view and select the best one.

Modelling of an investment

How can we calculate it?

The mathematical formula for the NPV is given by:

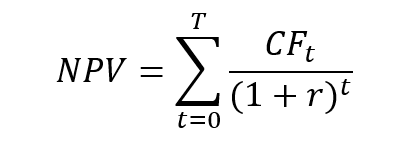
CF_t = cash flows of each period (from t=0 to t=T)
T = number of periods
r = discount rate or interested rate required of the investment. It is the rate of return that the investors expect on their investment

For a classical project, the first cash flow, CF₀, is negative and corresponds to the initial cost of the project and the following cash flows, CF_t for t=1 to t=T, are assumed to be positive. The NPV can be rewritten as

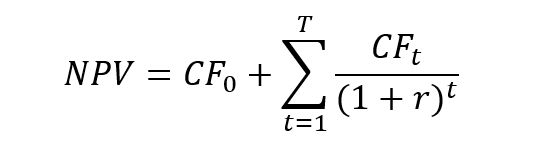
This formula clearly shows that the NPV compares the first cash flow on the one hand, and the present value of future cash flows on the other hand. As the initial cash flow is negative and the present value of future cash flows is positive, the sign of the NPV depends on relative weight of these two components.

Investment decision

The NPV can be used as a criterion for the investment decision.

If the NPV is positive, the investment should be made as it creates value.
If the NPV is zero, the investment should be made or not.
If the NPV is negative, the investment should not be made as it destroys value.

Advantages

The NPV of an investment is easy to calculate, specially nowadays with financial calculators and spreadsheets like Excel.
The NPV measures the effect of the investment on the firm’s value.
The NPV It takes into account the maturity of each cash flow.

Disadvantages

In order to compute the NPV, the discount rate has to be specified and it is a difficult issue.
The calculations are based on assumptions and estimations and the reality can differ from them.
Misestimations can be found in the initial investment, on the discount rate and on the projected returns of the project.
The NPV formula presumes that the cash flows are immediately reinvested at the same rate as the discount rate.
It presumes that the negative cash flows are financed with resources whose cost is also the discount rate.

How to compute the NPV on Excel?

Example

Excel is an extended tool in the financial world, also to calculate the NPV. Let’s take an example to illustrate how we can use it: we are offered a project in which we have to invest 42,000 euros and we will receive 8,400 euros the first year, 9,000 the second, 10,300 the third, 11,700 the fourth and 13,000 the last year.

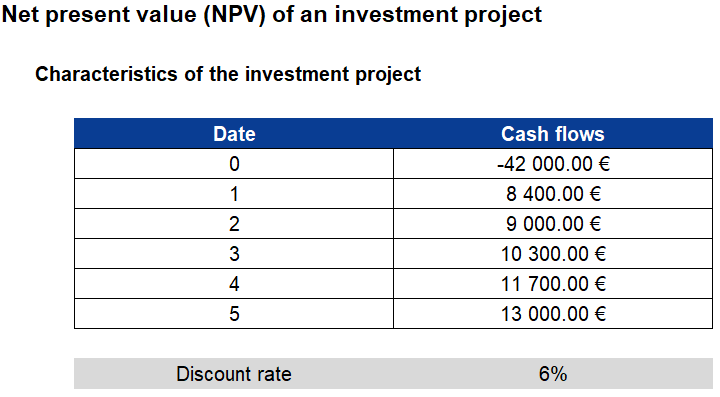
Assuming that the discount rate is 6% per year, what will be the NPV?

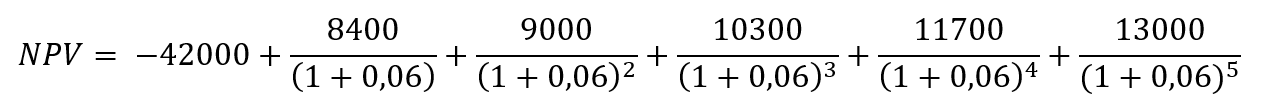
Hand-made computation

We can do a hand-made computation of the NPV:

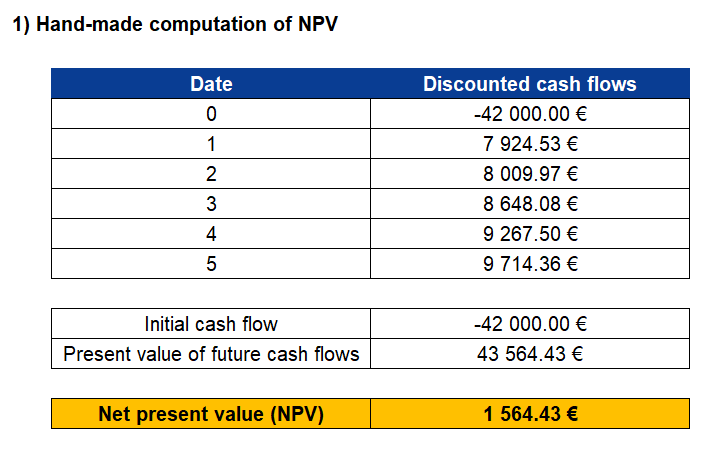
We find a NPV of €1,564.43. As the NPV of the investment is positive, we will take the project.

Computation with Excel

We can also use Excel to compute the NPV:

Useful resources

longin.fr website Cours Gestion financière (in French).

Mazars Excel IRR Function And Other Ways To Calculate IRR In Excel

Economipedia NPV definition (in Spanish)

HBR NPV use and calculation

HBR NPV limitations

MyManagementGuide Project definition

About the author

The article was written in December 2021 by Maite CARNICERO MARTINEZ (ESSEC Business School, Global Bachelor of Business Administration, 2021-2022, exchange student from the University of Salamanca).

The Internal Rate of Return

May 31, 2021 by Raphaël ROERO DE CORTANZE

The Internal Rate of Return

In this article, Raphaël ROERO DE CORTANZE (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022) explains the financial concept of internal rate of return (IRR).

What is the Internal Rate of Return?

The Internal Rate of Return (IRR or “TRI” – “taux de rendement interne” in French) of a sequence of cash flows is the discount rate that makes the Net Present Value (NPV or “VNP” or “VAN” for “valeur nette présente” or “valeur actuelle nette” in French) of this sequence of cash flows equal to zero.

Screenshot 2021-05-31 at 21.59.49

In order to calculate the IRR, two methods can be used. First of all, use the Excel “IRR” formula on the sequence of cash flows, which will automatically display an approximate value for the IRR. Nonetheless, if Excel is not available for performing the IRR calculation, you can use the dichotomy method (which is indeed used by Excel). The dichotomy method uses several iterations to determine an approximation of the IRR. The more iterations are performed, the more accurate the final IRR output is. For each iteration, the table below assesses whether the NPV using the “Average” discount rate is positive or negative. If it is negative (resp. positive), it means the IRR is somewhere in between the “Lower bound” (resp. “Upper bound” and the “Average”) and the next iteration will thus keep the same “Lower bound” (resp. use the “Average” as the new lower bound) and use the “Average” as the new “Upper bound” (resp. keep the same “Upper bound”). After 10 iterations, the table displays an IRR of 18,457%, which is an approximation to the nearest hundredth of the 18,450% IRR calculated with the Excel formula.

The IRR criterion

In the same way as the NPV, the IRR can be used to evaluate the financial performance of:
A tangible investment: the IRR criterion can be used to evaluate which investment project will be the most profitable. For instance, if a firm hesitating between Project A (buying a new machine), Project B (upgrading the existing machine) and Project C (outsourcing a fraction of the production), the firm can calculate the IRR of each project and compare them.
A financial investment: whether it is a bank investment or a private equity investment (purchase of a company) the IRR criterion can be used to sort different projects according to their financial performance.

Disaggregating the IRR

Investors and especially Private Equity firms often rely on the IRR as one measure of a project’s yield. Projects with the highest IRRs are considered the most attractive. The performance of Private Equity funds is also measured through the IRR criterion. In other words, PE firms use the IRR to select the most profitable projects and investors look at the IRR of PE funds when choosing to which PE firms’ fundraising campaign, they will participate in.

Nonetheless, IRR is the most important performance benchmark for PE investments, the IRR does not go into detail. Indeed, disaggregating the IRR can help better understand which are the different components of the IRR:

Unlevered IRR components:
- Baseline return: the cash flows that the acquired business was expected to generate without any improvements after acquisition.
- Business performance: value creation through growth by improving the business performance, margin increase and capital efficiency improvements.
- Strategic repositioning: value creation through by increasing the opportunity for future growth and returns (innovation, market entries etc.).
Leveraged IRR: PE investments heavily rely on high amounts or debt funding (hence the wide use of Leverage Buy-Out or LBO). Debt funding allows to resort to less equity funding, thus mechanically increasing the IRR of the investment.

Each of these components can have different proportions in the IRR. As an example, we can consider two PE funds A and B displaying the same IRR of 30%. After disaggregating each fund’s IRR, we come up with the following table, showing the weight of each IRR component in the total IRR (or “Levered IRR”). From this table, we understand that Fund A and Fund B have very different strategies. Fund A focuses in its PE operations on improving the business performance and carrying out strategic repositioning’s. Only 23% of the total IRR comes from financial engineering. In contrast, Fund B draws most of its performance from financial engineering, while only 23% of the total IRR comes from the unlevered IRR.

Through this example we understand that PE funds and firms can have very different strategies, while disclosing the same IRR. Thus, disaggregating the IRR can reveal the positioning of PE funds. Finally, disaggregating the IRR also allows to assess whether PE funds are true to the strategy they display: for instance, a fund can be specialized in strategic repositioning and business performance improvements on the paper, but drawing most of its value creation through financial engineering.

Useful resources

Prof. Longin’s website Calcul de la VNP et du TRI d’une séquence de flux (in French)

Prof. Longin’s website Méthode de dichotomie pour le calcul du TRI (in French)

McKinsey A better way to understand internal rate of return

About the author

Article written in June 2021 by Raphaël ROERO DE CORTANZE (ESSEC Business School, Grande Ecole Program – Master in Management, 2019-2022).

How to compute the present value of an asset?

May 15, 2021 by William LONGIN

How to compute the present value of an asset?

In this article, William LONGIN (EDHEC Business School, Global BBA, 2020-2024) elaborates on the concept of Present Value.

What is present value?

The present value (PV) of an asset is usually computed as the value of the stream of its future cash flows discounted at a given rate of return. In the calculation of the present value of an asset, there are two inputs: the expected future cash flows generated by the asset and the discount rate which takes into account the risk on the future cash flows.

The discounting operation takes into account that an amount of money today is worth more than the same amount tomorrow. €100 lent or invested today at an interest rate of 10% is equal to €110 in one year. If you are to receive €100 in one year, you can borrow €90.90 to get this money today. In one year, you will have to repay the amount borrowed €90.90 and the interests €9.10, that is a total cash flow of €100 (that you will pay with the €100 that you are supposed to receive in one year). This refers to the concept of time value of money, best illustrated by the following quote: “Remember that time is money” – Benjamin Franklin (1748).

How is present value computed?

The formula for the present value (PV) of a cash flow occurring at time t, denoted by CF_t, discounted with the discount rate r, is given by:

Present value of a cash flow

The above formula can be used to illustrate the time value of money. What is the present value of €100 obtained in 1 year, 5 years and 10 years? The table below gives the present value by discounting €100 obtained in 1 year, 5 years and 10 years with a discount rate of 10%. Present value shows that money received in the future is not worth as much as an equal amount received today.

This formula can be generalized for a series of cash flows, CF_t, from t=1 to t=T:

Present value of a series of cash flows

Application 1: Computation of the present value of a stock

The concept of present value can be applied to value a stock.

For a stock, the series of cash flows corresponds to the dividends paid by the firm to its stockholders at the end of each period t (DIV_t) and the price P_T at which the stock is supposed to be sold at time T (the horizon of the investor). The present value (PV) is then equal to the discounted value of this series of cash flows at the discount rate r.

Present value of the series of cash flows for a stock

Let us take the example of the valuation of a stock paying a dividend every year. The expected cash flows for dividends is €4 in Year 1, €4 in Year 2, €5 in Year 3, €5 in Year 4, €7 in Year 5 (end of year). The expected resale price in Year 5 is €110 (end of year). Using a discount rate of 10%, the present value of this stock is equal €94.41.

In practice, there are three steps to compute the present value of a stock:

Step 1: Estimate the expected value of future dividends and of the future price
Step 2: Estimate the discount rate given the risk characteristics of the stock
Step 3: Compute the present value

Application 2: Computation of the present value of a bond

The concept of present value can be applied to value a bond. For a fixed-rate bond, the series of cash flows corresponds to the interest paid at the end of each period t (coupon C_t) and the principal value (V) reimbursed at maturity T. The present value (PV) is equal to the discounted value of the series of cash flows at the discount rate r.

Present value of the series of cash flows for a bond

Let us take the example of the valuation of a bond with a nominal value of €1,000, a nominal interest rate of 5%, payment of interests on a yearly basis at the end of the year, and maturing in 5 years. The annual interest is computed as follows: 0.10*1,000 = €100. The last payment corresponds to the interest of the last year (€50) and the reimbursement of the initial capital (€1,000). The series of cash flows is then given by +50, +50, +50, +50, +1,050. Using a discount rate of 5%, the present value of this bond is equal €1,000.

In practice, there are three steps to compute the present value of a bond:

Step 1: Find the characteristics of a bond to compute the cash flows associated to the bond
Step 2: Estimate the discount rate given the risk characteristics of the bond
Step 3: Compute the present value

How to properly compute cash flows?

The future cash flows may be certain or uncertain. When the future cash flows are uncertain, the expected value of the future cash flows, computed as the average of the possible values weighted by their probability, enters the formula for the present value.

Who is using present value?

In financial markets, it is used by traders and investors to estimate the value of financial securities like stocks and bonds.

In the asset management industry, it is also used by asset managers in investment firms (like private equity) to value firms to buy or sell.

In the corporate world, it is used by project managers to estimate the value of the future investments by the firm.

In the accounting context, it is used by accountants to compute the model value of some elements of the balance sheet according to the International Financial Reporting Standards (IFRS).

So, we can see that the concept of present value is useful to a large range of professionals needing to calculate and estimate the value of assets.

▶ William LONGIN My experience as a junior financial analyst at ACE

▶ Maite CARNICERO MARTINEZ How to compute the net present value of an investment in Excel

▶ Jérémy PAULEN How to compute the IRR in Excel

▶ Sébastien PIAT Simple interest rate and compound interest rate

About the author

Article written in May 2021 by William LONGIN (EDHEC Business School, Global BBA, 2020-2024).