How to compute the present value of an asset?
In this article, William LONGIN (EDHEC Business School, Global BBA, 2020-2024) elaborates on the concept of Present Value.
What is present value?
The present value (PV) of an asset is usually computed as the value of the stream of its future cash flows discounted at a given rate of return. In the calculation of the present value of an asset, there are two inputs: the expected future cash flows generated by the asset and the discount rate which takes into account the risk on the future cash flows.
The discounting operation takes into account that an amount of money today is worth more than the same amount tomorrow. €100 lent or invested today at an interest rate of 10% is equal to €110 in one year. If you are to receive €100 in one year, you can borrow €90.90 to get this money today. In one year, you will have to repay the amount borrowed €90.90 and the interests €9.10, that is a total cash flow of €100 (that you will pay with the €100 that you are supposed to receive in one year). This refers to the concept of time value of money, best illustrated by the following quote: “Remember that time is money” – Benjamin Franklin (1748).
How is present value computed?
The formula for the present value (PV) of a cash flow occurring at time t, denoted by CFt, discounted with the discount rate r, is given by:
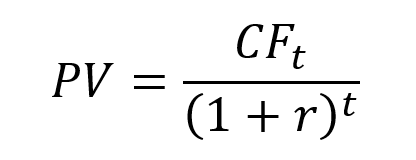
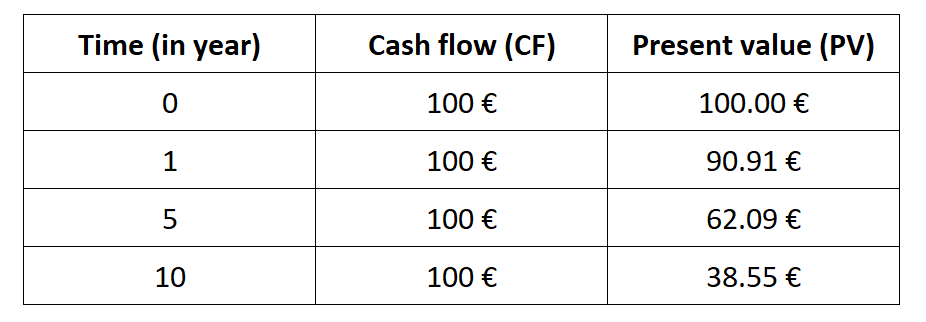
The above formula can be used to illustrate the time value of money. What is the present value of €100 obtained in 1 year, 5 years and 10 years? The table below gives the present value by discounting €100 obtained in 1 year, 5 years and 10 years with a discount rate of 10%. Present value shows that money received in the future is not worth as much as an equal amount received today.
This formula can be generalized for a series of cash flows, CFt, from t=1 to t=T:
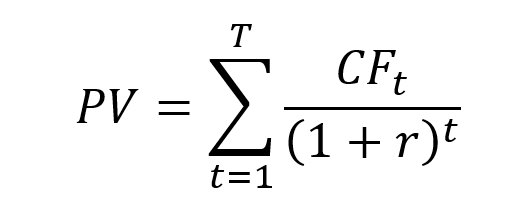
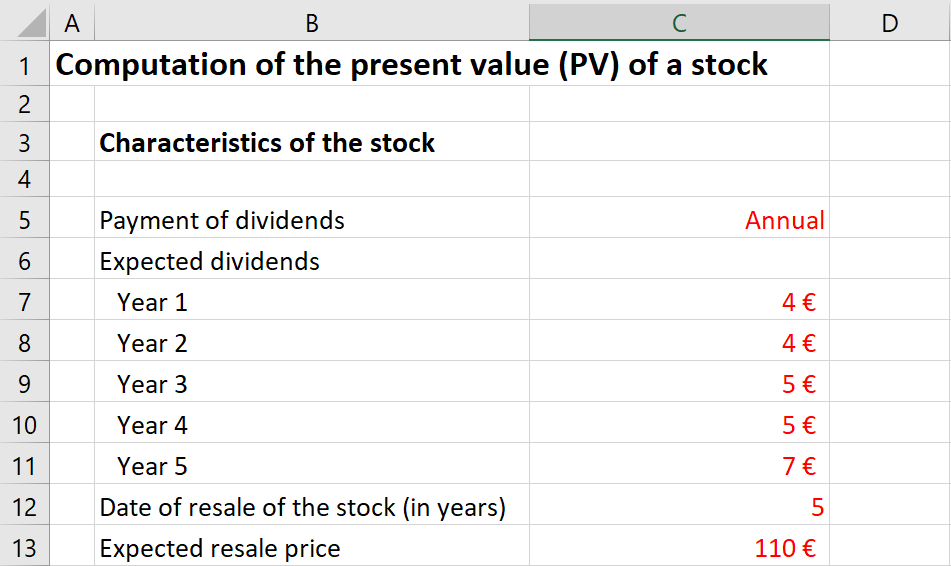
Application 1: Computation of the present value of a stock
The concept of present value can be applied to value a stock.
For a stock, the series of cash flows corresponds to the dividends paid by the firm to its stockholders at the end of each period t (DIVt) and the price PT at which the stock is supposed to be sold at time T (the horizon of the investor). The present value (PV) is then equal to the discounted value of this series of cash flows at the discount rate r.
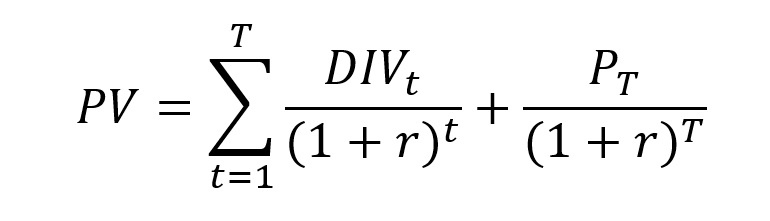
Let us take the example of the valuation of a stock paying a dividend every year. The expected cash flows for dividends is €4 in Year 1, €4 in Year 2, €5 in Year 3, €5 in Year 4, €7 in Year 5 (end of year). The expected resale price in Year 5 is €110 (end of year). Using a discount rate of 10%, the present value of this stock is equal €94.41.
In practice, there are three steps to compute the present value of a stock:
- Step 1: Estimate the expected value of future dividends and of the future price
- Step 2: Estimate the discount rate given the risk characteristics of the stock
- Step 3: Compute the present value
Application 2: Computation of the present value of a bond
The concept of present value can be applied to value a bond. For a fixed-rate bond, the series of cash flows corresponds to the interest paid at the end of each period t (coupon Ct) and the principal value (V) reimbursed at maturity T. The present value (PV) is equal to the discounted value of the series of cash flows at the discount rate r.
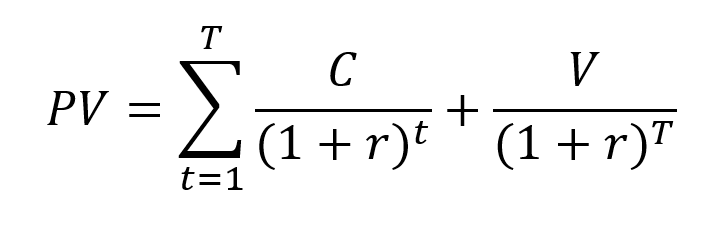
Let us take the example of the valuation of a bond with a nominal value of €1,000, a nominal interest rate of 5%, payment of interests on a yearly basis at the end of the year, and maturing in 5 years. The annual interest is computed as follows: 0.10*1,000 = €100. The last payment corresponds to the interest of the last year (€50) and the reimbursement of the initial capital (€1,000). The series of cash flows is then given by +50, +50, +50, +50, +1,050. Using a discount rate of 5%, the present value of this bond is equal €1,000.
In practice, there are three steps to compute the present value of a bond:
- Step 1: Find the characteristics of a bond to compute the cash flows associated to the bond
- Step 2: Estimate the discount rate given the risk characteristics of the bond
- Step 3: Compute the present value
How to properly compute cash flows?
The future cash flows may be certain or uncertain. When the future cash flows are uncertain, the expected value of the future cash flows, computed as the average of the possible values weighted by their probability, enters the formula for the present value.
Who is using present value?
In financial markets, it is used by traders and investors to estimate the value of financial securities like stocks and bonds.
In the asset management industry, it is also used by asset managers in investment firms (like private equity) to value firms to buy or sell.
In the corporate world, it is used by project managers to estimate the value of the future investments by the firm.
In the accounting context, it is used by accountants to compute the model value of some elements of the balance sheet according to the International Financial Reporting Standards (IFRS).
So, we can see that the concept of present value is useful to a large range of professionals needing to calculate and estimate the value of assets.
Related posts
▶ William LONGIN My experience as a junior financial analyst at ACE
▶ Maite CARNICERO MARTINEZ How to compute the net present value of an investment in Excel
▶ Jérémy PAULEN How to compute the IRR in Excel
▶ Sébastien PIAT Simple interest rate and compound interest rate
About the author
Article written in May 2021 by William LONGIN (EDHEC Business School, Global BBA, 2020-2024).