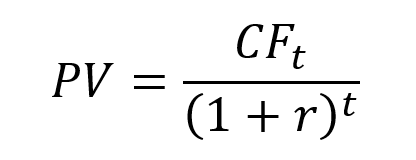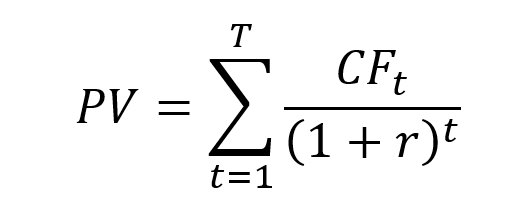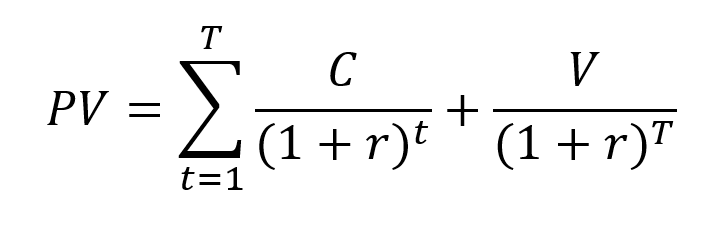How to compute the IRR in Excel

Jeremy PAULEN

In this article, Jérémy PAULEN (ESSEC Business School, Global Bachelor of Business Administration, 2019-2023) explains everything about the IRR function in Excel, which is used to compute the internal rate of return of a series of cash flow to evaluate the financial performance of an investment in relative terms.

What is the IRR?

The IRR represents the internal rate of return of an investment. It is closely related to the net present value (NPV) of the investment as the IRR is the discount rate that makes the NPV equal to zero.

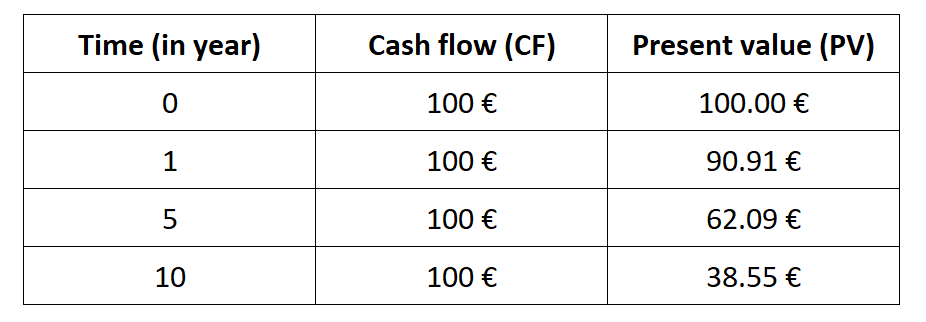
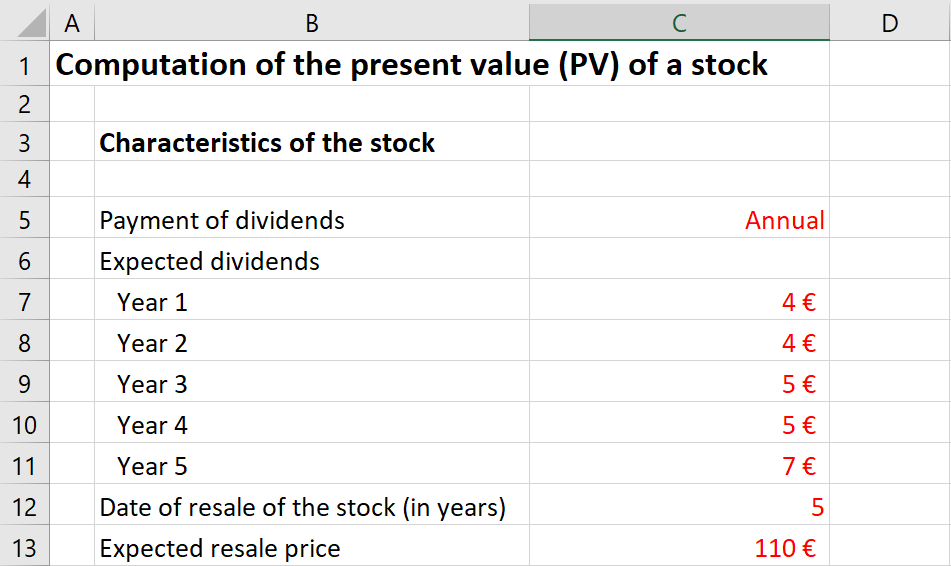
Consider an investment represented by a series of cash flows CF₀, CF₁, CF₂, …, CF_T, which take into account the revenues and expenses of the project computed or forecasted at time 0 leading to capital inflows and outflows for the firm. The NPV of this investment is given by:

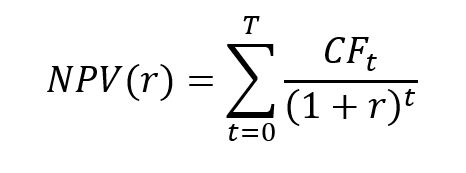
where r is the discount rate that takes into account the risk of the project.

The IRR corresponds to the value of the discount rate for which the NPV is equal to 0:

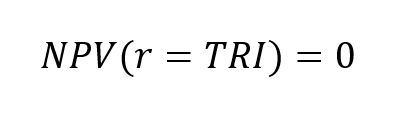
The IRR is the solution of a non-linear equation:

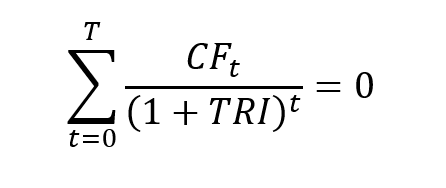
Note that this equation may have one solution, several solutions or no solution according to the sequence of cash flows.

The internal rate of return (IRR) is an important indicator in the decision-making process as it measures the financial performance of a project. The IRR is a relative measure as its unit is a percentage. The NPV is an absolute measure as its unit is the euro, the dollar, etc.

It makes it possible to measure the future financial performance of a project or a company. The higher the IRR is, the more interesting it is to launch the project.

The IRR can therefore be used in the case of a choice to be made between different investment perspectives, but also to evaluate the company’s share buyback programs.

A limit of using the IRR method is that it does not consider the size of a project. Cash flows are simply compared to the amount of capital outlay generating those cash flows. In other words, considering two projects A and B, the IRR of A may be lower than the IRR of B, while the NPV of A may be higher than the NPV of B.

The IRR function in Excel

How to use the IRR function in Excel?

In Excel, you can get the IRR function in the “Formulas” tab.
You can also type “= IRR (value, [guess])” in the cell where you want to compute the IRR.

The IRR function uses the following arguments:

Values: The cash flow series. Cash flows include investment values and net income.
Guess: a number guessed by the user that is close to the expected internal rate of return

Example

Example: consider a new factory modeled by the following series of cash flows:

CF₀ = -$50,000 (initial cost)
CF₁ = +$5,000 (net cash flow in year 1)
CF₂ = +$8,000 (net cash flow in year 2)
CF₃ = +$13,500 (net cash flow in year 3)
CF₄ = +$18,800 (net cash flow in year 4)
CF₅ = +$20,500 (net cash flow in year 5)

Excel file to compute the IRR of a series of cash flows

You can download below a short video which illustrates how to compute the IRR of a series of cash flows with Excel.

Useful resources

Microsoft IRR function

About the author

The article was written in November 2021 by Jérémy PAULEN (ESSEC Business School, Global Bachelor of Business Administration, 2019-2023)

How to compute the present value of an asset?

In this article, William LONGIN (EDHEC Business School, Global BBA, 2020-2024) elaborates on the concept of Present Value.

What is present value?

The present value (PV) of an asset is usually computed as the value of the stream of its future cash flows discounted at a given rate of return. In the calculation of the present value of an asset, there are two inputs: the expected future cash flows generated by the asset and the discount rate which takes into account the risk on the future cash flows.

The discounting operation takes into account that an amount of money today is worth more than the same amount tomorrow. €100 lent or invested today at an interest rate of 10% is equal to €110 in one year. If you are to receive €100 in one year, you can borrow €90.90 to get this money today. In one year, you will have to repay the amount borrowed €90.90 and the interests €9.10, that is a total cash flow of €100 (that you will pay with the €100 that you are supposed to receive in one year). This refers to the concept of time value of money, best illustrated by the following quote: “Remember that time is money” – Benjamin Franklin (1748).

How is present value computed?

The formula for the present value (PV) of a cash flow occurring at time t, denoted by CF_t, discounted with the discount rate r, is given by:

Present value of a cash flow

The above formula can be used to illustrate the time value of money. What is the present value of €100 obtained in 1 year, 5 years and 10 years? The table below gives the present value by discounting €100 obtained in 1 year, 5 years and 10 years with a discount rate of 10%. Present value shows that money received in the future is not worth as much as an equal amount received today.

This formula can be generalized for a series of cash flows, CF_t, from t=1 to t=T:

Present value of a series of cash flows

Application 1: Computation of the present value of a stock

The concept of present value can be applied to value a stock.

For a stock, the series of cash flows corresponds to the dividends paid by the firm to its stockholders at the end of each period t (DIV_t) and the price P_T at which the stock is supposed to be sold at time T (the horizon of the investor). The present value (PV) is then equal to the discounted value of this series of cash flows at the discount rate r.

Present value of the series of cash flows for a stock

Let us take the example of the valuation of a stock paying a dividend every year. The expected cash flows for dividends is €4 in Year 1, €4 in Year 2, €5 in Year 3, €5 in Year 4, €7 in Year 5 (end of year). The expected resale price in Year 5 is €110 (end of year). Using a discount rate of 10%, the present value of this stock is equal €94.41.

In practice, there are three steps to compute the present value of a stock:

Step 1: Estimate the expected value of future dividends and of the future price
Step 2: Estimate the discount rate given the risk characteristics of the stock
Step 3: Compute the present value

Application 2: Computation of the present value of a bond

The concept of present value can be applied to value a bond. For a fixed-rate bond, the series of cash flows corresponds to the interest paid at the end of each period t (coupon C_t) and the principal value (V) reimbursed at maturity T. The present value (PV) is equal to the discounted value of the series of cash flows at the discount rate r.

Present value of the series of cash flows for a bond

Let us take the example of the valuation of a bond with a nominal value of €1,000, a nominal interest rate of 5%, payment of interests on a yearly basis at the end of the year, and maturing in 5 years. The annual interest is computed as follows: 0.10*1,000 = €100. The last payment corresponds to the interest of the last year (€50) and the reimbursement of the initial capital (€1,000). The series of cash flows is then given by +50, +50, +50, +50, +1,050. Using a discount rate of 5%, the present value of this bond is equal €1,000.

In practice, there are three steps to compute the present value of a bond:

Step 1: Find the characteristics of a bond to compute the cash flows associated to the bond
Step 2: Estimate the discount rate given the risk characteristics of the bond
Step 3: Compute the present value

How to properly compute cash flows?

The future cash flows may be certain or uncertain. When the future cash flows are uncertain, the expected value of the future cash flows, computed as the average of the possible values weighted by their probability, enters the formula for the present value.

Who is using present value?

In financial markets, it is used by traders and investors to estimate the value of financial securities like stocks and bonds.

In the asset management industry, it is also used by asset managers in investment firms (like private equity) to value firms to buy or sell.

In the corporate world, it is used by project managers to estimate the value of the future investments by the firm.

In the accounting context, it is used by accountants to compute the model value of some elements of the balance sheet according to the International Financial Reporting Standards (IFRS).

So, we can see that the concept of present value is useful to a large range of professionals needing to calculate and estimate the value of assets.

▶ William LONGIN My experience as a junior financial analyst at ACE

▶ Maite CARNICERO MARTINEZ How to compute the net present value of an investment in Excel

▶ Jérémy PAULEN How to compute the IRR in Excel

▶ Sébastien PIAT Simple interest rate and compound interest rate

About the author

Article written in May 2021 by William LONGIN (EDHEC Business School, Global BBA, 2020-2024).