Capital Structure

Optimal capital structure with corporate and personal taxes: Miller 1977 

by
Snehasish CHINARA

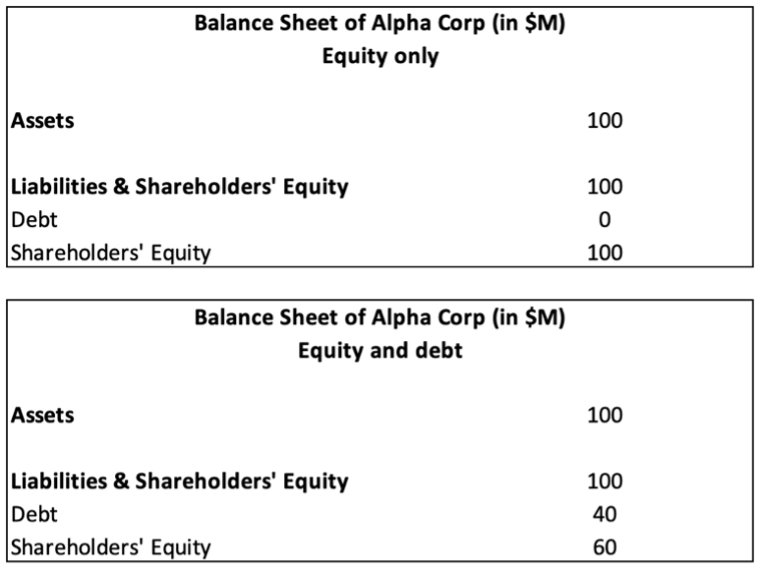
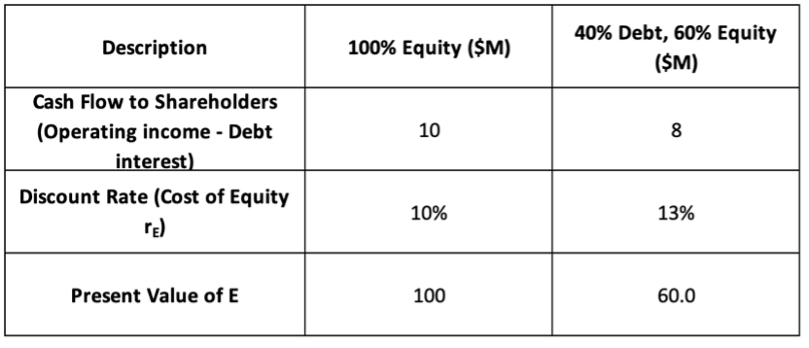
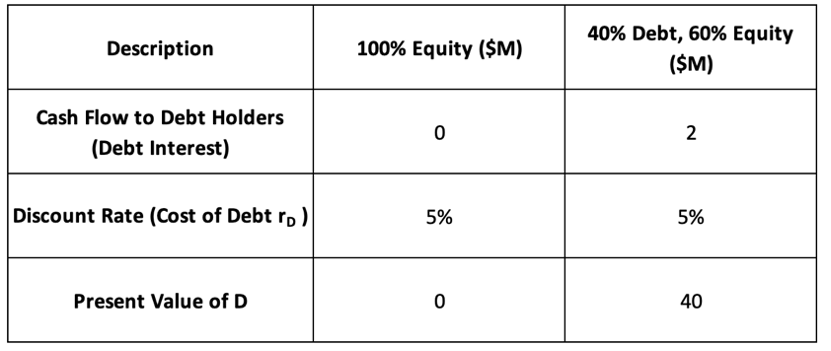
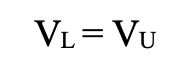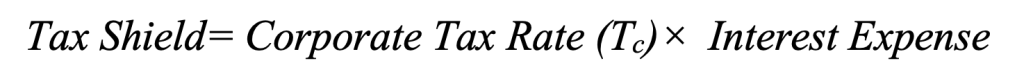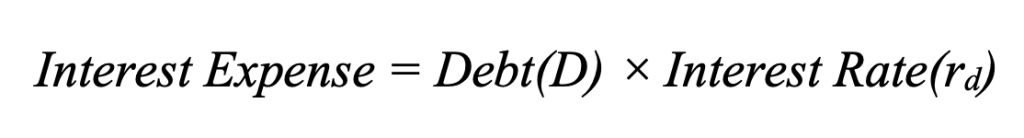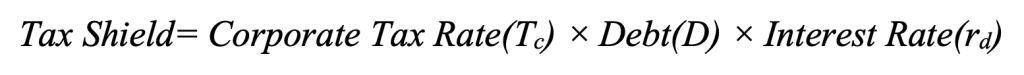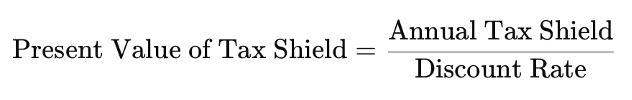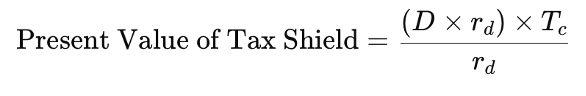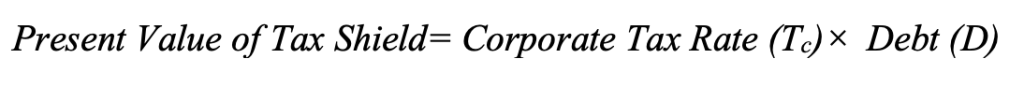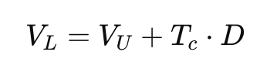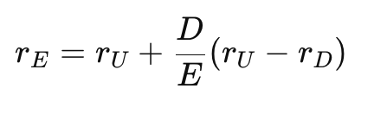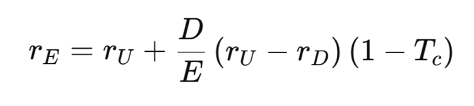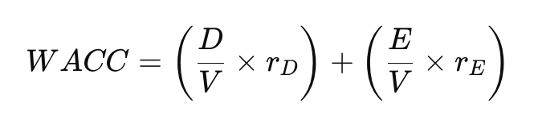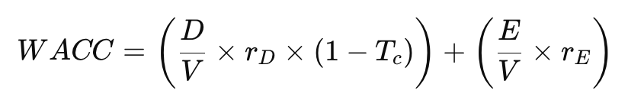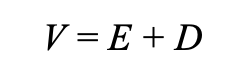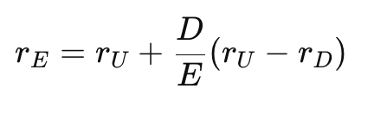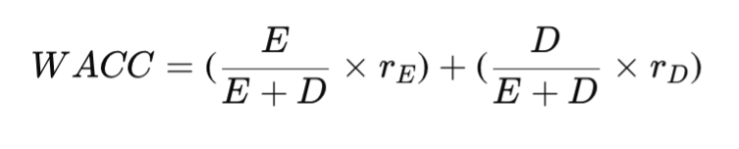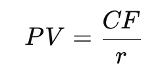In this article, Snehasish CHINARA (ESSEC Business School, Grande Ecole Program – Master in Management, 2022-2025) explores the optimal capital structure for firms, which refers to the balance between debt and equity financing. This post focuses on how the impact of personal taxes on the firm capital structure. The author unpacks Miller’s 1977 proposition, which presents a formula for calculating the right tax advantage of debt, and explains how it helps reconcile theory with what we actually observe in practice.

Introduction

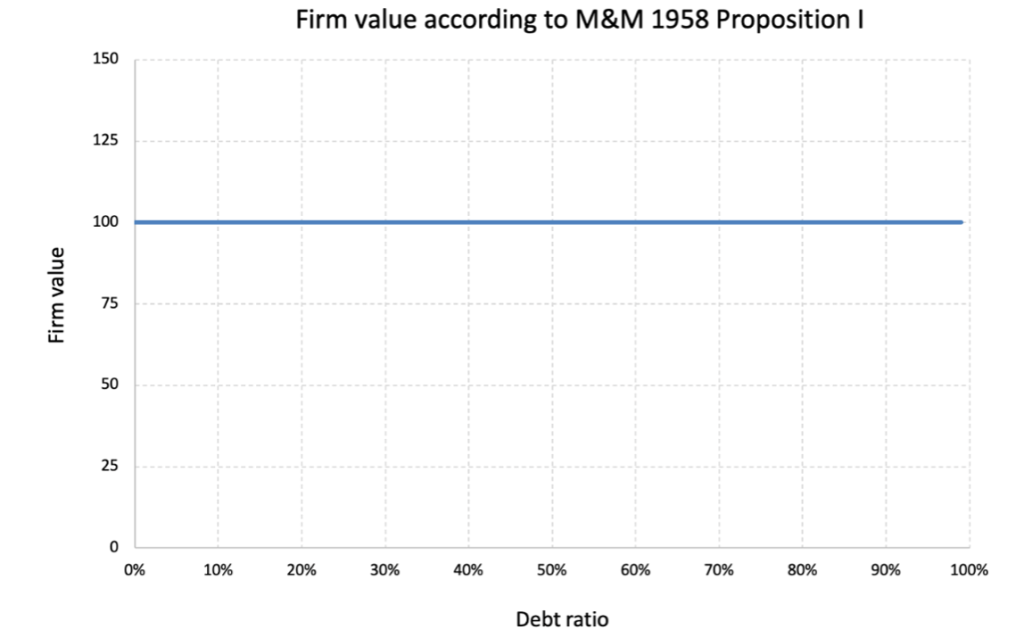
When Modigliani and Miller introduced their capital structure theory in 1958, they shook the foundations of corporate finance. They argued that, in a perfect market with no taxes, no bankruptcy costs, and no frictions, a firm’s value is completely independent of how it is financed. In other words, it doesn’t matter whether a firm uses debt, equity, or a combination of both—the total firm value remains the same.

In 1963, Modigliani and Miller revised their theory to incorporate corporate taxes. With this adjustment, interest payments on debt are tax-deductible, and then provide firms with a “tax shield” that effectively reduces the cost of debt. This made debt financing more attractive than equity, leading to the conclusion that firms should increase their leverage to maximize their value (ideally reaching a 100 debt ratio). In the extreme, this version of the theory suggested that firms should be financed entirely with debt to benefit from the maximum tax advantage.

However, the real world tells a different story. Very few firms rely solely on debt. In fact, most maintain a balanced mix of debt and equity. If debt is supposedly so advantageous under corporate tax rules, why don’t we see more of it being used? This is where Merton Miller’s 1977 work offers a crucial refinement to the theory.

Miller introduced a critical yet often overlooked component into the capital structure discussion: personal taxes. While interest payments are tax-deductible at the corporate level, the income received by investors—whether as interest or dividends—is also subject to personal taxation. Importantly, interest income is often taxed at a higher rate than equity income (like capital gains or dividends). This means the supposed advantage of debt at the corporate level may be offset—or even completely nullified—by the higher tax burden borne by investors.

Modigliani-Miller 1963 Theorem (M&M 1963)

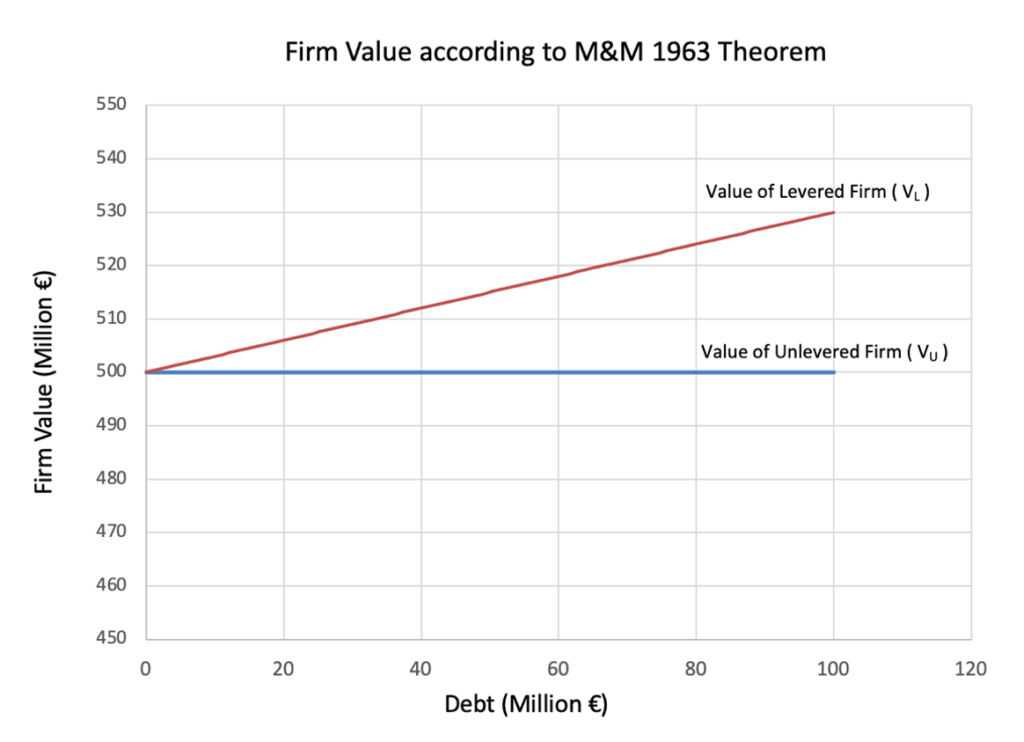
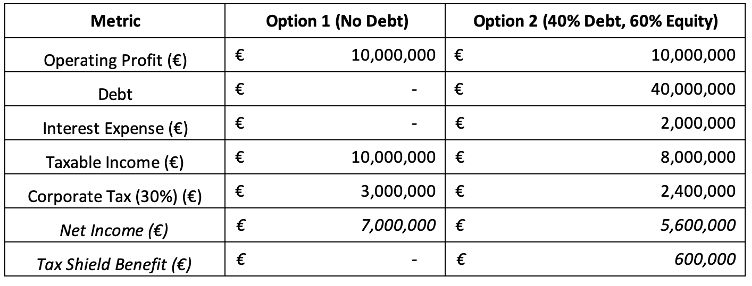
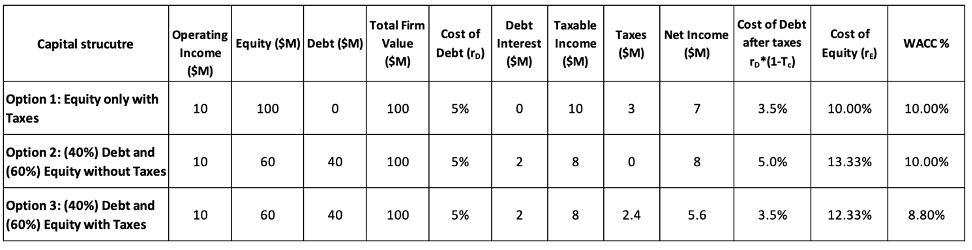
Let us first remind you about the main findings of Modigliani and Miller (1963). In their revision of their first article published a few years earlier (1958), their theory about the firm capital structure introduced corporate taxes, which has a crucial impact on their earlier conclusions which found that the capital structure was irrelevant. They recognized that, in most economies, governments impose corporate income tax, but companies can deduct interest payments on debt from their taxable income. This interest tax-shield increases the after-tax profits of a firm and thereby raises its overall value.

The tax shield refers to the reduction in taxable income that results from interest payments on debt. Since interest expenses are tax-deductible, they effectively reduce the amount of taxes a company owes. This provides a direct financial benefit to firms that use debt financing, making it a valuable tool for optimizing capital structure.

The formula for the tax shield is:

This means that, under the M&M (1963) proposition, the value of a leveraged firm is given by:

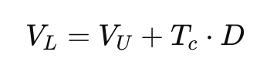
where:

  • VL is the value of a levered firm using debt.

  • VU is the value of a unlevered firm not using debt but only equity

  • Tc is the Corporate tax rate

  • D is the amount of debt of the firm

This formula shows that the value of a firm increases by the amount of tax shield (Tc⋅D) when debt is introduced into the capital structure. The more debt a company takes on, the greater the tax benefit, making debt financing more attractive than equity financing.

Miller (1977): The Role of Personal Taxes in Capital Structure

Modigliani and Miller’s 1963 revision made a powerful case for debt: because interest payments are tax-deductible, firms enjoy a tax shield that reduces their cost of capital. The logical (but extreme) implication of this idea was that firms should maximize debt in their capital structure. However, the theory still fell short of explaining reality—most firms do not load up on debt. Why?

This is where Merton Miller’s 1977 paper brought a major refinement. While M&M (1963) focused on corporate taxes, Miller highlighted the crucial role of personal taxes paid by investors. Specifically, he noted that:

  • Interest income (from bonds or loans) is typically taxed at a higher personal rate (TPi),

  • While equity income (via dividends or capital gains) is often taxed at a lower rate (TPe).

Thus, although the firm saves taxes through debt, the investor receiving interest income may lose part of that advantage due to higher personal taxes. Miller argued that the tax benefit of debt is not universal—it depends on the relative tax positions of the firm and its investors.

Miller quantified the net tax advantage of debt with the following formula:

where:

  • TPi is the personal tax rate on interest income

  • TPe is the personal tax rate on equity income (dividends/capital gains)

  • Tc is the corporate tax rate

This expression compares the after-tax returns from debt and equity financing, from both the firm’s and investor’s perspectives.

Value of a Levered Firm according to Miller (1977)

In Miller (1977), the value of the firm incorporates both:

1. The corporate tax shield (from M&M 1963), and

2. The personal tax disadvantage from investor taxation on interest income.

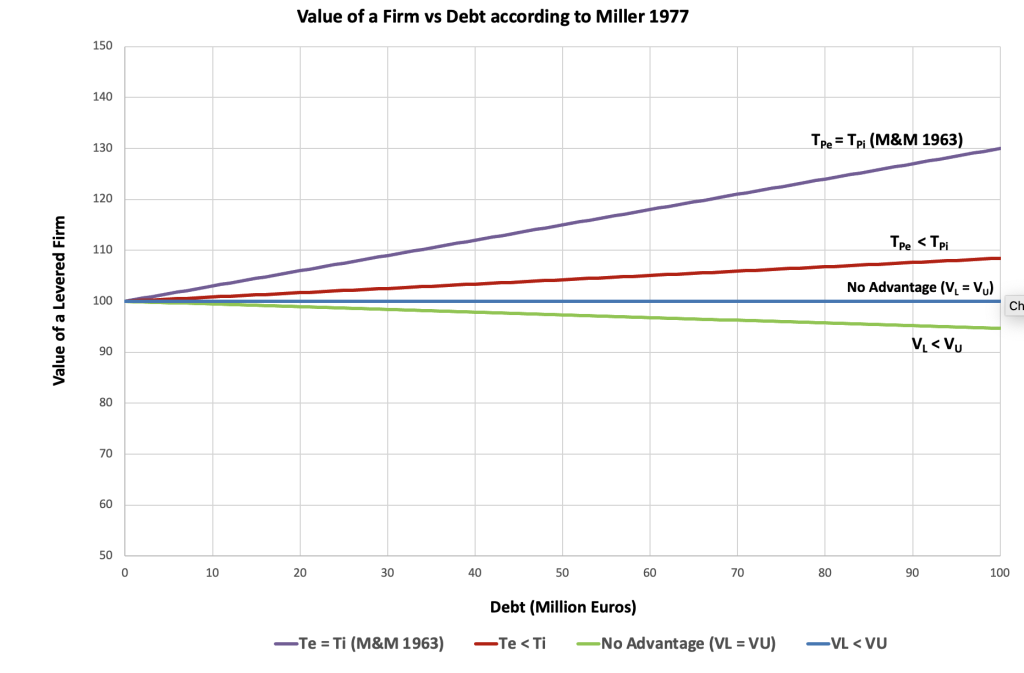
Unlike M&M 1963 (which assumed value keeps increasing with leverage due to tax shields), Miller showed that the firm’s value plateaus at an equilibrium level, reflecting the offsetting effect of personal taxes.

There isn’t a single formula as elegant as in M&M 1963 because Miller focuses on market equilibrium, not firm-level maximization. But we can express the adjusted value of a levered firm relative to the unlevered firm as:

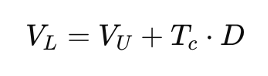
that is,

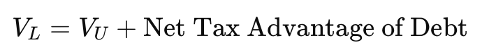
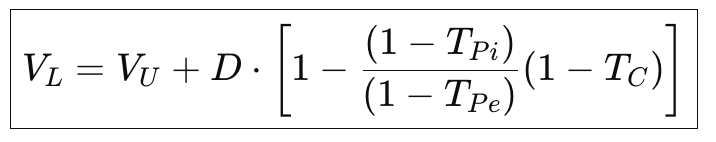
where:

  • VL is the value of a levered firm using debt.

  • VU is the value of a unlevered firm not using debt but only equity

  • Tc is the Corporate tax rate

  • TPi is the personal tax rate on interest income

  • TPe is the personal tax rate on equity income (dividends/capital gains)

  • D is the amount of debt of the firm

Figure 1. Firm Value vs Debt according to Miller 1977 Theorem

where:

  • Tc is the Corporate tax rate

  • TPi is the personal tax rate on interest income

  • TPe is the personal tax rate on equity income (dividends/capital gains)

The Equilibrium Capital Structure Across Firms

One of the most insightful—and often misunderstood—contributions of Miller (1977) is that there is no single “optimal” capital structure for all firms. Instead of recommending that every company should maximize debt (as M&M 1963 might suggest), Miller argued that the optimal mix of debt and equity depends on the broader market, not just individual firm decisions. His approach introduced a market-level equilibrium perspective, which helps us understand the diverse financing strategies we observe in the real world.

Miller recognized that not all investors are taxed equally. Some investors—like pension funds, endowments, or individuals in low tax brackets—are less affected by taxes on interest income. These investors prefer debt because they can earn stable interest income without facing significant tax penalties. On the other hand, investors in higher tax brackets might favour equity, particularly because capital gains and dividends are often taxed at lower rates than interest income.

This diversity in investor preferences (from different personal tax rates) creates a kind of natural balance in the financial markets. Some firms will issue more debt to attract income-focused investors, while others will rely more on equity to appeal to investors who value capital gains. Over time, this leads to a market equilibrium in which different firms adopt different capital structures based on the preferences of the investors they attract.

In reality, we do not see all firms aggressively using debt to lower their tax bills. Instead, we see some firms—like utilities or financial institutions—using higher levels of debt, while others—like tech startups or growth firms—rely more on equity. This variation observed in practice aligns perfectly with Miller’s theory. The aggregate tax advantage of debt is “used up” across the economy, so not every firm needs to (or should) leverage itself heavily.

Firms essentially compete for investor types, and their capital structure decisions reflect the marginal investor’s personal tax situation. In this way, the equilibrium is not found at the level of a single firm, but across the entire set of firms.

How Miller (1977) Redefined the Cost of Equity and WACC from Modigliani-Miller (1963)

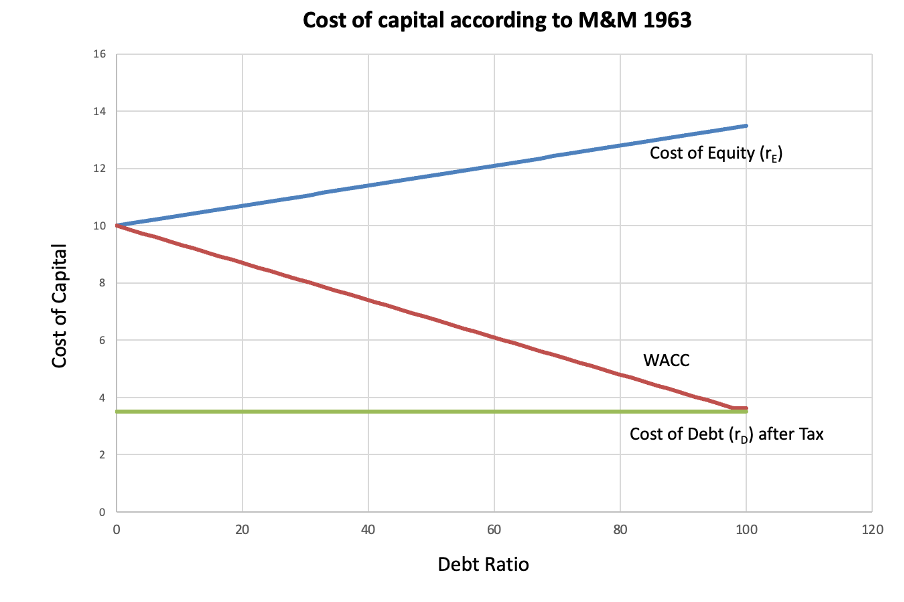
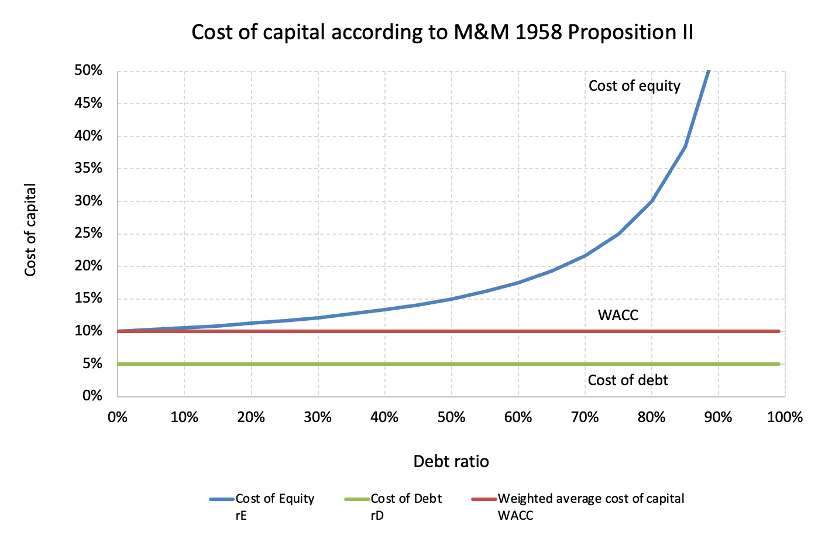
In M&M (1963), the introduction of corporate taxes led to a crucial insight: because interest payments are tax-deductible, debt financing creates a tax shield that reduces the firm’s Weighted Average Cost of Capital (WACC). The model predicted that, as leverage increases, WACC decreases, and firm value rises—implying that a firm should use as much debt as possible to minimize its cost of capital.

This had a direct impact on the cost of equity as well. In M&M (1963), the cost of equity (rE) increases with leverage to compensate for the rising risk faced by shareholders:

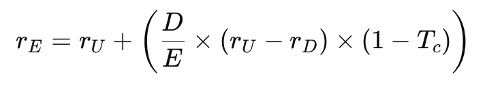
where:

  • rE is the cost of equity for a levered firm

  • rU is the cost of equity for an unlevered firm

  • rD is the cost of debt

  • D/E is the debt to equity ratio measuring leverage

Here, while the cost of equity increases due to higher financial risk, the overall WACC falls, thanks to the tax shield:

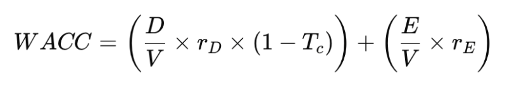
Where: V is the Value of the firm (V= D + E)

Miller (1977) introduced personal taxes into the equation—something that M&M (1963) completely ignored. He observed that investors are not only taxed at the corporate level but also at the personal level:

  • Interest income is taxed at the personal level (personal tax rate on interest income: TPi)

  • Equity dividends and capital gains are taxed at the personal level (personal tax rate on equity: TPe)

Crucially, interest income is taxed more heavily than equity dividends and capital gains: TPi > TPe. This is the case in the United States and most developed countries.

This alters the perceived tax advantage of debt as the benefit of corporate tax deductibility may be neutralized—or even outweighed—by the higher taxes on interest income.

While Miller (1977) didn’t give a neatly adjusted cost of equity formula like Modigliani and Miller (1963), he did show that the tax advantage of debt financing is not universal—it depends on both corporate and personal tax rates. This led to a redefinition of the net tax advantage of debt, which in turn affects WACC:

And so, the adjusted value of the tax shield, and by extension the impact of debt on WACC, becomes:

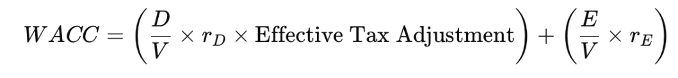
Using this expression, the WACC becomes:

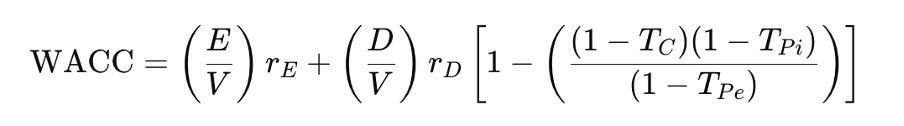
where,

  • Tc is the Corporate tax rate

  • TPi is the personal tax rate on interest income

  • TPe is the personal tax rate on equity income (dividends/capital gains)

  • D/V is the proportion of debt in the capital structure

  • E/V is the Proportion of equity in the capital structure

  • rE is the cost of equity for a levered firm

  • rD is the cost of debt

This means that the WACC no longer declines indefinitely with debt. Instead, as the tax burden on interest income increases (via Ti ), the marginal benefit of debt diminishes. At market equilibrium, the advantage of debt disappears, and WACC flattens—explaining why we observe moderate, not extreme, debt usage in practice.

  • If Ti > Te and corporate tax Tc is high, debt still offers a net tax advantage, though smaller than in M&M (1963).

  • If the term in brackets equals zero, there is no net tax advantage—WACC remains flat regardless of leverage.

  • If the term becomes negative, equity becomes more tax-efficient, and adding debt raises the WACC.

Why Should I Be Interested in This Post?

In corporate finance, the debate around how much debt a firm should take on is far from settled. While traditional models like Modigliani-Miller (1963) emphasize the tax benefits of debt, they ignore the taxes investors pay. This post introduces the groundbreaking Miller (1977) framework, which shows how personal taxes can offset corporate tax advantages, reshaping our understanding of optimal capital structure. If you’re a finance student, investor, or aspiring professional, understanding this equilibrium-based view will give you a more realistic—and nuanced—perspective on how real-world firms decide between debt and equity.

Related posts on the SimTrade blog

   ▶ Snehasish CHINARA Optimal capital structure with taxes: Modigliani and Miller 1963

   ▶ Snehasish CHINARA Optimal capital structure with no taxes: Modigliani and Miller 1958

   ▶ Snehasish CHINARA Solvency and Insolvency in the Corporate World

   ▶ Snehasish CHINARA Illiquidity, Liquidity and Illiquidity in the Corporate World

   ▶ Snehasish CHINARA Illiquidity, Solvency & Insolvency : A Link to Bankruptcy Procedures

   ▶ Snehasish CHINARA Chapter 7 vs Chapter 11 Bankruptcies: Insights on the Distinction between Liquidations & Reorganisations

   ▶ Snehasish CHINARA Chapter 7 Bankruptcies: A Strategic Insight on Liquidations

   ▶ Snehasish CHINARA Chapter 11 Bankruptcies: A Strategic Insight on Reorganisations

   ▶ Akshit GUPTA The bankruptcy of Lehman Brothers (2008)

   ▶ Akshit GUPTA The bankruptcy of the Barings Bank (1996)

   ▶ Anant JAIN Understanding Debt Ratio & Its Impact On Company Valuation

Useful resources

US Courts Data – Bankruptcy

S&P Global – Bankruptcy Stats

Statista – Bankruptcy data

About the author

The article was written in July 2025 by Snehasish CHINARA (ESSEC Business School, Grande Ecole Program – Master in Management, 2022-2025).

Optimal capital structure with taxes: Modigliani and Miller 1963

by
Snehasish CHINARA

In this article, Snehasish CHINARA (ESSEC Business School, Grande Ecole Program – Master in Management, 2022-2025) explores the optimal capital structure for firms, which refers to the balance between debt and equity financing. This post dives into the article written by Modigliani and Miller (1963) which explores the case of corporate tax and a frictionless market (no bankruptcy costs).

Introduction to Modigliani and Miller Propositions

In 1958, Franco Modigliani and Merton Miller introduced a groundbreaking theory on capital structure, famously known as the M&M Proposition. Their research concluded that, under certain ideal conditions, the way a company finances itself—whether through debt or equity—does not affect its overall value. This result, known as the Capital Structure Irrelevance Principle, was based on assumptions such as no corporate taxes, no bankruptcy costs, and perfect capital markets. The intuition behind this idea is simple: if investors can create their own leverage by borrowing personally at the same rate as firms, then a company’s financing mix should not matter for its value.

According to M&M Proposition I (1958), in a frictionless world:

where:

  • VL is the value of a levered firm using debt.

  • VU is the value of a unlevered firm not using debt but only equity

Key Assumptions:

  • No taxes (in reality, firms pay corporate taxes).

  • No bankruptcy costs (in reality, firms pay costs if they go bankrupt).

  • No financial distress (in reality, too much debt can make investors nervous).

However, this initial model had a major limitation: it ignored the effect of corporate taxes. In reality, most governments tax corporate profits, but they allow firms to deduct interest expenses on debt from taxable income. This means that using debt provides a tax advantage, which was missing from the 1958 model. Recognizing this, Modigliani and Miller revised their original work in 1963, introducing the impact of corporate taxes. Their new findings dramatically changed the conclusion: debt financing increases firm value because interest payments reduce taxable income, creating a tax shield. This update laid the foundation for modern corporate finance by showing that, with corporate taxes, firms should prefer debt over equity.

Modigliani-Miller 1963 Theorem (M&M 1963)

Modigliani and Miller’s 1963 revision to their capital structure theory introduced the concept of corporate taxes, which has a crucial impact on their earlier conclusions. They recognized that, in most economies, governments impose corporate income tax, but companies can deduct interest payments on debt from their taxable income. This interest tax-shield increases the after-tax profits of a firm and thereby raises its overall value.

The tax shield refers to the reduction in taxable income that results from interest payments on debt. Since interest expenses are tax-deductible, they effectively reduce the amount of taxes a company owes. This provides a direct financial benefit to firms that use debt financing, making it a valuable tool for optimizing capital structure.

The formula for the tax shield is:

Since interest expense is calculated as:

Therefore, the tax shield for a single year becomes:

The Modigliani-Miller (1963) model assumes perpetual debt primarily for simplification and mathematical clarity. The use of perpetual debt helps in calculating the present value of the tax shield without the need for complex discounting over a finite period.

If the firm has perpetual debt, meaning it never repays the principal and continues paying interest forever, the total value of the tax shield is found by calculating the present value of all future tax shield benefits. Since the tax shield is received every year indefinitely, its present value is:

Using the cost of debt (rd) as the discount rate, we get:

The (rd) cancels out, simplifying to:

This means that, under the M&M (1963) proposition, the value of a leveraged firm is given by:

where:

  • VL is the value of a levered firm using debt.

  • VU is the value of a unlevered firm not using debt but only equity

  • Tc is the Corporate tax rate

  • D is the amount of debt of the firm

This formula shows that the value of a firm increases by the amount of tax shield (Tc⋅D) when debt is introduced into the capital structure. The more debt a company takes on, the greater the tax benefit, making debt financing more attractive than equity financing.

Figure 1. Firm Value vs Debt according to M&M 1963 Theorem

In simple terms, taxes make debt financing more beneficial because firms pay interest on debt before paying taxes, reducing their taxable income. On the other hand, dividends paid to equity shareholders are not tax-deductible, meaning that firms must pay taxes on their entire profit before distributing dividends.

Implication for Capital Structure Decisions:

Firms benefit from using debt due to the tax shield, leading to a preference for more leverage.

The Modigliani-Miller (1963) model with taxes suggests that because of the tax shield on debt, a firm’s value increases as it takes on more debt. The formula for value of a levered firm according to M&M(1963) shows that every additional unit of debt directly increases firm value by the tax savings it provides. In theory, this means that a firm should finance itself entirely with debt (100% debt financing) to maximize its value. This is a significant departure from M&M (1958), where capital structure had no effect on firm value.

Limitations

However, in real-world scenarios, firms do not rely solely on debt. This is because excessive debt increases the risk of financial distress and bankruptcy costs, which M&M (1963) did not initially consider.

Case Study: Implications of M&M 1963 (Optimal Capital Structure with corporate taxes)

Alpha Corp operates in an imperfect capital market (with taxes only). It has two financing options for the capital structure:

  • Option 1: equity only (100% equity, 0% debt)

  • Option 2: debt and equity (60% equity, 40% debt)

Each option funds a $100 million investment that generates an annual operating income of $10 million. The risk-free interest rate is 5%, and the corporate tax rate is 30%.

Figure 2. Simplified Balance Sheet of Alpha Corp

Table 1. M&M 1963: an Example

Based on Table 1, the key takeaways are as follows:

1.Debt Creates a Tax Shield:

  • Under Option 2 (40% debt, 60% equity), Alpha Corp pays €2 million in interest expense, reducing taxable income from €10 million to €8 million.

  • This results in a lower corporate tax payment (€2.4 million instead of €3 million), leading to a €600,000 tax shield benefit.

2.Net Income is Lower with Debt, But Firm Value Increases:

  • Despite reducing tax liability, net income under Option 2 (€5.6 million) is lower than Option 1 (€7 million) because of interest expenses.

  • However, the firm’s total value increases due to the tax shield, meaning equity holders still benefit from debt financing.

How Modigliani-Miller (1963) Redefined the Cost of Equity and WACC from Modigliani-Miller (1958)

In Modigliani-Miller (1958), the firm’s capital structure—the mix of debt and equity—was considered irrelevant to its overall cost of capital (WACC) and, by extension, its firm value. This proposition, based on ideal market conditions (no taxes, no bankruptcy costs), argued that whether a firm is financed by debt or equity, the overall cost of capital remains unchanged. The cost of equity increases with leverage because equity holders demand higher returns to compensate for the additional financial risk, but this increase in cost of equity was offset by the lower cost of debt. Therefore, WACC stayed constant regardless of a firm’s capital structure.

However, when Modigliani and Miller (1963) introduced corporate taxes into their model, they demonstrated a significant change in the cost of capital (WACC) and cost of equity dynamics. With the tax deductibility of interest payments on debt, the cost of debt is effectively reduced, which leads to a reduction in WACC. This creates a clear benefit for firms that use more debt in their capital structure, making debt financing a value-enhancing tool. Let’s explore these key differences in detail.

Impact on the Cost of Equity (rE)

MM (1958) – Cost of Equity Increases with Leverage

Under the Modigliani-Miller (1958) framework, the cost of equity (rE) increases as a firm takes on more debt because equity holders demand higher returns for taking on additional risk due to leverage. The relationship between cost of equity and leverage is described by the following formula:

where:

  • rE is the cost of equity for a levered firm

  • rU is the cost of equity for an unlevered firm

  • rD is the cost of debt

  • D/E is the debt to equity ratio measuring leverage

This formula shows that as a firm increases its debt, its cost of equity increases to compensate for the increased financial risk borne by equity holders. However, since debt is cheaper than equity, the overall WACC remains unchanged.

MM (1963) – Tax Shield Reduces the Impact on Cost of Equity In MM (1963), the introduction of corporate taxes changes the scenario. Since interest expenses on debt are tax-deductible, the effective cost of debt (rD) becomes lower. This reduces the overall risk for the firm and, therefore, the increase in the cost of equity (rE) is less severe than in MM (1958). The new formula for cost of equity becomes:
where Tc is the corporate tax rate. The (1 – Tc) term reduces the increase in cost of equity (rE), because the firm’s debt is now partially subsidized by the tax shield. This shows that while leverage still increases the cost of equity (rE), the effect is less pronounced in the presence of tax deductibility of interest payments.

Impact on the Weighted Average Cost of Capital (WACC)

M&M (1958) – WACC Remains Constant Regardless of Leverage

In MM (1958), because the increase in the cost of equity (rE) offsets the benefit of cheaper cost of debt (rD), the WACC remains constant no matter the debt-to-equity ratio. The formula for WACC in this model is:

where:

  • V=D+E is the total firm value

  • rE is the cost of equity for a levered firm

  • rD is the cost of debt

  • D is the total debt

  • E is the total equity

According to MM (1958), since debt and equity are in perfect balance (i.e., the increase in the cost of equity (rE) is offset by the lower cost of debt (rD)), the WACC stays constant. The capital structure—how much debt or equity a firm uses—has no effect on the overall cost of capital or the firm’s value in a world without taxes.

MM (1963) – WACC Declines as Debt Increases

With the introduction of taxes, MM (1963) shows that WACC decreases as a firm increases its debt. The tax shield created by the deductibility of interest payments lowers the effective cost of debt (rD), making debt financing more attractive.

The formula for after-tax WACC in MM (1963) is:

In this scenario, debt financing becomes more advantageous because the firm can lower its overall WACC by utilizing debt, which reduces the tax burden. The WACC decreases as a firm increases its leverage (debt) because the cost of debt (rD) is reduced due to the tax shield, and the cost of equity (rE) increases at a slower rate due to the reduced impact of debt on financial risk.

Figure 3. Modigliani-Miller View Of Gearing And WACC: With Taxation (MM 1963)

Case Study: Implications of M&M 1963 (Optimal Capital Structure with corporate taxes)

Alpha Corp operates in a capital market (no bankruptcy costs, and no market imperfections). It has two financing options:

  • Option 1: Fully equity-financed (No debt with Corporate Taxes of 30%)

  • Option 2: 40% Debt, 60% Equity (without Corporate Taxes)

  • Option 3: 40% Debt, 60% Equity (with Corporate Taxes of 30% )

Each option funds a $100 million investment that generates an annual operating income of $10 million. The risk-free interest rate is 5%, and the required return on equity is 10%.

Figure 4. Modigliani-Miller View Of Gearing And WACC: With Taxation (MM 1963)

Table 2. M&M 1963: an Example

Key takeaways from this example are as follows :

1. Corporate Taxes Make Debt Financing More Attractive by Reducing the Effective Cost of Debt

  • In a no-tax world (M&M 1958, Option 2), firms are indifferent between debt and equity, as capital structure does not affect WACC.

  • However, M&M (1963) proves that in a taxed environment (Option 3), debt financing creates value because interest payments reduce taxable income, leading to lower corporate taxes.

  • This is called the “tax shield” effect, where firms pay less in taxes by using debt, increasing after-tax cash flows available to shareholders.

2. WACC Declines with Leverage When Corporate Taxes Exist, Unlike in M&M (1958)

  • In M&M (1958) (no taxes, Option 2), WACC remains constant at 10%, regardless of leverage.

  • M&M (1963) (Option 3) introduces taxes, causing WACC to drop to 8.80% due to the tax shield.

  • Strategic Takeaway: Firms can reduce their cost of capital and increase firm value by incorporating moderate levels of debt into their capital structure.

3. Cost of Equity Increases with Debt, But the Tax Shield Reduces the Rate of Increase

  • Higher leverage increases financial risk for shareholders, leading to a higher required return on equity (rE).

  • In Option 2 (M&M 1958, No Taxes), introducing 40% debt raises the cost of equity to 13.33% due to added risk.

  • In Option 3 (M&M 1963, With Taxes), the cost of equity only increases to 12.33%, because the tax shield offsets part of the financial risk.

4. After-Tax Cost of Debt is Lower than the Cost of Equity, Making Debt a Cheaper Financing Option

  • The cost of debt before taxes is 5%.

  • Due to the corporate tax rate (30%), the effective cost of debt is reduced: rDafter-tax= rD ×(1−Tc)

  • Comparing Financing Costs in Option 3:

    • Cost of Equity (rE) = 12.33%

    • After-Tax Cost of Debt (rD) = 3.5%

  • Debt financing is significantly cheaper than equity financing after adjusting for the tax shield.

  • Firms should utilize debt strategically to lower overall financing costs.

5. The Trade-Off Between Tax Benefits and Financial Distress Risk Determines the Optimal Capital Structure

  • M&M (1963) suggests using more debt to reduce WACC, but in reality, excessive debt increases financial distress risks.

  • While debt reduces WACC through the tax shield, too much debt leads to higher bankruptcy risks, credit downgrades, and operational constraints.

  • Most firms balance debt and equity to optimize WACC, using debt to take advantage of tax savings without excessive financial risk.

Takeaways on Optimal Debt Structure and Bankruptcy Costs from M&M 1963 Theorem

The Modigliani-Miller (1963) proposition demonstrated that the presence of corporate taxes fundamentally changes the implications of capital structure on firm value. Unlike their earlier 1958 proposition, where capital structure was deemed irrelevant, the 1963 revision highlighted the benefits of debt financing due to the tax shield effect. Since interest expenses on debt are tax-deductible, firms can reduce their taxable income and, consequently, their tax obligations. This finding suggests that, in a world with corporate taxes and no other frictions, firms should finance themselves entirely with debt to maximize their value.

The M&M (1963) proposition remains a cornerstone in understanding capital structure decisions, demonstrating that debt financing enhances firm value through tax savings. However, in practice, firms must carefully balance leverage to avoid excessive financial distress. The optimal capital structure is not purely debt-driven but rather a carefully calibrated mix of debt and equity that maximizes firm value while maintaining financial stability.

Why Should I Be Interested in This Post?

This post explains a key concept in corporate finance—how debt financing affects firm value through corporate tax benefits and financial risks. If you’re a student, finance professional, or investor, understanding the Modigliani-Miller (1963) proposition will help you grasp why companies use debt. With clear explanations, real-world examples, and Excel-based analysis, this post provides practical insights into optimal capital structure decisions.

Related posts on the SimTrade blog

   ▶ Snehasish CHINARA Optimal capital structure with no taxes: Modigliani and Miller 1958

   ▶ Snehasish CHINARA Solvency and Insolvency in the Corporate World

   ▶ Snehasish CHINARA Illiquidity, Liquidity and Illiquidity in the Corporate World

   ▶ Snehasish CHINARA Illiquidity, Solvency & Insolvency : A Link to Bankruptcy Procedures

   ▶ Snehasish CHINARA Chapter 7 vs Chapter 11 Bankruptcies: Insights on the Distinction between Liquidations & Reorganisations

   ▶ Snehasish CHINARA Chapter 7 Bankruptcies: A Strategic Insight on Liquidations

   ▶ Snehasish CHINARA Chapter 11 Bankruptcies: A Strategic Insight on Reorganisations

   ▶ Akshit GUPTA The bankruptcy of Lehman Brothers (2008)

   ▶ Akshit GUPTA The bankruptcy of the Barings Bank (1996)

   ▶ Anant JAIN Understanding Debt Ratio & Its Impact On Company Valuation

Useful resources

US Courts Data – Bankruptcy

S&P Global – Bankruptcy Stats

Statista – Bankruptcy data

About the author

The article was written in January 2025 by Snehasish CHINARA (ESSEC Business School, Grande Ecole Program – Master in Management, 2022-2025).

Optimal capital structure with no taxes: Modigliani and Miller 1958

by
Snehasish CHINARA

In this article, Snehasish CHINARA (ESSEC Business School, Grande Ecole Program – Master in Management, 2022-2025) explores the optimal capital structure for firms, which refers to the balance between debt and equity financing. This post dives into the article written by Modigliani and Miller (1958) which explores the case of no corporate tax and a frictionless market (no bankruptcy costs).

Introduction to Capital Structure

Capital structure refers to the mix of debt and equity financing that a company uses to fund its operations and growth. It is a critical component of corporate finance, as it directly impacts a firm’s cost of capital, financial risk, and overall valuation. The choice of capital structure affects a company’s ability to raise funds, weather economic downturns, and pursue strategic investments.

Capital structure is reflected in a company’s balance sheet, which provides a snapshot of its financial position at a given point in time. Specifically, it is composed of two primary financing sources:

  • Debt (Liabilities) – Found under the Liabilities section, debt includes short-term borrowings, long-term loans, bonds payable, and lease obligations. Debt financing requires periodic interest payments and repayment of principal, increasing financial obligations but also benefiting from potential tax shields.

  • Equity (Shareholders’ Equity) – Located under the Shareholders’ Equity section, equity includes common stock, preferred stock, retained earnings, and additional paid-in capital. Equity financing does not require fixed interest payments but dilutes ownership among shareholders.

Table 1 below gives a simplified version of a balance sheet.

Table 1 – Simplified Balance Sheet Example

Table 1 shows that the firm finances its $350M in assets with $140M in debt (40%) and $210M in equity (60%), demonstrating a debt-to-equity ratio of 0.67 (=140/210). Additionally, the debt ratio, D/(D+E), measures the proportion of total financing that comes from debt 40% (=140/(140+210)). This indicates that a significant portion of capital is funded through borrowed money, allowing the company to take advantage of the use of debt, but also exposing it to higher financial risk if it faces difficulties in meeting debt obligations. These ratios are a few key indicators used to assess a company’s financial leverage and risk exposure.

A higher reliance on debt can lead to increased financial risk due to interest obligations, while too much equity financing may dilute shareholder returns. Therefore, finding an optimal capital structure is crucial for maintaining a healthy balance between risk, return, and financial stability.

Capital structure is one of the most fundamental decisions in corporate finance, influencing a firm’s financial stability, cost of capital, and overall value. At the heart of this discussion lies the Modigliani-Miller (M&M) theorems (M&M 1958 and M&M 1963), which provides the foundational framework for understanding how a company’s choice between debt and equity affects its valuation. However, while MM’s initial work (1958) proposed that capital structure is irrelevant in a frictionless market, real-world complexities such as taxation, bankruptcy costs, and financial distress challenge this assumption, leading to more nuanced theories.

The Modigliani-Miller 1958 Theorem (M&M 1958)

The Modigliani-Miller theorem (M&M 1958), introduced in 1958 by Franco Modigliani and Merton Miller, is a cornerstone of modern corporate finance. It provides a theoretical framework for understanding the role of capital structure in determining a firm’s value. M&M 1958’s core argument is that in a perfect market, a firm’s value is independent of its capital structure, meaning that the choice between debt and equity financing has no impact on firm valuation.

M&M 1958 Proposition I: Capital Structure Irrelevance

For the problem of the determination of the optimal capital structure of the firm, we assume that the firm (and its managers) seek to maximize the financial or economic value of the shareholders’ equity.

M&M’s first proposition states that, in a world with no taxes, no transaction costs, and perfect information, the total value of a firm (V) is unaffected by its financing decisions. Whether a company is financed with 100% equity, 100% debt (almost), or any combination of both, its market value remains the same because investors can create their own leverage through homemade financing.

M&M’s first proposition says that a company’s value is determined by its business operations (profits, assets, and growth potential), not by how it finances those operations. Since in a perfect world, investors can create leverage on their own. If a company doesn’t use debt, an investor can borrow money separately to create the same effect. This means that whether the company uses debt or not, its overall value remains the same.

For a firm with market value V, total assets A, and financed by debt D and equity E:

According to M&M Proposition I, in a frictionless world:

where:

  • VL is the value of a levered firm using debt.

  • VU is the value of a unlevered firm not using debt but only equity

Key Assumptions:

  • No taxes (in reality, firms pay corporate taxes).

  • No bankruptcy costs (in reality, firms pay costs if they go bankrupt).

  • No financial distress (in reality, too much debt can make investors nervous).

Figure 1. Firm Value vs Debt Ratio according to M&M 1958: Proposition I

In Figure 1, according to M&M 1958 Proposition I, the firm value remains constant regardless of the debt ratio. The flat blue line represents the idea that whether a firm is 100% equity-financed or takes on debt, its total value does not change in a perfect world with no taxes, no bankruptcy costs, and no market imperfections.

M&M 1958 Proposition II: Cost of Equity and Leverage Relation

While M&M Proposition I states that firm value is independent of capital structure, Proposition II explains how leverage affects the cost of equity (and then then total cost of financing measured by the weighted average cost of capital or WACC). It shows that as a firm increases its debt, equity becomes riskier, leading to an increase in the cost of equity (rE) to compensate for higher financial risk.

When a firm increases its leverage, its cost of debt (rD) is typically lower than its cost of equity (rE) due to the priority of debt holders in the capital structure and the fixed nature of interest payments. However, as leverage rises, the firm’s equity becomes riskier because debt obligations take precedence, amplifying the volatility of residual earnings available to shareholders. According to Modigliani-Miller Proposition II, this higher financial risk leads to an increase in the required return on equity (rE), as shareholders demand greater compensation for bearing the amplified risk exposure.

where:

  • rE = cost of equity for a levered firm

  • rU = cost of equity for an unlevered firm

  • rD = cost of debt

  • D/E = debt to equity ratio measuring leverage

This formula highlights that with higher leverage, the cost of equity increases, offsetting any benefit from the lower cost of debt. Thus, while leverage amplifies returns, it also raises financial risk, maintaining the firm’s overall cost of capital.

Shareholders bear more risk as leverage increases due to the following reasons –

  • Residual Claimants: Shareholders are last in line for cash flows, meaning higher debt increases fixed interest obligations, reducing the certainty of equity returns.

  • Earnings Volatility: With more debt, small fluctuations in operating profits cause larger swings in equity returns, making equity riskier.

  • Default & Financial Distress Risk: If debt levels rise too much, the firm faces a higher probability of default or financial distress, further increasing required equity returns.

WACC according to M&M 1958 Proposition II

The Weighted Average Cost of Capital (WACC) is a key financial metric that represents a firm’s overall cost of financing by combining the costs of equity and debt. Under Modigliani-Miller Proposition II (1958), the WACC is given by the formula:

Where:

  • WACC = Weighted Average Cost of Capital

  • E = Value of equity

  • D = Value of debt

  • rE = Cost of equity (which increases with leverage)

  • rD = Cost of debt (fixed by assumption)

M&M 1958 Proposition II states that as a firm increases its debt financing, its cost of equity rE rises to compensate for the additional financial risk. However, because debt is cheaper than equity, the lower cost of debt rD balances out the increase in rE, keeping WACC constant.

Figure 2. Modigliani-Miller View Of Gearing And WACC: No Taxation (MM 1958 Proposition II)

Based on Figure 2, implication for firms are as follows:

  • In a world with no taxes and bankruptcy costs, leverage does not create or destroy firm value.

  • Higher leverage increases equity risk, leading to higher required returns for shareholders.

  • The Weighted Average Cost of Capital (WACC) remains constant regardless of debt-equity mix.

If a company borrows money (takes on debt), it must pay interest no matter how well the business performs. If profits drop, shareholders get whatever is left after paying the debt, which makes equity riskier. Because of this extra risk, shareholders demand a higher return, which increases the cost of equity.

Case Study: Implications of M&M 1958 (Optimal Capital Structure with no taxes)

Alpha Corp operates in a perfect capital market (no taxes, no bankruptcy costs, and no market imperfections). It has two financing options:

  • Option 1: Fully equity-financed (No debt)

  • Option 2: 40% Debt, 60% Equity

Each option funds a $100 million investment that generates an annual operating income of $10 million. The risk-free interest rate is 5%, and the required return on equity is 10%.

Figure 3. Simplified Balance Sheet of Alpha Corp

Table 2. M&M 1958: an Example

Based on Table 2, the key takeaways are as follows:

1. Firm Value Remains Constant

  • In both financing scenarios (100% Equity vs. 40% Debt, 60% Equity), the total value of the firm remains $100M.

  • This aligns with Modigliani-Miller Proposition I (1958), which states that in a perfect capital market, capital structure does not impact firm value.

2. Cost of Equity Increases with Leverage

  • In the 100% equity scenario, the required return on equity (rE) is 10%.

  • When the firm takes on 40% debt, the cost of equity (rE) increases to 13%, reflecting the additional financial risk borne by equity holders.

  • This aligns with Modigliani-Miller Proposition II (1958), which states that as leverage increases, equity holders require a higher return due to increased financial risk.

3. WACC Remains Constant

  • Despite the change in capital structure, the Weighted Average Cost of Capital (WACC) remains at 10%.

  • This reinforces M&M Proposition II, which states that in a perfect market, using debt does not lower the firm’s overall cost of capital.

4. Impact on Cash Flows & Present Values

  • Equity holders receive lower cash flows ($8M) under 40% debt financing due to interest payments ($2M) to debt holders.

  • However, the present value of debt ($40M) + present value of equity ($60M) = $100M, meaning that the firm’s total value remains unchanged regardless of financing choices.

Computation of Cash Flows and the DCF Approach

Table 3. Cash Flow for shareholders using cost of equity

Table 4. Cash Flow for debt holders using cost of debt

The Discounted Cash Flow (DCF) approach is used to determine the value of equity (E) and debt (D) by discounting their respective cash flows.

1. Cash Flows to Shareholders (Equity Holders)

  • Formula: CF to Equity= Operating Income −Interest Payments

  • Computation:

    • 100% Equity Case:10M−0=10M

    • 40% Debt, 60% Equity Case:10M−2M=8M

2. Cash Flows to Debt Holders

  • Formula: CF to Debt= Interest Payment = Debt × rD

  • Computation: 40% Debt, 60% Equity Case: 40M×5%=2M

3. Present Value (PV) of Equity and Debt Using DCF