Distributions statistiques : variable discrète vs variable continue
Dans cet article, Shengyu ZHENG (ESSEC Business School, Grande Ecole – Master in Management, 2020-2024) explique les distributions statistiques pour des variables aléatoires discrètes et continues.
Variables aléatoires discrète et continue
Une variable aléatoire est une variable dont la valeur est déterminée d’après la réalisation d’un événement aléatoire. Plus précisément, la variable (X) est une fonction mesurable depuis un ensemble de résultats (Ω) à un espace mesurable (E).
X : Ω → E
On distingue principalement deux types de variables aléatoires : discrètes et continues.
Une variable aléatoire discrète prend des valeurs dans un ensemble dénombrable comme l’ensemble des entiers naturels. Par exemple, le nombre de points marqués lors d’un match de basket est une variable aléatoire discrète, car elle ne peut prendre que des valeurs entières telles que 0, 1, 2, 3, etc. Les probabilités associées à chaque valeur possible de la variable aléatoire discrète sont appelées probabilités de masse.
En revanche, une variable aléatoire continue prend des valeurs dans un ensemble non dénombrable comme l’ensemble des nombres réels. Par exemple, la taille ou le poids d’une personne sont des variables aléatoires continues, car elles peuvent prendre n’importe quelle valeur réelle positive. Les probabilités associées à une variable aléatoire continue sont déterminées par une fonction de densité de probabilité. Cette fonction permet de mesurer la probabilité que la variable aléatoire se situe dans un intervalle donné de valeurs.
Méthodes pour décrire des distributions statistiques
Afin de mieux comprendre une variable aléatoire, il y a plusieurs moyens pour décrire la distribution de la variable.
Calcul des statistiques
Une statistique est le résultat d’une suite d’opérations appliquées à un ensemble d’observations appelé échantillon et une mesure numérique qui résume une caractéristique de cet ensemble. Par exemple, la moyenne est un exemple de statistiques.
Les statistiques peuvent être divisées en deux types principaux : les statistiques descriptives et les statistiques inférentielles.
Les statistiques descriptives sont utilisées pour résumer et décrire les caractéristiques de base d’un ensemble de données. Elles comprennent des mesures telles que les moments d’une distribution (la moyenne, la variance, le skewness, le kurtosis, …). Une explication plus détaillée est disponible dans l’article Moments de la distribution.
Les statistiques inférentielles, quant à elles, sont utilisées pour faire des inférences sur une population à partir d’un échantillon de données. Elles incluent des tests d’hypothèses, des intervalles de confiance, des analyses de régression, des modèles prédictifs, etc.
Histogramme
Un histogramme est un type de graphique qui permet de représenter la distribution des données d’un échantillon. Il est constitué d’une série de rectangles verticaux, où chaque rectangle représente une plage de valeurs de la variable étudiée (appelée classe), et dont la hauteur correspond à la fréquence des observations de cette classe.
L’histogramme est un outil très utilisé pour visualiser la distribution des données et pour identifier les tendances et les formes dans les données pour les variables discrètes ainsi que continues discrétisées.
Fonction de masse et fonction de densité
Une fonction de masse de probabilité est une fonction mathématique qui permet de décrire la distribution de probabilité d’une variable aléatoire discrète.
La fonction de masse de probabilité associe à chaque valeur possible de la variable aléatoire discrète une probabilité. Par exemple, si X est une variable aléatoire discrète prenant les valeurs 1, 2, 3 et 4 avec des probabilités respectives de 0,2, 0,3, 0,4 et 0,1, alors la fonction de masse de probabilité de X (loi multinomiale) est donnée par :
P(X=1) = 0,2
P(X=2) = 0,3
P(X=3) = 0,4
P(X=4) = 0,1
Il est important de noter que la somme des probabilités pour toutes les valeurs possibles de la variable aléatoire doit être égale à 1, c’est-à-dire, pour toute variable aléatoire discrète X :
∑ P(X=x) = 1
Figure 1. Fonction de masse d’une loi multinomiale (pour une variable discrète).
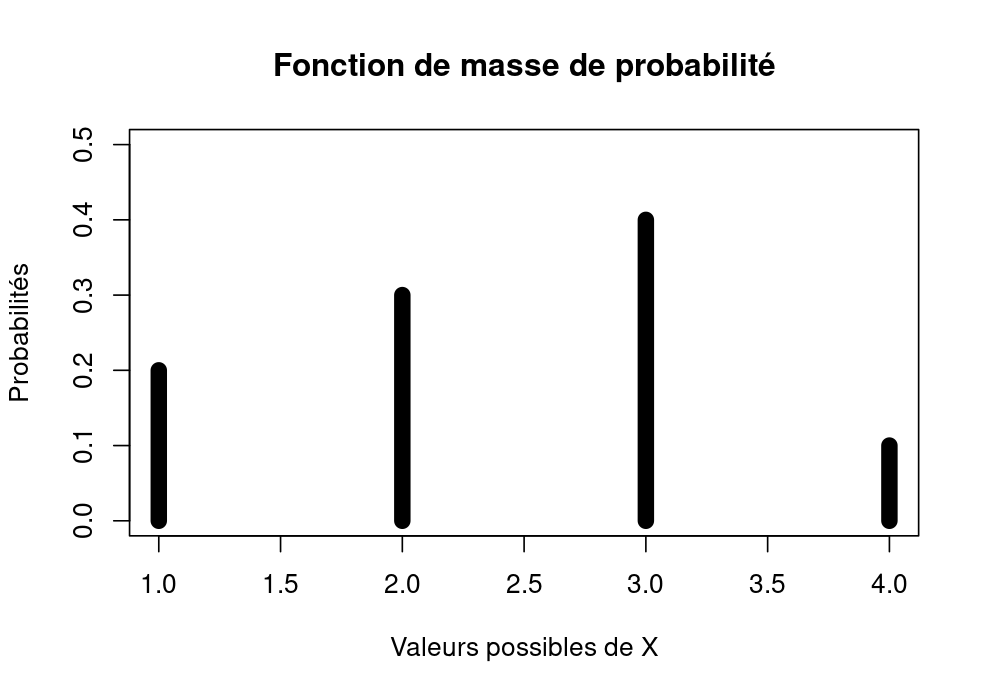
Source : calcul par l’auteur
Par contre, une fonction de densité représente la distribution de probabilité d’une variable aléatoire continue. La fonction de densité permet de calculer la probabilité que la variable aléatoire prenne une valeur dans un intervalle donné.
Graphiquement, l’aire sous la courbe de la fonction de densité entre deux valeurs a et b correspond à la probabilité que la variable aléatoire prenne une valeur dans l’intervalle [a, b].
Il est important de noter que la fonction de densité est une fonction continue, positive et intégrable sur tout son domaine. L’intégrale de la fonction de densité sur l’ensemble des valeurs possibles de la variable aléatoire est égale à 1.
Figure 2. Fonction de densité d’une loi normale (pour une variable continue).
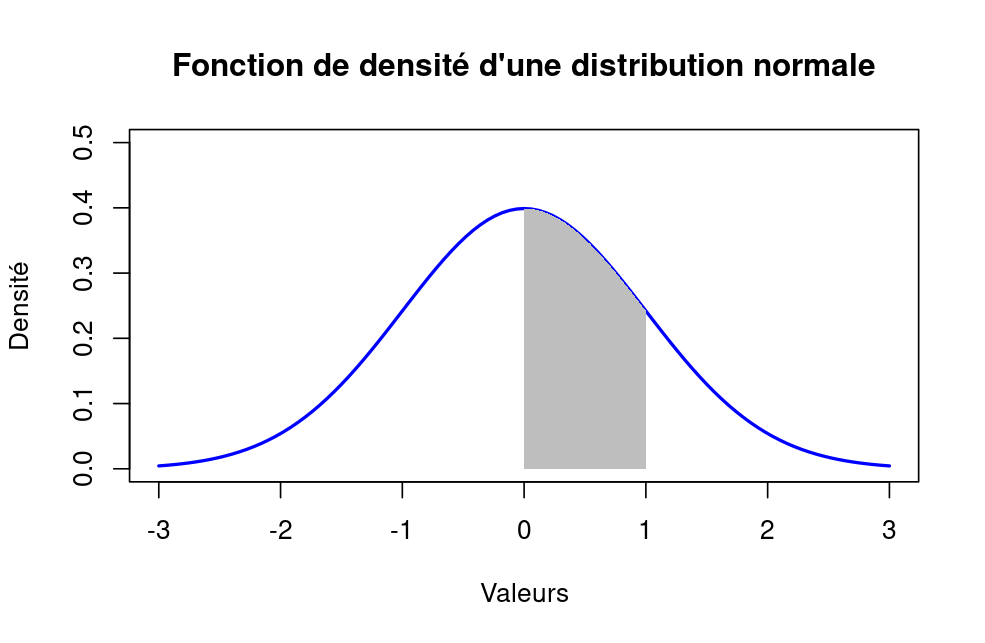
Source : calcul par l’auteur
Fonction de répartition
La fonction de répartition (ou fonction de distribution cumulative) est une fonction mathématique qui décrit la probabilité qu’une variable aléatoire prenne une valeur inférieure ou égale à une certaine valeur donnée. Elle est définie pour toutes les variables aléatoires, qu’elles soient continues ou discrètes.
Pour une variable aléatoire discrète, la fonction de répartition F(x) est définie comme la somme des probabilités des valeurs inférieures ou égales à x :
F(x) = P(X ≤ x) = Σ P(X = xi) pour xi ≤ x
Pour une variable aléatoire continue, la fonction de répartition F(x) est définie comme l’intégrale de la densité de probabilité f(x) de -∞ à x :
F(x)=P(X≤x)= ∫-∞xf(t)dt
Exemples
Dans cette partie, nous allons prendre deux exemples d’analyse de distribution statistique, l’un d’une variable aléatoire discrète et l’autre d’une variable continue.
Variable discrète : résultat du lancer d’un dé à six faces
Le jeu de lancer de dé à six faces consiste à lancer un dé pour obtenir un résultat aléatoire entre 1 et 6, correspondant aux six faces du dé. Les résultats ne prennent que les valeurs entières (1, 2, 3, 4, 5 et 6) et ils ont tous une probabilité identique de 1/6.
Dans cet exemple, le code R permet de simuler N lancers de dé et de visualiser la distribution des N résultats à l’aide d’un histogramme. En utilisant ce code, il est possible de simuler des parties de lancer de dé et d’analyser les résultats pour mieux comprendre la distribution des probabilités.
Si cette expérience aléatoire est répétée 1 000 fois, nous arrivons à un résultat dont l’histogramme est comme :
Figure 3. Histogramme des résultats de lancers d’un dé à six faces.
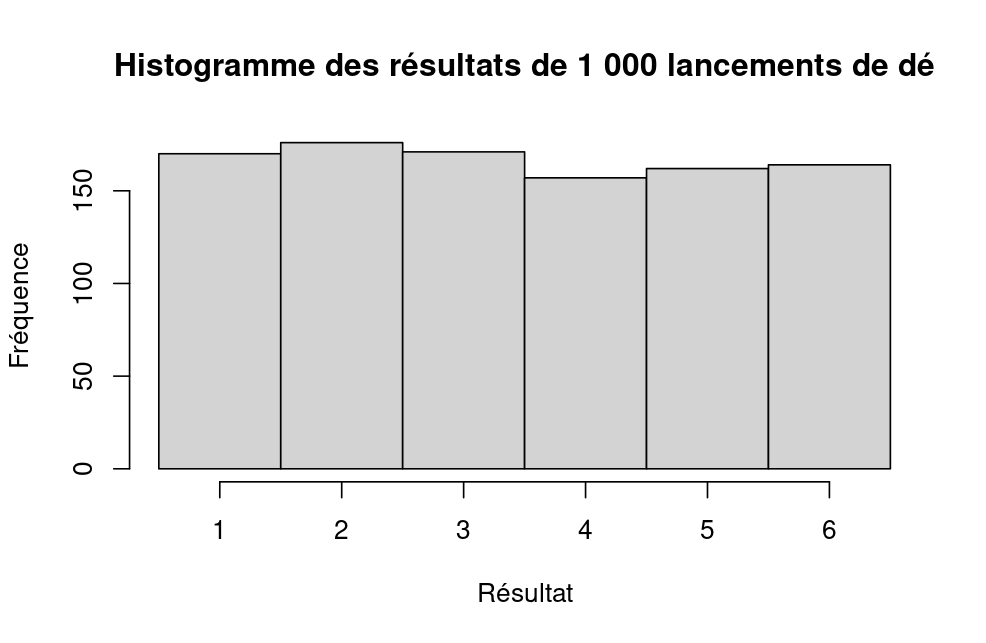
Source : calcul par l’auteur
Nous constatons que les résultats sont distribués d’une manière équilibrée et ont la tendance de converger vers la probabilité théorique 1/6.
Variable continue : rendments de l’indice CAC40
Le rendement d’un indice d’actions comme le CAC 40 pour le marché français est une variable aléatoire continue parce qu’elle peut prendre toutes les valeurs réelles.
Nous utilisons un historique de l’indice boursier journalier pour des cours de clôture de l’indice CAC 40 du 1er avril 2021 au 1er avril 2023 pour calculer des rendements journalières (rendements logarithmiques).
En finance, la distribution des rendements journalières de l’indice CAC 40 est souvent modélisée par une loi normale, même si la loi normale ne modélise pas forcément bien la distribution observée, surtout les queues de distributions observées. Dans le graphique ci-dessous, nous voyons que la distribution normale ne décrit pas bien la distribution réelle.
Figure 4. Fonction de densité des rendements journalières de l’indice CAC 40 (variable continue).
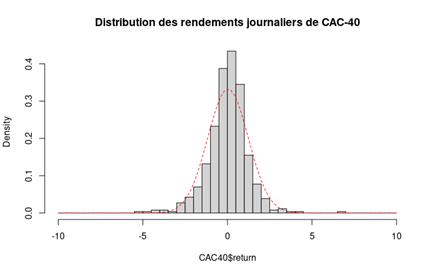
Source : calcul par l’auteur
Pour des observations issues pour une variable continue, il est toujours possible de regrouper les observations dans des intervalles et de représenter dans un histogramme.
La table 1 ci-dessous donne les statistiques descriptives pour les rendements journalières de l’indice CAC 40.
Table 1. Statistiques descriptives pour les rendements journalières de l’indice CAC 40.
| Statistiques descriptives | Valeur |
| Moyenne | 0.035 |
| Médiane | 0.116 |
| Écart-type | 1.200 |
| Skewness | -0.137 |
| Kurtosis | 6.557 |
Les résultats du calcul des statistiques descriptives correspondent bien à ce que nous pouvons remarquer du graphique. La distribution des rendements a une moyenne légèrement positive. La queue de la distribution empirique est plus épaisse que celle de la distribution normale vu les survenances des rendements (positives ou négatives) extrêmes.
Fichier R pour cet article
A propos de l’auteur
Cet article a été écrit en octobre 2023 par Shengyu ZHENG (ESSEC Business School, Grande Ecole Program – Master in Management, 2020-2024).


