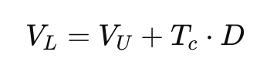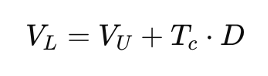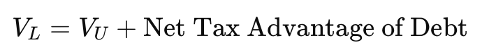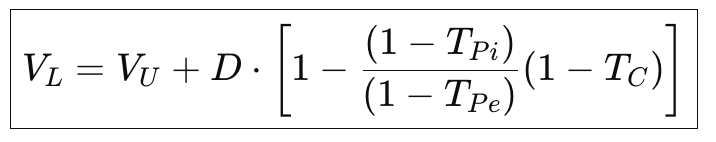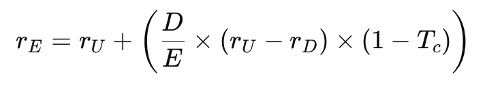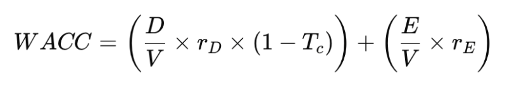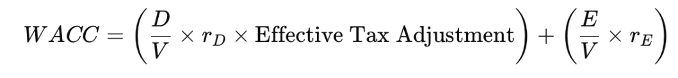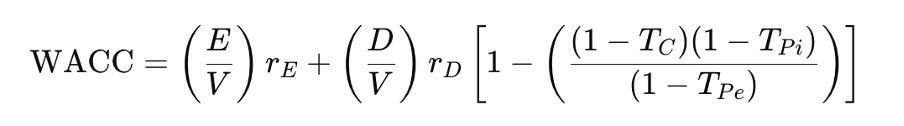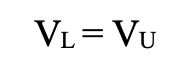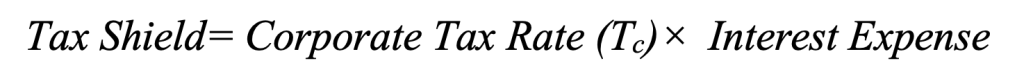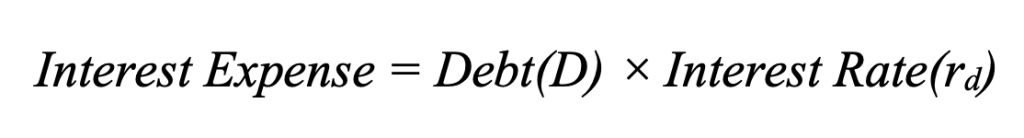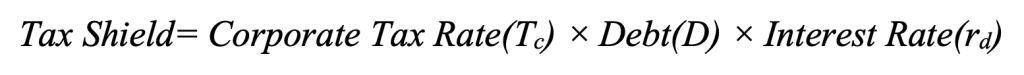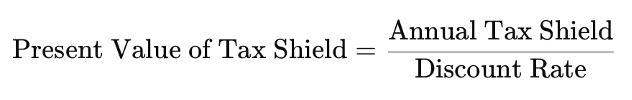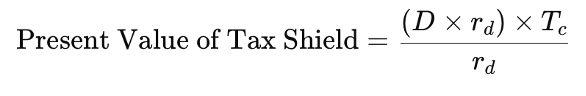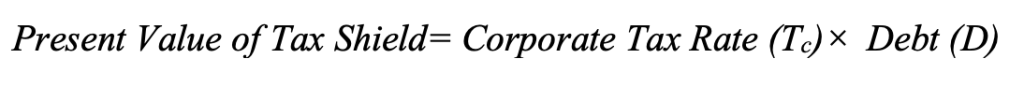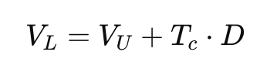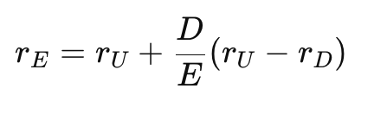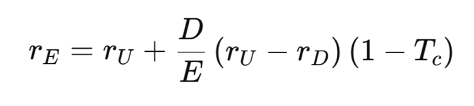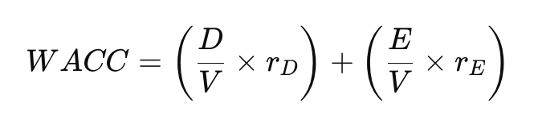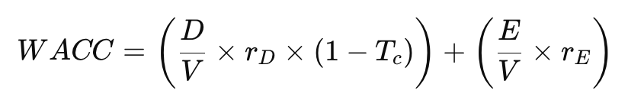optimal capital structure

Academic perspectives on optimal debt structure and bankruptcy costs

by
Snehasish CHINARA

In this article, Snehasish CHINARA (ESSEC Business School, Grande Ecole Program – Master in Management, 2022-2025) explores the academic evolution of capital structure theory, focusing on the delicate balance between debt and equity financing. Starting from the foundational Modigliani and Miller propositions, this post delves into how the introduction of real-world frictions—particularly bankruptcy costs and financial distress—gave rise to the Trade-Off Theory.

Introduction to Capital Structure

Capital structure refers to the mix of debt and equity financing that a company uses to fund its operations and growth. It is a critical component of corporate finance, as it directly impacts a firm’s cost of capital, financial risk, and overall valuation.

Capital structure is reflected in a company’s balance sheet, which provides a snapshot of its financial position at a given point in time. Specifically, it is composed of two primary financing sources:

1. Debt (Liabilities) – Found under the Liabilities section, debt includes short-term borrowings, long-term loans, bonds payable, and lease obligations. Debt financing requires periodic interest payments and repayment of principal, increasing financial obligations but also benefiting from potential tax shields.

2.Equity (Shareholders’ Equity) – Located under the Shareholders’ Equity section, equity includes common stock, preferred stock, retained earnings, and additional paid-in capital. Equity financing does not require fixed interest payments but dilutes ownership among shareholders.

Table 1 below gives a simplified version of a balance sheet.

Table 1 – Simplified Balance Sheet Example

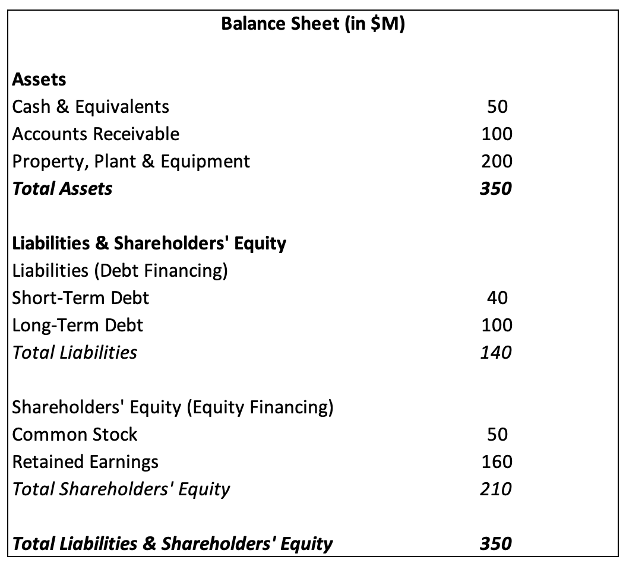
Table 1 shows that the firm finances its $350M in assets with $140M in debt (40%) and $210M in equity (60%), demonstrating a debt-to-equity ratio of 0.67 (=140/210). Additionally, the debt ratio, D/(D+E), measures the proportion of total financing that comes from debt 40% (=140/(140+210)). This indicates that a significant portion of capital is funded through borrowed money, allowing the company to take advantage of the use of debt, but also exposing it to higher financial risk if it faces difficulties in meeting debt obligations. These ratios are a few key indicators used to assess a company’s financial leverage and risk exposure.

Beyond Taxes — The Real-World Cost of Debt

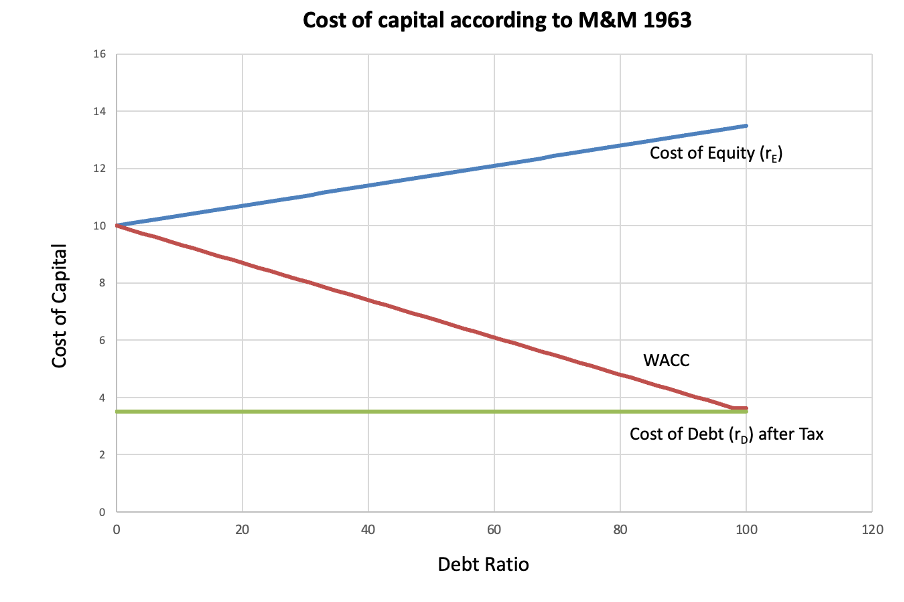
Capital structure theory begins with Modigliani and Miller (1958), who argued that in a perfect market—with no taxes or distress costs—a firm’s value is unaffected by its mix of debt and equity. This implies that financing decisions are irrelevant: the firm’s cost of capital remains unchanged regardless of leverage.

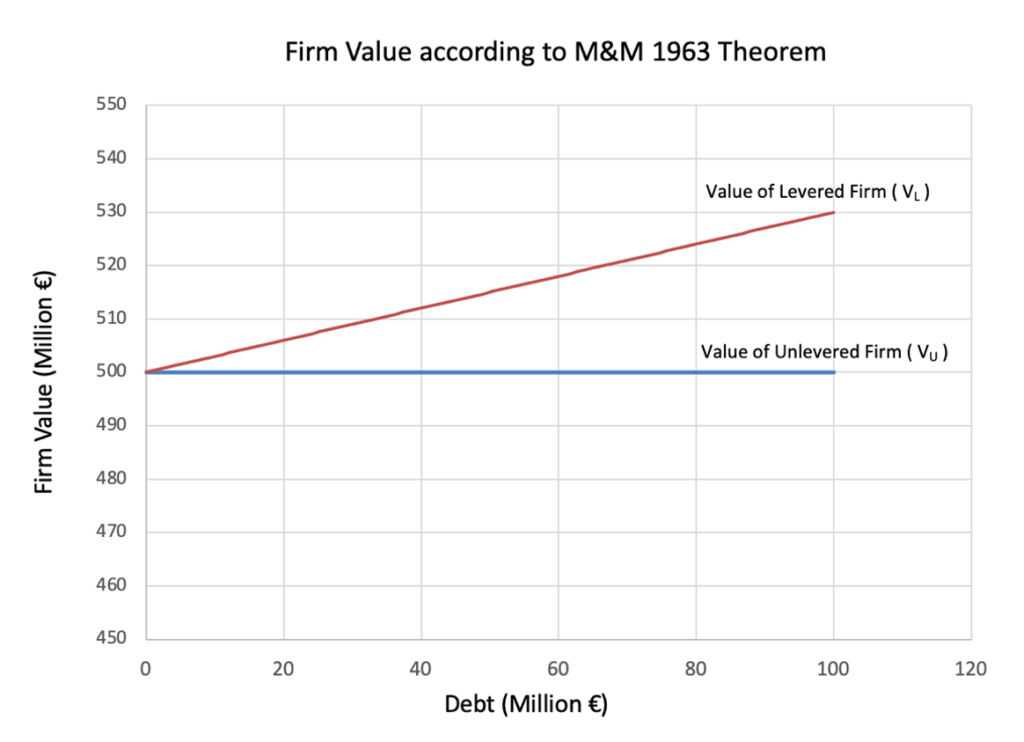
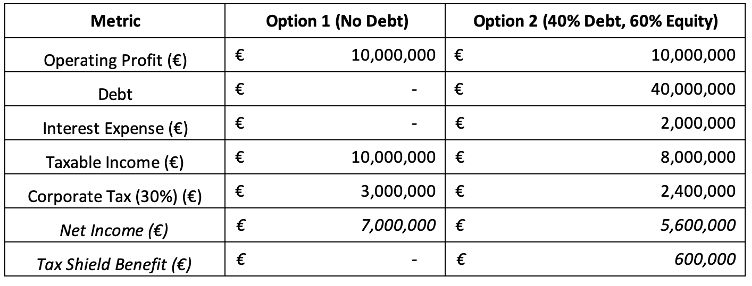
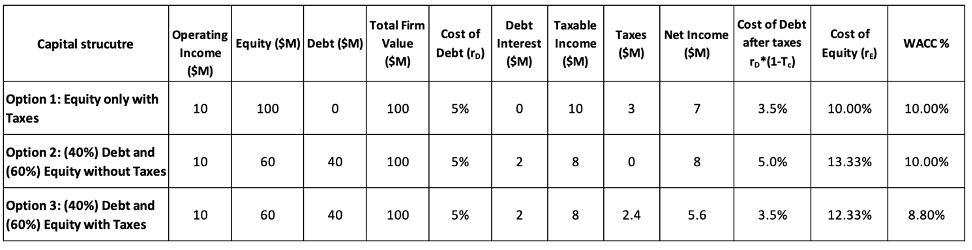
Their later work in 1963 introduced corporate taxes, shifting the narrative. Since interest is tax-deductible, debt creates a tax shield that reduces taxable income, lowering the firm’s WACC and increasing its value. In theory, this would mean the more debt a firm uses, the better.

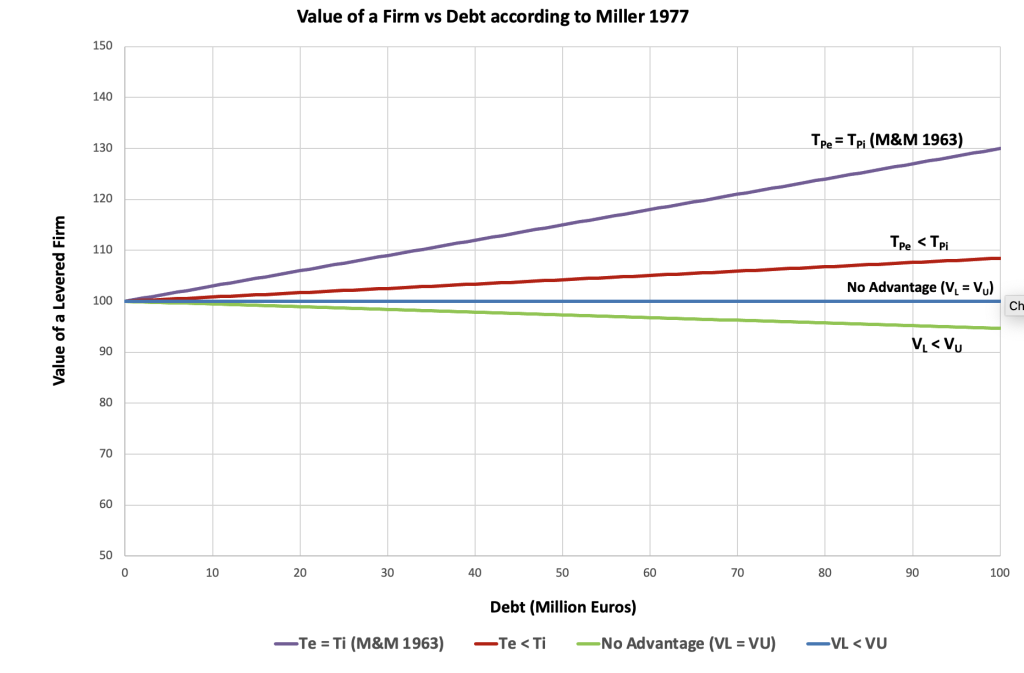
However, this doesn’t match real-world behaviour. Firms rarely use excessive debt. To explain this, Miller (1977) brought personal taxes into the picture. While firms benefit from interest deductibility, investors may face higher taxes on interest income compared to equity income. This reduces the net benefit of debt. At the market level, an equilibrium emerges where additional debt offers no further advantage—explaining why firms stop before 100% leverage.

Together, M&M and Miller show why debt can be attractive due to tax savings—but they don’t account for the costs of debt, which are crucial in practice. This article now turns to academic perspectives that build on these theories by introducing bankruptcy costs, financial distress, and agency issues, offering a more complete view of how firms decide on an optimal capital structure.

The Trade-Off Theory: Balancing Tax Shields and Bankruptcy Costs

While M&M (1963) and Miller (1977) emphasize the tax advantages of debt, real-world firms don’t pursue unlimited leverage. Why? Because with higher debt comes higher financial risk. This leads to the Trade-Off Theory—a more realistic and widely taught framework in modern corporate finance.

At the heart of this theory lies a simple question: How much debt is too much?

The Trade-Off Theory proposes that firms weigh the benefits of debt (primarily the interest tax shield) against the costs of debt (most notably bankruptcy risk and financial distress costs). The optimal capital structure is achieved when the marginal benefit of taking on more debt equals its marginal cost. Therefore, firms pick capital structure by trading off the benefits of the tax shield from debt against the costs of financial distress (including agency costs of debt).

This framework leads to a simple but powerful relationship:

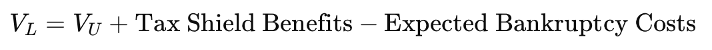
where:

  • VL is the value of a levered firm using debt.

  • VU is the value of a unlevered firm not using debt but only equity

  • Tax shield benefits: arising from the tax deductibility of interest payments

  • Expected bankruptcy cost: a function of both the probability of distress and the magnitude of associated losses (probability of distress x cost if distress occurs)

The Trade-Off Theory argues that the value of a firm initially increases with debt due to tax savings from interest deductibility, but only up to a point. Beyond that, the probability of bankruptcy and the costs associated with financial distress begin to outweigh the benefits of the tax shield. Due to this, there exists an optimal capital structure where the marginal benefit of debt exactly equals its marginal cost.

Tax shield benefit: This term represents the annual tax saving due to deductible interest.

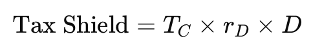
where:

  • TC: Corporate tax rate

  • rD: Interest rate on debt

  • D is the amount of debt of the firm

Expected Bankruptcy Cost:

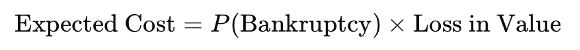
This cost includes:

  • Direct costs (legal, administrative): typically 2–5% of firm value

  • Indirect costs (reputation, supplier reactions, customer attrition): potentially far higher

How Firm Value Changes with Debt

According to the Trade-off Theory, the total value of a levered firm equals the value of the firm without leverage plus the present value of the expected tax savings from debt, less the present value of the expected financial distress costs.

It is represented as follows:

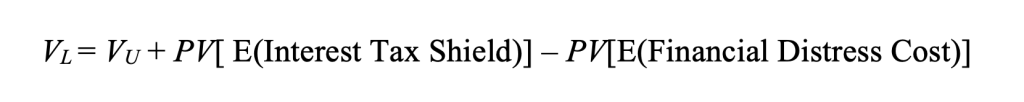
where:

  • VL is the value of a levered firm using debt.

  • VU is the value of a unlevered firm not using debt but only equity

Firms should increase leverage until they reach the optimal level where the firm value (and the net benefit of debt) is maximized. At the optimal leverage, the marginal benefits of interest tax shields that result from increasing leverage are perfectly offset by the marginal costs of financial distress.

Figure 1 – Trade-Off Theory Optimal Leverage

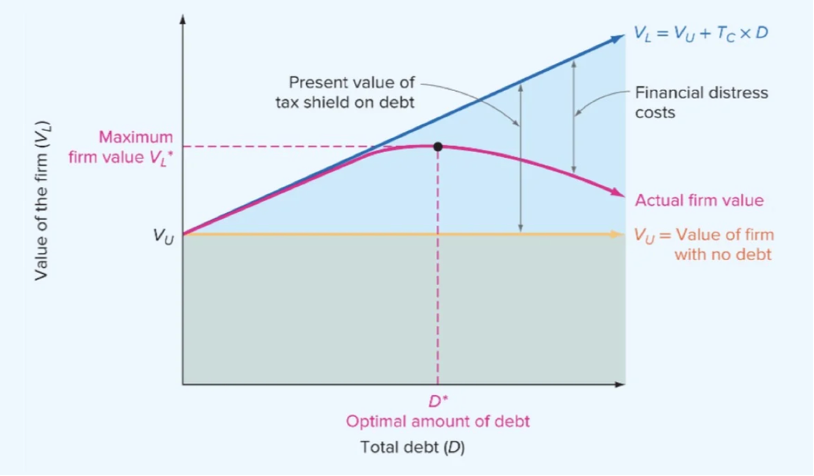
Source: “The Static Theory of Capital Structure” Brealey, Myers, & Allen

Figure 1 above illustrates the Trade-Off Theory of capital structure, which posits that a firm’s value is influenced by two opposing forces: the benefits of debt and the costs of financial distress.

  • The upward-sloping blue line represents the firm’s value if we consider only the corporate tax advantage of debt, where each additional unit of debt increases firm value by the present value of the tax shield (Tc×D). However, this idealized trajectory (as per M&M 1963) does not account for real-world frictions.

  • As leverage rises, so too does the probability of financial distress, bringing with it both direct costs (legal and administrative expenses) and indirect costs (reputation damage, lost sales, supplier concerns). These rising costs are reflected by the gap between the blue and pink curves.

  • The pink curve represents the actual value of a levered firm after subtracting distress costs. It shows the actual value of the firm once these financial distress costs are taken into account. Initially, this curve rises along with the tax shield benefits. But after a certain point, the marginal cost of debt begins to exceed its marginal benefit, causing the curve to flatten and then decline.

  • The pink curve peaks at the point marked D∗—the firm’s optimal capital structure. The point D∗ is the optimal amount of debt where the marginal benefit of the tax shield is exactly offset by the marginal expected cost of financial distress.

  • To the left of D∗, adding more debt increases firm value; to the right of it, further leverage diminishes value. The curve therefore reflects a concave relationship between debt and firm value, with the maximum point corresponding to the firm’s optimal capital structure.

Figure 1 delivers three core insights:

  • Leverage is a double-edged sword—it creates value through tax savings but erodes it through risk.

  • The optimal debt level is not universal—it depends on a firm’s industry, asset type, cash flow stability, and access to capital markets.

  • Real-world capital structure decisions are about finding a balance, not maximizing one benefit in isolation.

Static vs. Dynamic Trade-Off Models: From Simplified Theory to Real-World Complexity

The traditional Trade-Off Theory provides a powerful intuition: firms balance the benefits of debt (tax shields) against its costs (financial distress). However, how firms actually make capital structure decisions over time is more complex than the simple static view. This brings us to an important academic distinction: static vs. dynamic trade-off models.

Static Trade-Off Models: A Snapshot of Capital Structure

A static trade-off model is a one-period, one-time optimization framework. It assumes that a firm evaluates all its financing options at a single point in time and selects the capital structure that maximizes firm value. The firm is thought to instantly move to its optimal leverage ratio and maintain it indefinitely.

This model gives us a clean formula for firm value:

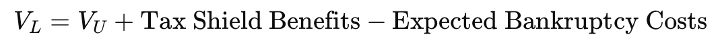
While this is helpful in teaching and early analysis, it oversimplifies real-world decision-making. Firms don’t reset their debt every day based on a formula. Instead, they must plan, adjust, and adapt—which is where dynamic models offer deeper insight.

Dynamic Trade-Off Models: Capturing Real-World Decision-Making

Dynamic trade-off models build on the static framework by recognizing that:

Capital structure is adjusted over time, not all at once. Firms face adjustment costs when issuing new debt or equity (e.g., flotation costs, signaling effects).

Business conditions, tax environments, interest rates, and risk evolve. Managers are forward-looking—they consider not only current benefits and costs but also future risks, taxes, and financing needs.

In these models, the optimal debt level is not a fixed point. Instead, firms operate within a target range of leverage and make gradual adjustments toward it when the benefits outweigh the costs of doing so.

For example:

A firm may not issue new debt today even if it’s slightly under-leveraged, because issuing comes with costs. It might instead wait for a better interest rate, a tax law change, or an internal cash flow event.

Dynamic models are particularly well-captured in the work of:

  • Fischer, Heinkel, and Zechner (1989) – who modelled how firms behave in a stochastic environment where recapitalization is costly.

  • Leland (1994) – who showed that default thresholds and optimal leverage depend on firm value and volatility over time.

Types of Bankruptcy Costs: The Hidden Burden of Excessive Leverage

While tax benefits of debt are quantifiable and immediate, the costs of financial distress—especially bankruptcy—are more nuanced, less visible, and often underestimated. These costs are central to the Trade-Off Theory, and understanding their components is essential for evaluating real-world capital structures.

Bankruptcy costs can be broadly classified into three types:

1. Direct Bankruptcy Costs

These are the explicit, out-of-pocket expenses incurred during legal bankruptcy proceedings.

  • Legal fees, court costs, bankruptcy consultants

  • Administrative expenses, such as auditing and trustee services

Empirical studies suggest that direct costs range from 2–5% of firm value, though they may be higher in complex bankruptcies. While these are easier to measure, they are not necessarily the largest component.

Example: A manufacturing firm with a $500 million valuation that enters Chapter 11 could incur $10–25 million in legal and court-related costs alone.

2. Indirect Bankruptcy Costs

These are opportunity costs or value losses incurred even if bankruptcy does not occur—simply being in distress can harm the business.

  • Loss of customers: Buyers lose trust in a distressed brand.

  • Supplier tightening: Suppliers demand advance payments or withdraw credit.

  • Employee turnover: Top talent exits due to job insecurity.

  • Delayed investments: Management focuses on liquidity over strategy.

Indirect costs are often much larger than direct ones—estimated at 10–20% of firm value in some studies.

Example: A hotel chain facing debt pressure may see a fall in bookings, reduced vendor support, and higher staff attrition—impacting operations even before legal proceedings begin.

3. Agency Costs of Debt

As financial distress increases, so do agency conflicts between debt holders and equity holders.

Two prominent issues are:

  • Asset Substitution Problem – Shareholders may prefer riskier projects with higher upside (but higher default risk) because they capture the gains, while losses are partially borne by creditors.

  • Underinvestment Problem – Highly leveraged firms might pass on positive NPV projects because the gains would go to debt holders, not shareholders. Thus, debt discourages investment when it is most needed.

These agency costs distort management incentives, especially when firms are close to violating debt covenants or already under pressure.

Academic Contributions on Bankruptcy and Alternative Views on Capital Structure

Pecking Order Theory and Information Asymmetry

Contrasting the Trade-Off Theory, Myers and Majluf (1984) introduced the Pecking Order Theory, which prioritizes financing sources based on information asymmetry. Firms prefer internal financing (retained earnings) first, then debt, and issue equity only as a last resort. This hierarchy arises because managers possess more information about the firm’s value than external investors, leading to adverse selection concerns when issuing new equity.

Dynamic Models of Capital Structure

Recognizing that capital structure decisions are not static, researchers have developed dynamic models to reflect real-world complexities. Leland (1994) incorporated factors such as agency costs, taxes, and bankruptcy costs into a continuous-time framework, providing insights into how firms adjust their leverage over time in response to changing conditions.

Human Capital and Bankruptcy Risk

Recent studies have explored the interplay between human capital and capital structure. For instance, research by Berk, Stanton, and Zechner (2010) examines how firms with significant human capital considerations may adopt lower leverage to mitigate the adverse effects of financial distress on their workforce and overall operations.

Empirical Evidence and Contemporary Reviews

Empirical studies have tested these theories across various contexts. For example, research published in the Journal of Finance investigates how bankruptcy risk influences firms’ capital structure choices, revealing an inverse relationship between bankruptcy risk and leverage. Comprehensive literature reviews, such as those by Cerkovskis et al. (2022) and Visinescu and Micuda (2023), provide critical analyses of the evolution and empirical validation of capital structure theories, offering valuable insights for both scholars and practitioners.

Practical Considerations in Capital Structure Decisions

While theories like Modigliani-Miller (M&M), the Trade-Off Theory, and Agency Cost Theory provide useful frameworks for understanding capital structure, real-world evidence shows that firms consider multiple factors beyond theory when making financing decisions. Empirical studies highlight how industries, economic conditions, credit ratings, and market perceptions influence a company’s choice between debt and equity.

Real-World Capital Structure Choices

Empirical research supports the idea that firms do not strictly follow any single capital structure theory but instead balance tax advantages, financial flexibility, and risk. Some key observations from real-world studies include:

  • Myers (1984) found that firms follow a “Pecking Order” when raising funds, preferring internal financing (retained earnings) first, followed by debt, and issuing equity as a last resort due to information asymmetry.

  • Graham (2000) estimated that firms use only about 60% of the potential tax benefits of debt, indicating that firms hesitate to take on excessive leverage due to bankruptcy risks.

  • Frank & Goyal (2009) confirmed that larger, more profitable firms tend to have higher leverage, while smaller, riskier firms avoid debt due to financial distress concerns.

These studies suggest that firms do not maximize leverage, but rather choose a debt level that balances benefits and risks based on firm size, profitability, and market conditions.

Why Should I Be Interested in This Post?

Understanding a firm’s optimal debt structure is essential for anyone involved in finance, strategy, or investment analysis. Whether you’re an investor evaluating risk, a finance professional shaping capital decisions, or a student building foundational knowledge, the trade-off between debt and equity lies at the core of corporate financial strategy. This post offers a deep dive into the academic perspectives on capital structure, highlighting how bankruptcy costs, financial distress, and tax considerations influence real-world financing decisions. By mastering these concepts, you’ll be better equipped to assess firm value, understand risk-return dynamics, and make more informed financial judgments in a world where leverage can both create and destroy value.

Related posts on the SimTrade blog

   ▶ Snehasish CHINARA Optimal capital structure with corporate and personal taxes: Miller 1977

   ▶ Snehasish CHINARA Optimal capital structure with taxes: Modigliani and Miller 1963

   ▶ Snehasish CHINARA Optimal capital structure with no taxes: Modigliani and Miller 1958

   ▶ Snehasish CHINARA Solvency and Insolvency in the Corporate World

   ▶ Snehasish CHINARA Illiquidity, Liquidity and Illiquidity in the Corporate World

   ▶ Snehasish CHINARA Illiquidity, Solvency & Insolvency : A Link to Bankruptcy Procedures

   ▶ Snehasish CHINARA Chapter 7 vs Chapter 11 Bankruptcies: Insights on the Distinction between Liquidations & Reorganisations

   ▶ Snehasish CHINARA Chapter 7 Bankruptcies: A Strategic Insight on Liquidations

   ▶ Snehasish CHINARA Chapter 11 Bankruptcies: A Strategic Insight on Reorganisations

   ▶ Akshit GUPTA The bankruptcy of Lehman Brothers (2008)

   ▶ Akshit GUPTA The bankruptcy of the Barings Bank (1996)

   ▶ Anant JAIN Understanding Debt Ratio & Its Impact On Company Valuation

Useful resources

US Courts Data – Bankruptcy

S&P Global – Bankruptcy Stats

Statista – Bankruptcy data

About the author

The article was written in July 2025 by Snehasish CHINARA (ESSEC Business School, Grande Ecole Program – Master in Management, 2022-2025).

Optimal capital structure with corporate and personal taxes: Miller 1977 

by
Snehasish CHINARA

In this article, Snehasish CHINARA (ESSEC Business School, Grande Ecole Program – Master in Management, 2022-2025) explores the optimal capital structure for firms, which refers to the balance between debt and equity financing. This post focuses on how the impact of personal taxes on the firm capital structure. The author unpacks Miller’s 1977 proposition, which presents a formula for calculating the right tax advantage of debt, and explains how it helps reconcile theory with what we actually observe in practice.

Introduction

When Modigliani and Miller introduced their capital structure theory in 1958, they shook the foundations of corporate finance. They argued that, in a perfect market with no taxes, no bankruptcy costs, and no frictions, a firm’s value is completely independent of how it is financed. In other words, it doesn’t matter whether a firm uses debt, equity, or a combination of both—the total firm value remains the same.

In 1963, Modigliani and Miller revised their theory to incorporate corporate taxes. With this adjustment, interest payments on debt are tax-deductible, and then provide firms with a “tax shield” that effectively reduces the cost of debt. This made debt financing more attractive than equity, leading to the conclusion that firms should increase their leverage to maximize their value (ideally reaching a 100 debt ratio). In the extreme, this version of the theory suggested that firms should be financed entirely with debt to benefit from the maximum tax advantage.

However, the real world tells a different story. Very few firms rely solely on debt. In fact, most maintain a balanced mix of debt and equity. If debt is supposedly so advantageous under corporate tax rules, why don’t we see more of it being used? This is where Merton Miller’s 1977 work offers a crucial refinement to the theory.

Miller introduced a critical yet often overlooked component into the capital structure discussion: personal taxes. While interest payments are tax-deductible at the corporate level, the income received by investors—whether as interest or dividends—is also subject to personal taxation. Importantly, interest income is often taxed at a higher rate than equity income (like capital gains or dividends). This means the supposed advantage of debt at the corporate level may be offset—or even completely nullified—by the higher tax burden borne by investors.

Modigliani-Miller 1963 Theorem (M&M 1963)

Let us first remind you about the main findings of Modigliani and Miller (1963). In their revision of their first article published a few years earlier (1958), their theory about the firm capital structure introduced corporate taxes, which has a crucial impact on their earlier conclusions which found that the capital structure was irrelevant. They recognized that, in most economies, governments impose corporate income tax, but companies can deduct interest payments on debt from their taxable income. This interest tax-shield increases the after-tax profits of a firm and thereby raises its overall value.

The tax shield refers to the reduction in taxable income that results from interest payments on debt. Since interest expenses are tax-deductible, they effectively reduce the amount of taxes a company owes. This provides a direct financial benefit to firms that use debt financing, making it a valuable tool for optimizing capital structure.

The formula for the tax shield is:

This means that, under the M&M (1963) proposition, the value of a leveraged firm is given by:

where:

  • VL is the value of a levered firm using debt.

  • VU is the value of a unlevered firm not using debt but only equity

  • Tc is the Corporate tax rate

  • D is the amount of debt of the firm

This formula shows that the value of a firm increases by the amount of tax shield (Tc⋅D) when debt is introduced into the capital structure. The more debt a company takes on, the greater the tax benefit, making debt financing more attractive than equity financing.

Miller (1977): The Role of Personal Taxes in Capital Structure

Modigliani and Miller’s 1963 revision made a powerful case for debt: because interest payments are tax-deductible, firms enjoy a tax shield that reduces their cost of capital. The logical (but extreme) implication of this idea was that firms should maximize debt in their capital structure. However, the theory still fell short of explaining reality—most firms do not load up on debt. Why?

This is where Merton Miller’s 1977 paper brought a major refinement. While M&M (1963) focused on corporate taxes, Miller highlighted the crucial role of personal taxes paid by investors. Specifically, he noted that:

  • Interest income (from bonds or loans) is typically taxed at a higher personal rate (TPi),

  • While equity income (via dividends or capital gains) is often taxed at a lower rate (TPe).

Thus, although the firm saves taxes through debt, the investor receiving interest income may lose part of that advantage due to higher personal taxes. Miller argued that the tax benefit of debt is not universal—it depends on the relative tax positions of the firm and its investors.

Miller quantified the net tax advantage of debt with the following formula:

where:

  • TPi is the personal tax rate on interest income

  • TPe is the personal tax rate on equity income (dividends/capital gains)

  • Tc is the corporate tax rate

This expression compares the after-tax returns from debt and equity financing, from both the firm’s and investor’s perspectives.

Value of a Levered Firm according to Miller (1977)

In Miller (1977), the value of the firm incorporates both:

1. The corporate tax shield (from M&M 1963), and

2. The personal tax disadvantage from investor taxation on interest income.

Unlike M&M 1963 (which assumed value keeps increasing with leverage due to tax shields), Miller showed that the firm’s value plateaus at an equilibrium level, reflecting the offsetting effect of personal taxes.

There isn’t a single formula as elegant as in M&M 1963 because Miller focuses on market equilibrium, not firm-level maximization. But we can express the adjusted value of a levered firm relative to the unlevered firm as:

that is,

where:

  • VL is the value of a levered firm using debt.

  • VU is the value of a unlevered firm not using debt but only equity

  • Tc is the Corporate tax rate

  • TPi is the personal tax rate on interest income

  • TPe is the personal tax rate on equity income (dividends/capital gains)

  • D is the amount of debt of the firm

Figure 1. Firm Value vs Debt according to Miller 1977 Theorem

where:

  • Tc is the Corporate tax rate

  • TPi is the personal tax rate on interest income

  • TPe is the personal tax rate on equity income (dividends/capital gains)

The Equilibrium Capital Structure Across Firms

One of the most insightful—and often misunderstood—contributions of Miller (1977) is that there is no single “optimal” capital structure for all firms. Instead of recommending that every company should maximize debt (as M&M 1963 might suggest), Miller argued that the optimal mix of debt and equity depends on the broader market, not just individual firm decisions. His approach introduced a market-level equilibrium perspective, which helps us understand the diverse financing strategies we observe in the real world.

Miller recognized that not all investors are taxed equally. Some investors—like pension funds, endowments, or individuals in low tax brackets—are less affected by taxes on interest income. These investors prefer debt because they can earn stable interest income without facing significant tax penalties. On the other hand, investors in higher tax brackets might favour equity, particularly because capital gains and dividends are often taxed at lower rates than interest income.

This diversity in investor preferences (from different personal tax rates) creates a kind of natural balance in the financial markets. Some firms will issue more debt to attract income-focused investors, while others will rely more on equity to appeal to investors who value capital gains. Over time, this leads to a market equilibrium in which different firms adopt different capital structures based on the preferences of the investors they attract.

In reality, we do not see all firms aggressively using debt to lower their tax bills. Instead, we see some firms—like utilities or financial institutions—using higher levels of debt, while others—like tech startups or growth firms—rely more on equity. This variation observed in practice aligns perfectly with Miller’s theory. The aggregate tax advantage of debt is “used up” across the economy, so not every firm needs to (or should) leverage itself heavily.

Firms essentially compete for investor types, and their capital structure decisions reflect the marginal investor’s personal tax situation. In this way, the equilibrium is not found at the level of a single firm, but across the entire set of firms.

How Miller (1977) Redefined the Cost of Equity and WACC from Modigliani-Miller (1963)

In M&M (1963), the introduction of corporate taxes led to a crucial insight: because interest payments are tax-deductible, debt financing creates a tax shield that reduces the firm’s Weighted Average Cost of Capital (WACC). The model predicted that, as leverage increases, WACC decreases, and firm value rises—implying that a firm should use as much debt as possible to minimize its cost of capital.

This had a direct impact on the cost of equity as well. In M&M (1963), the cost of equity (rE) increases with leverage to compensate for the rising risk faced by shareholders:

where:

  • rE is the cost of equity for a levered firm

  • rU is the cost of equity for an unlevered firm

  • rD is the cost of debt

  • D/E is the debt to equity ratio measuring leverage

Here, while the cost of equity increases due to higher financial risk, the overall WACC falls, thanks to the tax shield:

Where: V is the Value of the firm (V= D + E)

Miller (1977) introduced personal taxes into the equation—something that M&M (1963) completely ignored. He observed that investors are not only taxed at the corporate level but also at the personal level:

  • Interest income is taxed at the personal level (personal tax rate on interest income: TPi)

  • Equity dividends and capital gains are taxed at the personal level (personal tax rate on equity: TPe)

Crucially, interest income is taxed more heavily than equity dividends and capital gains: TPi > TPe. This is the case in the United States and most developed countries.

This alters the perceived tax advantage of debt as the benefit of corporate tax deductibility may be neutralized—or even outweighed—by the higher taxes on interest income.

While Miller (1977) didn’t give a neatly adjusted cost of equity formula like Modigliani and Miller (1963), he did show that the tax advantage of debt financing is not universal—it depends on both corporate and personal tax rates. This led to a redefinition of the net tax advantage of debt, which in turn affects WACC:

And so, the adjusted value of the tax shield, and by extension the impact of debt on WACC, becomes:

Using this expression, the WACC becomes:

where,

  • Tc is the Corporate tax rate

  • TPi is the personal tax rate on interest income

  • TPe is the personal tax rate on equity income (dividends/capital gains)

  • D/V is the proportion of debt in the capital structure

  • E/V is the Proportion of equity in the capital structure

  • rE is the cost of equity for a levered firm

  • rD is the cost of debt

This means that the WACC no longer declines indefinitely with debt. Instead, as the tax burden on interest income increases (via Ti ), the marginal benefit of debt diminishes. At market equilibrium, the advantage of debt disappears, and WACC flattens—explaining why we observe moderate, not extreme, debt usage in practice.

  • If Ti > Te and corporate tax Tc is high, debt still offers a net tax advantage, though smaller than in M&M (1963).

  • If the term in brackets equals zero, there is no net tax advantage—WACC remains flat regardless of leverage.

  • If the term becomes negative, equity becomes more tax-efficient, and adding debt raises the WACC.

Why Should I Be Interested in This Post?

In corporate finance, the debate around how much debt a firm should take on is far from settled. While traditional models like Modigliani-Miller (1963) emphasize the tax benefits of debt, they ignore the taxes investors pay. This post introduces the groundbreaking Miller (1977) framework, which shows how personal taxes can offset corporate tax advantages, reshaping our understanding of optimal capital structure. If you’re a finance student, investor, or aspiring professional, understanding this equilibrium-based view will give you a more realistic—and nuanced—perspective on how real-world firms decide between debt and equity.

Related posts on the SimTrade blog

   ▶ Snehasish CHINARA Optimal capital structure with taxes: Modigliani and Miller 1963

   ▶ Snehasish CHINARA Optimal capital structure with no taxes: Modigliani and Miller 1958

   ▶ Snehasish CHINARA Solvency and Insolvency in the Corporate World

   ▶ Snehasish CHINARA Illiquidity, Liquidity and Illiquidity in the Corporate World

   ▶ Snehasish CHINARA Illiquidity, Solvency & Insolvency : A Link to Bankruptcy Procedures

   ▶ Snehasish CHINARA Chapter 7 vs Chapter 11 Bankruptcies: Insights on the Distinction between Liquidations & Reorganisations

   ▶ Snehasish CHINARA Chapter 7 Bankruptcies: A Strategic Insight on Liquidations

   ▶ Snehasish CHINARA Chapter 11 Bankruptcies: A Strategic Insight on Reorganisations

   ▶ Akshit GUPTA The bankruptcy of Lehman Brothers (2008)

   ▶ Akshit GUPTA The bankruptcy of the Barings Bank (1996)

   ▶ Anant JAIN Understanding Debt Ratio & Its Impact On Company Valuation

Useful resources

US Courts Data – Bankruptcy

S&P Global – Bankruptcy Stats

Statista – Bankruptcy data

About the author

The article was written in July 2025 by Snehasish CHINARA (ESSEC Business School, Grande Ecole Program – Master in Management, 2022-2025).

Optimal capital structure with taxes: Modigliani and Miller 1963

by
Snehasish CHINARA

In this article, Snehasish CHINARA (ESSEC Business School, Grande Ecole Program – Master in Management, 2022-2025) explores the optimal capital structure for firms, which refers to the balance between debt and equity financing. This post dives into the article written by Modigliani and Miller (1963) which explores the case of corporate tax and a frictionless market (no bankruptcy costs).

Introduction to Modigliani and Miller Propositions

In 1958, Franco Modigliani and Merton Miller introduced a groundbreaking theory on capital structure, famously known as the M&M Proposition. Their research concluded that, under certain ideal conditions, the way a company finances itself—whether through debt or equity—does not affect its overall value. This result, known as the Capital Structure Irrelevance Principle, was based on assumptions such as no corporate taxes, no bankruptcy costs, and perfect capital markets. The intuition behind this idea is simple: if investors can create their own leverage by borrowing personally at the same rate as firms, then a company’s financing mix should not matter for its value.

According to M&M Proposition I (1958), in a frictionless world:

where:

  • VL is the value of a levered firm using debt.

  • VU is the value of a unlevered firm not using debt but only equity

Key Assumptions:

  • No taxes (in reality, firms pay corporate taxes).

  • No bankruptcy costs (in reality, firms pay costs if they go bankrupt).

  • No financial distress (in reality, too much debt can make investors nervous).

However, this initial model had a major limitation: it ignored the effect of corporate taxes. In reality, most governments tax corporate profits, but they allow firms to deduct interest expenses on debt from taxable income. This means that using debt provides a tax advantage, which was missing from the 1958 model. Recognizing this, Modigliani and Miller revised their original work in 1963, introducing the impact of corporate taxes. Their new findings dramatically changed the conclusion: debt financing increases firm value because interest payments reduce taxable income, creating a tax shield. This update laid the foundation for modern corporate finance by showing that, with corporate taxes, firms should prefer debt over equity.

Modigliani-Miller 1963 Theorem (M&M 1963)

Modigliani and Miller’s 1963 revision to their capital structure theory introduced the concept of corporate taxes, which has a crucial impact on their earlier conclusions. They recognized that, in most economies, governments impose corporate income tax, but companies can deduct interest payments on debt from their taxable income. This interest tax-shield increases the after-tax profits of a firm and thereby raises its overall value.

The tax shield refers to the reduction in taxable income that results from interest payments on debt. Since interest expenses are tax-deductible, they effectively reduce the amount of taxes a company owes. This provides a direct financial benefit to firms that use debt financing, making it a valuable tool for optimizing capital structure.

The formula for the tax shield is:

Since interest expense is calculated as:

Therefore, the tax shield for a single year becomes:

The Modigliani-Miller (1963) model assumes perpetual debt primarily for simplification and mathematical clarity. The use of perpetual debt helps in calculating the present value of the tax shield without the need for complex discounting over a finite period.

If the firm has perpetual debt, meaning it never repays the principal and continues paying interest forever, the total value of the tax shield is found by calculating the present value of all future tax shield benefits. Since the tax shield is received every year indefinitely, its present value is:

Using the cost of debt (rd) as the discount rate, we get:

The (rd) cancels out, simplifying to:

This means that, under the M&M (1963) proposition, the value of a leveraged firm is given by:

where:

  • VL is the value of a levered firm using debt.

  • VU is the value of a unlevered firm not using debt but only equity

  • Tc is the Corporate tax rate

  • D is the amount of debt of the firm

This formula shows that the value of a firm increases by the amount of tax shield (Tc⋅D) when debt is introduced into the capital structure. The more debt a company takes on, the greater the tax benefit, making debt financing more attractive than equity financing.

Figure 1. Firm Value vs Debt according to M&M 1963 Theorem

In simple terms, taxes make debt financing more beneficial because firms pay interest on debt before paying taxes, reducing their taxable income. On the other hand, dividends paid to equity shareholders are not tax-deductible, meaning that firms must pay taxes on their entire profit before distributing dividends.

Implication for Capital Structure Decisions:

Firms benefit from using debt due to the tax shield, leading to a preference for more leverage.

The Modigliani-Miller (1963) model with taxes suggests that because of the tax shield on debt, a firm’s value increases as it takes on more debt. The formula for value of a levered firm according to M&M(1963) shows that every additional unit of debt directly increases firm value by the tax savings it provides. In theory, this means that a firm should finance itself entirely with debt (100% debt financing) to maximize its value. This is a significant departure from M&M (1958), where capital structure had no effect on firm value.

Limitations

However, in real-world scenarios, firms do not rely solely on debt. This is because excessive debt increases the risk of financial distress and bankruptcy costs, which M&M (1963) did not initially consider.

Case Study: Implications of M&M 1963 (Optimal Capital Structure with corporate taxes)

Alpha Corp operates in an imperfect capital market (with taxes only). It has two financing options for the capital structure:

  • Option 1: equity only (100% equity, 0% debt)

  • Option 2: debt and equity (60% equity, 40% debt)

Each option funds a $100 million investment that generates an annual operating income of $10 million. The risk-free interest rate is 5%, and the corporate tax rate is 30%.

Figure 2. Simplified Balance Sheet of Alpha Corp

Table 1. M&M 1963: an Example

Based on Table 1, the key takeaways are as follows:

1.Debt Creates a Tax Shield:

  • Under Option 2 (40% debt, 60% equity), Alpha Corp pays €2 million in interest expense, reducing taxable income from €10 million to €8 million.

  • This results in a lower corporate tax payment (€2.4 million instead of €3 million), leading to a €600,000 tax shield benefit.

2.Net Income is Lower with Debt, But Firm Value Increases:

  • Despite reducing tax liability, net income under Option 2 (€5.6 million) is lower than Option 1 (€7 million) because of interest expenses.

  • However, the firm’s total value increases due to the tax shield, meaning equity holders still benefit from debt financing.

How Modigliani-Miller (1963) Redefined the Cost of Equity and WACC from Modigliani-Miller (1958)

In Modigliani-Miller (1958), the firm’s capital structure—the mix of debt and equity—was considered irrelevant to its overall cost of capital (WACC) and, by extension, its firm value. This proposition, based on ideal market conditions (no taxes, no bankruptcy costs), argued that whether a firm is financed by debt or equity, the overall cost of capital remains unchanged. The cost of equity increases with leverage because equity holders demand higher returns to compensate for the additional financial risk, but this increase in cost of equity was offset by the lower cost of debt. Therefore, WACC stayed constant regardless of a firm’s capital structure.

However, when Modigliani and Miller (1963) introduced corporate taxes into their model, they demonstrated a significant change in the cost of capital (WACC) and cost of equity dynamics. With the tax deductibility of interest payments on debt, the cost of debt is effectively reduced, which leads to a reduction in WACC. This creates a clear benefit for firms that use more debt in their capital structure, making debt financing a value-enhancing tool. Let’s explore these key differences in detail.

Impact on the Cost of Equity (rE)

MM (1958) – Cost of Equity Increases with Leverage

Under the Modigliani-Miller (1958) framework, the cost of equity (rE) increases as a firm takes on more debt because equity holders demand higher returns for taking on additional risk due to leverage. The relationship between cost of equity and leverage is described by the following formula:

where:

  • rE is the cost of equity for a levered firm

  • rU is the cost of equity for an unlevered firm

  • rD is the cost of debt

  • D/E is the debt to equity ratio measuring leverage

This formula shows that as a firm increases its debt, its cost of equity increases to compensate for the increased financial risk borne by equity holders. However, since debt is cheaper than equity, the overall WACC remains unchanged.

MM (1963) – Tax Shield Reduces the Impact on Cost of Equity In MM (1963), the introduction of corporate taxes changes the scenario. Since interest expenses on debt are tax-deductible, the effective cost of debt (rD) becomes lower. This reduces the overall risk for the firm and, therefore, the increase in the cost of equity (rE) is less severe than in MM (1958). The new formula for cost of equity becomes:
where Tc is the corporate tax rate. The (1 – Tc) term reduces the increase in cost of equity (rE), because the firm’s debt is now partially subsidized by the tax shield. This shows that while leverage still increases the cost of equity (rE), the effect is less pronounced in the presence of tax deductibility of interest payments.

Impact on the Weighted Average Cost of Capital (WACC)

M&M (1958) – WACC Remains Constant Regardless of Leverage

In MM (1958), because the increase in the cost of equity (rE) offsets the benefit of cheaper cost of debt (rD), the WACC remains constant no matter the debt-to-equity ratio. The formula for WACC in this model is:

where:

  • V=D+E is the total firm value

  • rE is the cost of equity for a levered firm

  • rD is the cost of debt

  • D is the total debt

  • E is the total equity

According to MM (1958), since debt and equity are in perfect balance (i.e., the increase in the cost of equity (rE) is offset by the lower cost of debt (rD)), the WACC stays constant. The capital structure—how much debt or equity a firm uses—has no effect on the overall cost of capital or the firm’s value in a world without taxes.

MM (1963) – WACC Declines as Debt Increases

With the introduction of taxes, MM (1963) shows that WACC decreases as a firm increases its debt. The tax shield created by the deductibility of interest payments lowers the effective cost of debt (rD), making debt financing more attractive.

The formula for after-tax WACC in MM (1963) is:

In this scenario, debt financing becomes more advantageous because the firm can lower its overall WACC by utilizing debt, which reduces the tax burden. The WACC decreases as a firm increases its leverage (debt) because the cost of debt (rD) is reduced due to the tax shield, and the cost of equity (rE) increases at a slower rate due to the reduced impact of debt on financial risk.

Figure 3. Modigliani-Miller View Of Gearing And WACC: With Taxation (MM 1963)

Case Study: Implications of M&M 1963 (Optimal Capital Structure with corporate taxes)

Alpha Corp operates in a capital market (no bankruptcy costs, and no market imperfections). It has two financing options:

  • Option 1: Fully equity-financed (No debt with Corporate Taxes of 30%)

  • Option 2: 40% Debt, 60% Equity (without Corporate Taxes)

  • Option 3: 40% Debt, 60% Equity (with Corporate Taxes of 30% )

Each option funds a $100 million investment that generates an annual operating income of $10 million. The risk-free interest rate is 5%, and the required return on equity is 10%.

Figure 4. Modigliani-Miller View Of Gearing And WACC: With Taxation (MM 1963)

Table 2. M&M 1963: an Example

Key takeaways from this example are as follows :

1. Corporate Taxes Make Debt Financing More Attractive by Reducing the Effective Cost of Debt

  • In a no-tax world (M&M 1958, Option 2), firms are indifferent between debt and equity, as capital structure does not affect WACC.

  • However, M&M (1963) proves that in a taxed environment (Option 3), debt financing creates value because interest payments reduce taxable income, leading to lower corporate taxes.

  • This is called the “tax shield” effect, where firms pay less in taxes by using debt, increasing after-tax cash flows available to shareholders.

2. WACC Declines with Leverage When Corporate Taxes Exist, Unlike in M&M (1958)

  • In M&M (1958) (no taxes, Option 2), WACC remains constant at 10%, regardless of leverage.

  • M&M (1963) (Option 3) introduces taxes, causing WACC to drop to 8.80% due to the tax shield.

  • Strategic Takeaway: Firms can reduce their cost of capital and increase firm value by incorporating moderate levels of debt into their capital structure.

3. Cost of Equity Increases with Debt, But the Tax Shield Reduces the Rate of Increase

  • Higher leverage increases financial risk for shareholders, leading to a higher required return on equity (rE).

  • In Option 2 (M&M 1958, No Taxes), introducing 40% debt raises the cost of equity to 13.33% due to added risk.

  • In Option 3 (M&M 1963, With Taxes), the cost of equity only increases to 12.33%, because the tax shield offsets part of the financial risk.

4. After-Tax Cost of Debt is Lower than the Cost of Equity, Making Debt a Cheaper Financing Option

  • The cost of debt before taxes is 5%.

  • Due to the corporate tax rate (30%), the effective cost of debt is reduced: rDafter-tax= rD ×(1−Tc)

  • Comparing Financing Costs in Option 3:

    • Cost of Equity (rE) = 12.33%

    • After-Tax Cost of Debt (rD) = 3.5%

  • Debt financing is significantly cheaper than equity financing after adjusting for the tax shield.

  • Firms should utilize debt strategically to lower overall financing costs.

5. The Trade-Off Between Tax Benefits and Financial Distress Risk Determines the Optimal Capital Structure

  • M&M (1963) suggests using more debt to reduce WACC, but in reality, excessive debt increases financial distress risks.

  • While debt reduces WACC through the tax shield, too much debt leads to higher bankruptcy risks, credit downgrades, and operational constraints.

  • Most firms balance debt and equity to optimize WACC, using debt to take advantage of tax savings without excessive financial risk.

Takeaways on Optimal Debt Structure and Bankruptcy Costs from M&M 1963 Theorem

The Modigliani-Miller (1963) proposition demonstrated that the presence of corporate taxes fundamentally changes the implications of capital structure on firm value. Unlike their earlier 1958 proposition, where capital structure was deemed irrelevant, the 1963 revision highlighted the benefits of debt financing due to the tax shield effect. Since interest expenses on debt are tax-deductible, firms can reduce their taxable income and, consequently, their tax obligations. This finding suggests that, in a world with corporate taxes and no other frictions, firms should finance themselves entirely with debt to maximize their value.

The M&M (1963) proposition remains a cornerstone in understanding capital structure decisions, demonstrating that debt financing enhances firm value through tax savings. However, in practice, firms must carefully balance leverage to avoid excessive financial distress. The optimal capital structure is not purely debt-driven but rather a carefully calibrated mix of debt and equity that maximizes firm value while maintaining financial stability.

Why Should I Be Interested in This Post?

This post explains a key concept in corporate finance—how debt financing affects firm value through corporate tax benefits and financial risks. If you’re a student, finance professional, or investor, understanding the Modigliani-Miller (1963) proposition will help you grasp why companies use debt. With clear explanations, real-world examples, and Excel-based analysis, this post provides practical insights into optimal capital structure decisions.

Related posts on the SimTrade blog

   ▶ Snehasish CHINARA Optimal capital structure with no taxes: Modigliani and Miller 1958

   ▶ Snehasish CHINARA Solvency and Insolvency in the Corporate World

   ▶ Snehasish CHINARA Illiquidity, Liquidity and Illiquidity in the Corporate World

   ▶ Snehasish CHINARA Illiquidity, Solvency & Insolvency : A Link to Bankruptcy Procedures

   ▶ Snehasish CHINARA Chapter 7 vs Chapter 11 Bankruptcies: Insights on the Distinction between Liquidations & Reorganisations

   ▶ Snehasish CHINARA Chapter 7 Bankruptcies: A Strategic Insight on Liquidations

   ▶ Snehasish CHINARA Chapter 11 Bankruptcies: A Strategic Insight on Reorganisations

   ▶ Akshit GUPTA The bankruptcy of Lehman Brothers (2008)

   ▶ Akshit GUPTA The bankruptcy of the Barings Bank (1996)

   ▶ Anant JAIN Understanding Debt Ratio & Its Impact On Company Valuation

Useful resources

US Courts Data – Bankruptcy

S&P Global – Bankruptcy Stats

Statista – Bankruptcy data

About the author

The article was written in January 2025 by Snehasish CHINARA (ESSEC Business School, Grande Ecole Program – Master in Management, 2022-2025).